Truss Spar平臺在船舶碰撞下的數值模擬分析

汪 宏，明杉杉，楊 浩，馮 森，徐同達，夏蘭強

(江蘇科技大學 船舶與海洋工程學院，江蘇 鎮江 212003)

0 引 言

Spar平臺在海洋開發中的應用已經超過30多年，但在1987之前其主要是作為輔助系統使用比如浮標、海洋科研站、海上通信中轉站等。Spar作為鉆井平臺主要有3種類型[1]：傳統Spar平臺（Classic Spar）、桁架式Spar平臺（Truss Spar）和多柱式Spar平臺（Cell Spar）。海洋平臺在復雜海域進行工程作業時，在承受環境載荷的同時，還有可能與過往的船只、補給船、守衛船等船舶發生碰撞，根據WOAD數據庫對海洋平臺給出的嚴重災害事故發生頻率統計數據，無論是固定式平臺還是移動式平臺，船舶碰撞都是最主要的風險因素。本文以1艘5000噸級補給船以不同速度（分別為 v=0.5 m/s，v=2 m/s，v=4 m/s，v=6 m/s）正碰某Truss Spar平臺水面浮體部分，采用有限元軟件Ansys/Ls-dyna建立Spar平臺和船舶三維有限元模型，并對碰撞過程進行模擬，對碰撞過程中的能量變化、撞擊力情況以及應力情況進行分析，得出一般性規律和結論，為Spar平臺的設計提供理論參考依據。

1 碰撞基本理論

1.1 碰撞問題的研究方法

船舶與海洋結構的碰撞是一個短暫的過程，但是卻包含了復雜的非線性過程，包含材料彈塑性變形為典型特征的材料非線性和以接觸摩擦為特征的狀態非線性。而且，在描述碰撞的狀態時，不光具有復雜的空間變量，更包含復雜的時間變量。

目前解決碰撞問題的方法主要有經典的Minorsky方法、漢斯-德魯徹理論、各種簡化解析方法、簡化內部機理的數值解法、試驗方法和有限方法等[2]。其中，顯示動力有限元仿真方法是碰撞領域最常用的數值計算方法。顯示動力學采用差分格式，不用求解切線剛度，不需要進行平衡，不存在收斂問題，并且在材料模型、接觸算法、并行計算方面也具有優勢。因此顯示方法特別適用于求解高速動力學事件和復雜的接觸問題。

1.2 碰撞運動方程的顯示求解

在本文所采用的Ansys/Ls-dyna軟件中求解船舶與海洋平臺碰撞這種具有高度非線性的動力學問題時一般采用顯示求解方法，其對于碰撞運動方程的顯示求解會用到有條件穩定的中心差分法，具體求解過程如下：

在總體坐標系下，如果當前時間步是步n，顯式運動微分方程[3]為

式中：M為結構質量矩陣，C為結構阻尼矩陣，K結構剛度矩陣，為外加載荷陣列，為包括碰撞力在內的外力分量，改寫為：

由式（2）可以得到加速度的表達方式：

在知識與信息飛速增長爆炸的時代，如何鑒別信息的真實性、準確性與有效性已經成為了當下的關鍵。因而，當今科學教育的研究潮流中批判性思維的培養已經成為了一個重要且亟待研究的方向，深度學習的基本特征中同樣包含了這點——對所學知識及其學習過程進行評判。生物學學科的教材內容體系與教師知識水平隨著生物科技的發展也需要不斷更新，學習過程為中心已經漸漸取代了多年前適用的教授過程為中心。前期的研究表明： 逆向化的教學主線應用在生物學模型課的教學中，能夠讓學生在評價知識與學習過程的同時，讓學生加強對學科知識的理解、學科思維的掌握以及學科精神的培育等[7]。

如果單元質量分布在節點上，則M為一對角陣，稱為集中質量矩陣，線性方程組將成為一系列關于自由度的獨立的一元一次方程，從而可以求得節點加速度為：

進而對時間進行積分即可獲得速度vi和位移di。這里采用中心差分的顯式格式來進行時間積分，其格式為：

顯示積分，通常情況下不需要對矩陣進行求解或分解，也不需要求解聯立方程組，不存在收斂性問題，計算速度比較快，時間積分的精度保證和自動控制計算時間步長的大小，則有穩定性準則來實現。同時，在運用中心差分法求解碰撞問題時需要特別注意時間步長的選取，它不能超過臨界時間步長。在實際使用中，臨界時間步長一般取近似表示，即以有限單元網格的特征長度除以應力波速，其表達式為：

由式（6）可以知道臨界時間步取決于材料特性（音速）和單元長度，而Ls-dyna可以自動計算尺寸，一般不需要用戶自己重新定義。

2 有限元模型單元及材料的選取

2.1 有限元模型的建立

Truss Spar結構形式分為上部組塊、主體硬艙、桁架結構（連接硬艙和軟艙，包括垂蕩板）、底部軟艙、立管系統和系泊系統。平臺的底部壓載艙有永久的固體壓載和可變壓載2部分，固體壓載用以提升穩定性，而可變壓載能夠注入海水以便在安裝和作業中調節穩性。平臺及碰撞船的相關參數如表1所示。

表1 Truss Spar 主要參數Tab.1 Main parameters of the Truss Spar platform

在建立碰撞船模型時，為減少建模工作量節省計算時間，有必要對模型進行一定的簡化。本文中平臺上層建筑以質量塊形式添加，未考慮立管系統和系泊系統。同時，由于主要考慮平臺的受力及變形，對于船舶形狀也采取了一定的簡化，碰撞有限元模型如圖1所示。

2.2 材料模型的選取

在船舶與海洋平臺的碰撞中，平臺和船舶均會發生一定的塑性變形，因此對于平臺采取隨動塑性材料模型[4]（Plastic kinematics model），該模型是各向同性、隨動硬化或各向同性和隨動硬化的混合模型，且與應變率相關，能夠很好地模擬結構在碰撞中的塑性變形。具體參數如表2所示。

圖1 Truss Spar平臺碰撞有限元模型Fig.1 Finite element model of ship collision with Truss Spar platform

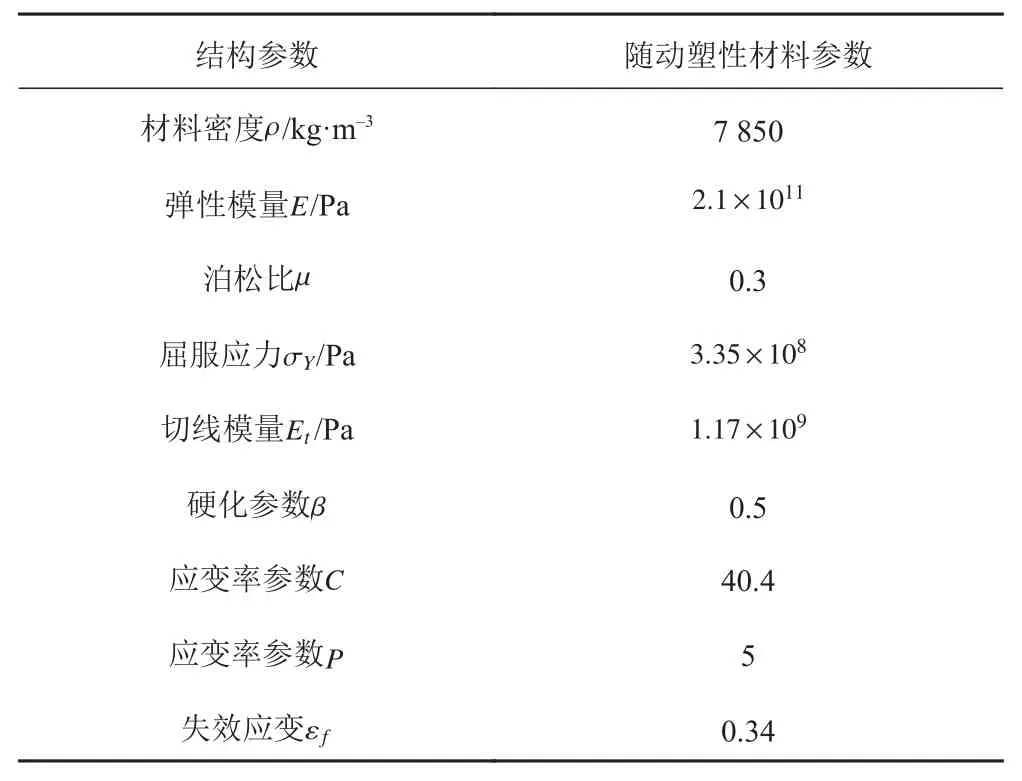
表2 平臺材料模型主要參數Tab.2 The main parameters of the material model platform

此外，在碰撞中船舶的變形主要發生在碰撞體接觸的船首部區域，船中后部區域不會發生變形，僅提供剛度和質量的影響[5]。因此，在建模時僅建立船體靠船首的部分船體，船首采用隨動塑性材料，其余部分采用剛體材料，材料參數如表3所示。

2.3 邊界條件的施加及流體的處理

在碰撞仿真中需要給模型施加一定的邊界條件，以防止在碰撞中發生剛體位移。位移邊界條件具體施加情況為：在硬艙浮筒底部平面上選取3個不共線的節點施加位移約束[6]，每個節點施加位移邊界條件（假設3個節點分別為節點1、節點2和節點3，那么邊界條件為：在節點1約束x方向位移，節點2的x、y方向位移，節點3的x、y、z方向位移）。同時，在碰撞過程中流體的影響也不可以忽略。目前對于碰撞過程中流體的處理主要有流固耦合和附加水質量2種方法，本文選取附加水質量法來對流體進行處理。其原因在于附加水質量結果和流固耦合結果相差不大（最大誤差不超過10%），計算時間僅為流固耦合的2%[7]。

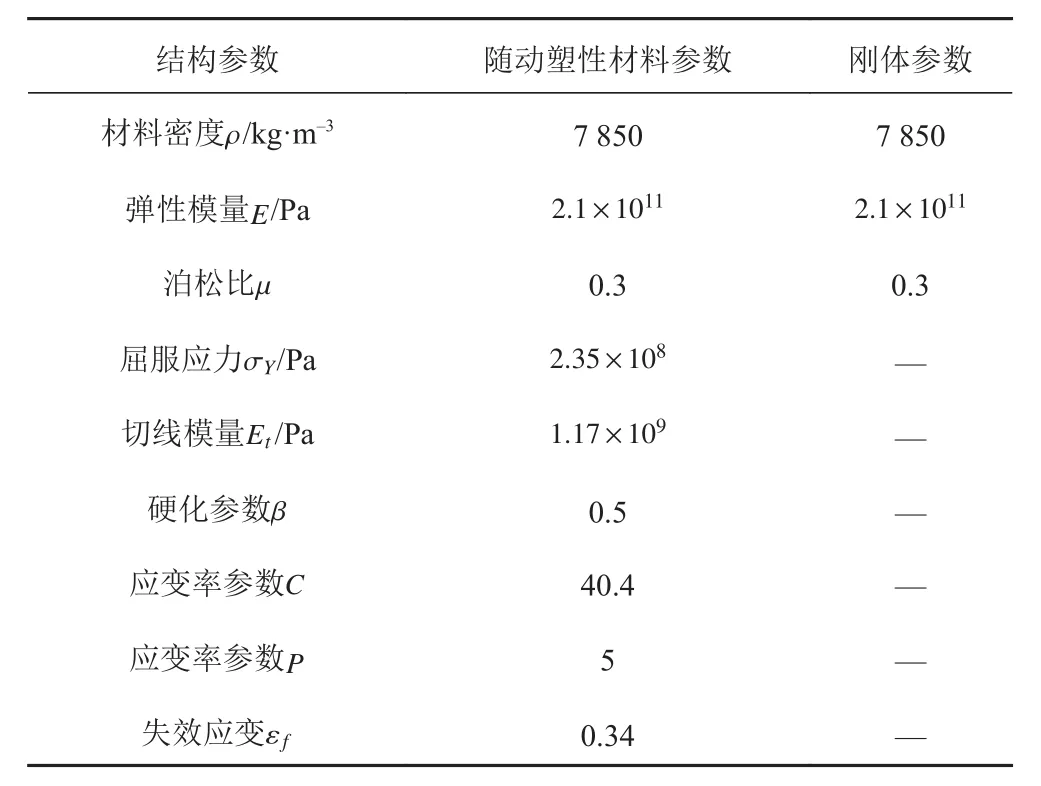
表3 船舶材料參數設置Tab.3 The main parameters of the material model ship

3 碰撞仿真結果及分析

3.1 碰撞過程中能量的分析

為研究碰撞中能量的變化，將平臺和碰撞船舶視為一個完整的系統，選取碰撞速度v=2 m/s進行分析，碰撞過程中系統各能量變化如圖2所示。

圖2 速度 v=2 m/s時的能量轉化曲線Fig.2 The energy conversion curve at velocity v = 2 m/s

由圖2可以得到在整個碰撞過程中，系統的動能在不斷減小，內能、沙漏能和摩擦能在不斷增加，即系統動能轉化為內能，同時產生了少量的沙漏能和滑移能。結合4條曲線變化的趨勢可以知道，系統中一部分能量減少，另一部分能量增加，總的能量變化是遵循能量守恒定律的。而從數值上看，系統中動能占主要部分最大時達到了9.28E+08J，其次是內能最大值達到了2.49E+07J，而沙漏能和滑移能相對較少，這說明當船舶撞擊Truss Spar平臺時，系統中能量的轉化主要發生在動能和內能之間發生，為此在研究不同船舶速度撞擊平臺中的能量變化時可以將精力集中在動能和內能。

圖3和圖4分別為船舶以不同速度（分別為v=0.5 m/s，v=2 m/s，v=4 m/s，v=6 m/s）撞擊 Truss Spar平臺碰撞系統內動能和內能的變化曲線。由圖3可知，在碰撞中速度越大系統動能越大，而在碰撞過程中，不同速度下系統動能都逐漸減少。從曲線變化趨勢來看，除了速度在0.5 m/s時系統動能曲線變化趨勢略有不同，其他速度下（v=2 m/s，4 m/s，6 m/s）大致相同，在碰撞初期動能急速降低，在運動相對穩定后，降低速度變緩。同樣，由圖4可知，在碰撞中速度越大系統內能越大，在整個碰撞過程中，系統內能都增加，其增加的速度在碰撞初期較大，隨后一段時間內相對平緩，隨后將保持在一定的增長速度不變。結合圖3和圖4來看，在同一速度下隨著系統動能的減少，系統內能在不斷增加，這在一定程度上印證了上文的結論。

圖3 不同速度下系統動能變化曲線Fig.3 System kinetic energy curve at different speeds

圖4 不同速度下系統內能變化曲線Fig.4 Variation curve of system energy at different speeds

3.2 碰撞過程中撞擊力分析

船舶以不同速度（分別為 v=0.5 m/s，v=2 m/s，v=4 m/s，v=6 m/s）撞擊 Truss Spar平臺過程中的撞擊力時間歷程曲線如圖5所示。撞擊力在一定程度上反映了平臺在遭受船舶碰撞時結構受損程度，對碰撞中撞擊力時間歷程曲線的分析有助于更好地認識在碰撞過程中平臺的運動情況。

圖5 不同速度下撞擊力時程曲線Fig.5 Time-course curve of impact force at different speeds

由圖5可以得到，當速度為0.5 m/s時，船舶低速運動一段時間，此時碰撞力為0，在發生碰撞的一瞬間碰撞力達到最大，同時構件發生變形以卸載部分撞擊力直至船舶與平臺分離，碰撞力再次降為0，碰撞持續時間較短；當速度為2 m/s時，在碰撞船舶運行極短的時間內即發生碰撞，此時碰撞力急劇攀升但未達到最大值，同時結構發生變形卸載部分撞擊力，在外圍結構變形結束后，碰撞波及平臺整體，碰撞力達到最大值，隨著運動繼續船舶與平臺仍會分離，碰撞力趨近與0；當速度為4 m/s和6 m/s時，船舶運動速度相對較大，在碰撞的瞬間撞擊力急劇增至最大值，隨后結構多次變形，撞擊力逐漸減小，在平臺和碰撞船分離后為0。但是由于浮動式平臺結構柔性較大，在碰撞后會發生回彈，與撞擊船舶發生二次碰撞，所以撞擊力在歸零后又會上升。從數值上看，在速度增大后撞擊力也隨之增大，而且曲線峰值（即最大撞擊力）出現的時間也越來越早（見表4）。總體來看，不同速度下的撞擊力時程曲線變化趨勢大致相同。

3.3 碰撞過程中結構應力分析

船舶與海洋平臺發生碰撞時，巨大的撞擊力會使結構產生很高的應力。圖 6 為船舶以 0.5 m/s，2 m/s ，4 m/s，6 m/s 速度撞擊 Truss Spar平臺結構撞擊力達到最大時的應力云圖。

由圖6可知，隨著撞擊船舶速度的增大，平臺結構產生的高應力的區域也越來越大，同時在撞擊接觸區域產生的應力也越來越大。但是，當平臺結構遭受的船舶撞擊力達到最大時，所對應時刻的應力并不一定最大，這可以從結構應力時程曲線得到驗證。

表4 不同速度下撞擊力最大值及出現時間Tab.4 The maximum impact force and time of occurrence at different speeds

結合表4和圖7可知，最大應力值不一定在最大撞擊力出現的時候出現，在撞擊力達到最大后的運動中結構仍會產生較高的應力。從數值來看，隨著速度的增大，應力值明顯增大，而且除了碰撞速度為0.5 m/s的曲線圖外，其余曲線中應力都在極短時間內超出鋼材屈服極限。而在曲線變化趨勢上，不同速度下應力變化趨勢大致相同，都是在碰撞瞬間應力急劇增加，隨后應力開始下降，最終上升一段時間后穩定在一定數值。這其中碰撞速度為0.5 m/s的應力曲線變化較為明顯，其原因是船舶速度較低在碰撞后船舶與平臺在較短時間內分離，應力下降較快，而后平臺因獲得速度繼續運動，結構之間因位移導致應力又開始增大并最終穩定在一定數值。

圖6 不同速度下撞擊力達到最大時應力云圖Fig.6 The stress nephogram at the maximum impact force under different speeds

4 結 語

本文以1艘5 000噸級補給船以不同速度（分別為v=0.5 m/s，v=2 m/s，v=4 m/s，v=6 m/s）正碰某 Truss Spar平臺水面浮體部分進行數值仿真模擬，通過對仿真結果的分析可以得到如下結論：

1）船舶與海洋平臺的碰撞是一個瞬態過程，在碰撞過程中能量轉化主要發生在動能和內能之間，同時伴隨有沙漏能和滑移能的產生。不同撞擊速度對碰撞響應的影響趨勢大致一致，隨著碰撞速度的增大，能量變化和結構損傷更大。

2）在對撞擊力的分析中可以知道，撞擊力時程曲線具有很強的非線性特性。在比較不同撞擊速度下的撞擊力時程曲線時得到，不同速度下的撞擊力時程曲線變化趨勢大致相同，隨著速度的增加撞擊力也在不斷增加且最大撞擊力出現的時間也隨著速度的增大出現的時間越來越早。

3）結合應力云圖和不同速度下的應力時程曲線可以知道，隨著撞擊速度的增大，平臺結構產生高應力的區域也隨之增大，接觸區域平臺應力也會增大。同時通過應力云圖可以得到，應力主要產生在船舶與海洋平臺發生碰撞的部位，在碰撞結束后，平臺結構會有一定的損壞，因此對于相應的位置在設計以及作業中必須考慮做對應的防撞措施，例如設置緩沖材料或配備守護船等。

圖7 不同速度下的應力時程圖Fig.7 Stress time histogram at different speeds