基于粒子濾波算法的方位跟蹤方法研究

周 彤，宋立臣

(大連測控技術研究所，遼寧 大連 116013)

0 引 言

在艦船水下輻射噪聲測量的過程中，安全、可靠地引導被測目標通過測量區域，并保證被測目標與測量系統之間的有效距離以滿足測試需求是極其重要的，也是一直關心的問題。現有的被測目標引導方法，往往依靠單一導航信標配合測距系統實現，通常僅提供被測目標與導航信標之間的單點距離信息，缺乏方位信息，使得目標實際航行軌跡與試驗要求軌跡有一定的偏差，造成測量單程無效，從而降低了測試效率，延長了試驗時間[1]。

目前方位估計算法的通常假設目標在觀測時間內為靜止狀態，即靜態方位算法，同時采用大計算量和多快拍數的批處理形式進行方位估計[2]。然而在實際情況下，目標通常為運動狀態，批處理方式的靜態方位估計方法不適用于實時連續跟蹤。同時，靜態方位估計方法是互不相關地估計2個連續時刻的方位信息，并沒有考慮到2個連續時刻狀態的關聯性，進而造成動態方位估計偏差較大。隨著對運動目標的測向精確度和實時處理的要求越來越高，靜態方位估計算法已不能滿足日益增長的需求，因此研究適用于動態目標的方位跟蹤算法成了一個新趨勢。本文將靜態方位估計中的MUSIC算法和粒子濾波跟蹤算法相結合，既提高了方位估計的精度更減小了計算量以適用于對目標的實時方位跟蹤。

1 AVS 和 MUSIC 方位估計算法

1.1 AVS 接收信號模型

通常在實際應用中矢量水聽器接收的水下目標輻射聲場為平面波聲場，因此假設聲源為平面波。則矢量水聽器接收的聲壓和振速的關系為

實際應用中處理的信號為離散信號，一般采用快拍數對每時刻數據進行批處理。假設快拍數為N在k時刻的聲源信號為

接收信號包含方位角和俯仰角信息，進而可以對數據進行方位估計。

1.2 MUSIC 方位估計

MUSIC算法作為子空間特征分解相關算法的代表，實現了方位估計技術向高分辨的發展。MUSIC算法的核心思想是利用數據的自相關矩陣的內在結構特性，將數據的協方差矩陣分解為和陣列流形一致的信號子空間，以及與信號子空間正交的噪聲子空間，并利用2個子空間的正交性，通過對譜峰進行搜索來估計信源的方位。

工程實際中，為提高信號處理的精度，采用多快拍數的觀測數據。設快拍數為L，則接收數據的自相關矩陣可表示為

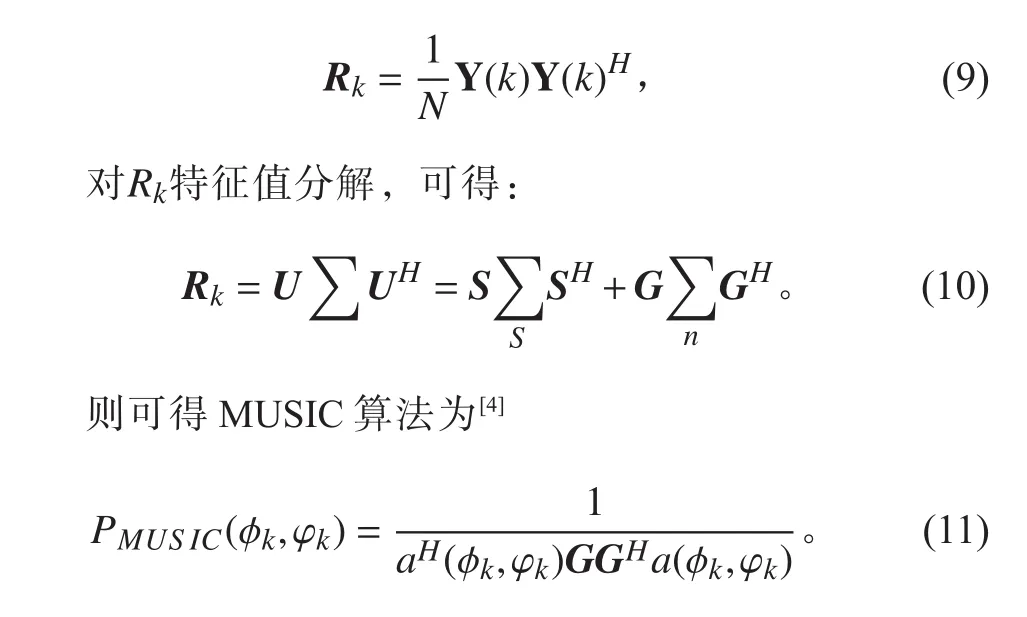
其中，G為與噪聲相關的特征值矩陣對應的噪聲子空間。

因此，通過譜估計式（11）的峰值搜索估計和峰值相對應的角度值即為入射的方向信息。

在信噪比（SNR）相對較高的噪聲環境中，MUSIC方法能夠通過如圖1所示的尖銳峰值來呈現聲源DOA。聲源真實方位為（20.5°，40.5°），然而，當SNR低時，峰值可能失真并且估計的DOA可能遠離真實位置，如圖2所示。

圖1 MUSIC 方法 DOA 估計性能 SNR=10 dBFig.1 DOA estimated performance based on the MUSIC algorithm SNR=10 dB

圖2 MUSIC 方法 DOA 估計性能 SNR=-10 dBFig.2 DOA estimated performance based on the MUSIC algorithm SNR=-10 dB

2 基于粒子濾波算法的方位跟蹤方法

為了給出DOA跟蹤問題的總體框架，首先定義狀態空間模型。假設目標聲源當前方位為，并以（rad/s）的速度移動。因此，目標聲源的狀態可以由當前方位和運動速度構成，即。采用勻速模型CV（Constant Velocity）模擬單信源的方位角度變化情況[5]，DOA的運動速度為常數。則狀態空間模型為

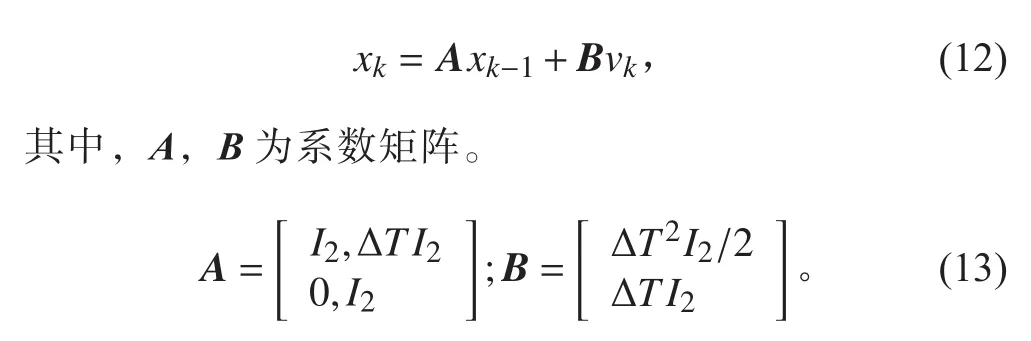
矢量水聽器的輸出矩陣是天然的觀測模型，即為式（7）。采用基于遞歸方式的貝葉斯重要性采樣，并以預測和更新的方式實現狀態估計[6]。

因此粒子權重在算法的濾波性能上具有重要的作用。當粒子接近真實位置時，粒子的似然函數具有較大的權重，則為了讓粒子在更新時使權重大的粒子能夠在重采樣時取代權重小的粒子，由式（20）可知似然函數的確定是算法性能的關鍵。假設測量的過程噪聲為高斯噪聲，則似然函數的最大似然估計為[9]

似然函數的主瓣通常比較平緩，尤其在低信噪比的條件下，因此不能有效的通過權重衡量真實狀態周圍的粒子并且可能出現虛假峰值。同時當快拍數很大時，將會導致粒子的權重接近于0，進而導致對粒子的權重估計失效。

因此引入MUSIC方法作為似然函數，即

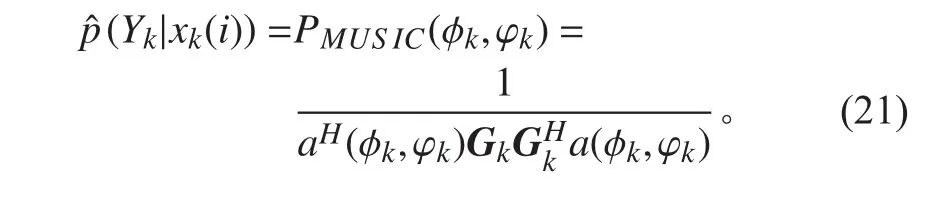
則似然函數被重塑，以增強在高似然區域采樣粒子的權重。這一步非常重要，因為它能夠幫助后續重采樣算法更有效地選擇和復制粒子。

給出最終PF-MUSIC方法的流程為

步驟1 初始化：采用隨機方法估計初始角度，從均勻分布中采樣，粒子數為N，。初始化各粒子權重為。

步驟7 令k=k+1，重復步驟2～步驟7。直到k＞T時，終止計算。

3 方位跟蹤方法性能驗證分析

3.1 仿真分析方位跟蹤方法性能

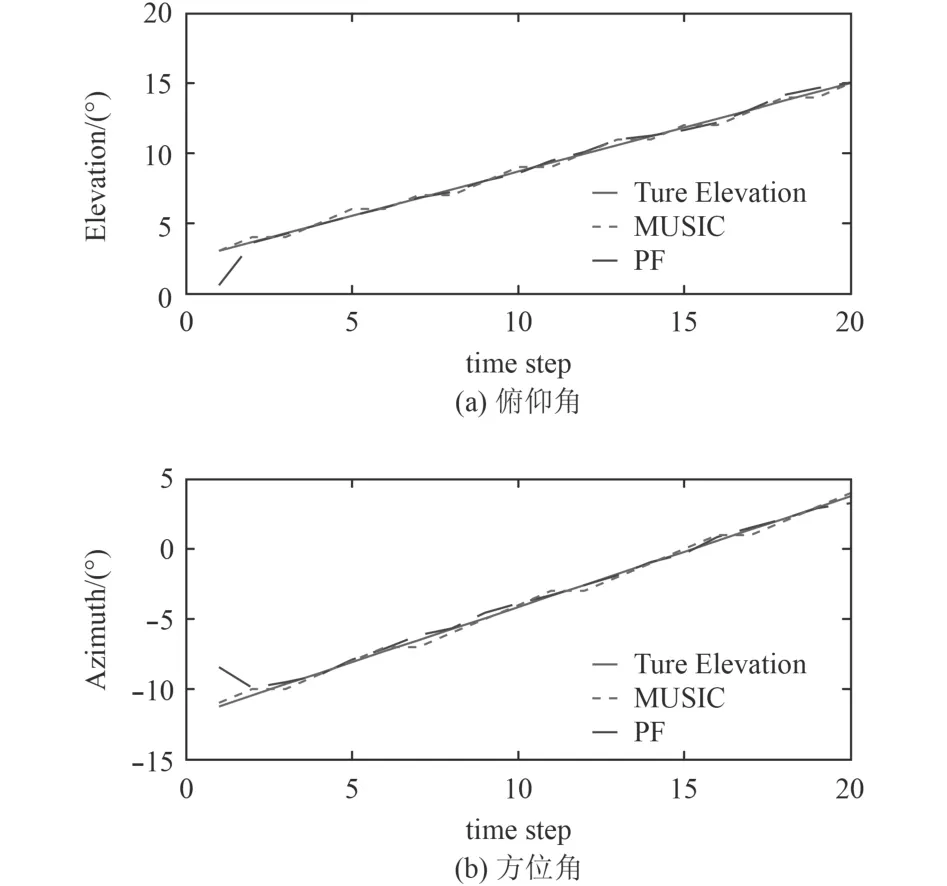
圖3 SNR=10 條件下的方位跟蹤Fig.3 DOA tracking under the condition of SNR=10 dB

圖3 給出了MUSIC方法和PF-MUSIC跟蹤方法的DOA跟蹤性能。MUSIC方法的性能在多個時間步長處，DOA估計結果遠離真實軌跡。然而，PF-MUSIC方法能夠結合來自聲源的動力學模型的時間信息以及來自當前測量時刻的空間信息，從而能夠一致地跟蹤聲源方位。它能始終鎖定聲源，并呈現令人滿意的DOA跟蹤。另外，雖然初始DOA對于PF-MUSIC方法是未知的并且被假定為均勻分布，但PF-MUSIC跟蹤方法能夠快速地收斂到真實軌跡。

為了充分評估跟蹤性能，采用50次蒙特卡羅平均模擬均方根誤差（RMSE）。如果絕對誤差小于1°，則被認為是正確的估計。圖4給出不同SNR下對RMSE的影響。采用從-10 dB～0 dB 的不同 SNR，以 2 dB的增量產生噪聲環境。

由于結合了時間信息，所提出的PF-MUSIC跟蹤算法在估計DOA方面比MUISC方位方法執行得更好。PF-MUSIC跟蹤算法即使在非常低的SNR環境下（例如，SNR=-10 dB），依然能夠保持對聲源DOA的鎖定。同時，PF-MUSIC方法不需要對角度進行三維搜索，在計算量上遠低于MUSIC方法，更適用于對目標的實時方位跟蹤的需求。

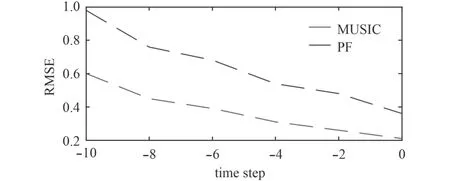
圖4 不同快拍數和 SNR 下的 RMSEFig.4 RMSE under the conditions of different snapshots and SNR

3.2 海上試驗驗證

2017年8月，在大連海域水深60 m區域，試驗驗證實時方位跟蹤方法的性能。信標的導航信號為4 kHz的單頻CW脈沖信號，脈沖周期為T=2 s。水下目標和導航信標正橫距離大于100 m，則聲場可視為平面波聲場。

為驗證方位跟蹤方法的實際性能，這里采用短基線方位方法作為對比方案。分別在目標首部和尾部各安裝2個接收器，用以接收導航信標信號。基線長度為 53 m。

試驗所采用的矢量水聽器為二維球型，典型的矢量水聽器接收的聲壓及振速的功率譜如圖5所示。

短基線和PF-MUSIC方法的跟蹤效果如圖6所示。

可知PF-MUSIC方法的方位跟蹤效果良好，并且與短基線方位相比曲線更平滑，適用于水下目標的實時方位跟蹤。同時，僅需在艦船上加裝單矢量水聽器即可滿足測試要求，更適用于工程實際。

4 結 語

將粒子濾波算法和MUSIC方法相結合，應用于矢量水聽器接收的水下運動目標數據的處理，有效地對運動目標的方位進行跟蹤。采用CV模型對聲源運動狀態進行建模，將MUSIC方法的估計函數作為粒子濾波算法中的似然函數，有效改進了在低信噪比條件下的跟蹤性能。通過結合時間和空間信息，PF-MUSIC跟蹤方法在二維DOA跟蹤中優于傳統的MUSIC方法，并且不需要空間搜索降低了計算量，適用于對目標的實時跟蹤，同時在較低信噪比的條件下也能夠獲得較好的精度，對水下目標的實時方位跟蹤上有較好的應用前景。

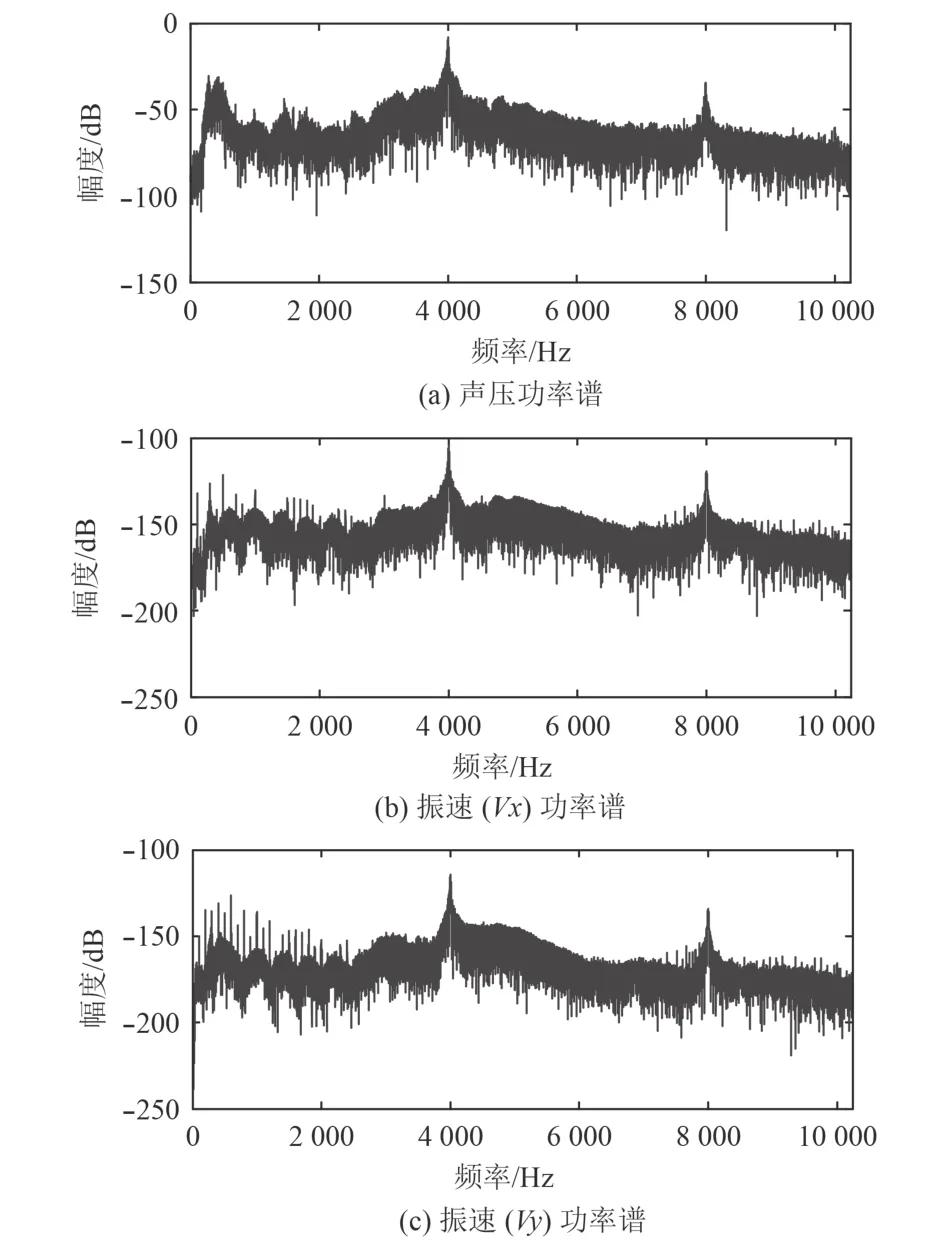
圖5 矢量水聽器接收聲壓和振速信號的頻譜Fig.5 Spectrums of Sound pressure and vibration speed received by the vector hydrophone

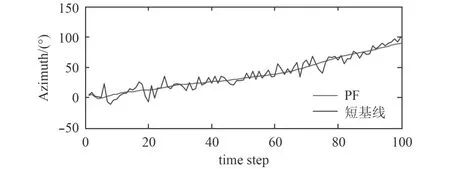
圖6 方位跟蹤效果Fig.6 The effect of DOA tracking