微分分次Poisson Hopf代數的張量積

胡獻國,郭夢甜,呂家鳳

(浙江師范大學 數學系, 浙江 金華 321004)

0 引 言

Poisson代數的概念起源于Poisson幾何, 可簡單看作交換代數與Lie代數的結合. 近年來，隨著Poisson代數的廣泛應用, 得到了多種Poisson代數的推廣形式[1-4]. 特別地, DRINFEL’D[5]定義了Poisson Hopf代數，詳細研究了這類代數在Poisson-Lie群上的應用. 此外, 呂家鳳等[6]給出了Poisson Hopf代數及其泛包絡代數的基本性質. 微分分次代數起源于代數拓撲與表示理論, 在交換代數與非交換代數領域有重要作用[7-8]. 作為其推廣, LYU等[9]引入了微分分次Poisson代數, 研究了這類代數的張量積及相關性質和應用. 受此啟發, 本文嘗試將Poisson Hopf代數的概念推廣到微分分次的情形, 定義了p次微分分次Poisson Hopf代數, 并推廣了文獻[9]的相關結果： 證明了任意2個p次微分分次Poisson Hopf代數的張量積仍為p次微分分次Poisson Hopf代數; 證明了p次微分分次Poisson Hopf代數構成的范疇dg-PHA是對稱monoidal范疇.

本文的主要結果如下：

定理1(1) 設(A,uA,ηA,ΔA,εA,SA,{·,·}A,dA)和(B,uB,ηB,ΔB,εB,SB,{·,·}B,dB)是任意2個p次微分分次Poisson Hopf代數，則

(A?B,u,η,Δ,ε,S,{·,·},d)

也是p次微分分次Poisson Hopf代數.相關運算定義為：

S(a?b)∶=SA(a)?SB(b),

η(1k)∶=1A?1B,ε(a?b)∶=εA(a)εB(b),

u((a?b)?(a′?b′))∶=(-1)|a′||b|aa′?bb′,

Δ(a?b)∶=(-1)|a(2)||b(1)|a(1)?b(1)?a(2)?b(2),

d(a?b)∶=dA(a)?b+(-1)|a|a?dB(b),

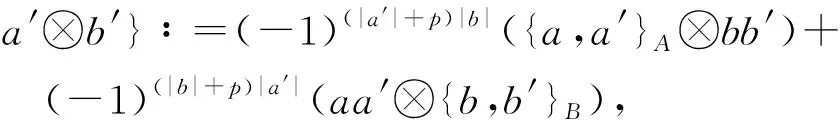
其中,uA(a?a′)∶=aa′,uB(b?b′)∶=bb′,

ΔA(a)∶=a(1)?a(2), ΔB(b)∶=b(1)?b(2), ||表示齊次元的次數,a,a′∈A,b,b′∈B為齊次元.

(2) 記dg-PHA為p次微分分次Poisson Hopf代數構成的范疇, 則dg-PHA是對稱monoidal范疇, 其左單位元與右單位元均為基礎域k.

(3) 設Aop與Bop分別為A與B的p次微分分次Poisson Hopf反代數. 則

(A?B)op=Aop?Bop.

1 p次微分分次Poisson Hopf代數

首先，回顧一些后面要用到的概念.

如無特別說明, 文中所有代數均含有單位元1,k表示特征為0的基域, 所涉及的對象都是域k上的向量空間, 所涉及的分次均為Z-分次. 對任給的分次向量空間V與W, 扭轉映射是指

T：V?W→W?V∶T(v?w)=(-1)|v||w|w?v,

其中，v∈V,w∈W.

文中的分次代數A為Z-非負分次代數(A,u,η), 其中A=⊕n≥0An滿足A0=k,u∶A?A→A與η∶k→A分別被稱……