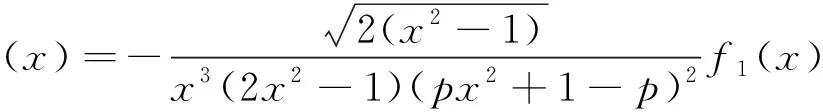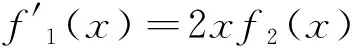Sándor-Yang平均關(guān)于經(jīng)典平均凸組合的確界

張帆, 楊月英, 錢偉茂

(1. 湖州職業(yè)技術(shù)學(xué)院 建筑工程學(xué)院, 浙江 湖州 313000； 2. 湖州職業(yè)技術(shù)學(xué)院 機(jī)電與汽車工程學(xué)院, 浙江 湖州 313000；3. 湖州廣播電視大學(xué) 遠(yuǎn)程教育學(xué)院， 浙江 湖州 313000)

0 引 言

2013年,YANG[1]介紹了4個(gè)Sándor-Yang平均：

(1)

其中，

(2)

(3)

分別為2個(gè)正數(shù)a和b的幾何平均、算術(shù)平均、二次平均, Neuman-Sándor平均[2-3]和第二類Seiffert平均[4], 第一類Yang平均和第二類Yang平均[5-7].

設(shè)p∈R，a,b>0, 則調(diào)和平均H(a,b),反調(diào)和平均C(a,b)和p階冪平均Mp(a,b)[8]分別定義為

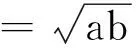
(4)

并且p階冪平均Mp(a,b)對于固定的a,b>0和a≠b關(guān)于p∈R是連續(xù)和嚴(yán)格單調(diào)上升的.

不等式

H(a,b)=M-1(a,b)

L(a,b)

NS(a,b)

C(a,b)

和

L(a,b)

NS(a,b)

對所有a,b>0且a≠b均成立,其中，P(a,b)=(a-b)/[2sin-1((a-b)/(a+b))]和L(a,b)=(b-a)/(lnb-lna)分別為2個(gè)正數(shù)a和b的第一類Seiffert平均和對數(shù)平均.

最近, Sándor-Yang平均關(guān)于其他二元平均或其組合的比較研究取得了一定進(jìn)展. 國內(nèi)外學(xué)者證明了在特殊情形下一些涉及Sándor-Yang平均的重要不等式[1, 9-14].

Mα(a,b)

Mλ(a,b)

對所有a,b>0且a≠b成立的最佳參數(shù).

徐會(huì)作[13]證明了雙向不等式

α1Q(a,b)+(1-α1)A(a,b)

β1Q(a,b)+(1-β1)A(a,b)，

α2Q(a,b)+(1-α2)A(a,b)

β2Q(a,b)+(1-β2)A(a,b),

α3C(a,b)+(1-α3)A(a,b)

β3C(a,b)+(1-β3)A(a,b),

α4C(a,b)+(1-α4)A(a,b)

β4C(a,b)+(1-β4)A(a,b)

對所有a,b>0且a≠b成立當(dāng)且僅當(dāng)α1≤1/3,

本文發(fā)現(xiàn)并證明了最佳參數(shù)α1,α2,α3,α4,β1,β2,β3,β4∈(0,1),雙向不等式

α1A(a,b)+(1-α1)H(a,b)

β1A(a,b)+(1-β1)H(a,b),

α2A(a,b)+(1-α2)G(a,b)

β2A(a,b)+(1-β2)G(a,b),

α3Q(a,b)+(1-α3)A(a,b)

β3Q(a,b)+(1-β3)A(a,b),

α4C(a,b)+(1-α4)A(a,b)

β4C(a,b)+(1-β4)A(a,b)

對所有a,b>0且a≠b均成立,并且推得一個(gè)新的不等式鏈：

G(a,b)

1 引 理

為證明本文的主要結(jié)論, 需以下引理：

引理1設(shè)p∈(0,1),

(1) 若p=5/6, 則對所有x∈(1,+∞)有f(x)<0;

證明經(jīng)簡單計(jì)算得

(5)

(6)

其中，

f1(x)=p(4-p)x6+2(3p2-2p-2)x4-

(7p2-10p+3)x2+2(1-p)2.

(7)

下面分2種情形討論：

(1) 當(dāng)p=5/6時(shí), 式(7)變?yōu)?/p>

(8)

對所有x∈(1,+∞)成立.

所以, 由式(5)、(6)和(8)易得對所有x∈(1,+∞)有f(x)<0.

6p-5=-1.878 4…<0,

(9)

2p2+14p-11=-3.175 0…<0,

(10)

3p2+8p-4=0.974 0…>0,

(11)

式(7)和式(9)～(11)經(jīng)簡單計(jì)算可得

(12)

(13)

其中，對所有x∈(0,+∞),

f2(x)= 3p(4-p)x4+4(3p2-2p-2)x2-

(7p2-10p+3),

f2(1)=2p2+14p-11<0,

(14)

4(3p2+8p-4)x>0.

(15)

由式(14)和(15)可得，存在λ0∈(1,+∞)，使得當(dāng)x∈(1,λ0)時(shí)f2(x)<0，當(dāng)x∈(λ0,+∞)時(shí)f2(x)>0.

由式(12)和(13)及當(dāng)x∈(1,λ0)時(shí)f2(x)<0可知，f1(x)<0.由式(13)和當(dāng)x∈(λ0,+∞)時(shí)f2(x)>0得到函數(shù)f1(x)在區(qū)間(λ0,+∞)上嚴(yán)格單調(diào)上升；則由式(12)和f1(λ0)<0及函數(shù)f1(x)在區(qū)間(λ0,+∞)上的單調(diào)性,可得存在λ1>λ0，使得當(dāng)x∈(λ0,λ1)時(shí)f1(x)<0，當(dāng)x∈(λ1,+∞)時(shí)f1(x)>0.

下面分2種情形討論：

情形1x∈(1,λ1].易由式(5)和(6)及在區(qū)間(1,λ1)上f1(x)<0得到f(x)>0.

情形2x∈(λ1,+∞).由式(6)和f1(x)>0，得到函數(shù)f(x)在區(qū)間(λ1,+∞)上嚴(yán)格單調(diào)下降. 由式(5)和f(λ1)>0及函數(shù)f(x)在區(qū)間(λ1,+∞)上的單調(diào)性，可得存在λ>λ1>λ0∈(1,+∞)，使得當(dāng)x∈(λ1,λ)時(shí)f(x)>0，當(dāng)x∈(λ,+∞)時(shí)f(x)<0.

引理2設(shè)p∈(0,1)，

(1) 若p=2/3, 則對所有x∈……