輥位參數對大徑厚比電阻焊管成形的影響
胡盛德 余 昊 陳 俊 李立新 潘成剛
(武漢科技大學鋼鐵冶金及資源利用省部共建教育部重點實驗室,湖北 武漢 430081)
隨著鋼結構行業的快速發展,一些大口徑薄壁焊管因單位質量輕,截面特性優而逐漸受到鋼結構設計者的青睞,如光伏電站太陽能支撐管、核主泵屏蔽套坯管等。對高頻直縫焊管,可穩定生產的徑厚比一般為15~90,但當圓管徑厚比為90時,屬于大徑厚比的特殊圓管,這類管在使用連續輥彎排輥成形生產時邊緣位移量大,極易出現邊浪、焊接不穩定等問題,難以保證焊管的綜合質量[1- 4]。另外,不合理的變形量分配還會加速對軋輥的磨損、加劇“反彎”現象而增加不必要的能耗[5]。因此,為了確定合理的成形工藝,本文通過有限元仿真分析研究了輥位參數對大口徑薄壁管成形的影響。研究參考了某種規格產品原始下山量及輥位參數,以成形過程中板帶橫截面縱向應變的方差最小、等效塑性應變均勻、待焊邊部形態好和產品無邊浪為目標,對下山量和底輥輥位參數進行優化,并在此基礎上,以待焊邊部形態好、反彎最小為目標對軋輥開口度進行優化。
1 動力學基本理論知識
求解域動力顯式方程可表示成:

(1)

運用中心差分法求解式(1)。時刻的離散速度、加速度中心差分公式分別為:
(2)
(3)
將式(2)、式(3)代入式(1),可得求解各個離散時間點位移值的遞推公式:
(4)
為了使該算法趨于穩定值[6- 7],運用顯示算法直接求解,在條件穩定的要求下,需要較小的時間步,且保持狀態足夠穩定,即時間步長必須小于該問題求解方程性質根據 Courant- Fried Richs- Levy穩定性準則所決定的臨界值。在非線性和非線性接觸存在內力矢量中包含的內力可以不用在檢查中收斂。
2 排輥成形有限元模型
在建立彈塑性有限元模型的過程中,準備φ508 mm的產品,以HFW660直縫焊管排輥成形為例。參考生產實際,成形帶鋼尺寸選為24 000 mm×1 580 mm×5.6 mm,材料為X60管線鋼,其彈性模量E=210 GPa,泊松比μ=0.3,密度ρ=7 800 kg/m3;網格采用三維4節點有限薄膜應變殼單元(S4R)劃分;實際生產速度為0.2 m/s。為了減少計算時間同時保證較高的計算精度,研究中嘗試了不同的板帶速度,發現速度設為2 m/s較為合適,此時滿足系統動能小于內能5%的要求[6- 7];選擇通用接觸,軋輥設為主控面;采用庫倫摩擦,摩擦因數設為0.1;排輥成形過程中,板帶中心只能沿成形方向前進,橫向不能有位移,因此設置板帶中心線上節點的橫向位移為0。考慮到生產過程中軋輥的變形極小,設置軋輥為剛體[5],其網格劃分采用3節點三維三角形剛體單元(R3D3)。由于對稱性,只需建立1/2模型[8],如圖1所示。
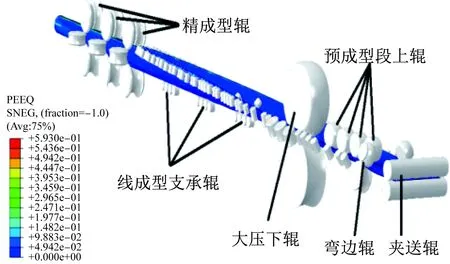
圖1 HFW焊管排輥成形過程有限元模型Fig.1 FEM model of cage- roll forming for HFW pipes
3 仿真結果及變形規律討論
3.1 試驗驗證
為了驗證有限元模型的正確性,對比板帶關鍵位置的開口度和板帶邊緣深度的模擬值和計算值,如表1所示。其中開口度是指板帶兩邊緣之間的水平距離,位于變形板帶的橫截平面中,而板帶邊緣距中心處的豎直距離則是指邊緣深度。選取對比點為:預成形段P1、P2處、線成形段L1、L3處,其到夾送輥縱向距離分別為ZP1=4 560 mm、ZP2=7 100 mm、ZL1=10 400 mm、ZL3=16 600 mm,如圖2所示。
由表1可見,邊緣深度的誤差值在1.2%~2.6%之間,開口度的誤差為1.2%~3.5%之間。與實際生產的吻合度較高,說明了有限元模型的可靠性。

表1 關鍵位置邊緣深度和開口度的模擬值與實測值的對比Table 1 Comparison of simulated and measured values of height of cross- section and opening value at different positions

圖2 成形方向測量位置示意圖Fig.2 Schematic diagram of measurement positions along forming direction
3.2 輥位參數對大徑厚比高頻焊管成形的影響
為了保證鋼板邊部縱向應變盡量小和縮短成形機組長度,HFW660直縫焊管排輥成形通常采用下山法成形,所謂下山法就是在成形過程中板帶底部呈逐漸下降趨勢[1]。本文將HFW660直縫焊管排輥成形機組的軋輥分為兩部分:軋輥的約束開口度和下山量,及其約束成形底線。夾送輥、預成形內輥、大壓下輥往往存在于約束成形底線及下山量的軋輥中,并且線成形段支承輥及內輥、精成形段軋輥在其中也有不少涉及。約束成形底線的軋輥輥位參數變化的表現形式很多,本文采用下山量H及下山曲線的變化來表示。在試驗中發現,在采用下山法成形直縫焊管情況下,成形底線體現在預成形段和線成形段有一定幅度的減少,因此,本文以精成形入口處帶鋼中心線與夾送輥帶鋼中心線間的豎直距離來表示下山量H,如圖3所示。同時,以開口度W的增減來約束開口度軋輥的輥位參數值,且約束開口度的軋輥主要有彎邊輥、預成形和線成形段的排輥。
3.2.1 下山量及下山曲線的影響
采用下山法成形時,為了達到最佳成形效果,約束成形底線及下山量的軋輥底部的連線呈圓滑過渡的曲線,從而使下山成形阻力降到最低,因此最優的下山曲線理論上符合二次函數形式,可以用二次曲線來擬合[1]。坐標原點O設在板帶中心的夾送棍處,x軸正向設為板帶軋制成形方向,豎直向上為y軸正向建立坐標系(見圖3),設成形底線的曲線函數為:

圖3 下山法成形底線示意圖Fig.3 Schematic diagram of downhill method in roll formation
y=ax2+bx+c
(5)
參考原始輥位參數,固定夾送輥、保持預成形段和線成形段下山量的比例不變,對下山量為H=0.8D(D為圓管直徑)的φ508 mm直縫焊管的原始輥位成形底線,利用Origin軟件進行二次曲線擬合,得到:
y=6.299 87×10-7x2-0.034 43x
(6)
不同焊管生產單位根據成品尺寸選擇的下山量不同,但一般在H=(0.4~1.2)D范圍內。為了進一步比較不同下山量及下山曲線對直縫焊管成形的影響,除原始輥位下山量外,本文還選擇H=0.4D、0.6D、1.0D、1.2D等下山量,采用同樣的方法擬合下山曲線,所有下山曲線的函數系數見表2,其所對應的函數圖像(成形底線)如圖4所示。

表2 下山曲線函數系數Table 2 Functional coefficients of downhill curves

圖4 下山曲線函數圖像Fig.4 Function curves of downhill formation
將約束成形底線及下山量的軋輥如彎邊輥、預成型上輥、大壓下輥等的輥位橫坐標x值代入上述下山曲線函數,得到輥位新的縱坐標y值,以此來指導軋輥的上下調整,保持其他成形參數不變,進行有限元模擬計算,得到下山效果、等效塑性應變及待焊邊部形態,如圖5~圖9所示。
由圖5可見,H=0.4D下山量時,管坯最大等效塑性應變值為0.407 7;出精成形后的待焊管坯邊部鼓包邊浪比較明顯。
由圖6可以看出,H=0.6D下山量下,管坯最大等效塑性應變值為0.382 3;出精成形后的待焊管坯邊部有鼓包出現。

圖5 H=0.4D時的(a)下山效果、等效塑性應變及(b)待焊邊部形態Fig.5 (a)Downhill effect, equivalent plastic strain and (b) shape of the pending edge when H is equal to 0.4D
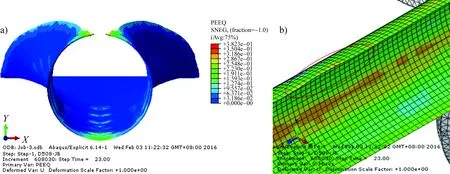
圖6 H=0.6D時的(a)下山效果、等效塑性應變及(b)待焊邊部形態Fig.6 (a)Downhill effect, equivalent plastic strain and (b) shape of the pending edge when H is equal to 0.6D
由圖7可見,原始下山量下管坯最大等效塑性應變值為0.371 2;出精成形后的待焊管坯邊部亦有輕微鼓包產生。
由圖8看出,H=1.0D下山量下,管坯最大等效塑性應變值為0.350 5;出精成形后的待焊管坯邊部較平直,成形狀態良好。
由圖9可見,H=1.2D下山量下,管坯最大等效塑性應變值為0.394 1;待焊管坯邊部有較輕微邊浪出現。
縱向應變不均勻是引起帶鋼邊浪等缺陷的主要原因,除等效應變和待焊邊部形態外,模擬還給出了因壓下量大而導致應變不均勻位置的板帶橫截面縱向應變的方差結果,圖10所示為不同下山量下,彎邊輥處(BD)及Fp1、Fp2、Fp3精成形3個道次處帶鋼橫截面上各點縱向應變的方差變化。可見,下山量的變化對應變方差有一定影響,其中精成形的首個道次處變化最大。從整個模擬過程看,下山量過大或者過小,均會導致4個位置帶鋼橫截面上縱向應變方差變大,在H=1.0D時,方差最小,板帶變形最均勻。

圖7 H=0.8D時的(a)下山效果、等效塑性應變及(b)待焊邊部形態Fig.7 (a) Downhill effect, equivalent plastic strain and (b) shape of the pending edge when H is equal to 0.8D

圖8 H=1.0D時的(a)下山效果、等效塑性應變及(b)待焊邊部形態Fig.8 (a)Downhill effect, equivalent plastic strain and (b) shape of the pending edge when H is equal to 1.0D

圖9 H=1.2D時的(a)下山效果、等效塑性應變及(b)待焊邊部形態Fig.9 (a)Downhill effect, equivalent plastic strain and (b) shape of the pending edge when H is equal to 1.2D

圖10 管坯截面縱向應變方差的對比Fig.10 Variance of longitudinal strains at cross sections of pipes
對比以上結果可知,采用HFW660焊管機組生產φ508 mm×5.6 mm直縫焊管,當下山量H=1.0D時,其管坯的待焊邊部較為平直,最大等效塑性應變最小,變形也最均勻,成形效果最好。
3.2.2 開口度的影響
由圖1可見一個三點彎曲結構,它由約束成形底線的上輥和預成形段和線成形段機架兩側對稱布置的一系列排輥及其底輥同時起作用。此結構效果明顯,相比于其他輥式成形結構,其帶鋼兩邊被排輥約束,使得帶鋼邊緣在成形過程中的回彈大大減小。因此,在軋制口徑不一的焊管時,無需重新變更軋輥,改變排棍的位置即可。排輥的自由度較多,成形位置的開口度受排棍的棍位影響,通過調整開口度,可以改變板帶在成形過程中的變形量分配并減少局部變形異常。在3.2.1節最優下山曲線的基礎上,對原開口度(W)分別增大3%,減小3%、6%、9%進行計算,其開口度分別表示為W1、W2、W3、W4。4種開口度下管坯待焊邊部形態如圖11所示。

圖11 不同開口度下待焊管坯邊部形態Fig.11 Edge shape of the pipe blank with different roller positions to be welded
由圖11可見,在開口度增大3%或減小9%時,焊接質量不佳,待焊管坯的邊部不平整;當開口度減小3%或6%時,出精成形段后,待焊管坯的邊部形態良好。圖12為下山曲線和開口度優化前后成形效果的對比,可見邊部褶皺消除,板帶邊部更加平直。

圖12 下山曲線和開口度優化(a)前、(b)后管坯成形效果對比Fig.12 Comparison of edge shapes of pipe blank (a)before and (b)after optimization of roller data
“反彎”[7]現象出現在排棍成形段管坯的彎曲成形過程中,主要是由于某些位置軋輥棍位不對所致。正確輥位下斷面弧線應呈外凸曲線,且圓心所標示方向在管坯中心線上,如圖13所示,圓心所在位置在管坯的外面,局部彎曲方向與整體彎曲方向相反。生產中則軋輥的外部出現缺陷,并且產生多余的能耗及“包辛格效應”(引起材料強度下降)[10],使管坯局部性能低于母材,導致產品不合格。
為了進一步了解開口度“反彎”情況,選擇開口度W2、W3,此開口度下,管坯邊部成形質量較好。在此,做如下要求:負值為反方向彎曲的圓弧的曲率,正值表示圓心在管坯內部的圓弧的曲率,負值曲率與反彎成正比。重點定位于軋制過程中帶鋼橫截面的相對曲率,對板帶橫截面上負值曲率的區域進行積分,如圖14所示。從圖14中可以看出,在開口度W3下反彎彎曲量最小,在線成形三段處也出現了反彎,隨著開口度的減小,反彎彎曲量均減小,且在大壓下輥處出現明顯的反彎。
4 結論
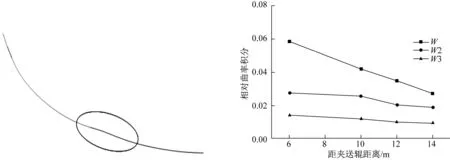
圖13 帶鋼橫截面反彎示意圖Fig.13 Schematic diagram of reverse bending at cross section of strip steel圖14 管坯負值曲率積分值 Fig.14 Negative curvature integral value of tube blank
(1)下山曲線及開口度對大徑厚比焊管排輥成形中板帶邊浪缺陷、反彎及能耗有重要影響,模擬結果可指導優化輥位,預防產品缺陷。
(2)對φ508 mm×5.6 mm直縫焊管的排輥成形,選取下山曲線、開口度時,板帶變形均勻、無邊浪缺陷,且成形中反彎小,多余能耗及“包辛格效應”也小。

