地震射線追蹤的線性走時擾動插值法

李同宇 張建中

(①海底科學與探測技術教育部重點實驗室，山東青島 266100； ②青島海洋科學與技術試點國家實驗室海洋礦產資源評價與探測技術功能實驗室，山東青島 266061； ③中國海洋大學海洋地球科學學院，山東青島 266100)

1 引言

地震射線追蹤及走時計算是地震學的基本問題之一，被應用于層析成像、地震定位、偏移以及地震數據采集設計等領域[1，2]。傳統的射線追蹤方法主要針對兩點射線追蹤問題，可分為試射法[3]和彎曲法[4]。這兩種方法都存在一定局限性： 前者需不斷試驗射線入射角，計算效率較低； 后者易于陷入局部最優解。20世紀80年代后期，出現了基于地震波前走時的射線追蹤方法，如程函方程的有限差分法[5-8]、最短路徑法[9-13]和線性插值算法[14-24]等。與傳統方法相比，該類方法具有較高計算精度和效率，得到廣泛研究和應用。

Asakawa等[14]提出基于線性插值的二維走時計算和射線追蹤方法(LTI)，指出由于可通過對LTI求導得到程函方程有限差分[5]公式，因而LTI方法可被視作程函方程有限差分法的更高版本，并對比說明了LTI方法具有更高的計算精度和效率。但是，LTI算法從震源開始逐步向外圍推進的過程中，考慮的波傳播方向有限，計算的節點處走時不一定是最小走時，也不能正確追蹤逆向傳播的射線。為了克服這些問題，該方法被不斷的修正和改進。張建中等[15，16]結合LTI與最短路徑算法，提出了動態網絡射線追蹤方法。黃月琴等[17]將二維LTI算法推廣至三維情形。Zhang等[18]結合雙線性走時插值和波前擴展法，提出了基于規則單元的三維射線追蹤方法，隨后Huang等[19]將該方法推廣至適用于不規則六面體單元。李培明等[20]提出了一種改進的雙線性插值射線追蹤方法，并結合動態變密度網格剖分，提高了旅行時的計算精度和效率。黃翼堅等[21]通過對傳統初至波LTI算法的射線方向進行約束，得到了一種直達波旅行時LTI迭代算法。張東等[22]通過使用LTI計算向前過程的離散旅行時場，并用B樣條插值梯度反向追蹤射線路徑，提出了初至波走時梯度射線追蹤算法(MTG)，較大程度消除了計算網格離散化帶來的誤差。在此基礎上，張婷婷等[23]結合逐次網格剖分技術及MTG方法，實現了三維層狀介質中的多波走時計算及射線追蹤，隨后針對在速度突變區域用B樣條插值計算旅行時梯度會帶來誤差的問題，張婷婷等[24]在三維MTG射線追蹤算法基礎上提出了一種改進的B樣條/線性聯合插值的三維射線追蹤(MMTG)算法。

LTI方法假設地震走時沿單元邊界線性變化，單元邊界上任意一點的走時可由該邊界上已知點走時的線性插值函數表示。但實際上，單元邊界上的走時呈非線性變化，因而當離散單元較大時，LTI方法的線性假設會導致較大的走時計算和射線追蹤誤差。針對這一問題，Zhang等[25]提出了基于規則單元的線性走時擾動插值(LTPI)方法，提高了波前走時的計算精度。為了更好模擬地形和地層界面的起伏及各地層速度的變化，本文將復雜介質模型離散成不規則單元，推導了二維情況下適用于不規則單元的LTPI方程，并結合波前擴展算法，提出了一種基于線性走時擾動插值的射線追蹤方法，數值實驗證明該方法具有較高的計算精度、效率以及很強的對復雜介質的適應性。

2 方法原理

基于LTPI的射線追蹤算法包括兩步：波前走時計算和射線追蹤。在波前走時計算過程中，根據惠更斯原理，結合群波前擴展算法(GMM)和LTPI方法，從震源開始逐步向外計算離散模型中各網格節點的波前走時；追蹤射線時，根據費馬原理，從接收點開始反向逐步確定射線與相關單元邊界的交點，直至追蹤至炮點，將炮點、各個交點和接收點順次連接，則得到從炮點到接收點的射線路徑。

2.1 模型離散

為模擬地形與地層界面的起伏，復雜模型被離散成如圖1所示的一系列不規則四邊形單元[19]。具體離散過程如下。

首先，在x方向等間距剖分模型。記模型在x方向的起始坐標為xc，剖分間距為Δx，剖分網格數目為n。離散模型的橫坐標可表示為

x(i)=xc+iΔxi=0，1,2,…，n

(1)

然后，由淺至深分別將每個地層劃分成多個薄層。在同一地層中，薄層數目相等，并且在同一x坐標處，各薄層在z方向上的厚度相等。不同地層的薄層數目可以不同。假設第k個地層中劃分的薄層數目為dk，則第k個地層中的第m個薄層在x=x(i)處的底面深度值可表示為

(2)

式中lk(i)和lk+1(i)分別表示第k個地層的頂面和底面在x=x(i)處的深度值。

這種離散方式可很好地擬合起伏地形和地層界面，不僅考慮了每個地層內速度的縱向和橫向變化以及地層速度與界面的耦合問題，且易于自動實現。

2.2 基于走時擾動插值的走時計算

在波前走時計算過程中，需計算與各級震源點相鄰的網格節點處的波傳播時間，即在一個單元內由已知節點走時計算未知節點走時。在單元較大時，LTI方法的線性走時假設會導致較大的計算誤差，因此本文引入線性走時擾動插值(LTPI)方法[25]，并將它擴展到適于不規則單元的情況。

在圖2中，假設射線穿過不規則單元的上頂邊界。S點表示震源點，P1和P2為單元上頂邊界兩個走時已知節點，坐標分別為(xi，zi)(i=1，2)，其波前走時分別為t1和t2。需計算射線從震源點S穿過單元上頂邊界傳至該單元邊界節點E的走時。

設從震源傳至E點的射線與單元上頂邊界的交點為P點，設上頂邊界的中點為P0(x0，z0)，P點坐標可表示為

(3)

式中：r為P點與P0點橫坐標之差，當P點在P0點右側時r大于零，否則r小于零；a0為常數，有

(4)

若P點走時為tP，則E點走時tE可表示為

tE=tP+slPE

(5)

式中：lPE表示P點至E點的射線長度；s表示該單元內的平均慢度。

現在采用LTPI方法[25]計算P點走時和坐標。將圖2中震源點S至單元上頂邊界之間的介質等效成勻速介質。在等效勻速介質中，從S點至單元上頂邊界的射線路徑為直線。若S點至P1、P2點的直線長度分別為l1、l2，則等效勻速介質的平均慢度seq可表示為

(6)

由此可求得等效勻速介質中從震源點S至點Pi(i=1，2)的射線走時為

(7)

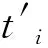
Δti=ti-seqlii=1,2

(8)

對于均勻模型，等效介質射線與實際射線重合，走時擾動為零。對于非均勻模型，等效勻速介質中的直射線與實際射線不同，走時擾動一般為非零值，且遠小于參考走時。

據式(6)～式(8)，P點處走時擾動可表示為

ΔtP=tP-seqlSP

(9)

式中lSP為等效勻速介質中S點至P點的射線長度。將式(9)代入式(5)，S點至E點的走時可表示為

tE=ΔtP+seqlSP+slPE

(10)

式中P點處的波前走時被分解為參考走時seqlSP和走時擾動ΔtP。其中參考走時由定義求得，而ΔtP可由單元邊界上已知點的走時擾動表示。

假定走時擾動沿單元邊界線性變化，P點的走時擾動ΔtP可用線性方程表示為

ΔtP=ar+b

(11)

式中a和b為常系數，可由P1和P2點處的已知走時擾動Δt1和Δt2表示

(12)

設炮點S坐標為(xS，zS)，E點坐標為(xE，zE)，據式(3)有

(13)

為簡化計算， 將lSP=f1(r)和lPE=f2(r)在r=0處分別進行泰勒級數展開，保留至二次方項，并把f1(0)和f2(0)分別簡化記為f1和f2，則有

(14)

其中

將式(6)、式(11)和式(14)代入式(10)中，由費馬原理可知，E點的波前走時滿足公式

(15)

求解式(15)可得

(16)

其中

由式(16)求得r值后，根據式(3)可知射線與單元上頂邊界的交點P的坐標，將r代入式(10)即可求得射線經過單元上頂邊界到達E點的走時。射線穿過單元其他邊界時的走時計算方法與此類似。

若不規則單元的其他邊界節點的走時也已知，同樣也可用上述方法求出射線穿過其他邊界到達E點的走時，然后將各個走時中的最小者作為所求E點處的波前走時。

2.3 波前擴展

本文采用群波前擴展算法(GMM)擴展波前。復雜介質離散后，每一個單元都被認為是均勻的，射線在單元內沿直線傳播。波前擴展的二維情形如圖1 所示。從震源點開始，利用LTPI計算出與其相鄰的各個網格節點上的波傳播時間，這些節點組成波前窄帶。在波前窄帶中需要按照一定規則找出次級震源點，再從次級震源點處開始計算與其相鄰的網格節點處的波傳播時間，這些網格節點便組成了新的波前窄帶[19]。波前窄帶需要不斷向外推進直至獲得介質中全部網格節點處的波前走時。

記當前波前窄帶為N，令

(17)

式中：sN，min表示波前窄帶各個網格節點中波傳播的最小慢度，即最大波傳播速度； Δx和Δz為波前窄帶各網格在x和z方向上的離散網格距。

由GMM算法可知若波前窄帶中兩個相鄰網格節點的波傳播時間之差小于δtN，則這兩點處的波傳播能量不會互相影響。次級震源集合G的選擇需遵循如下規則

G={(i,j)∈N,ti,j≤tN,min+δtN}

(18)

式中tN,min表示波前窄帶N中的最小波傳播時間。

波前走時計算步驟如下：

(1)將震源點的波前走時記為0，并且記M=2，表示該處已獲得波前走時； 其余網格節點的波前時間均記為無窮大，并令其M=0，表示該網格節點未計算波前走時；

(2)計算與震源相鄰的網格節點處的波的傳播時間后，將時間保存到波前窄帶N中，并令M=1，表示該處網格節點已計算出波傳播時間，但還未確定波前時間；

(3)波前窄帶中滿足式(18)的網格節點處的波傳播能量不會相互干擾，因此將其作為次級震源，將滿足條件的網格節點從波前窄帶N中移至次級震源集合G中，并令M=2；

(4)對次級震源集合G中的網格節點，更新與其相鄰的網格節點處波傳播時間，要注意相鄰網格節點需滿足M≠2，若節點處M=0，則將該節點移至波前窄帶N中并令M=1；

(5)若集合N非空，則跳轉至步驟(3)；若集合N為空，則波前擴展結束。

2.4 射線追蹤

在計算出復雜介質全部網格節點處的波前走時后，根據費馬原理和互換原理，可從接收點出發反向逐步確定出射線與相應單元邊界的交點，直至追蹤至炮點； 然后順次連接該對炮點和接收點之間確定的所有交點，便得到具有最小走時的直達波射線路徑。具體射線追蹤步驟如下。

(1)在接收點R所在單元內，利用LTPI方法計算射線路徑與該單元各邊界的交點P(圖3)。若接收點位于單元節點或單元邊界上，則需要在接收點所在的所有單元中進行計算。

(2)將具有最小走時的交點P作為新的接收點，判斷接收點是否位于炮點所在單元，若是，執行步驟(3)； 否則返回步驟(1)。

(3)順次連接炮點、射線與相應單元邊界的各個交點和接收點，就得到了該對炮點和接收點對應的直達波射線路徑。

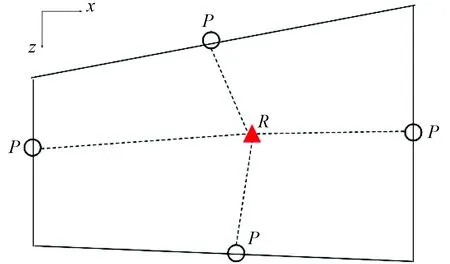
圖3 一個單元內射線路徑追蹤示意圖

3 數值實驗

為測試本文方法，設計了四種模型：均勻介質速度模型(模型1)、垂向漸變速度模型(模型2)、傾斜層狀速度模型(模型3)和含異常體速度模型(模型4)。前兩種模型的波前走時和射線路徑有解析解，可使用均方根誤差

(19)

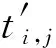
3.1 均勻介質速度模型

模型1是尺寸為2000m×2000m的均勻介質速度模型，離散為一系列80m×80m的規則單元。模型速度為4000m/s，震源坐標為(0，1000m)。圖4a和圖4b分別為用LTI和LTPI方法計算得到的波前走時(紅色虛線)與理論值(灰色實線)的對比圖，用相應方法計算的波前走時與理論值之間的絕對誤差分布分別如圖4c和圖4d所示。可見LTPI方法計算的波前走時更接近理論值，絕對誤差更小。

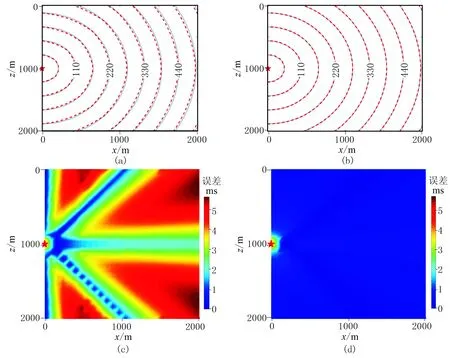
圖4 模型1波前走時等值線(單位：ms)及絕對誤差(a)LTI方法走時； (b)LTPI方法走時； (c)LTI方法誤差； (d)LTPI方法誤差

為說明計算誤差和計算時間隨離散單元大小的變化，對模型1分別以10、20、40、50、80、100和200m的網格尺寸進行離散，然后計算了LTI和LTPI方法的波前走時均方根誤差，并記錄了CPU時間(圖5)。可見在相同離散網格距下，LTI和LTPI方法所用CPU時間相近，而LTPI方法的均方根誤差值要遠小于LTI方法。隨著網格距的增大，LTI方法的均方根誤差值增長迅速，而LTPI方法的均方根誤差值則變化較為平緩。因此在一定誤差要求下，LTPI方法可以使用比LTI方法更少的單元數目，從而提高計算效率。

將模型1以80m的網格尺寸進行離散，分別使用LTI和LTPI方法計算射線路徑，與理論路徑的對比如圖6a和圖6b所示。使用相應方法計算的各個接收點對應的射線走時及其相對誤差對比分別如圖6c和圖6d所示。相比LTI方法，LTPI方法計算的射線路徑和射線走時更接近理論值。在不同接收點處使用LTPI方法得到的走時相對誤差穩定在1.0×10-3附近，小于LTI方法對應的誤差值。可見，LTPI方法具有更高的計算精度。

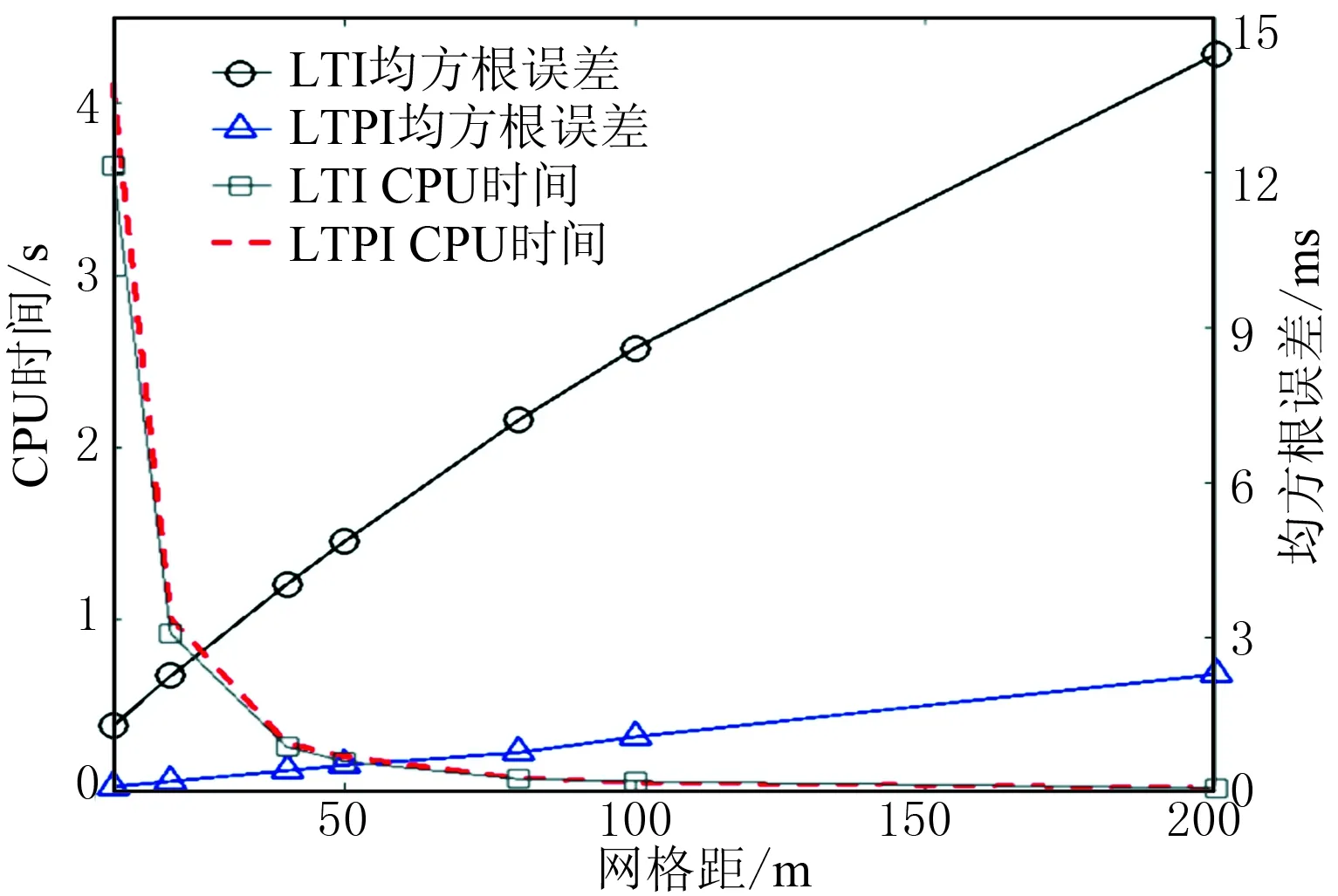
圖5 LTI和LTPI方法在不同離散網格距下的均方根誤差和CPU時間

3.2 垂向漸變速度模型

速度隨深度線性變化介質的波前走時和射線路徑具有解析解[26]。為將本文方法結果與變速介質的理論值進行對比，建立了速度隨深度線性增加的模型2，其尺寸為2000m×2000m，離散網格尺寸為40m×40m，速度隨深度線性變化函數為v=1500+2z(深度單位為m，速度單位為m/s)。炮點位于(1000m，0)。圖7a和圖7b分別為用LTI和LTPI方法計算出的波前走時(紅虛線)與理論值(灰實線)的對比圖，圖7c和圖7d分別是用相應方法計算的波前走時絕對誤差分布圖。可見LTPI方法比LTI方法計算的波前走時更貼近理論值，計算精度更高。

圖6 模型1的射線路徑及走時對比圖(a)LTI方法射線； (b)LTPI方法射線； (c)計算走時與理論走時； (d)計算走時相對誤差

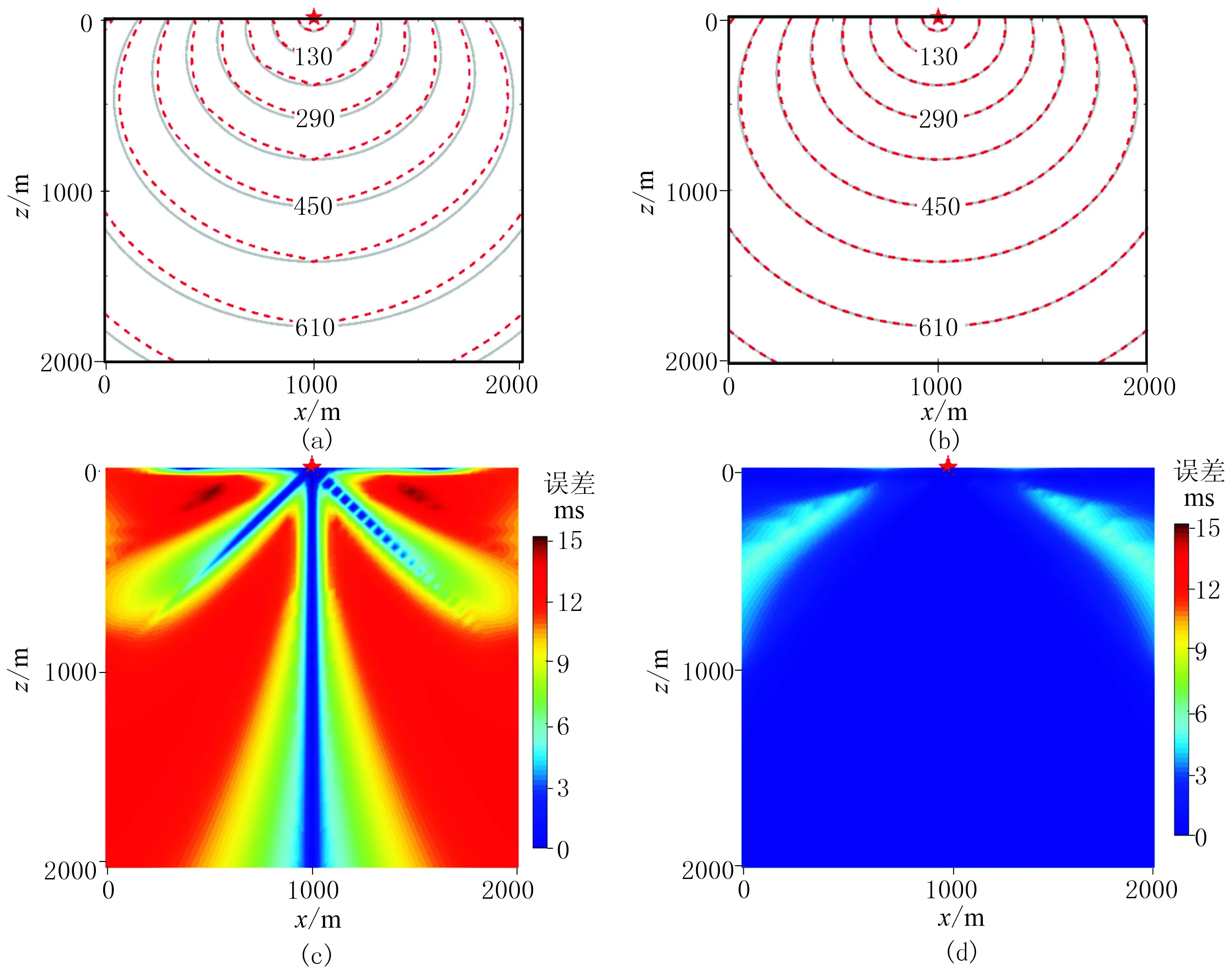
圖7 模型2波前走時等值線(單位：ms)和絕對誤差分布圖(a)LTI方法走時； (b)LTPI方法走時； (c)LTI方法誤差； (d)LTPI方法誤差

為說明本文方法對離散單元大小的響應，將模型2分別以10、20、40、50、80、100和200m網格尺寸做離散，分別用LTI和LTPI方法計算波前走時均方根誤差并記錄了CPU時間(圖8)。可見在同一網格距下，LTI與LTPI方法所用的CPU時間相近，但LTI方法的均方根誤差比LTPI方法大一倍以上。隨著網格距的增大，LTI方法的均方根誤差值快速增大，而LTPI方法的均方根誤差值變化相對平緩。因此在一定誤差要求下，LTPI方法可使用比LTI方法更少的單元數目以提高計算效率。

將模型2以40m的網格尺寸離散，炮點坐標為(1000m，2000m)，圖9a和圖9b分別為使用LTI和LTPI方法計算的射線路徑與理論路徑的對比圖，不同接收點處分別使用這兩種方法得到的射線走時及其相對誤差分別如圖9c和圖9d所示。可見在速度隨深度線性增加的模型中，使用LTPI方法得到的射線路徑和射線走時更加貼近理論值，并且對應的走時相對誤差要小于LTI方法。

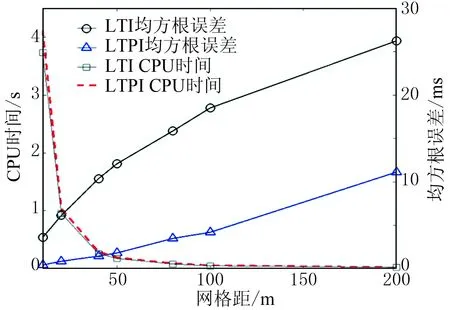
圖8 不同網格距下LTI和LTPI方法計算的均方根誤差和CPU時間

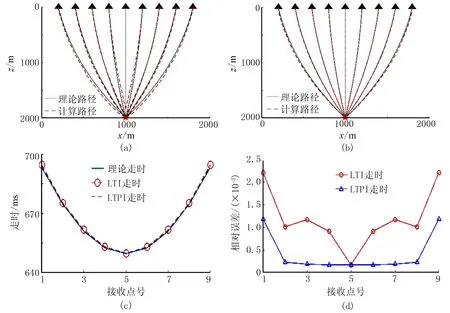
圖9 模型2中射線路徑及走時對比圖(a)LTI方法射線； (b)LTPI方法射線； (c)計算走時與理論走時； (d)計算走時相對誤差

3.3 傾斜層狀速度模型

模型3由三層傾斜層狀介質組成，各層速度從上到下分別為2000、3000和4000m/s。模型尺寸為2000m×2000m，震源位于(1000m，0)。分別使用LTI和LTPI方法計算離散網格距為20m(灰色實線)和80m(紅色虛線)時的波前走時(圖10)。可見離散網格尺寸變化時，使用LTPI方法得到的波前走時更加一致，與LTI方法相比，LTPI方法具有良好的穩定性，能更好地適應大網格距離散模型。

用網格距為40m的網格離散模型3。為獲取傾斜層狀介質中的理論射線路徑，先設定炮點位置為(1000m，1800m)，再從炮點處以一定的出射角出射射線，根據Snell定律確定射線路徑，將射線在地表的出射點作為接收點。然后分別使用LTI和LTPI方法計算了這些炮檢點所對應的射線路徑(圖11a和圖11b所示)。可見用LTPI方法計算的射線路徑更接近理論射線路徑。不同接收點處對應的射線走時及其相對誤差分別如圖11c和圖11d所示，使用LTPI方法計算得到的走時相對誤差穩定在1.0×10-3以下，小于LTI方法的相對誤差。實驗結果說明LTPI方法比LTI方法具有更高的計算精度。

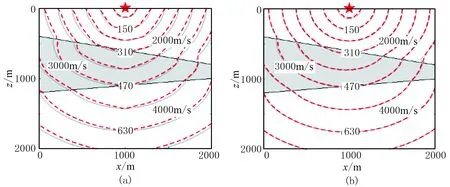
圖10 離散網格距分別為20m和80m時，模型3波前走時等值線圖(單位ms)(a)LTI方法； (b)LTPI方法

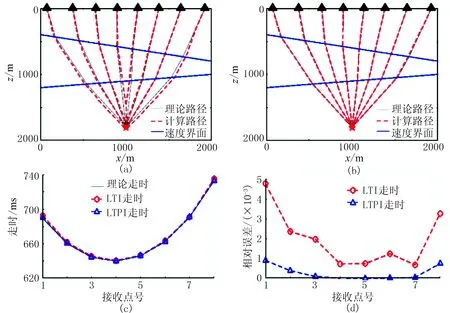
圖11 模型3中射線路徑與走時對比圖(a)LTI方法射線； (b)LTPI方法射線； (c)計算走時與理論走時； (d)計算走時相對誤差

3.4 含異常體速度模型

模型4尺寸為2000m×2000m，由三層起伏層狀介質組成，從上到下速度分別為1700、2800和1800m/s。在上層介質中存在速度為2100m/s的高速體，中間層介質含一速度為2300m/s的低速體。震源位于(1000m，2000m)。分別用LTI和LTPI方法計算了離散網格距為20m(灰色實線)和80m(紅色虛線)時波前走時(圖12)。可見兩種方法計算的波前走時趨勢基本一致，反映出遇到低速體、高速體和地層界面時的波前變化特征。相比LTI方法，LTPI方法在網格距增大時走時變化更小，穩定性更高。

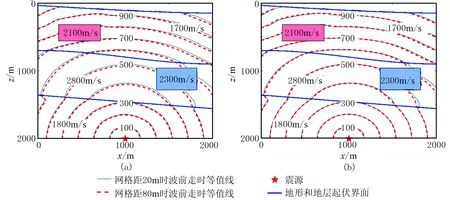
圖12 離散網格距分別為20m和80m時模型4波前走時等值線(單位ms)圖(a)LTI方法波前走時； (b)LTPI方法波前走時

將模型4分別用20m和80m的網格距離散，并分別使用LTI和LTPI方法計算射線路徑(圖13)。可見LTI和LTPI兩種方法計算的射線路徑都表現出盡量避開低速體和趨向高速體的特征。但是，當模型離散網格距發生變化時，LTI方法計算的射線路徑變化較大，而LTPI方法計算得到的射線路徑更為合理且變化更小，反映出LTPI方法更具優勢。

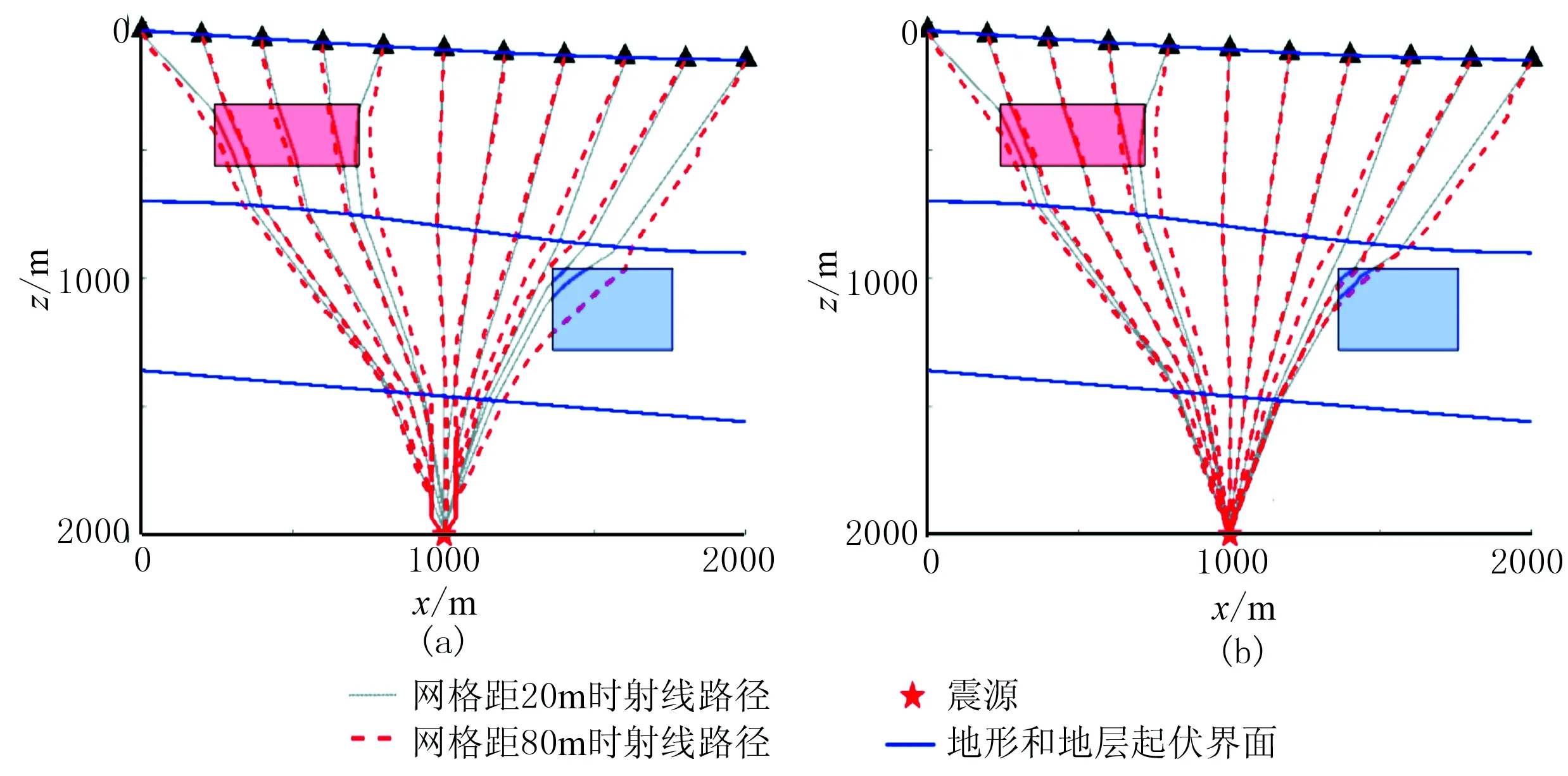
圖13 模型4射線路徑圖(a)LTI方法； (b)LTPI方法

4 結論

線性走時擾動插值(LTPI)方法將實際波前走時分解為等效勻速介質中的參考走時與走時擾動。參考走時沿單元邊界非線性變化，雖然假設走時擾動在單元邊界上線性變化，但與參考走時相比，走時擾動很小。因此，參考走時與走時擾動之和仍保持著沿單元邊界非線性變化的特征，從而克服了常用的線性走時插值(LTI)方法在離散單元較大時計算走時誤差大的問題，提高了波前走時的計算精度。

采用不規則單元離散復雜介質模型，能夠更好地模擬地形和地層界面的起伏形態以及各地層內速度的縱橫向變化。針對不規則單元，建立了基于LTPI的走時計算方程，并結合GMM波前擴展算法，提出了一種基于線性走時擾動插值的射線追蹤方法，對復雜介質模型具有很強的適應性。

不同模型的測試結果表明， 相比LTI方法，LTPI方法在波前走時和射線路徑方面具有更高的計算精度，并且隨著離散模型單元尺寸的增加，LTPI方法的計算誤差增加更為緩慢。在離散單元數目相同的情況下，LTPI與LTI方法的計算效率相當，但LTPI的計算精度比LTI方法高出一倍以上；在一定精度要求下，LTPI方法可使用離散單元數目更少的模型，從而提高計算效率。