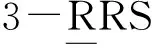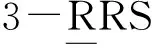計及重力的并聯機構靜剛度分析

汪滿新 諶秋生 祖 莉 劉海濤

(1.南京理工大學機械工程學院， 南京 210094; 2.天津大學機構理論與裝備設計教育部重點實驗室， 天津 300072)

0 引言

并聯機構因具有剛度大、結構穩定、承載能力強、精度高、運動慣性小、實時控制性好等特點而得到廣泛應用[1]，特別是1T2R 3自由度并聯機構[2-6]，如Z3主軸頭中3-PRS并聯機構[3]，Tricept、Exechon以及TriVariant等混聯機器人中的3自由度并聯模塊[4-6]，已在飛機大部件加工與自動鉆鉚、機身與機翼對接面現場加工、汽車發動機缸體銷孔過盈裝配以及大型鋼結構相貫線切割等方面得到應用。

靜剛度可表征機構在外載荷作用下抵抗變形的能力，是并聯機構最重要的性能之一，因而常常被作為評價機構性能以及機構結構參數優化設計的指標。基于剛度優化設計的先決條件是構建精確的剛度模型。有限元法[7-8]、解析/半解析法[9-11]是目前剛度建模常用的兩類方法。有限元法建模精度高，但僅能在指定位形下劃分網格計算，無法預估機構全域剛度的變化規律，故多適用于校核最終設計。考慮到機構剛度隨位形變化的特點，解析/半解析法是預估機構全域剛度的有效方法。在解析法建模方面，GOSSELIN[12]基于虛功原理提出了虛鉸鏈法，該方法用一維彈簧來等效模擬機構主動關節彈性變形，建立了力與末端變形的映射模型；PASHKEVICH等[13-14]將假想彈簧擴充到6維，以一類過約束并聯機構為對象構建了計及被動關節彈性變形的剛度模型。為有效分離驅動剛度和約束剛度對機構末端剛度的貢獻，許多學者利用旋量理論構造出全雅可比矩陣或廣義雅可比矩陣用于并聯機構的剛度建模中[15-21]，文獻[15-16]利用上述方法分別建立了3-PUU、3-RPS并聯機構的靜剛度模型。此外，落海偉等[17]提出了一種基于子結構綜合和靜態凝聚技術的靜剛度建模方法，并綜合考慮了鉸鏈和支鏈彈性對靜剛度的貢獻。

值得指出，傳統的解析/半解析剛度建模大多未考慮重力場的影響，但實際中重力因會引起構件發生彈性變形而影響機構末端精度。文獻[18-19]研究重力場剛度建模問題時將重力等效為集中力，這僅適用于將連桿視為剛體的場合。文獻[20-21]基于變形協調條件研究了重力對過約束機構受力的影響。文獻[22-23]計及了運動部件分布重力的影響，并考慮了各構件/鉸鏈的柔度分別構造了3-SPR及3-RPS并聯機構的靜柔度模型，所建模型建立了零部件彈性和重力與末端變形之間的映射關系，進而為有針對性改進設計提供了一種有效手段。

1 系統簡介與位置逆解

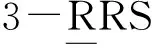
圖三維模型Fig.1 3D model of parallel mechanism1.機架 2.轉動副從動臂 4.球副S 5.動平臺 6.主動臂 7.轉動副R

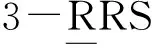
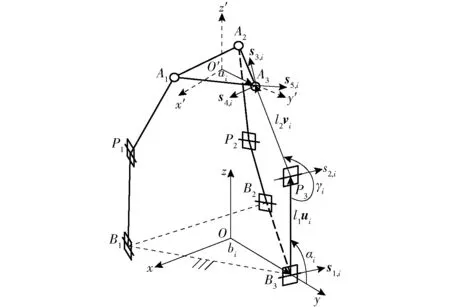
圖并聯機構結構簡圖Fig.2 Schematic diagram of parallel manipulator

系{R′}相對于系{R}姿態矩陣R可根據z-x-z旋轉變換，用進動角ψ、章動角θ與自旋角φ表示為

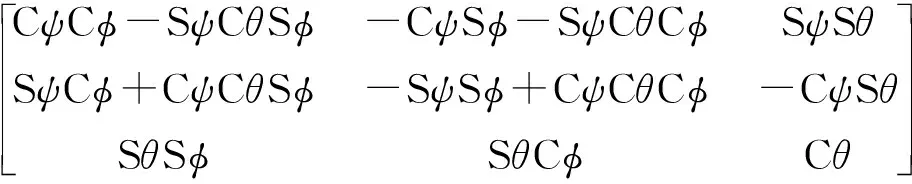
(1)

式中，S表示sin，C表示cos。

將球副看成由軸線相交于一點的3個轉動副串聯組成，并令sj,i表示支鏈i中第j個運動副的單位矢量，由關節軸線間關系可得約束s1,i∥s2,i，s2,i⊥s3,i，s3,i⊥s5,i，s5,i⊥s4,i(i=1,2,3)。

此外，為了描述各構件的姿態，建立如圖3所示連體參考坐標系{Rj,i}(i=1,2,3;j=1,2,3)。

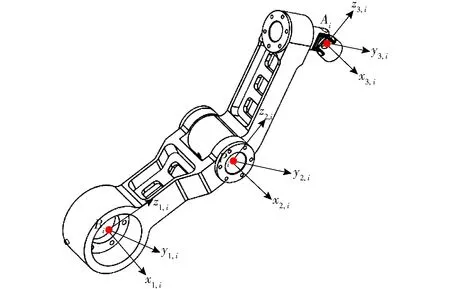
圖3 各構件連體坐標系Fig.3 Body fixed frames of each components

(1) {R1,i}為主動臂連體坐標系，以Bi點為原點，軸z1,i方向由Bi指向Pi，軸x1,i與s1,i重合。

(2) {R2,i}為從動臂連體坐標系，以Pi點為原點，軸z2,i方向由Pi指向Ai，軸x2,i與s2,i重合。

(3) {R3,i}以Ai為原點，且與系{R2,i}相平行。

r=bi+l1ui+l2vi-ai(i=1,2,3)

(2)

式中bi——由點O到Bi的位置矢量

ai——由點O′到Ai的位置矢量

ui——由點Bi到Pi的位置矢量

vi——由點Pi到Ai的位置矢量

其中

bi=bsiai0=asiai=Rai0

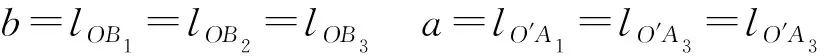
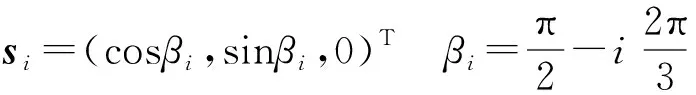
式中αi——BiPi相對于OBi的轉角

βi——OBi相對于x軸的轉角

注意到s1,i⊥bi，s1,i⊥ui，s1,i⊥vi，對式(2)兩端同時點乘s1,i，可得

(r+ai)Ts1,i=0 (i=1,2,3)

(3)

其中

s1,i=(-sinβi，cosβi，0)T

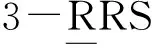
(4)

至此，可通過式(4)解出參數(x，y，φ)，從而可解出R、r和ai。由式(2)可得

(5)

其中

展開式(5)可得

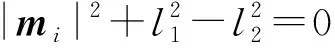
(6)

求解式(6)可得

(7)

其中

Bi=-2l1mixcosβi-2l1miysinβi

Mi可依據機構初始位型唯一確定，從而可進一步求出ui及

(8)

2 靜剛度建模

注意到動、靜平臺的剛性遠大于支鏈體各部件的剛性，故可作剛體處理，此外，在建模過程中，將計及支鏈體各部件彈性及所有運動部件的重力。

2.1 力分析

力分析目的在于建立末端動平臺上的外載荷及運動部件重力與關節反力間的映射關系。如圖4所示為末端動平臺受力示意圖，通過對點O′取矩，可建立平衡方程

f-mg
τ-(lmR)(-mg

(9)

其中

ni=vis1,i=(0，0，1)T

式中f、τ——外力和外力矩

m——動平臺質量

lm——點O′到動平臺質心的距離

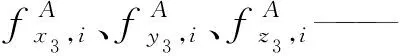
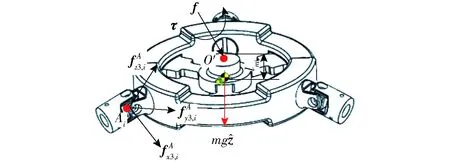
圖4 動平臺受力圖Fig.4 Free body diagram of moving platform

顯見，式(9)所要求解未知數個數為9但獨立方程個數僅為6，無法求解，為解決該問題，以圖5所示從動臂為研究對象作力分析，對點Pi取矩可得靜力平衡方程

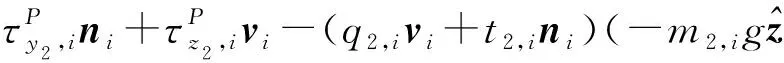
(10)

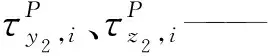
m2,i——從動臂質量

q2,i(t2,i)——從動臂重心到點Pi的位置矢量沿vi(ni)方向的投影對式(10)兩端同時點積s2,i，得

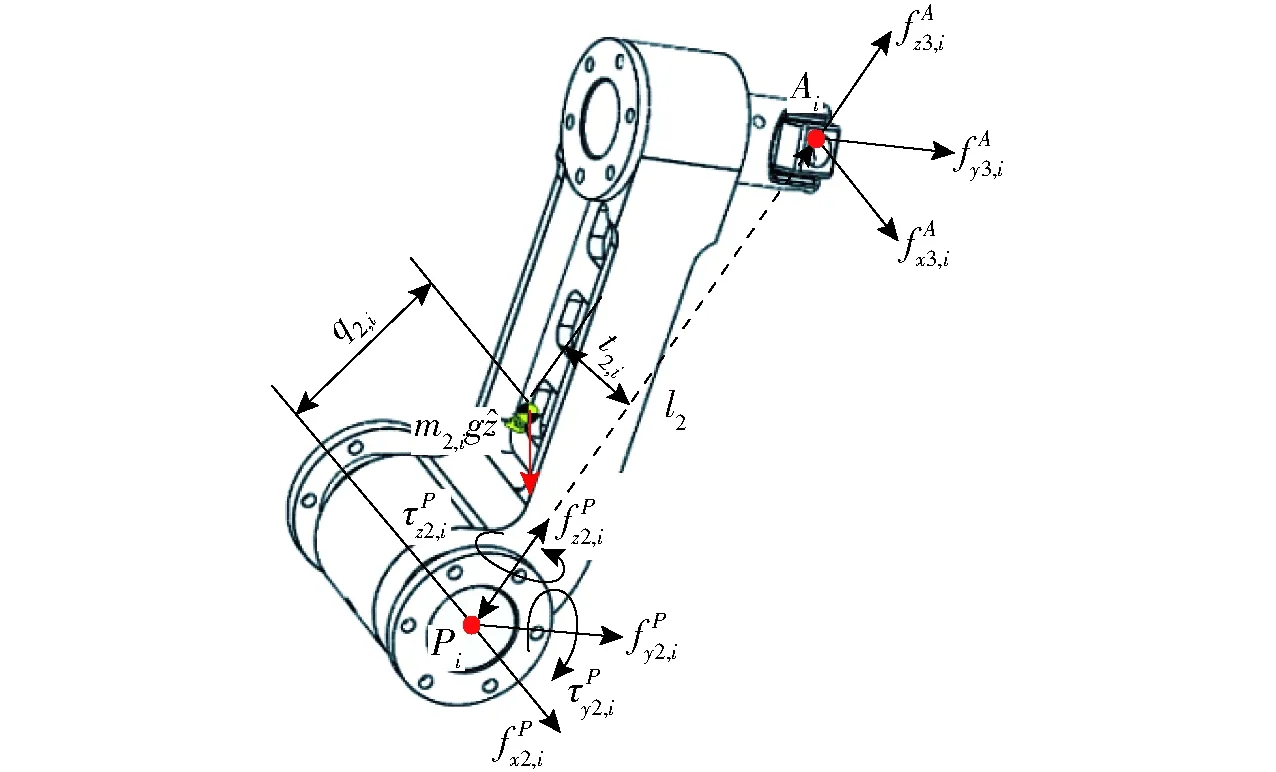
圖5 從動臂受力圖Fig.5 Free body diagram of driven link

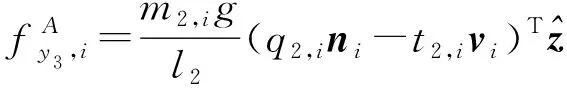
(11)

將式(11)代入式(9)并寫成矩陣形式，得

(12)

其中

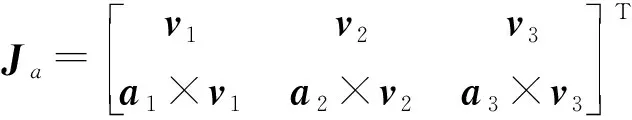
式中J——機構的廣義雅可比矩陣[24]

Ja、Jc——驅動和約束雅可比矩陣

ρw——界面力矢量

ρwa、ρwc——界面驅動和約束力矢量

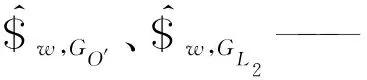
故式(12)表示的物理意義為：施加在動平臺上的等效外載荷應由作用在其上的所有支鏈界面驅動力和界面約束力共同承擔。

2.2 變形分析

(13)

式中 δrO′、δαO′——末端參考點O′的線變形矢量、動平臺的角變形矢量

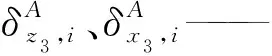
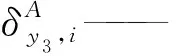
對式(13)兩端分別點乘vi和s1,i，得

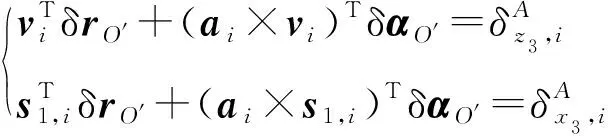
(i=1,2,3)

(14)

將式(14)改寫成矩陣形式，得

(15)

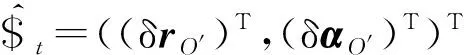
式中ρt——關節變形量

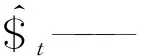
ρta、ρtc——沿驅動、約束方向的關節變形量

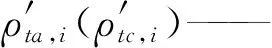
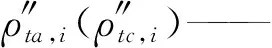
(16)

其中

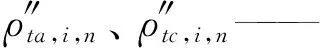
2.3 靜剛度建模

(17)

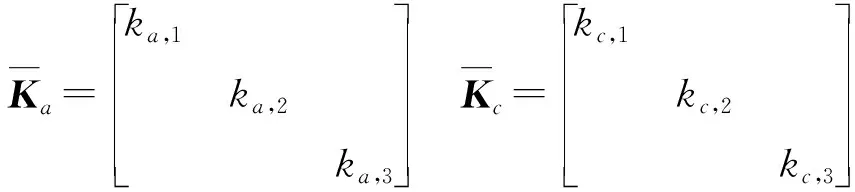
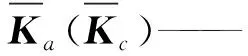
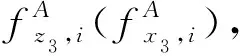
(18)

其中

(19)

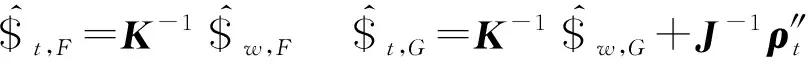
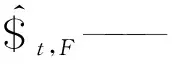
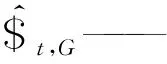
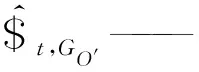
2.4 構造和

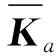
(20)

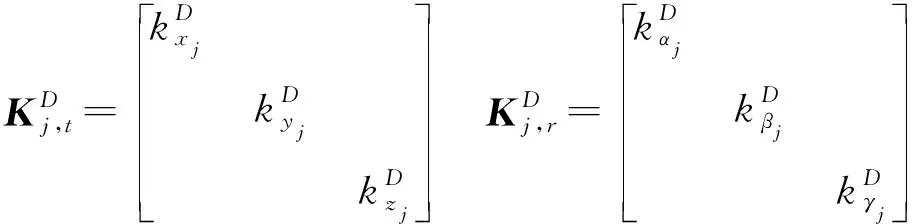
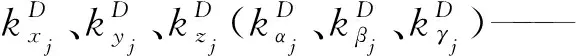
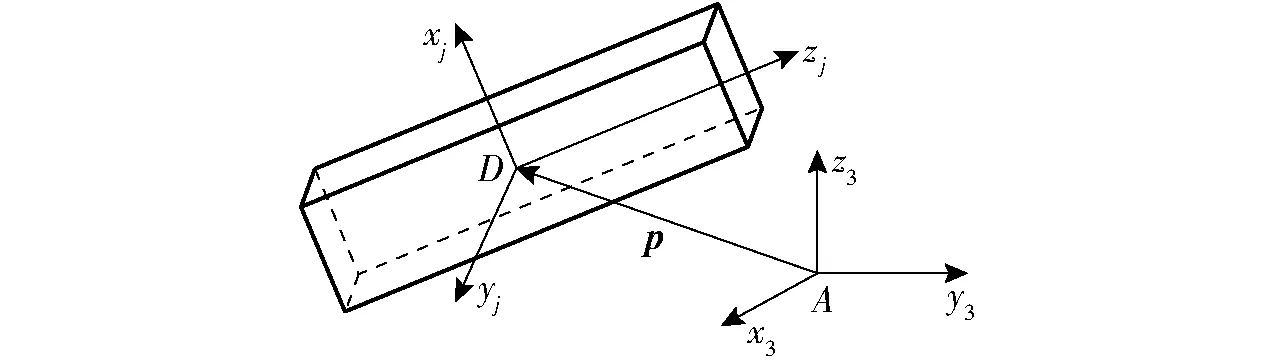
圖6 用于剛度矩陣評估和變換的連桿示意圖Fig.6 Link model for stiffness evaluation and transformation

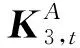
(21)

其中

式中R3,j——系{Rj}相對于系{R3}的姿態矩陣

p——由點A指向點D的位置矢量(圖6)

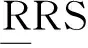
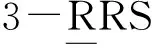
(22)

式中，0表示除約束與驅動方向外存在微小位移，是3條支鏈與同一個動平臺相連接所需的兼容性條件。

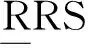
(23)

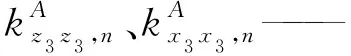
對于子裝配體1，應用式(21)，其剛度可表示為

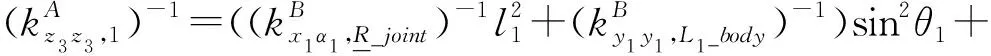
(24)

式中θ1——ui與vi的夾角

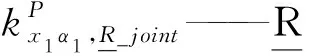
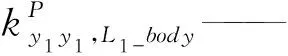
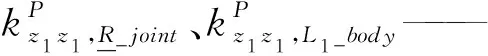
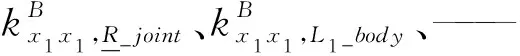
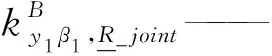
對于子裝配體2，應用式(21)得

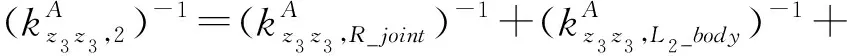
(25)

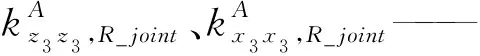
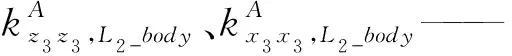
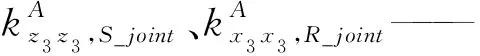
由于S副尺度參數比較小，變化幅度不大，故為簡化計算，將其視為常數。

2.5 構造和

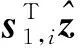
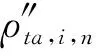
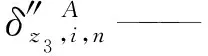
對于子裝配體2，在工作空間范圍內，vi與的夾角θ2接近于0，故很小，可忽略不計。因此，只需考慮其可表示為

(26)

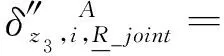
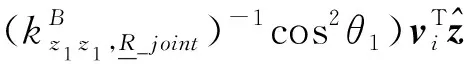
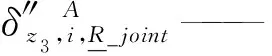
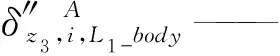
3 算例

本節利用前述推導出的模型，研究末端靜剛度和運動部件重力所引起的末端變形的分布規律以及各構件剛度和重力對末端靜剛度和變形的影響。表1～4分別示出了機構的尺度參數、各部件的剛度系數、質量及其質心參數,以上數據來源于機構的三維模型、有限元軟件及相關設計手冊。

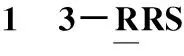
表并聯機構尺度參數與工作空間Tab.1 Dimensions and workspace of parallel mechanism

表2 支鏈體各部件的質量、質心位置及動平臺質量Tab.2 Masses and their locations of platform and limb-body assembly

表3 子裝配體1在其局部坐標系下的剛度系數Tab.3 Stiffness coefficients of the first sub-assembly evaluated in body fixed frames

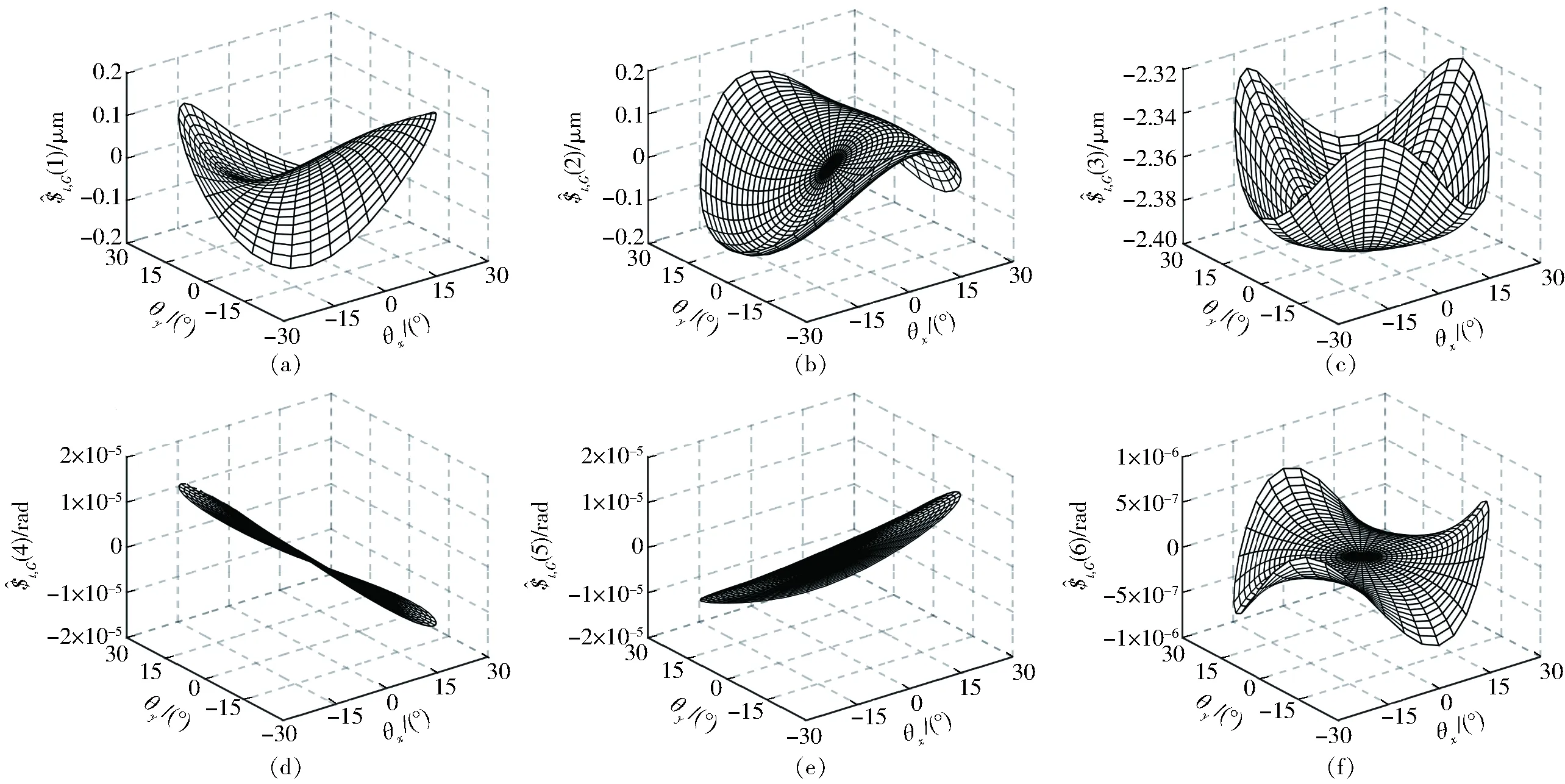
圖7 z=150 mm時分布規律Fig.7 Distributions of when z=150 mm

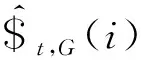
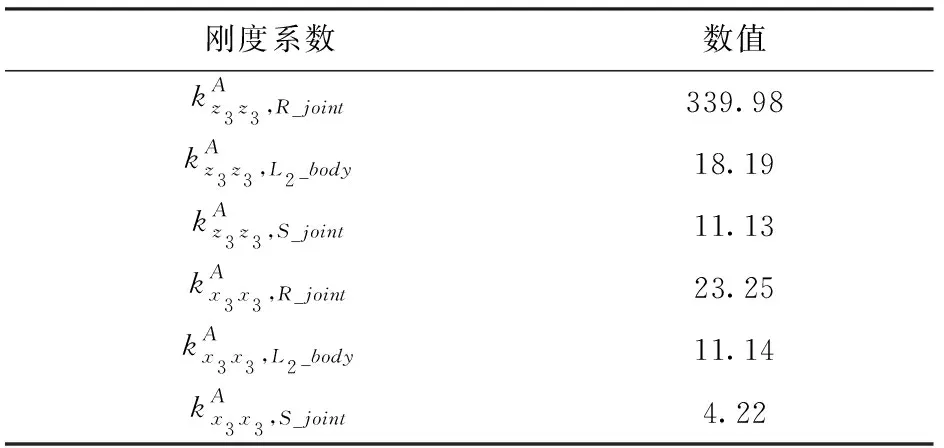
表4 子裝配體2在其局部坐標系下的剛度系數Tab.4 Stiffness coefficients of the second sub-assembly evaluated in body fixed frames N/μm

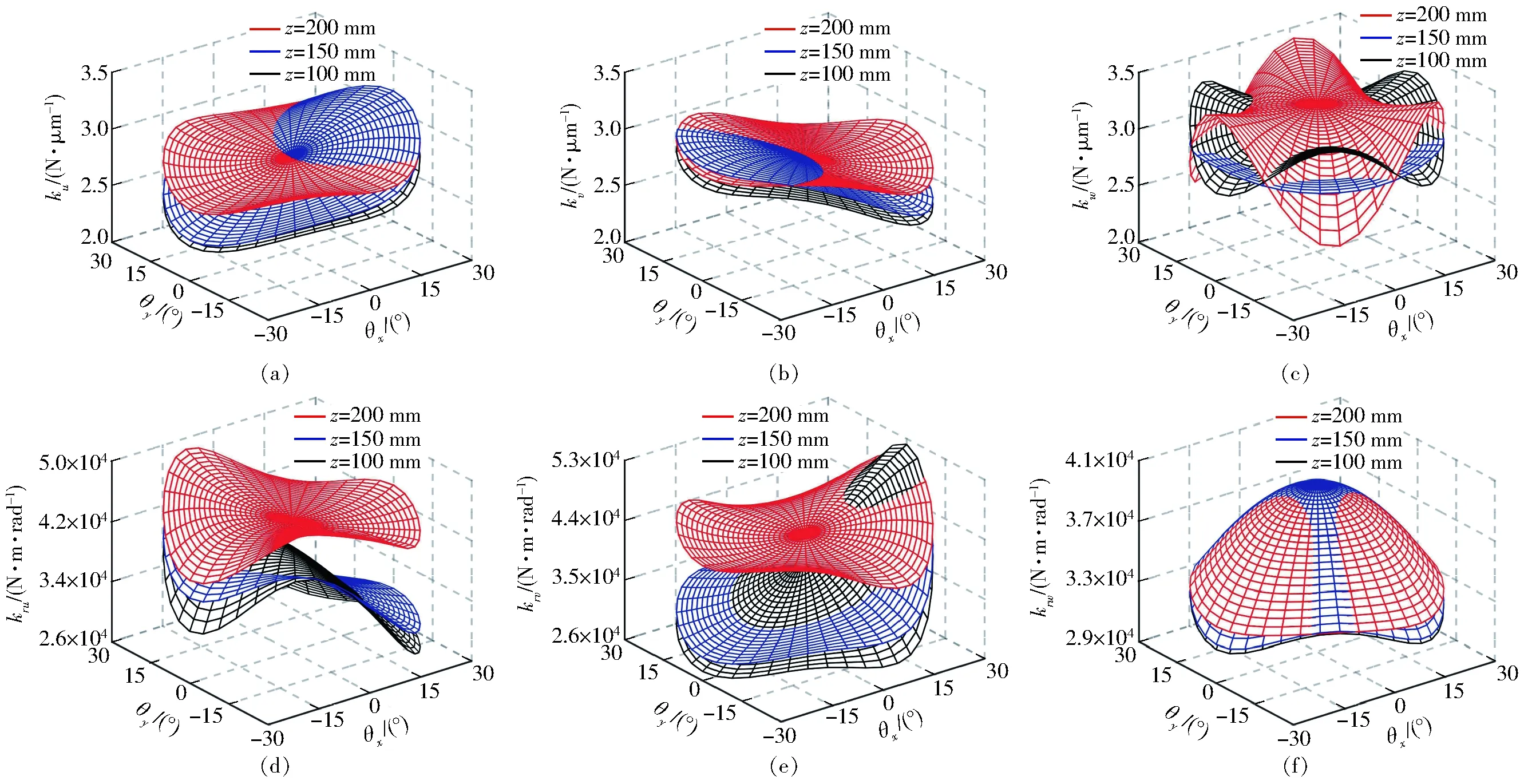
圖8 末端剛度全域分布規律Fig.8 Stiffness distributions within entire workspace

為評估驅動(約束)剛度及各部件剛度對末端靜剛度的貢獻，定義全域靜剛度性能評價指標為

(27)

式中Wt——給定全域工作空間體積

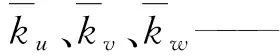
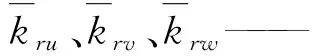
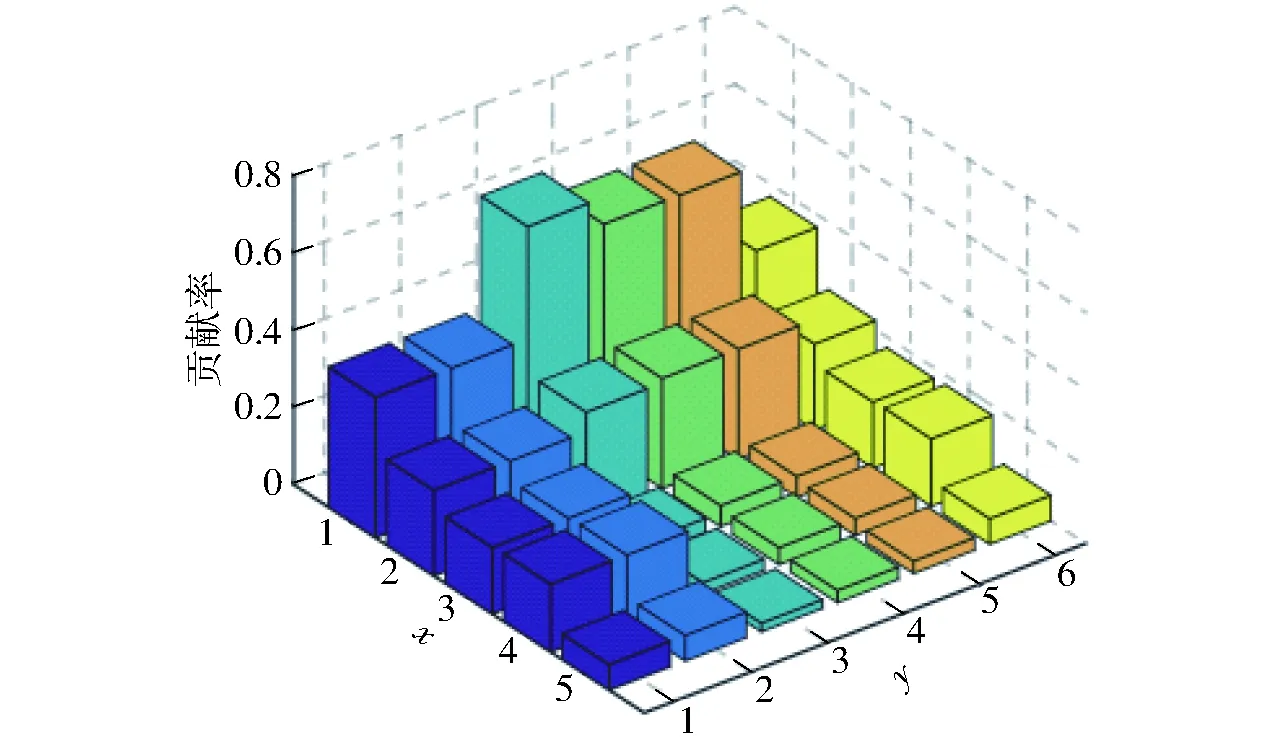
圖9 各構件剛度對末端剛度的貢獻率Fig.9 Contributions of component stiffness to stiffness of platform

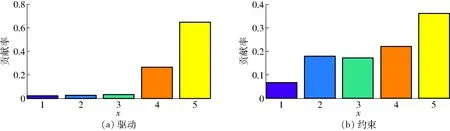
圖10 各構件剛度對界面剛度的貢獻率Fig.10 Contributions of component stiffness to interface stiffness

圖11 各部件重力對末端變形量的貢獻率Fig.11 Contributions of gravity to global deflection

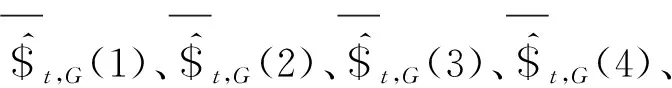
向產生變形，因而為了減少主動臂的重力對末端變形的影響，可適當增加支鏈驅動方向的剛度。

為了驗證所建模型的正確性，利用ANSYS軟件，計算末端點位于z=150 mm，θ=30°時的靜剛度及重力引起的末端變形量。值得指出，該位形下沿x方向的線變形以及繞x、y、z方向的角變形量近似為零，故在此僅計算沿y、z坐標軸方向的靜剛度及線變形量。同時，在有限元軟件中設置的邊界條件與文中的理論分析方法相同，以保證兩種方法具有可比性。圖12給出了末端參考點在上述位形且受單位力作用下機構沿y、z軸方向的變形云圖。圖13則給出了機構在該位型時在重力作用下沿y、z軸方向的變形云圖。表5給出了半解析法與有限元軟件的計算結果。由表5可見，有限元軟件求解結果絕對值略小于半解析法求解結果的絕對值，但二者的取值非常接近，進而驗證了半解析法是正確有效的。

圖12 z=150 mm、θ=30°時受單位力作用下沿y、z方向變形量Fig.12 Deflections along y and z axis arising from unit force when z=150 mm and θ=30°

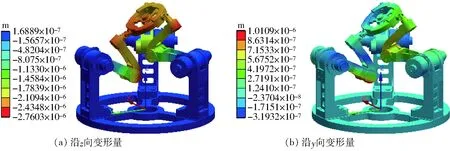
圖13 z=150 mm、θ=30°時重力作用下沿y、z方向變形量Fig.13 Deflections along y and z axis arising from gravity when z=150 mm and θ=30°

方法$^t,G(2)/μm$^t,G(3)/μmkv/(N·μm-1)kw/(N·μm-1)半解析法-0.1195-2.3663.00812.592有限元法-0.1153-2.3462.83212.425

4 結論

(2)所建末端變形模型可有效分離零部件彈性和重力對末端變形的影響，進而可為指導詳細結構設計提供重要的理論依據。