旋轉電機穩態分析的通用方法

，

(哈爾濱大電機研究所，黑龍江哈爾濱150040)

0 引言

旋轉電機穩態分析是電機學的基礎內容。傳統的分析方法是將各類電機分別進行研究，各類電機都有自己獨特的分析系統。例如，對于異步電機，就有T型等效電路分析法、圓圖分析法等完備的分析系統，可對異步電機的穩態特性進行有效的分析。這是學者們歷經多年做出的卓越貢獻。可是，異步電機傳統的等效電路與別的電機，例如同步電機，直流電機的有很大差別，相互不能通用。

隨著經濟與科技的發展，旋轉電機在國計民生中的應用越來越廣泛，而且，出現了一些新的應用情況。為了便于理解和應用，我們試圖從理論上來探討，尋求一種對于各類電機都適用的穩態分析方法，以便能比較直觀地分析各類電機的穩態性能。

通過對旋轉電機本質特征的分析，根據機電能量轉換過程的原理和旋轉電機定、轉子電路的耦合關系，可以得出一種旋轉電機穩態分析通用的電路模型。其最完備的電路對應于雙饋電機；其它各類電機電路模型都可由雙饋電機電路模型簡化而得。

這一通用分析方法的基本思想是在定、轉子之間耦合關系的前提下，將電機實際的定子回路和轉子回路分開來分析，并且使之適合于各種類型的旋轉電機。

1 旋轉電機的基本特征

旋轉電機是一種機電能量轉換裝置；而任何一種機電能量轉換裝置都是由電系統、機械系統和用作耦合、貯藏能量的電磁場(耦合場)所組成；都有一個固定部分(定子)和一個可動部分(轉子)。

機電能量轉換過程是電磁場與可動的載流體相互作用的結果。即可動載流體的位移引起磁場能量變化，從而產生電磁力，使部分磁場儲能釋放出來，變為機械能；同時，磁鏈變化引起的磁能變化將通過載流體內的運動電勢，從電源輸入等量的電能，而不斷得到補充。這樣，通過耦合場-氣隙磁場的作用，電能與機械能不斷地轉換。

由此可見，機電能量轉換的關鍵在于運動電勢和電磁轉矩的產生；而它們都是通過耦合場—氣隙磁場的作用實現的。各類電機電路模型都由雙饋電機電路模型簡化而得，各電機電路圖如圖1，圖2，圖3，圖4所示。

圖1 雙饋電機

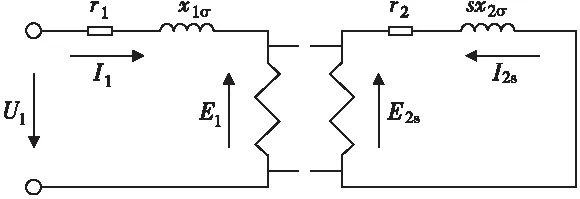
圖2 異步電機

圖3 同步電機

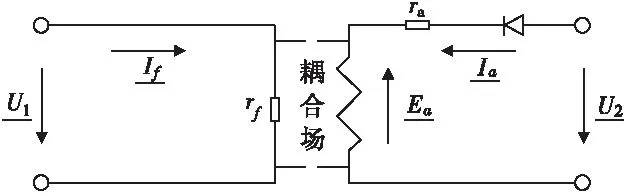
圖4 直流電機

所以，建立旋轉電機通用電路模型的關鍵在于如何根據各類電機的特點，正確反映定、轉子回路中運動電勢和電磁轉矩。

實際上，旋轉電機通常都有兩個繞組，定子和轉子上各有一套繞組。轉子繞組主要用以產生主磁通，并形成主磁極。定子繞組是主要的載流體，定子繞組對轉子繞組有相對運動。由于包括主磁通在內的合成磁通的變化，定子繞組中會連續產生運動電勢。當定子繞組中流過電流時，定子繞組與氣隙磁場相互作用而產生電磁轉矩。這便是旋轉電機共同的機理。

通過以上分析，我們不難看出：盡管旋轉電機有多種類型，但是，就其本質而言，它們都是由具有相對運動的若干電磁耦合繞組所組成，應該存在著建立穩態分析通用電路模型的可能性。

2 旋轉電機的穩態性能

穩態性能是各類旋轉電機的基本性能，是最常用的電機性能。電機的穩態性能可以用電機的基本方程，集中參數電路和相量圖來描述。

基本方程即電機各回路的電壓方程，其中包含了電路的各個參量。集中參數電路能反映電機內部的電磁和機電關系，可用以計算電機的穩態特性。電機相量圖則可用以表示電機各回路主要物理量之間的相位關系。集中參數電路是分析電機穩態性能的主要工具。其余兩種方法可以由它導出。因此準確構建電機的集中參數電路特別重要。

如上所述，旋轉電機都有定子和轉子兩個部分；而且，它們之間存在耦合關系，形成一個完整的機電能量轉換系統。集中參數電路應能準確反映電機內部的電磁和機電過程，反映電機定、轉子回路中的運動電勢和電磁轉矩的形成機制。所以，在構建電機的集中參數電路時應特別注意以下兩點。

(1)考慮定、轉子耦合關系后，確定電機定、轉子回路中各自的運動電勢；

(2)準確考慮定、轉子回路中,由于導體運動對電路參數造成的影響。

實際上，就是要考慮各回路的運動電勢對磁場變化和線圈匝數的關系，以及各回路參數與電流頻率的關系，也就是要準確給出實際的定子回路和轉子回路的參數。這樣，就不再需要先將轉子電路歸算到定子電路側；而只要對實際的定子回路和轉子回路分別進行計算。對應各類電機不同的電路，可以直接計算出定子和轉子回路的實際參數。

這就是本文所提旋轉電機穩態分析通用方法的原理。

3 電動機的穩態分析

如上所述，從各類旋轉電機的共性出發，依照描述電機穩態特性的一般方法，可以引出旋轉電機穩態分析的通用方法。即在計及定、轉子通過磁場耦合的前提下，對電機實際的定子回路和轉子回路分別進行計算。需要注意的是這里的轉子回路處于旋轉狀態，而非靜止狀態。

這一方法適用于各種類型的旋轉電機。以下，分別對旋轉電機的幾種主要類型進行討論。

假設：電機定、轉子相數分別為m1和m2

電機定、轉子有效匝數比為

電機的轉差率為

式中，w1—定子每相串聯匝數；w2—轉子每相串聯匝數；kw1—定子繞組系數；kw2—轉子繞組系數；f1、f2—定、轉子的電頻率。

并假定各類電機均以電動狀態為例進行討論。

3.1 雙饋電機

雙饋電機是一種定轉子均參與機電能量轉換的旋轉電機[1、2]，近年來在新能源和變速系統中得到廣泛應用。

3.1.1 集中參數電路

以下用黑體字表示電路各參數的相量。

雙饋電機的集中參數電路是所有電機中最完備的，參數最全，可以涵蓋其他幾種電機的情況，如圖1所示。其中

定子電勢

E1=-j4.44f1w1kw1Φm

轉子電勢

E2s=-j4.44sf1w2kw2Φm=E1s/k

式中，Φm—主磁通相量。定、轉子電源的頻率需滿足機電能量轉換條件的約束[1]。

3.1.2 基本方程

根據基爾霍夫定律，可以分別得到定轉子回路電壓方程。

定子回路

U1=I1(r1+jx1σ)-E1

轉子回路

U2=I2s(r2+jsx2σ)-E2s

式中，x1σ、x2σ—定子、轉子的靜態漏抗。

從上面兩式可以得出

定子電流

I1=(U1+E1)/(r1+jx1σ)

轉子電流

I2s=(U2+E2s)/(r2+jsx2σ)

定子輸入電功率

P1=Re(m1U1I1*)=m1U1I1cosφ1；(I*為I的共軛相量)

電磁功率

Pm=Re(m1E1I1*)=m1(U1I1cosφ1-I12r1)

轉子輸入電功率

P2=Re(m2U2I1s*)

=m2U2I2scosφ2

=Re(m2E2sI2s*)+m2I2s2r2

轉子繞組傳遞功率

Pe2=Re(m2E2sI2s*)

≈sRe(m1E1I1*)=sPm

轉子銅耗

Pcu2=m2I2s2r2

機械功率

Pmech=Pm-Pe2=(1-s)Pm

3.1.3 相量圖

相量圖表示電機定轉子回路中電壓、電流等相量之間的相位關系，雙饋電機的相量圖如圖5，圖中右側是轉子的電壓相量圖；中間是電流(磁動勢)相量圖；左側為定子電壓相量圖。

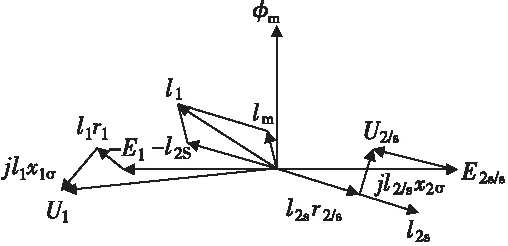
圖5 雙饋電機相量圖

3.2 異步電機

3.2.1 集中參數電路

異步電機的定、轉子回路電勢與雙饋電機相同，但轉子回路是短接的；沒有連接電源。所以得出異步電機的定轉子電路。

3.2.2 基本方程

定子回路

U1=I1(r1+jx1σ)-E1

轉子回路

o=I2s(r2+jsx2σ)-E2s

即

o=I2s(r2/s+jx2σ)-E2s/s

可算得

I1=(U1+E1)/(r1+jx1σ)

I2s=E2s/(r2+jsx2σ)

定子輸入功率

P1=m1U1I1cosφ1

電磁功率

Pm=Re(m1E1I1*)=m1(U1I1cosφ1-I12r1)

從轉子側看,

電磁功率

Pm=m2Re(E2s/sI2s*)

=m2E2sI2scosφ2/s

=m2I2s2r2/s

轉子銅耗

Pcu2=m2I2s2r2

機械功率

3.2.3 相量圖

對應于定轉子回路的基本方程，可得到異步電機的相量圖如圖6。

圖6 異步電機相量圖

3.3 同步電機(以隱極電機為例)

同步電機轉子以同步轉速旋轉。可以把它看成為雙饋電機的一種特定運行方式。它的定、轉子也都有電能流入，定子通交流電，轉子中則為直流電。

同步電機定子的電動勢E1由主極磁動勢和電樞反應磁動勢共同產生，即

E1=E0+Ea

式中，E0—激磁電動勢；Ea—電樞反應電動勢，Ea可看成是電抗壓降的負值，即

Ea=-jI1xa

式中，xa—電樞反應電抗。

3.3.1 集中參數電路

如上所述，同步電機定子回路為交流電路，其感應電勢E1為激磁電勢E0與電樞反應電勢Ea之和；轉子回路為直流回路。

3.3.2 基本方程

根據前面的說明，可得同步電機的基本方程如下

定子回路

U1=I1(r1+jx1σ)-E1

或

U1=I1(r1+jx1σ)+jxa)-E0

轉子回路

U2=I2r2

以下分別記電機的鐵耗和機械耗為PFe,PΩ。

可以計算出

定子輸入功率

P1=m1U1I1cosφ1

電磁功率

Pm=m1U1I1cosφ1-m1I12r1

機械功率

Pmech=Pm-PFe-PΩ

轉子銅耗

Pcu2=m2I22r2

3.3.3 相量圖

在不計飽和前提下，根據基本方程可得同步電機的相量圖如圖7。

圖7 同步電機相量圖

3.4 直流電機

3.4.1 集中參數電路

典型直流電機的定子為直流激磁回路。轉子(電樞)回路內部為交流電路，經整流后變為直流，所以其集中參數電路可以用圖4表示。

其中，電樞的感應電勢

Ea=4Nfφm=4Npnφm/60=Cenφm

式中，N—電樞繞組串聯匝數；n=60f/p；p—極對數。

3.4.2 基本方程

勵磁回路

U1=Ifrf

電樞回路

U2=Ua=IaRa+Ea

可以算得

勵磁回路輸入

Pf=UfIf=If2rf

電樞回路輸入

Pa=UaIa=Ia2ra+EaIa

電磁功率

Pm=EaIa

機械功率

Pmech=Pm-P0=Pm-(PΩ+PFe+Pd)

式中，P0—空載損耗；Pd—附加損耗。

對于直流電機，相量圖不再有意義。

這一節按照常用的電機穩態特性的描述方法，利用本文提出的由實際的定子和轉子參數構成的集中參數電路可以比較直觀地計算各類電機的穩態特性，說明了這種穩態分析方法的可行性和通用性。

4 結語

為了便于理解各類旋轉電機的穩態性能，本文提出了一種旋轉電機穩態分析通用方法的設想。旋轉電機機電能量轉換的機理是這一通用分析方法的基礎，并使這一方法有可能適用于各類旋轉電機。這一方法以雙饋電機為分析母本，其它電機均可按照由它蛻化所得的電路進行分析。這是該方法的一個特點。

這一方法直接對各類電機的定子電路和轉子電路分別進行分析計算，從而得到定、轉子回路實際物理參數，就可對各類電機的穩態性能進行分析。但本文是對這一方法的初步探討。這一方法的實用性、局限性等問題尚有待于進一步深入研究。