應急車輛分配與應急物資配送的集成決策

王莉，周鮮成，趙志學，劉利枚，余伶俐

?

應急車輛分配與應急物資配送的集成決策

王莉1，周鮮成2，趙志學1，劉利枚1，余伶俐3

(1. 湖南商學院 計算機與信息工程學院，湖南 長沙，410025；2. 湖南商學院 湖南省移動電子商務協同創新中心，湖南 長沙，410025；3. 中南大學 信息科學與工程學院，湖南 長沙，410083)

針對應急物資配送中各受災點應急車輛分配的公平性與應急物資配送的及時性難以平衡的問題，以各受災點車輛分配的相對剝奪感(公平性)與配送時間(及時性)為目標函數，構建基于車輛分配公平性與應急物資配送及時性的多目標協調優化模型。為求解該模型，設計一種基于啟發式算法、局部搜索算法和遺傳算法的混合智能算法。研究結果表明：當配送中心車輛數不足時，公平性和及時性之間存在關聯；該混合智能算法能快速、有效地找到滿意解；目標權重對算法的穩定性和快速性有一定影響；該模型和算法在大規模地震實例中能有效實現公平性與及時性的協調優化。

應急物資配送；相對剝奪感；公平性；及時性；協調優化

自進入21世紀以來，全球自然災害頻發，給人民群眾造成了巨大的生命財產損失。由于各個受災點的受災情況和地理位置不同，受災群眾對救援物資的需求以及物資運達時間的期望也不同。為了第一時間滿足受災群眾的基本物資需要，安撫各受災點群眾，制定出科學、合理的方案，以提高車輛分配的公平性與物資配送的及時性是非常必要的。目前，國內外關于應急物資配送的公平性研究主要針對物資分配，追求的是物資需求滿足的最大化或者公平損失的最小化。馬衛峰等[1]建立了以物資分配量最大和最小滿意度的多目標數學模型，實現救災物資在災區的合理、公平分配。CHANTA等[2]以基尼系數公平性指標建立了多目標規劃模型，采用鄰域搜索算法求解。馮春等[3]以各周期懲罰成本最小化建立了多周期應急物資配送的公平性模型，采用混合整數線性規劃算法求解。張錦等[4]建立了基于變權的資源分配公平性模型，以效率損失和公平損失最小為目標，分析了變權參數對公平的影響。BEHESHTI等[5]建立了以顧客滿意度最大化為優化目標的數學模型，并采用量子進化算法進行求解。胡志華等[6]基于相對剝奪理論對應急物資車輛分配的公平性進行建模，利用橫向和縱向相對剝奪感評價車輛分配的公平性，并采用啟發式算法求解。在應急物資配送及時性研究方面，國內外學者以配送時間最小或延遲懲罰最小為目標，建立了規劃模型或優化模型，并采用不同的算法求解。王海軍等[7]建立了混合整數規劃模型，并采用基于非支配解排序的遺傳算法求解。劉長石等[8]構建了1個基于機會約束規劃的多目標模糊LRP優化模型，并采用混合免疫遺傳算法求解。ZHOU等[9]建立了多目標優化模型，采用基于分解的進化算法求解。OTHMAN等[10]建立了單一供應商多客戶模式的應急物資調度決策系統，采用分支定界算法求解。目前，國內外關于應急物資配送公平性與及時性的協調優化也進行了研究，如BEHESHTI等[5]提出了1個基于時間最短以及公平性最大的多目標優化模型，并運用多目標量子遺傳算法求解。鄭斌等[11]建立了應急物資配送雙層優化模型，上層以物資配送時間最短、下層以物資分配公平性最大為目標，并采用混合遺傳算法求解。在此基礎上，鄭斌等[12]考慮物資最低滿足率限制等其他約束條件，建立了雙層規劃動態模型。陳瑩珍等[13]建立了1個雙目標優化模型，其目標函數是最大化地區的物資滿足量以及最小化最大配送時間，采用差分進化算法求解。國內外學者關于應急物資配送中的公平性、及時性以及兩者的協調優化方面進行了研究，取得了一些成果，但還存在以下幾個問題：1) 大多數研究了物資需求是否得到滿足問題，很少討論配送車輛的分配是否公平問題。實際上，車輛分配的公平性會直接影響物資需求的滿意度，前者是因，后者是果，若車輛分配不公平，則滿意度也會大大降低。2) 公平性模型中大多通過改變公平性指標或者權重尋求公平性的最大化，這不符合實際情況。當災情發生后，各受災點的受災情況相對確定，因此，公平性指標或權重變化都較小，不太可能出現較大波動。3) 研究中假設各應急物資配送中心車輛充足，但在實際救援中有可能出現車輛不足或車輛閑置等情況，因此，當出現車輛不足時需要進行調撥。為此，針對上述問題，本文作者提出物資配送中車輛分配公平性和配送及時性的協調優化模型，并采用基于啟發式算法、局部搜索算法和遺傳算法的混合智能算法進行求解，解決多配送中心、多受災點、多品種物資的車輛分配和物資配送問題。

1 問題描述與變量定義

1.1 問題描述與基本假設

研究的問題可描述為：在不斷變化救災環境中，在有限的時間和車輛資源條件下，通過科學合理的車輛分配方案，將有限的多品種物資在較短時間內從不同配送中心配送至各個受災點，同時實現車輛分配公平性的最大化。圖1所示為配送系統示意圖。

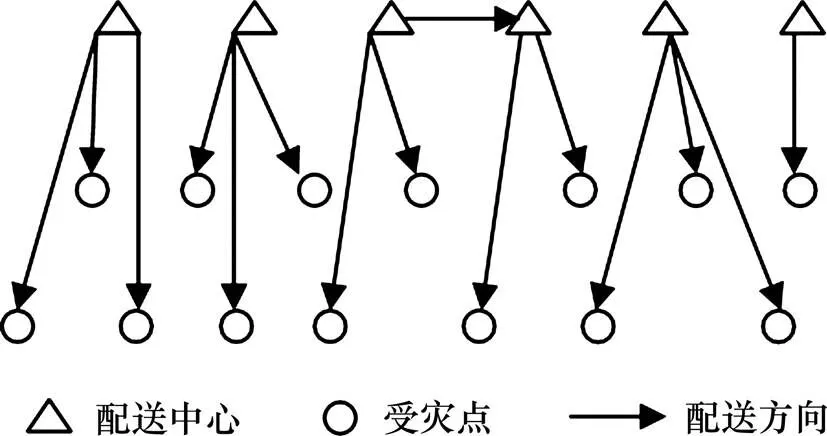
圖1 應急物流配送系統示意圖

本文中定義模型的假設條件如下：

1) 配送中心車輛充足，且車型相同；

2) 每輛車只執行1次配送任務，即從某配送中心出發，到達受災點完成配送任務；

3) 當其中1個配送中心車輛數不足時，可以從其他配送中心閑置車輛中調撥；

4) 配送中心與配送中心、配送中心與受災點的距離已知，且車輛的行駛速度不變；

5) 問題考慮的時間為運輸時間，物資裝卸載時間不予以考慮。

1.2 變量定義

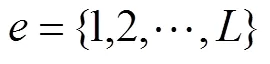
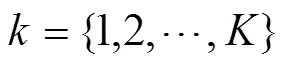
4) 目標函數：1為受災地區的總相對剝奪感，作為公平性目標；2為受災地區的總配送時間，作為及時性目標。

2 模型構建

2.1 車輛分配的公平性模型

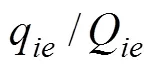
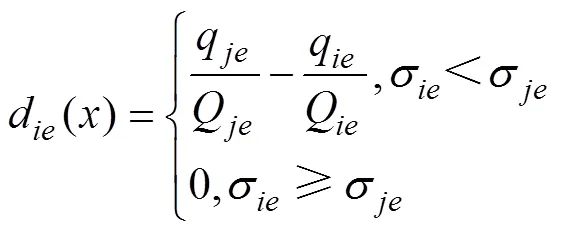
對于所有物資，受災點產生的總剝奪感為

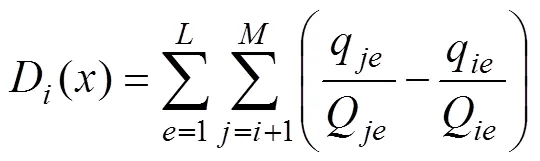
整個受災地區的總剝奪感為

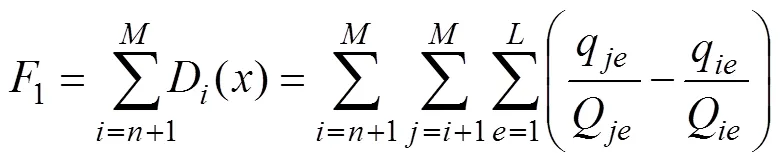
當1越小時，車輛分配的總剝奪感越小，感知的公平程度越高；反之，則公平程度越低。

2.2 物資配送的及時性模型

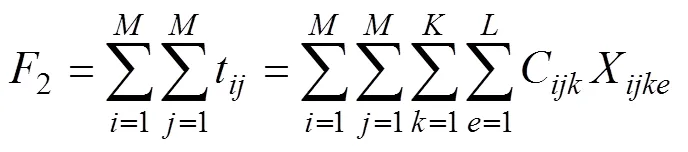
當2越小時，物資配送的時間越短，及時程度越高；反之，則及時程度越低。

2.3 車輛分配的公平性與物資配送及時性協調優化模型

在考慮多物資種類、多配送中心、多受災點等情況下，構建應急物資配送的多目標優化模型。該模型以車輛分配的公平性最大(相對剝奪感最小)和物資配送的及時性最好(配送時間最小)為目標，即

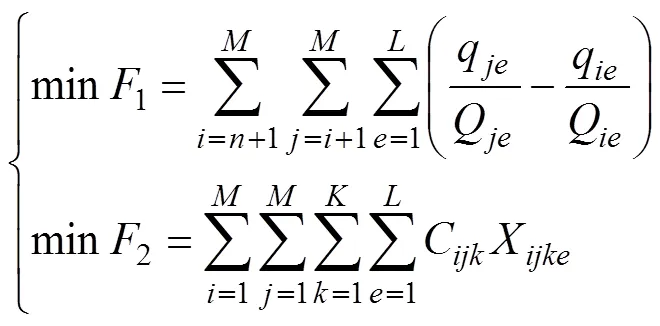
s.t.

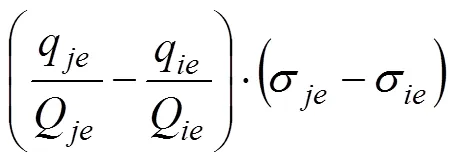
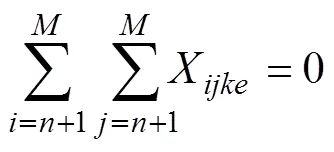
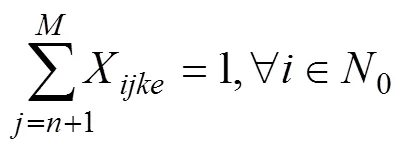
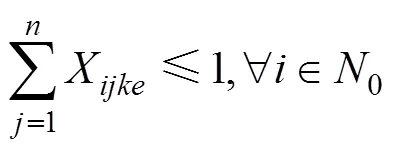
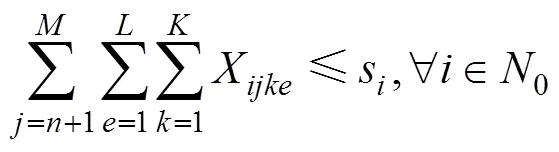
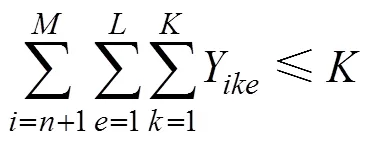
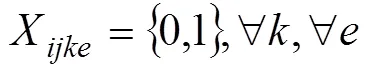
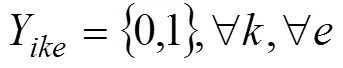
式(5)為公平性與及時性協調優化模型，其中1為車輛分配公平性目標函數，2為物資配送及時性目標函數。式(6)中左邊第1部分為受災點和受災點的配送物資的車輛數滿足率之差，第2部分為受災點和受災點的物資系數之差，不等式大于等于0，故這2部分必須同時大于等于0或者小于等于0，意味著物資系數越大的受災點，車輛滿足率應當越大；式(7)表示受災點之間不存在車輛配送；式(8)表示1輛車只能對1個受災點進行配送服務且僅服務1次；式(9)表示1輛車只能對1個配送中心進行車輛調撥服務且僅服務1次；式(10)~(11)為車輛數約束；式(12)~(13)為0?1約束。

3 模型求解

本文研究的協調優化問題是1個多目標整數規劃問題(MILP)，屬于NP-hard問題，不僅包括多受災區多品種物資的配送，而且包括配送中心的選擇，同時還要考慮配送中心擁有的車輛數限制、物資系數限制等約束條件。因此，該問題模型變量及約束條件眾多，求解困難。為解決此問題，采用基于啟發式算法、2?Opt局部搜索算法和遺傳算法的混合智能算法[14?20]進行求解。

3.1 歸一化處理

對于多目標優化問題，通常要轉化為單目標進行求解，方法有優選法、線性加權法、平方加權法、乘除法和分層序列法等。本文采用加權法，首先對多目標協調優化模型進行歸一化處理。

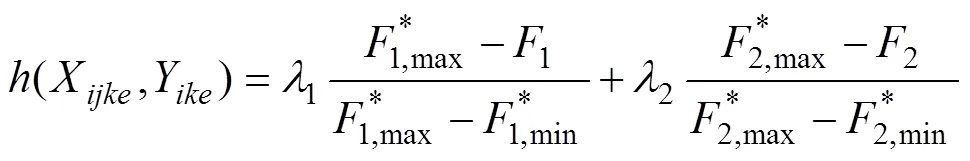
3.2 混合智能算法

將遺傳算法和啟發式算法、2?Opt局部搜索算法結合起來，構造求解應急車輛配送的公平性與及時性協調優化問題的混合智能算法(hybrid intelligent algorithm，HIA)。HIA的基本思想為：根據啟發式算法對種群結構進行調整，使種群中所有染色體合法化；采用2?Opt局部搜索算法來修正染色體中的車輛數，使車輛滿意率排序與其對應的物資系數排序一致；通過遺傳算法求解最優染色體和最優解，輸出最優車輛配送情況。

3.2.1 編碼

種群中每一條染色體包含若干個子串，每個子串表示對應配送中心的車輛配送情況，采用自然數編碼。配送中心編號用1，…，表示，受災點編號用+1，…，表示，物資編號用1，…，表示。圖2所示為染色體編碼結構。

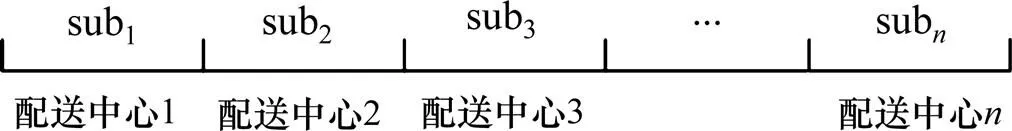
圖2 染色體結構

以子串sub為例。子串包含個基因段，=1, 2, …,。基因段1為始發配送中心編號，長度為1。其他基因段為每個受災點所需配送物資的車輛數，長度均為D，基因位=1, 2, …,D。圖3所示為具體 編碼。

例如有3個配送中心、3個受災點、3種物資，表1所示為車輛配送情況。本例中3個配送中心編號為1號、2號和3號，3個災點的編號為4號、5號和6號。染色體由3個子串組成，這些子串定義為sub1，sub2和sub3。sub1為1242000704，sub2為2000533403，sub3為3065309075。

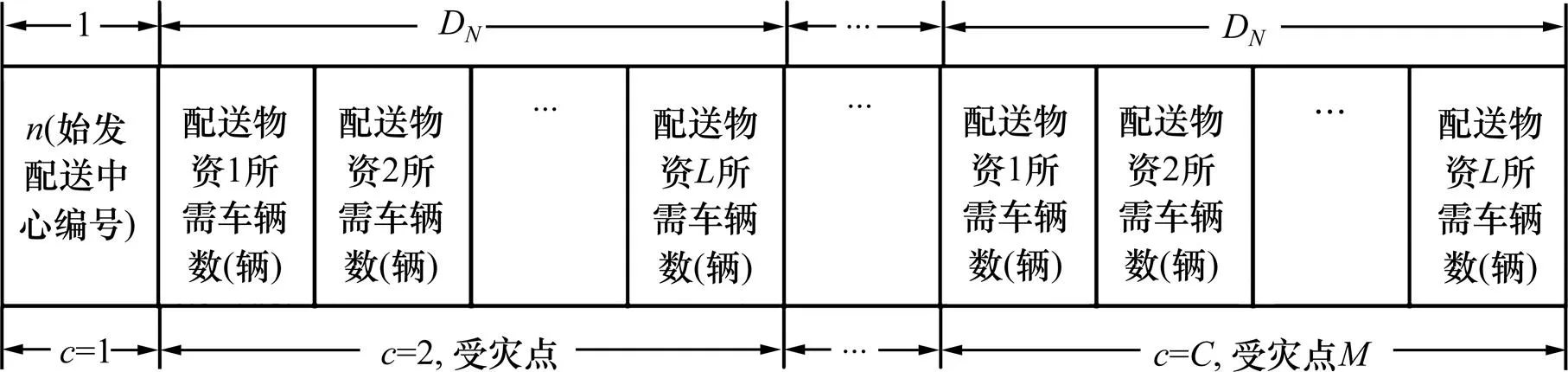
圖3 子串subn編碼示意圖

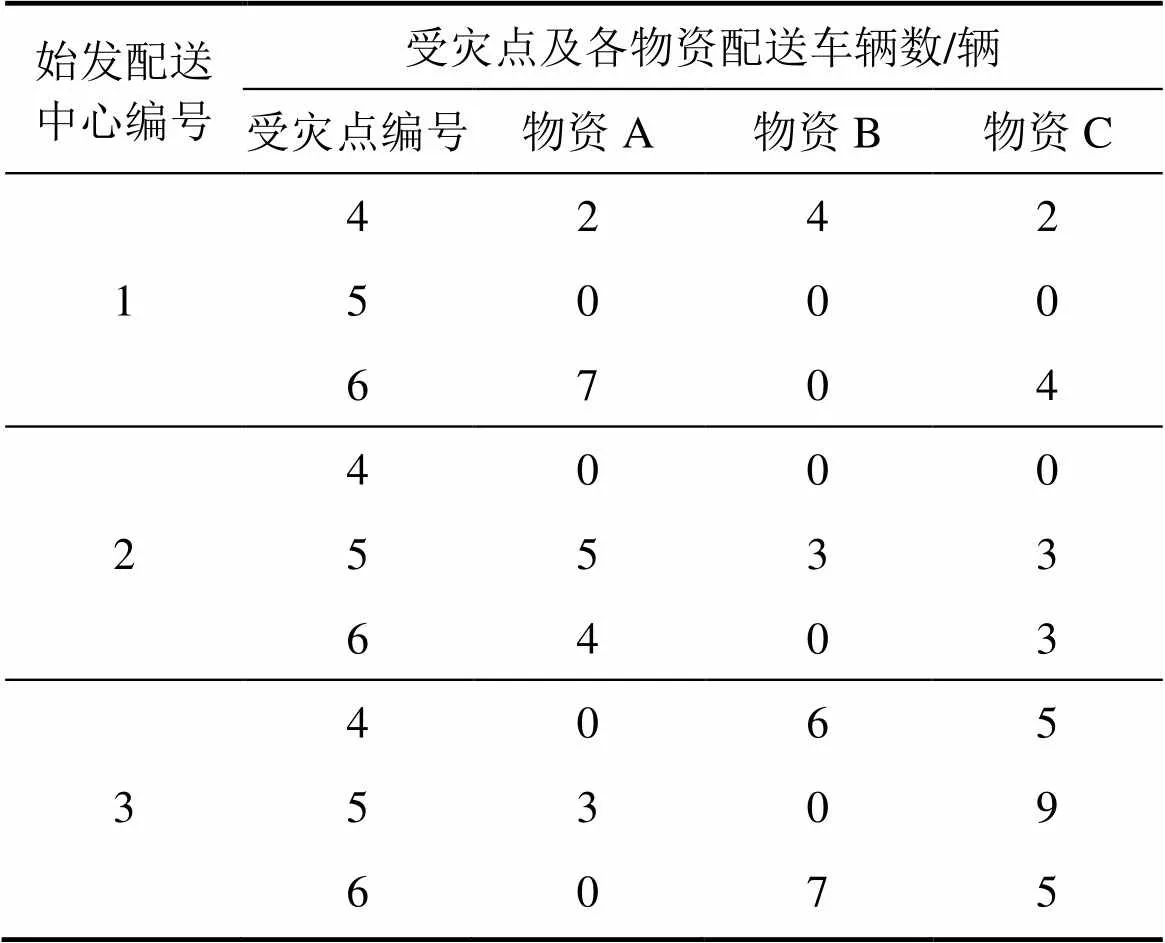
表1 車輛分配表

3.2.2 種群初始化及種群結構調整

根據染色體編碼規則隨機生成規模為popsize的初始種群。

由于隨機產生的染色體可能會發生配送車輛數超過配送中心車輛數，或者車輛滿意率不符合物資系數排序的情況，從而產生非法解。為了減少或者避免這些情況的發生，就需要對種群結構進行調整。首先要對每條染色體的車輛數進行評估，然后通過啟發式算法進行調整。具體的過程如下。

Step 1 計算每條染色體中的配送車輛數，并記錄。

Step 2對于配送車輛數超過配送中心車輛數的染色體，從中找出若干物資系數較小的受災點，將其車輛數清零，使該染色體合法化。同時將配送中心及這些受災點放入待選列表中。

Step 3根據啟發式算法中的最鄰近法和節約法，在保證配送車輛數可行的前提下，將待選列表的配送中心及受災點更新到已有染色體中。

Step 4 判斷待選列表是否所有配送中心和受災點都遍歷到，若列表中還有未遍歷的，則繼續進行Step 3，否則，則轉向Step 5。

Step 5 根據物資系數的排序，采用2?Opt局部搜索算法修正受災點的配送車輛數。

3.2.3 適應度計算

為評價模型種群中個體優劣，對每個染色體的適應度進行計算，從而獲得更優的染色體。將式(14)作為適應度函數，適應度最大的染色體為最優染色體。確定適應度函數為

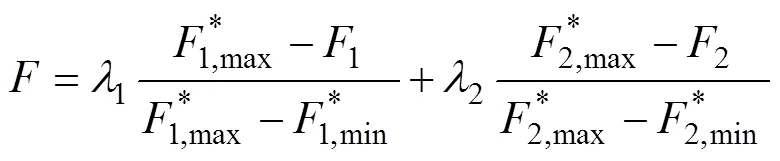
3.2.4 遺傳操作

1) 選擇操作。本文采用輪盤賭選擇策略，這樣既能保證目標函數值隨代數變得越來越小，又能使較好的個體以更大的概率保存。

2) 交叉操作。為了不破壞優良的子串，本文提出一種新的交叉算子，圖4所示為交叉操作示意圖。首先，隨機選擇2個父個體A和B，將其中一個父個體中物資系數最大的1條子串移到另一個父個體的臨時串首位；然后，刪除該父個體中與臨時串相同的基因；最后，將剩余的基因隨機全排列合并到臨時串中。

3) 變異操作。本文依據變異概率m，采用位移變異算子進行變異操作。方法是隨機選擇父個體A中2個非0編碼，交換其位置，從而產生新個體B。圖5所示為變異操作示意圖。

3.2.5 算法流程

根據HIA算法設計的基本思想，設計算法的具體步驟如下。

1) 種群的初始化。設定種群規模、最大迭代次數、權重系數，對染色體進行初始化。

2) 種群結構的調整。

3) 計算適應度。根據式(15)計算每條染色體的適應度。

4) 對每條染色體進行選擇、交叉和變異操作，更新子代種群。

5) 若未達到最大迭代次數，則返回2)。

6) 輸出最優染色體和最優解。

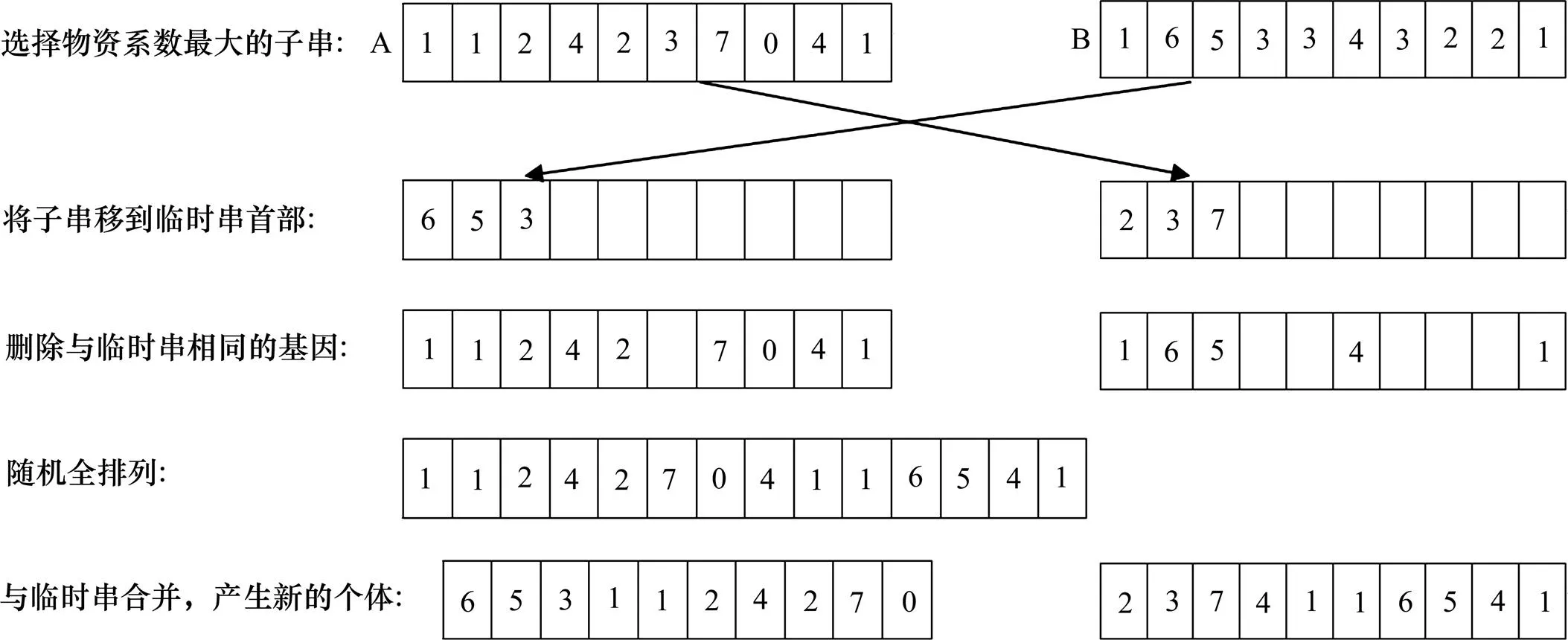
圖4 交叉操作示意圖

圖5 變異操作示意圖

4 仿真實驗分析

本文的算例分析分為3個部分：第1部分以Solomon測試數據庫中的算例數據，驗證本文提出的模型和算法的有效性；第2部分通過3個不同的實驗，將實驗結果與原算例中的結果進行分析對比，進一步驗證本文提出模型和算法的有效性；第3部分對雅安地震中應急物資配送進行仿真，驗證本文提出的模型和算法在實際應用中的效果。本文所有算例采用Matlab R2014a編程，在AMD四核A8-4500 M 1.90 GHz APU、內存為4 G的微機上進行求解。

4.1 算例仿真

為了驗證本文提出的模型和方法的有效性，將以Solomon測試數據庫中的RC201算例數據為基礎，并補充物資系數等相關數據，產生測試算例。具體方法如下：從RC201數據中隨機抽取13個坐標數據，其中3個作為配送中心，10個作為受災點，各點之間的距離采用直線距離表示，然后，隨機產生10個受災點的物資系數及車輛需求數。選擇的3個配送中心坐標為(2，45)，(8，56)和(45，65)，并分別命名為1號、2號和3號。假設每個配送中心初始配有30輛車。表2所示為各受災點物資系數及車輛需求數。

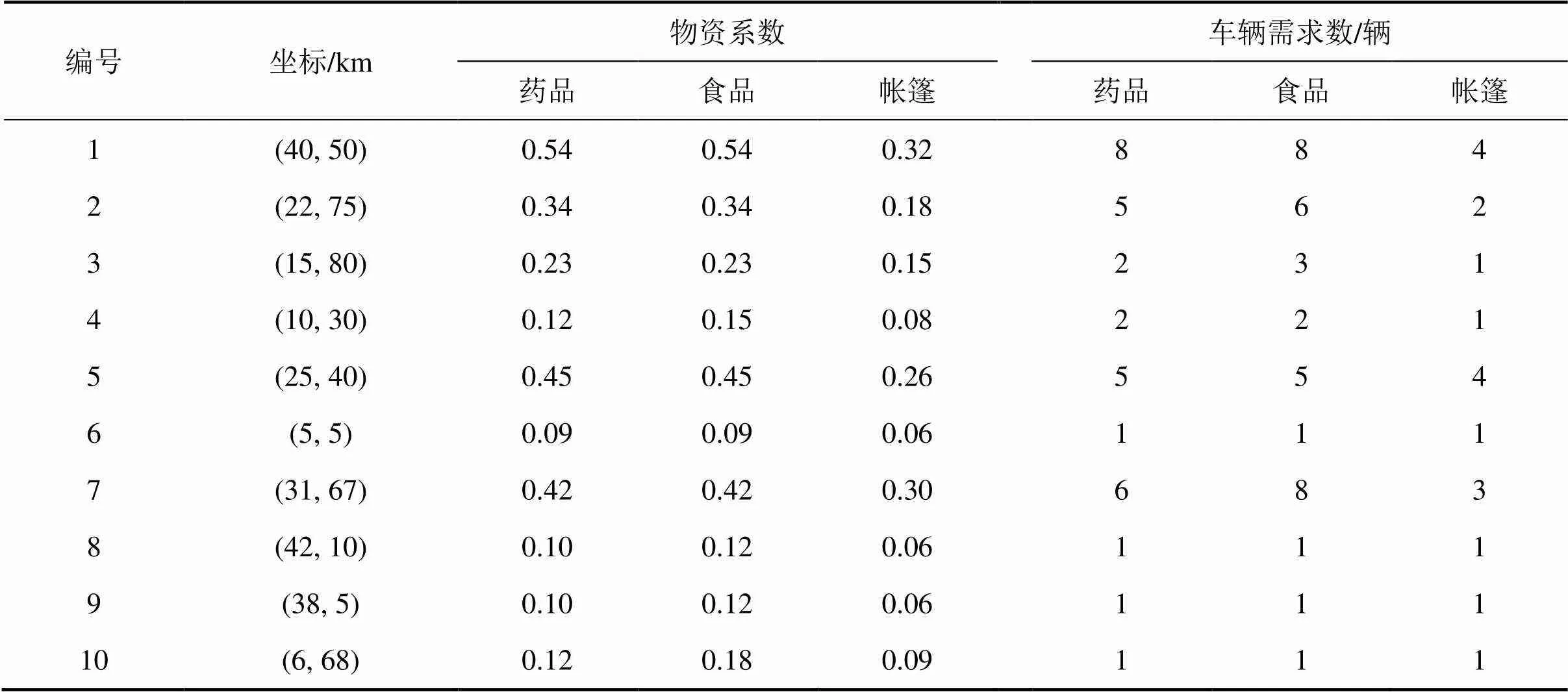
表2 原算例中各受災點初始數據

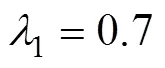
注：括號中數據為本著中心至受災點的車輛數

4.2 對比分析實驗

為了進一步驗證本文模型和算法的有效性，對如下3個問題進行比較分析：1) 配送中心車輛數不足時的物資配送問題；2) 目標函數的權重系數對HIA算法性能的影響；3) HIA算法和PSO算法求解結果的分析對比。

4.2.1 配送中心車輛數不足時的物資配送實驗

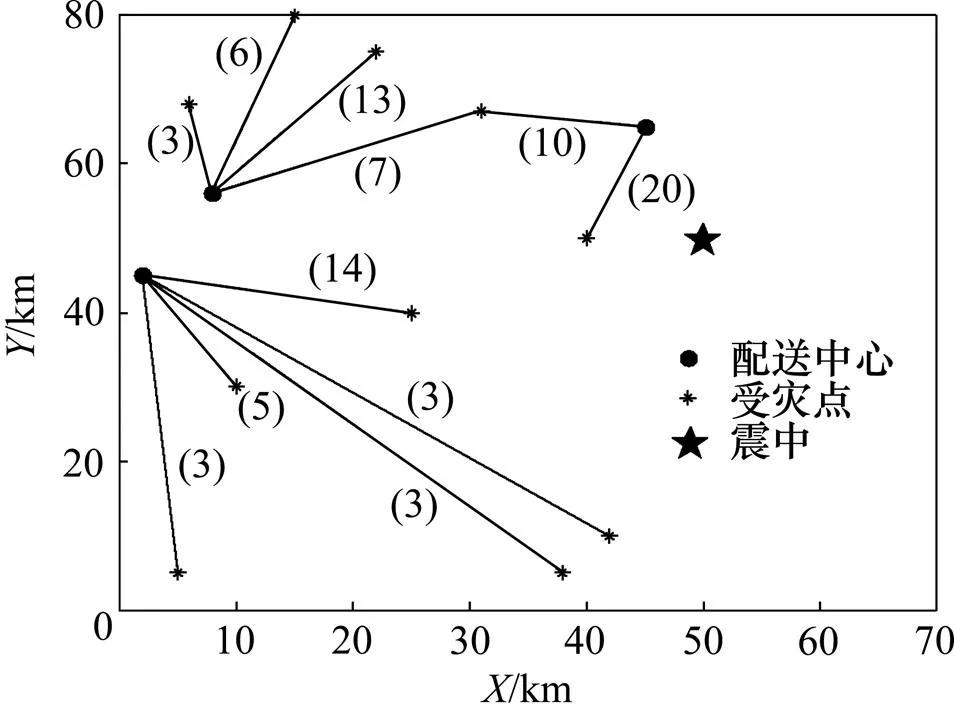
將原算例中1號、2號和3號配送中心的車輛數均減少為25輛，其他條件不變。圖7所示為車輛數不足時的配送示意圖。由于可配送車輛的總數為75輛，而受災點對于車輛的總需求數為87輛，因此，離震中較遠的、物資系數較小的受災點6、受災點8和受災點9不會分配車輛。而受災點1和受災點7由于離震中較近，物資系數較大，所需的配送車輛也較多，需要2個配送中心同時進行配送，以滿足它們的車輛需求。實驗可得到平均總配送距離為1 660.25 km，平均總配送時間為23.72 h。與原算例進行比較可以發現：當配送中心車輛數充足時，配送距離和配送時間的變化不會引起總剝奪感的變化；當配送中心車輛數不足時，物資配送距離和配送時間會減小，但總剝奪感會大幅度上升。

為了進一步探討當配送中心車輛數不足時公平性與及時性的關聯關系，本實驗通過5種不同車輛分配方案分析總剝奪感與總配送時間，結果如圖8所示。從圖8可以看出：當配送中心車輛數不足時，總配送時間和總剝奪感不能同時實現最小，提高公平性的同時會引起及時性降低，反之亦然。

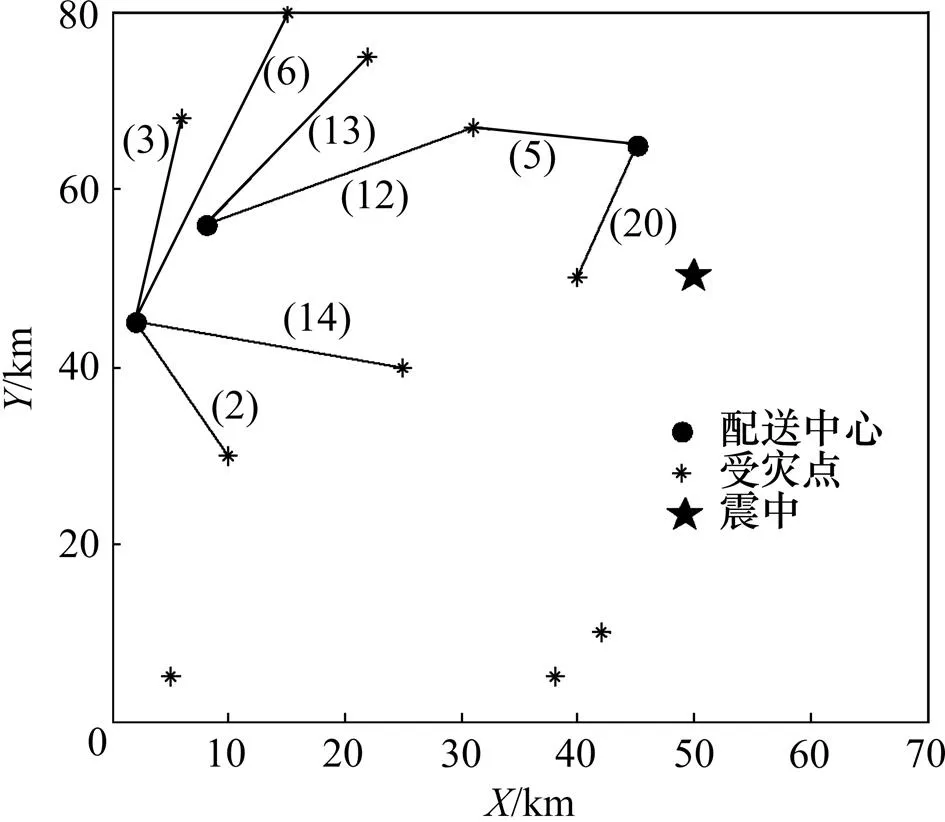
注：括號中數據為本著中心至受災點的車輛數

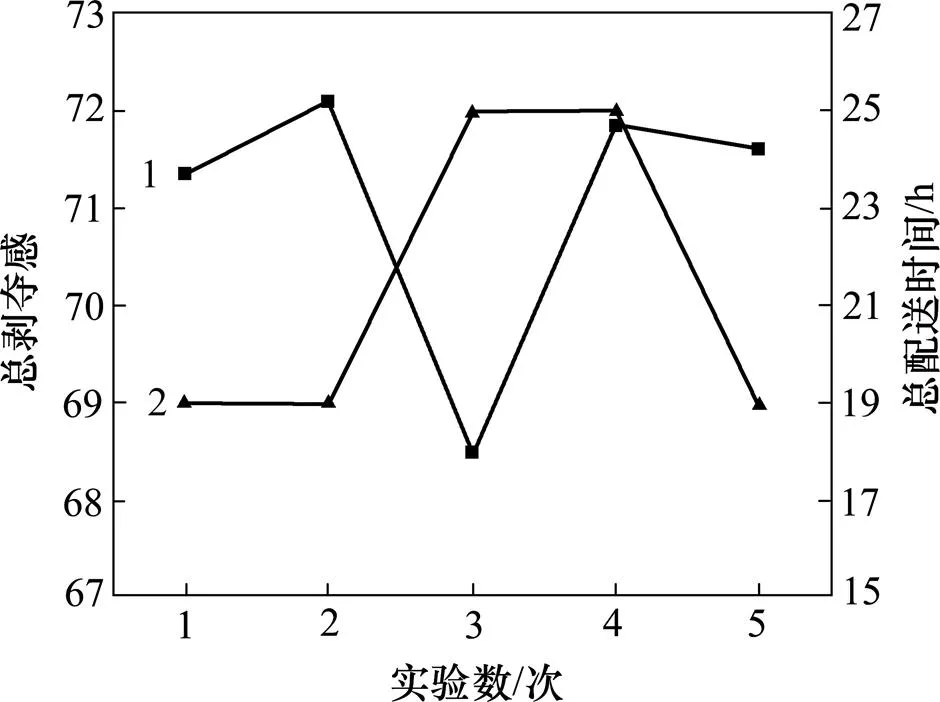
1—總配送時間；2—總剝壓感。

4.2.2 目標函數權重系數對HIA算法性能的影響

4.2.3 算法比較

為了更好地檢驗本文提出的HIA算法的性能，將該算法與微粒群PSO算法進行對比分析，分別對原算例進行10次求解，表3所示為計算時間數值實驗計算結果。從表3可知：隨著最大迭代次數增大，程序運行時間會有所增加，但HIA的計算時間總體上稍低于PSO的計算時間，其平均時間比PSO算法最大減少3.07%。基于模型最優解，在相同迭代次數下，HIA算法與PSO算法相比最大減幅達2.48%，減幅明顯，最優解也更優。

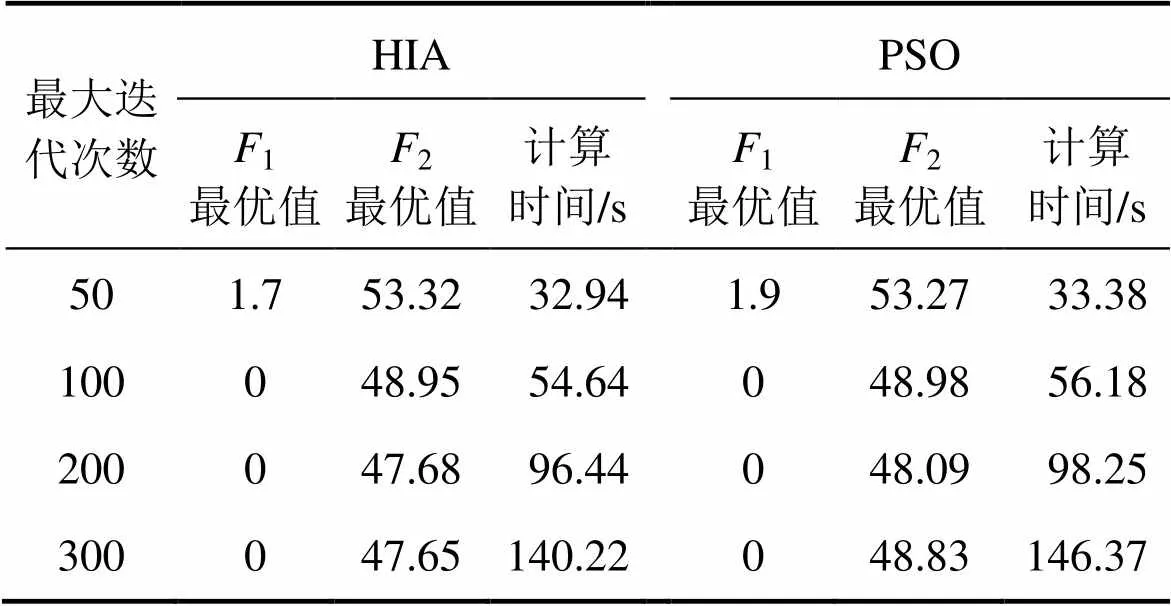
表3 不同算法計算時間比較

4.3 大規模算例分析

為了驗證本文提出的模型和算法在實際應用的效果，以2013?04四川雅安地區的7.0級強震為例進行分析。在這次地震中，雅安市區、龍門鄉、寶盛鄉、太平鎮、寶興縣、天全縣、名山區、滎經縣、漢源縣和石棉縣等地都不同程度受到影響，其中雅安市區、龍門鄉、天全縣等地受災嚴重，急需藥品、食品、帳篷等物資。已知雅安市區及周邊有3個應急配送中心，車型均為中型載貨汽車，每個配送中心均擁有100輛車，總數為300輛。表4所示為各受災點的物資系數及需求量，部分數據來源于文獻[6]。表5所示為車輛分配結果，圖10所示為配送示意圖。

由表5可知：在車輛充足的情況下，所有受災點的車輛需求都能得到滿足，滿足率達到100%，總剝奪感為0，實現了車輛分配的最大公平性。同時，計算得到總配送距離為6 628.8 km，總配送時間為94.7 h，表明在較短的時間內完成了大規模的應急物資配送任務。

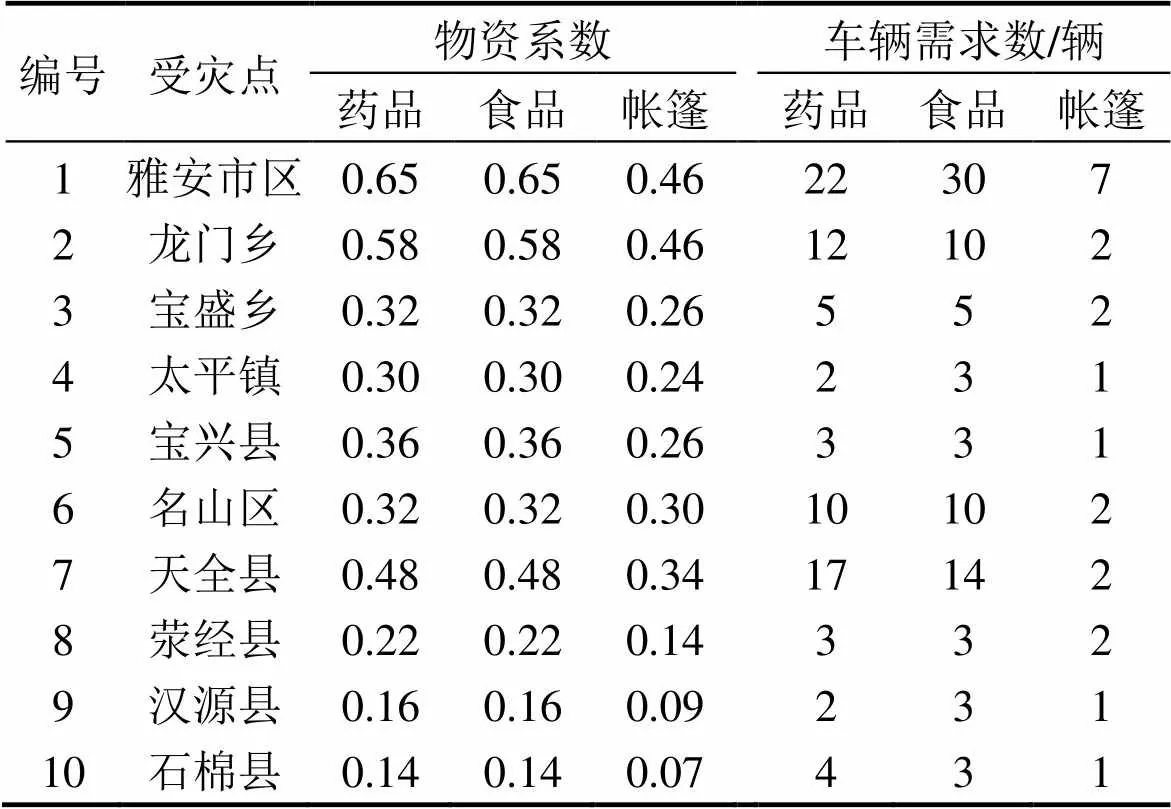
表4 大規模算例中各受災點初始數據

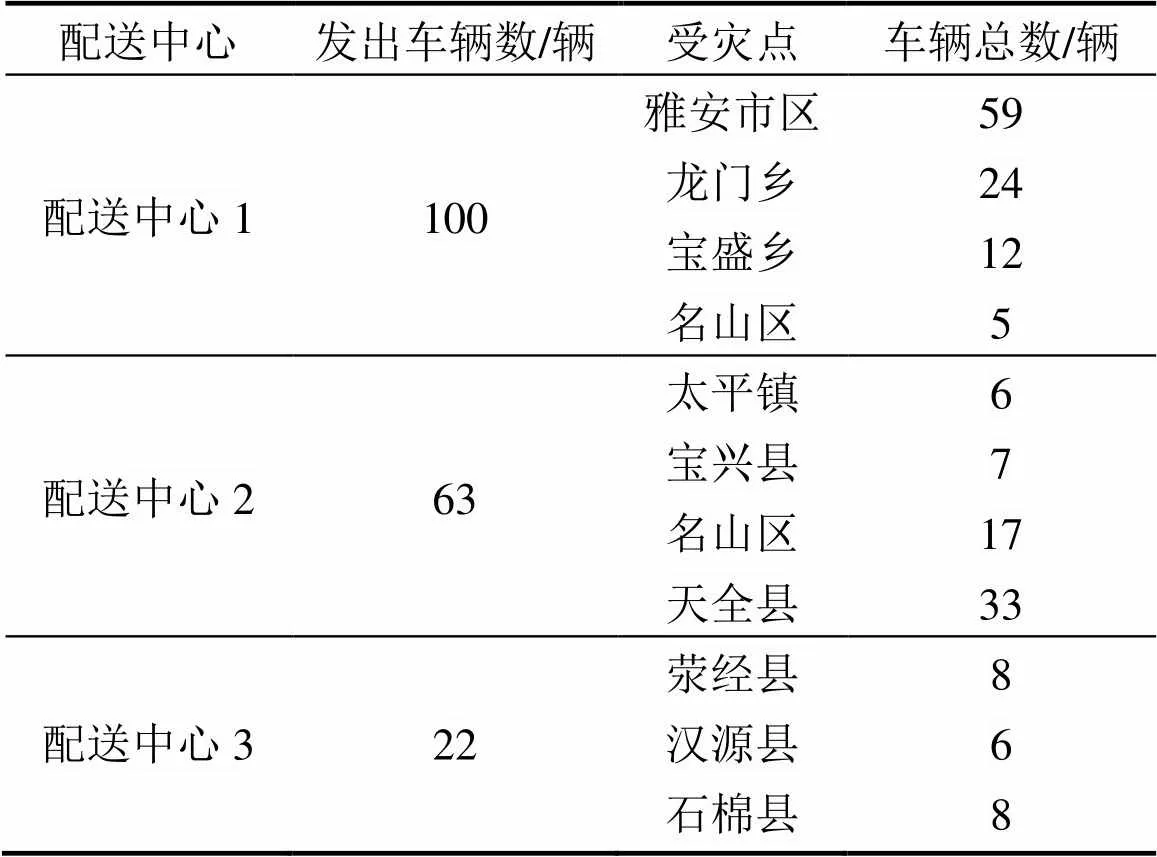
表5 車輛分配結果

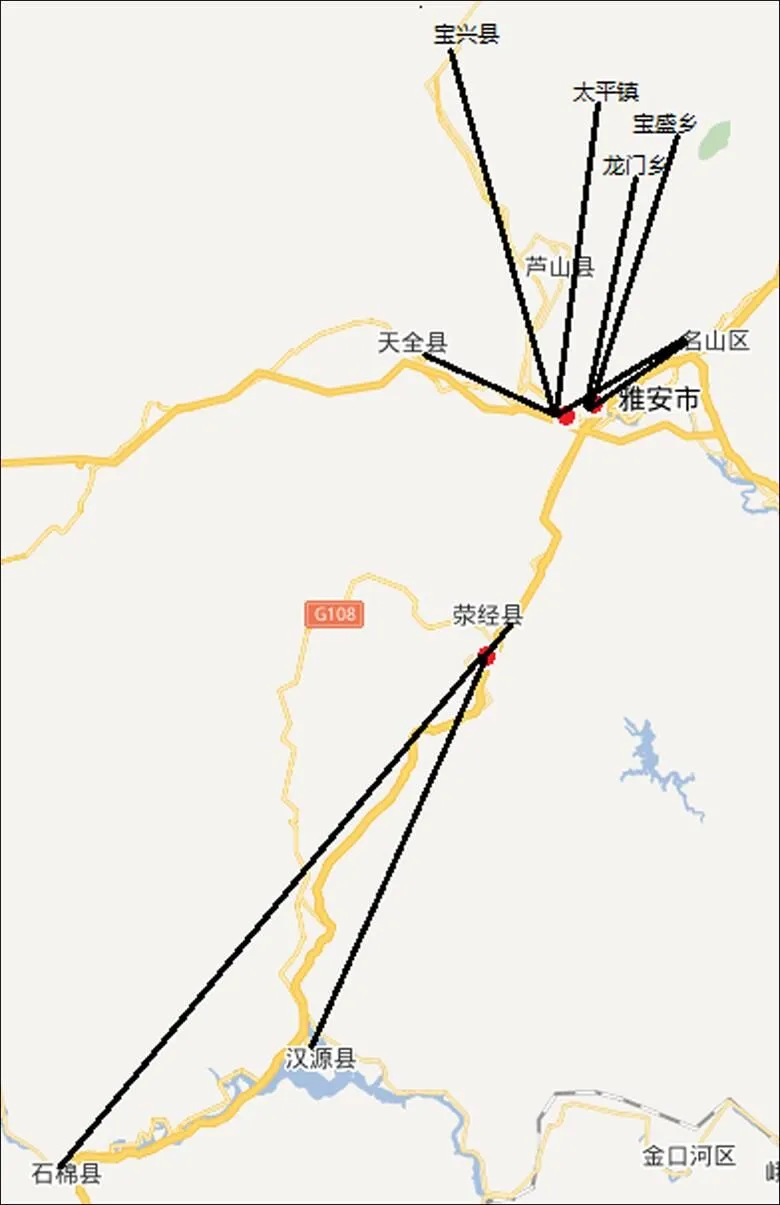
圖10 配送示意圖

5 結論

1) 針對應急救援中物資配送車輛分配的公平性與及時性問題進行分析，構建了協調優化模型，設計了一種基于啟發式算法、2?Opt算法和遺傳算法的混合智能算法對模型進行求解。

2) 設計了標準算例庫和四川雅安地震2個算例，共進行了5次數值實驗，都取得了比較理想的結果。該混合智能算法能快速有效地找到滿意解；當配送中心車輛數不足時，公平性與及時性存在關聯；目標權重對算法的穩定性和快速性有一定影響；該模型和算法在大規模地震實例中有效實現了公平性與及時性的協調優化。

3) 本文構建的模型主要有以下適用條件：在震后應急救援初期，配送中心車輛有限情況下藥品、食品和帳篷3種應急物資的配送，且需求已知；不適合于物資需求不確定的情況，因此，對需求不確定情況下的車輛分配問題有待進一步研究。

[1] 馬衛峰, 楊賽霓, 潘耀忠. 面向救災物資需求特征的自然災害應急響應[J]. 中國安全科學學報, 2010, 20(10): 171?176. MA Weifeng, YANG Saini, PAN Yaozhong. Relief demand characteristic-oriented emergency response in natural disasters[J]. China Safety Science Journal, 2010, 20(10): 171?176.

[2] CHANTA S, MAYORGA M E, MCLAY L A. The minimum p-envy location problem: a new model for equitable distribution of emergency resources[J]. Lie Transactions on Healthcare Systems Engineering, 2011, 1(2): 101?115.

[3] 馮春, 向陽, 薛坤, 等. 多周期多品種應急物資配送多目標優化模型[J]. 中國管理科學, 2017, 25(4): 124?132. FENG Chun, XIANG Yang, XUE Kun, et al. Multi-objective optimization model of the emergency logistics distribution with multi-cycle and multi-item[J]. Chinese Journal of Management Science, 2017, 25(4): 124?132.

[4] 張錦, 曾倩, 陳義友. 基于變權的物流資源公平分配方法[J]. 西南交通大學學報, 2017, 51(3): 563?570. ZHANG Jing, ZENG Qian, CHEN Yiyou. Equity allocation method of logistic resources based on variable weights[J]. Journal of Southwest Jiaotong University, 2017, 51(3): 563?570.

[5] BEHESHTI A K, HEJAZI S R, ALINAGHIAN M. The vehicle routing problem with multiple prioritized time windows: a case study[J]. Computers & Industrial Engineering, 2015, 90: 402?413.

[6] 胡志華, 董盼, 李清. 基于相對剝奪理論的救災物資運輸車輛分配公平性[J]. 上海海事大學學報, 2015, 36(2): 36?42. HU Zhihua, DONG Pan, LI Qing. Fairness of vehicle allocation for disaster relief materials based on relative deprivation theory[J]. Journal of Shanghai Maritime University, 2015, 36(2): 36?42.

[7] 王海軍, 杜麗敬, 馬士華. 震后應急物流系統中雙目標開放式選址：路徑問題模型與算法研究[J]. 管理工程學報, 2016, 30(2): 108?115. WANG Haijun, DU Lijing, MA Shihua. Model and algorithms for integrated open location and routing problem in emergency logistics under earthquake[J]. Journal of Industrial Engineering and Engineering Management, 2016, 30(2): 108?115.

[8] 劉長石, 彭怡, 寇綱. 震后應急物資配送的模糊定位?路徑問題研究[J]. 中國管理科學, 2016, 24(5): 111?118. LIU Changshi, PENG Yi, KOU Gang. Research on fuzzy location-routing problem in post earthquake delivery of relief materials[J]. Chinese Journal of Management Science, 2016, 24(5): 111?118.

[9] ZHOU Yawen, LIU Jing, ZHANG Yutong, et al. A multi-objective evolutionary algorithm for multi-period dynamic emergency resource scheduling problems[J]. Transportation Research Part E, 2017, 99: 77?95.

[10] OTHMAN S B, ZGAYA H, DOTOLI M, et al. An agent-based decision support system for resources' scheduling in emergency supply chains[J]. Control Engineering Practice, 2017, 59: 27?43.

[11] 鄭斌, 馬祖軍, 李雙琳. 基于雙層規劃的震后初期應急物流系統優化[J]. 系統工程學報, 2014, 29(1): 113?125. ZHENG Bing, MA Zujun, LI Shuangling. Integrated optimization of emergency logistics systems for post-earthquake initial stage based on bi-level programming[J]. Journal of Systems Engineering, 2014, 29(1): 113?125.

[12] 鄭斌, 馬祖軍, 周愉峰. 震后應急物流動態選址聯運問題的雙層規劃模型[J]. 系統管理學報, 2017, 26(2): 326?337. ZHENG Bing, MA Zujun, ZHOU Yufeng. Bi-level model for dynamic location transportation problem for post-earthquake relief distribution[J]. Journal of Systems & Management, 2017, 26(2): 326?337.

[13] 陳瑩珍, 趙秋紅. 基于公平原則的應急物資分配模型與算法[J]. 系統工程理論與實踐, 2016, 51(3): 563?570. CHEN Yingzhen, ZHAO Qiuhong. The model and algorithm for emergency supplies distribution based on fairness[J]. Systems Engineering Theory & Practice, 2016, 51(3): 563?570.

[14] GIANFRANCO F, SIMONA M, CLAUDIA P, et al. An emergency vehicles allocation model for major industrial disasters[J]. Transportation Research Procedia, 2017, 25: 1164?1179.

[15] AHMAD M, SAEED Y A. Bi-objective stochastic model for emergency medical services network design with backup services for disasters under disruptions: an earthquake case study[J]. International Journal of Disaster Risk Reduction, 2017, 23: 204?217.

[16] 胡飛虎, 田朝暉, 趙沐華, 等. 基于遺傳算法的應急物資分層聯動分配研究[J]. 計算機應用研究, 2016, 33(2): 440?443. HU Feihu, TIAN Zhaohui, ZHAO Muhua, et al. Research on hierarchical linkage scheduling emergency supplies based on genetic algorithm[J]. Application Research of Computers, 2016, 33(2): 440?443.

[17] 劉家利, 郭秀萍. 存在產品互斥和車輛匹配的多中心開環車輛路徑問題[J]. 系統管理學報, 2016, 25(1): 129?138. LIU Jiali, GUO Xiuping. Multi-depot open vehicle routing problem with exclusive products and heterogeneous vehicles[J]. Journal of Systems & Management, 2016, 25(1): 129?138.

[18] BARKAOUI M, BERGER J, BOUKHTOUTA A. Customer satisfaction in dynamic vehicle routing problem with time windows[J]. Applied Soft Computing, 2015, 35: 423?432.

[19] SASO K, VILI P. A survey of genetic algorithms for solving multi depot vehicle routing problem[J]. Applied Soft Computing, 2015, 27: 519?532.

[20] 許茂增, 余國印, 周翔, 等. 綜合成本最小的低碳車輛調度問題及算法[J]. 計算機集成制造系統, 2015, 21(7): 1906?1914. XU Maozeng, YU Guoying, ZHOU Xiang, et al. Low-carbon vehicle scheduling problem and algorithm with minimum- comprehensive-cost[J]. Computer Integrated Manufacturing Systems, 2015, 21(7): 1906?1914.

(編輯 陳燦華)

Integrated decision making of emergency vehicle allocation and emergency material distribution

WANG Li1, ZHOU Xiancheng2, ZHAO Zhixue1, LIU Limei1, YU Lingli3

(1. School of Computer and Information Engineering, Hunan University of Commerce, Changsha 410025, China; 2. Hunan Collaborative Innovation Center of Mobile E-commerce, Hunan University of Commerce, Changsha 410025, China; 3. School of Information Science and Engineering, Central South University, Changsha 410083, China)

In the delivery of relief aids to the disaster areas, it is usually difficult to balance the fairness of vehicle allocation and the timeliness of materials distribution. To solve the problem, a multi-objective coordination optimization model was presented. The objective was to minimize the relative deprivation of the vehicle allocation(fairness) and the delivery time(timeliness). To solve the model, a hybrid intelligent algorithm combining a heuristic algorithm, a local search algorithm and a genetic algorithm was designed. The results show that there is a close relationship between fairness and timeliness when the number of vehicles in distribution centers is insufficient. The proposed algorithm is fast and effective to find the satisfactory solutions. The target weight coefficients have influence on the stability and rapidity of the algorithm. The model and algorithm are also effective in large-scale earthquake instances.

emergency materials distribution; relative deprivation; fairness; timeliness; coordinative optimization

10.11817/j.issn.1672-7207.2018.11.018

TP 391.9

A

1672?7207(2018)11?2766?10

2017?12?26；

2018?03?06

國家自然科學基金資助項目(61403426)；商務智能湖南省重點實驗室資助項目(2015TP1002)；教育部人文社科基金資助項目(14YJCZH099)；湖南省自然科學基金資助項目(2018JJ3261)；湖南省教育廳科研項目(15C770) (Project(61403426) supported by the National Natural Science Foundation of China; Project(2015TP1002) supported by Key Laboratory for Business Intelligence of Hunan Province; Project (14YJCZH099) supported by the Humanities and Social Sciences Planning Fund of Ministry of Education; Project(2018JJ3261) supported by the Natural Science Foundation of Hunan Province; Project(15C770) supported by the Scientific Research Fund of Department of Education of Hunan Province)

周鮮成，博士，教授，從事物流系統的建模與優化以及管理信息處理研究；E-mail: zxc6501@126.com