淺析標(biāo)準(zhǔn)差及其在工程統(tǒng)計(jì)中的運(yùn)用
黃春富
江蘇龍川水利建設(shè)有限公司 江蘇 揚(yáng)州 225200
1 標(biāo)準(zhǔn)差的概念
標(biāo)準(zhǔn)差是指個(gè)體數(shù)據(jù)與均值離差平方和的算術(shù)平均數(shù)的算術(shù)根。總體標(biāo)準(zhǔn)差用σ表示;樣本標(biāo)準(zhǔn)差用s表示。其計(jì)算公式為:
1.1 總體標(biāo)準(zhǔn)差σ
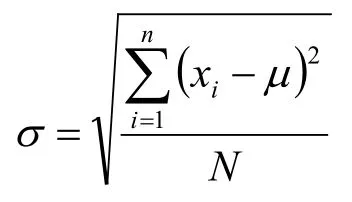
1.2 樣本標(biāo)準(zhǔn)差s
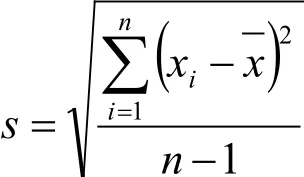
實(shí)際應(yīng)用中多為接觸的是樣本,所謂標(biāo)準(zhǔn)差一般也是指樣本標(biāo)準(zhǔn)差。當(dāng)樣本容量較大(n≥50)時(shí),上式中的分母( 1-n )可簡化n。
2 樣本標(biāo)準(zhǔn)差的多種表達(dá)式
公式(1)以前常見,現(xiàn)行《水利水電工程施工質(zhì)量檢驗(yàn)與評定規(guī)程》(SL176-2007[1])仍然采用;公式(2)在建設(shè)工程中現(xiàn)多用于統(tǒng)計(jì)法評定混凝土強(qiáng)度,如《混凝土強(qiáng)度檢驗(yàn)評定標(biāo)準(zhǔn)》(GB/T50107-2010[2])、《水閘施工規(guī)范》(SL27-2014[3])、江蘇省地方標(biāo)準(zhǔn)《水利工程施工質(zhì)量檢驗(yàn)與評定規(guī)范》(DB/T2334-2013)等;公式(3)見于某類計(jì)算器。
2.1 其他衍生表達(dá)式
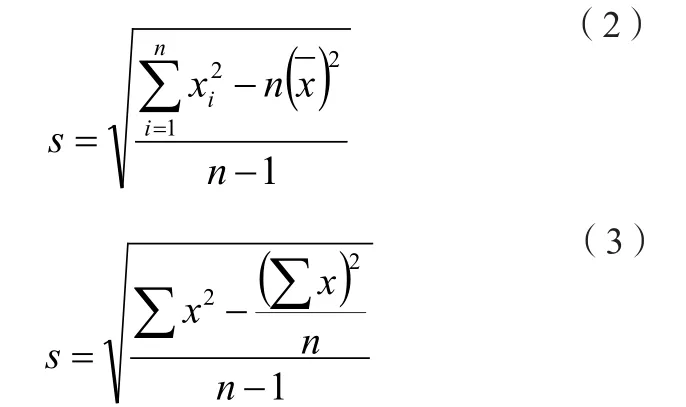
2.2 不同表達(dá)式的樣本標(biāo)準(zhǔn)差值相等
這便于我們無須糾結(jié)采用不同的公式是否得出不同的結(jié)果。要證明不同表達(dá)式的樣本標(biāo)準(zhǔn)差值相等,只需證明
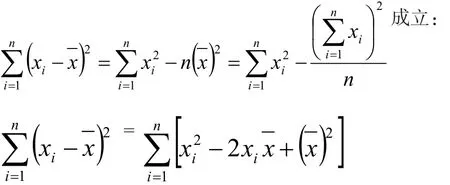
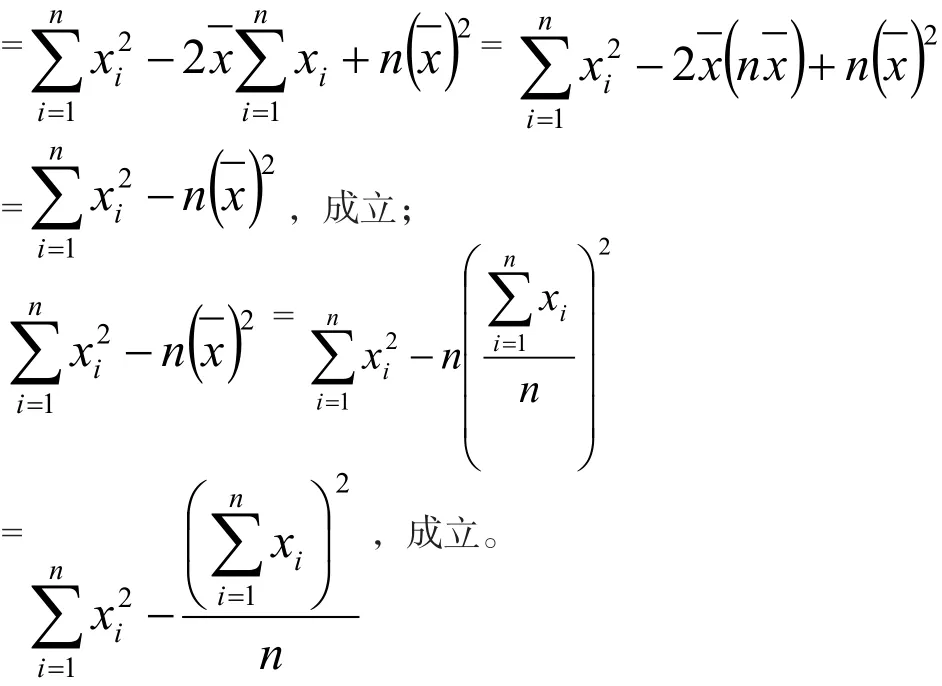
事實(shí)對于同樣的驗(yàn)收批,采用不同的公式計(jì)算,其結(jié)果是一致的。
3 樣本標(biāo)準(zhǔn)差在工程統(tǒng)計(jì)中的應(yīng)用注意事項(xiàng)
3.1 注意區(qū)分總體標(biāo)準(zhǔn)差和樣本標(biāo)準(zhǔn)差
現(xiàn)在的統(tǒng)計(jì)都實(shí)行電算化,電算界面很容易出現(xiàn)總體標(biāo)準(zhǔn)差和樣本標(biāo)準(zhǔn)差的選項(xiàng),容易混淆我們所需要的樣本標(biāo)準(zhǔn)差。如何區(qū)分?可以比較兩者的值,大者即為樣本標(biāo)準(zhǔn)差。
3.2 中間過程數(shù)據(jù)修約對最終計(jì)算結(jié)果的影響
水利工程施工質(zhì)量檢驗(yàn)與評定規(guī)范(DB32/T2334-2013[4])填寫要求與示范中有如下示例:
某一評定批的混凝土試塊強(qiáng)度等級為C25,共取樣17組,試驗(yàn)齡期均為28d,強(qiáng)度(MPa)分別為:27.6、29.4、31.2、29.8、35.8、36.2、34.2、32.7、39.7、31.4、35.7、28.8、35.3、32.6、31.8、29.9、33.6。

在進(jìn)行科學(xué)實(shí)驗(yàn)的數(shù)據(jù)記錄、數(shù)據(jù)處理和計(jì)算過程中,最重要的就是要保證實(shí)驗(yàn)數(shù)據(jù)的準(zhǔn)確性和可靠性。如果存在人為修約(除非規(guī)定這樣做)中間數(shù)據(jù),那將會影響最終計(jì)算結(jié)果的準(zhǔn)確性,進(jìn)而可能造成誤判[5]。
當(dāng)今計(jì)算器/計(jì)算機(jī)已很普遍,復(fù)雜的數(shù)據(jù)運(yùn)算可交由它們來處理,且定能得到足夠滿足準(zhǔn)確度要求的最終數(shù)據(jù)。因此,先計(jì)算最后修約,是計(jì)算機(jī)時(shí)代值得提倡的運(yùn)算順序。現(xiàn)在最簡單的函數(shù)計(jì)算器,都帶有基本的統(tǒng)計(jì)功能,總體標(biāo)準(zhǔn)差、樣本標(biāo)準(zhǔn)差、平方和、均值等參數(shù)一應(yīng)俱全,輸入樣本數(shù)據(jù)后即可準(zhǔn)確得到。

