基于GSFLOW的片麻巖地區地表水和地下水耦合作用分析

何 君

（山東省淮河流域水利管理局規劃設計院，山東 濟南 250000）

近些年來，水資源短缺已經成為全球面臨的一個重要的問題，水溫循環規律對于水資源的時間和空間分布具有重要的作用，隨著人類氣候的不斷變化，地下水的過度開采，水資源的異地調用，導致不同區域的地表水和地下水相互作用越來越明顯和頻繁。近些年來，過度的水資源開采、水資源污染和全球變暖等氣候變化對水資源和生態環境造成了極大的影響，地表水和地下水之間的相互作用也變的非常復雜，這種變化對于水資源的保護和合理利用產生了極大的影響。因此為了掌握人類活動和氣候變化對水流域水循環的影響規律和機理，因此需要從過程上對地表水和地下水耦合進行分析。本文通過GSFLOW軟件對地表水和地下水構建水文模型，對采集的水文數據進行地表-地下水流耦合模擬分析。

1 理論分析

1.1 地表水地下水相互作用概念模型

根據研究流域的水文條件、地址條件和地表水地下水循環特征建立地表水-地下水相互作用過程的概念模型，對水流的蒸發、徑流和地表水地下水相互作用吉林進行描述。同時及時考慮流域下墊面的影響，對于下墊面的改進對水循環的過程的影響進行分析，通過考慮下墊面可以更精確的對水循環的空間分布進行模擬，得到更加精確的計算結果。地表水地下水相互作用模型如圖1-A所示：

圖1 -A 地表水于地下水相互作用過程圖

1.2 GSFLOW計算原理

GSFLOW軟件主要包括三個計算模塊，第一個模塊主要進行能量水流和水量的計算，采用PRMS模型進行模擬。第二個模塊采用二次開發程序包對河流和湖泊進行模擬計算。第三個模塊是土壤層以下區域，利用UZF等程序包進行模擬計算。GSFLOW通過將流域劃分為透水區和不透水區進行水流計算，計模型如下式所示：

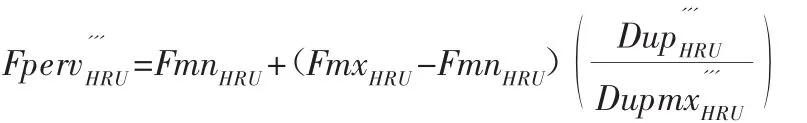
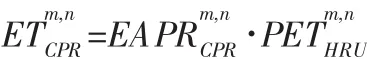
式中：celtop為有限差分單元格的頂板海拔；DSZ為土壤層底部重力排泄受地下水位影響的波動深度；CNDSZ為土壤區導水系數；

地下水位模擬計算公式如下所示：

式中：Kxx、Kyy、Kzz為滲透系數沿著 x、y、z軸方向的主要分量；h為水頭；W為地下水的源和匯，SS為多孔介質的貯水率，t為時間步長。

2 研究區域概況

研究流域位于山東省威海市，流域面積約為1391 km2，流域內最大河流長度為65 km，該流域地勢平坦，最高海拔約為896 m。該流域山區面積占總面積的17%左右。大部分丘陵山地還把在700 m左右，其中200 m～300 m的波狀丘陵分布最為廣泛，坡度為25度以下。土地利用/覆蓋主要為耕地，約占流域面積的68.2%，居民地12.96%，林地12.5%，草地 3.42%，水域2.66%，其余為裸地。流域地形圖見圖1-B。

圖1 -B 流域地形示意圖

該流域屬暖溫帶東亞季風區大陸性氣候，四季分明，春季風大干燥，多有春旱；夏季濕熱多雨，偶有伏旱；秋季溫和涼爽，時有連陰雨及秋旱；冬季漫長，盛行干冷冬季風。多年平均氣溫11.5℃，歷年極端最高氣溫36.4℃，極端最低氣溫-25.5℃。由于季風進退遲早和強弱的不同，降水的年度變化很大。年內分配不均，汛期降水量占年降水量的72%。多年平均年降雨量818 mm，最多處在昆崳山頂達1093 mm，流域內陸面蒸發為500 mm左右。研究區降雨分布見圖2。

圖2 該流域降雨分布圖

研究區為第四系沖洪積、沖海積、海積、湖沼積的砂、砂礫層，巖性多為細砂、中粗砂夾礫石，流域內地下水位較淺、含水層富水性較弱，地下水主要接受降水入滲補給和河水補給，多數沿地形向河谷匯集，局部受隔水層影響，在山腰或山頂出露形成山泉，但水量極小，單井出水量一般在5 m3/h～20 m3/h，極個別的單井出水量可達80 m3/h。地下水類型主要為基巖裂隙水和第四系孔隙水。基巖裂隙水主要賦存于變質巖、花崗巖和碎屑巖的風化裂隙和構造裂隙中，富水性較弱，一般埋藏較深，約為2 m～30 m，開發較為困難。基巖裂隙水的主要排泄途徑：一是匯集于河谷形成河川基流；二是側滲補給第四系或直接排泄入海；三是消耗于分散的人工開采。

圖3 該流域水文地質圖

3 數值模擬結果分析

(1)數值模型的建立

根據現有的地質和水文資料，對GSFLOW三維計算模型進行網格劃分。共劃分為110000個網格，共有76987個活動網格，為了計算方便將數值模型蓋化為兩層，其中第一層為含水層，第二層為承壓含水層。數值模型如圖4所示。采用模型計算初始時段的淺層地下水水位，通過水位計算方法，獲得含水層的初始水位，通過模擬計算，對上下兩層的初始滲流場進行模擬。含水層滲透系數的確定主要參考研究區滲透系數空間變異性分析成果，孔隙度及給水度、降雨入滲系數等水文地質參數主要根據水文地質資料確定。

圖4 數值計算模型

(2)GSFLOW模擬結果

圖5 某流域流量模擬結果與實測值對比圖

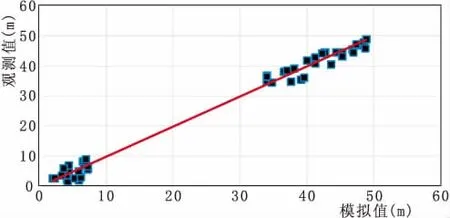
圖6 地下水位對比圖

將流域內的月徑流量模擬結果與檢測結果進行對比分析如圖5所示，從整體數據變化趨勢來看，數值模擬計算結果與檢測結果具有較好的對應性。在概率期，確定性系數為0，85，在模型期，確定性系為0.76，在這兩個時期模型的確定性系數均大于0.7，并且概率期確定性系數比模型期概率系數大11.8%，對于大流域流量模擬來說，采用GSFLOW模型模擬結果較好，精度較高。如圖6所示為，在模擬期間地下水位擬合結果圖，如圖所示擬合結果所示，檢測水位的計算值與觀測值的誤差為0.3 m，相關系數為0.925，符合模擬要求。

(3)地下水開采對地表水和地下水相互作用的分析

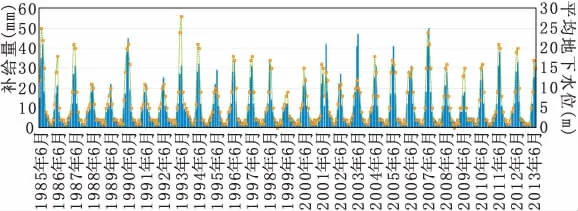
圖7 現狀開采下地下水位模擬結果

圖8 減少50%開采下地下水位模擬結果

圖9 不同開采方案向下地下水側向補給量與河道基流量模擬結果

通過圖7～8可知，隨著地下水開采的減少，地下水位動態特征呈現升高趨勢，在現狀地下水開采情況下，隨著地下水開采量的減少，河道基流量為由0逐漸變恢復河道基流量，同時地下水側向補給量也一定程度上增加，通過模擬分析可知，在地下水開采過程中，隨地下水位的增加河道基流量呈現增加趨勢。

4 結論

(1)通過對流域內水流進行模擬分析可知，在概率期，確定性系數為0.85，在模型期，確定性系為0.76，在這兩個時期模型的確定性系數均大于0.7，并且概率期確定性系數比模型期概率系數大11.8%，檢測水位的計算值與觀測值的誤差為0.3 m，相關系數為0.925，符合模擬要求。

(2)隨著地下水開采的減少，地下水位動態特征呈現升高趨勢，隨著地下水開采量的減少，河道基流量為由0逐漸變恢復河道基流量，同時地下水側向補給量也一定程度上增加在地下水開采過程中，隨地下水位的增加河道基流量呈現增加趨勢。