峽門河水文預報方案建立與修正

郝 強

（甘肅省武威水文水資源勘測局，甘肅 武威 733000）

水文預報是現代水文學科的分支，是建立在充分掌握客觀水文規律的基礎上，預報未來水文現象的一門應用科學技術[1]。目前，許多流域水文測驗設施的密度，無法滿足建立高精度的水文預報方案，而水文要素作為典型的時間序列要素，具備時間序列統計分析的可行性[2]，鑒于此，基于統計學方法的長期預報在小流域水文預報探索階段有無可比擬的優勢。

作為區域經濟支撐點哈溪鎮的過境河流，峽門河長期缺乏必要預報手段，不利于抗旱防洪，開展相關研究勢在必行。本文將以峽門河33年實測數據為支撐，探索符合實際、具備一定精度的長期預報方案，并嘗試對2018年水情進行預報。

1 流域概況

峽門河又稱黃花灘河，屬石羊河二級支流，發源于祁連山北麓甘肅天祝縣與青海門源縣交界處的青分嶺、紅腰峴以東，沿東偏北向至天祝縣哈溪鎮與哈溪河匯合成黃羊河，全長34 km，流域面積325 km2，多年平均降水量489 mm，多年平均徑流量0.847億m3。從1989年至2008年，總體上天然來水量為減少趨勢，年際變幅大。最小年徑流量0.5798億m3發生在2013年，最大年徑流量1.482億m3發生在1993年。徑流年內分配極不均衡，4月～10月徑流量占總量87%以上，11月至次年3月徑流量不到總量14%，一般最小徑流出現在2月份。

2 研究方法

2.1 周期均值迭加法

將水文要素的時間變化過程概化為多個周期序列的迭加，通過F檢驗判定有k個顯著周期，則其數學形式表示為：

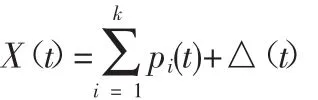
其中X（t）為t時刻水文要素，pi(t)為t時刻的第i周期，△（t）為 t時刻誤差[3]。

如果判定存在若干顯著周期，通過順序周期迭加就可以實現預報。

2.2 ARIMA模型法

ARIMA模型(Autoregressive Integrated Moving Average Model)，全稱為自回歸積分滑動平均模型，是指將預測對象的時間變化過程視為一個隨機序列，用一定的數學模型來近似描述，從而將非平穩時間序列轉化為平穩時間序列，然后將因變量僅對它的滯后值以及隨機誤差項的現值和滯后值進行回歸所建立的模型[4]、[5]。數學模型確定后就可以通過時間序列的實際值來預測未來值。

借助SPSS的時序分析模塊可以實現ARIMA模型預報。

3 預報演算

使用峽門臺水文站（1985年～2007年）與哈溪水文站（2008年～2017年）實測數據，進行周期均值迭加演算與ARIMA模型演算，確定參數值。

3.1 周期均值迭加演算

在數據文件yubaodata1.xls中新建工作表，復制實測數據，保存文件。

打開周期均值迭加程序，選擇預報站點為哈溪，預報時段為年徑流，校核資料個數5，預報數值1，依次點擊輸入資料、計算、顯示預報結果、顯示預報圖形，即可得到預報結果，如圖1。

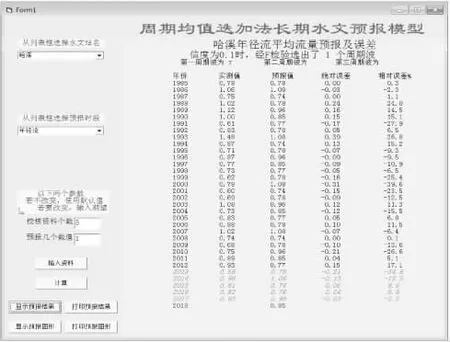
圖1 預報結果

3.2 ARIMA模型演算

打開SPSS數據編輯器導入數據，修改變量名稱，輸入預報年份。

點擊分析→預測→創建模型，打開時間序列建模器，自變量“年份”，因變量“年徑流量”，方法選擇“ARIMA”，選擇模型參數，如圖2。

圖2 選擇模型參數

分別選擇模型參數（p，d，q）為（1，1，1）、（1，1，2）、（1，1，3）、（1，1，4），點擊繼續，開始預報調試。

四種參數條件下的演算結果如表1。

表1 不同參數演算結果及誤差 單位：億m3

4 預報結果分析及徑流年內分配

4.1 演算分析

根據《水文情報預報規范》要求，“內陸及干旱地區水量預報的許可誤差，取實測值的20%，枯季月徑流預報的許可誤差，取實測值的30%”、“甲等：合格率≥85%；乙等：85%＞合格率≥70%”，判定周期均值迭加法合格率80%，屬乙等預報方案；參數選擇（1，1，4）情況下ARIMA模型合格率100%，但整體預報結果趨勢與實際來水趨勢不吻合，參數選擇（1，1，3）時，除枯水年不合格外，其他年份誤差較小，并且趨勢與實際情況較為吻合，故選擇參數為（1，1，3）的 ARIMA 模型，此時合格率 80%，也屬乙等預報方案。

周期均值迭加法2018年年徑流預報結果為0.85億m3，ARIMA模型預報結果為0.76億m3。

兩種方法均存在極端枯水年預報誤差過大問題，應根據預報當年的前期降水量判斷是否為極端枯水年，若為極端枯水年應當引入枯水修正系數。

4.2 枯水修正

在完成周期均值迭加預報和ARIMA模型預報的基礎上，繪制1985年～2017年徑流量與1月～6月降水散點圖，分析發現峽門河存在兩種明顯的枯水現象：①1月～6月降水量80mm～95mm時，年徑流量在0.6億m3左右，稱枯水現象A；②1月～6月降水量120mm～130mm時，年徑流量在0.7億m3左右，稱枯水現象B，見圖3。

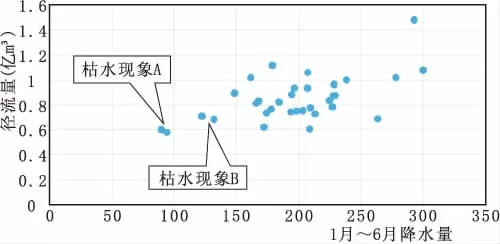
圖3 降雨徑流散點圖

普遍地，當降水量符合枯水現象A時，對周期均值迭加預報結果乘以枯水修正系數kA1，kA1結合2013年預報誤差取0.74，對ARIMA模型預報結果乘以枯水修正系數kA2，kA2結合2013年預報誤差取0.79。同樣，當降水量符合枯水現象B時，對周期均值迭加預報結果乘以枯水修正系數kB1，kB1參照枯水現象A和比例關系取0.89，對ARIMA模型預報結果乘以枯水修正系數kB2，kB2參照枯水現象A和比例關系取0.95，詳見表2。

表2 枯水修正系數取值

哈溪站2018年1月～6月自記雨量計實測降水量為85.8 mm，符合枯水現象A，判定2018年為極端枯水年，因此由周期均值迭加法預測2018年峽門河來水量為0.6290億m3，ARIMA模型預測結果為0.6004億m3。

4.3 重現期確定

根據33年來水資料序列繪制峽門河年徑流頻率曲線，確定2018年來水重現期，如圖4。

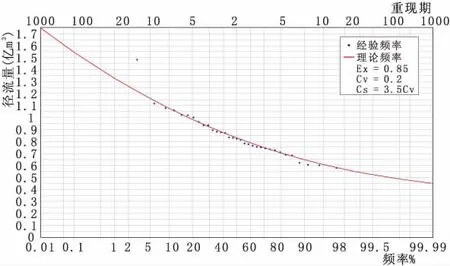
圖4 峽門河年徑流頻率曲線圖

枯水適線采用“就低”原則，周期均值迭加預報來水量0.6290億m3代表頻率92.3%，重現期為13年；ARIMA模型預報來水量0.6004億m3代表頻率95.7%，重現期為23年。兩種預報結果在實測序列中分別排第5位，第2位，屬極端枯水年，預報結果與石羊河流域整體豐枯趨勢一致。

4.4 徑流年內分配

根據前期降雨徑流和枯水修正選擇枯水現象A中的代表年2001年作為年內分配的模板，等比例分配，如圖5。

由徑流年內分配可知，5月～10月徑流量占全年78%以上，下半年徑流量占全年71%以上，來水高度集中。

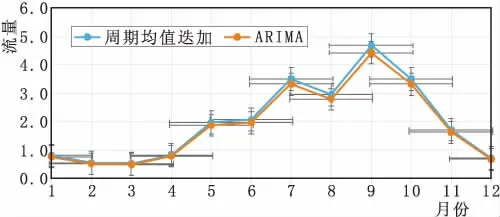
圖5 預測2018徑流年內分配

5 結論與建議

5.1 結論

1）鄰近值對周期均值迭加預報結果影響較大，序列均值對ARIMA模型預報結果影響較大。

2）直接使用預報軟件，兩種方法都有80%的合格率，能較好地契合峽門河實際水情，但都不能滿足枯水年預報精度要求。豐枯程度不同，需要引入不同的枯水修正系數進行枯水修正。

3）除枯水年，兩種方法的預報精度也存在差異。偏豐水年周期均值迭加法預報精度明顯高于ARIMA模型，平水年ARIMA模型預報精度高于周期均值迭加，但均在10%以內。

4）周期均值迭加需要判定周期是否顯著，如果數據序列較短，無法判定周期或顯著周期不存在，則周期均值迭加不能使用，同時不同豐枯情況兩種預報方法預報精度不同，因此在預報中應當采用盡可能多的資料相互印證。

5.2 建議

經前期降水、預報分析，2018年屬極端枯水年，預測峽門河來水量較多年均值偏少二到三成，可能對經濟發展產生不利影響，建議相關部門參考預報結果，根據雨水情變化、下游黃羊水庫蓄水情況、農田土壤墑情和沿線哈溪鎮與黃羊鎮城鄉供水情況，加強旱情監測，儲備抗旱物資，必要時開展人工降雨作業，最大程度降低旱情影響，同時注意防范可能出現的短時強降水。