基于FPGA的工業機器人運動控制器設計

劉宏樂，李 兵

(1.華北理工大學，河北 唐山 063210；2.唐山學院，河北 唐山 063000)

0 引言

隨著電子技術與信息技術的不斷發展，機器人正在逐漸地進入到工業領域中，尤其是在高端制造業和工業自動化生產中發揮著重要作用。運動控制系統是工業機器人的核心，它向驅動裝置發出任務信號，控制末端的執行裝置實現對被控對象的位置、速度等參數的精準控制。為此，就需要設計一個行之有效的運動控制器對給定軌跡進行實施跟蹤。

根據控制器控制核心的不同，運動控制器主要有三大類型：PC型、嵌入式型、全軟件型，并向多軸化、網絡化、開放式、智能化、可重構性等方向發展[1]。

依據運動控制器的上述類型及特點，為了達到良好的控制效果，專家們已經進行了很多的嘗試，在運動定位策略方面，根據不同的工況環境，有針對性地提出了決策樹、模糊邏輯、遺傳算法、人工神經網絡等智能算法與傳統PID相結合的方法[2]。傳統的PID控制因為結構簡單易懂，在大部分的工業自動化系統中都有它的存在，但是在碰到復雜的系統時，由于無法獲得準確的數學模型，難以整定PID的參數，因而無法獲得預期的效果。本文的研究對象為六自由度工業機器人，目前還無法建立準確的模型。考慮運算的實時性、控制的準確性、硬件設計的復雜性及可重構性，本設計選擇模糊PID作為運動控制器的核心算法。在運算的實時性方面，模糊算法實際上是一種離散的算法，無論選擇軟件執行還是硬件執行，在執行速度方面優于其他算法。因為模糊算法是一種經驗性算法，一般情況下決策樹、遺傳算法、人工神經網絡算法在運動控制的準確性方面要優于模糊算法，但如果模糊控制規則選擇得當，該算法也能夠滿足控制需求。在硬件設計的法則性方面，無論是采用PLC、單片機、DSP、嵌入式還是可編程邏輯芯片，模糊算法的實現都是最為容易的。在可重構性方面，如果采用的是純軟件設計方法(PC機)、PLC、單片機、DSP或嵌入式等方法，要根據重構需求重新修改軟件程序，同時還要更換相應的數據采集或通信接口等設備，成本比較高，周期也比較長[3]。如果采用的是FPGA，根據重構需求，通過修改程序即可設計出相應的電路系統，數據采集、通信接口電路的更改也可以通過修改程序來實現，可大大降低重構成本和周期。因此依托于FPGA設計模糊PID運動控制器更為簡單、易懂，開發周期更短，設計成本也更低。

1 伺服系統的傳遞函數

本設計中選擇的六自由度工業機器人為ABB的IRB-2600ID，在伺服電機的驅動下，相鄰的關節之間的動態性能可由下面的方程表示[4]：

(1)

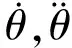
(2)

該微分方程即為六自由度工業機器人的傳遞函數。

2 模糊PID算法

由于六自由度工業機器人的伺服控制系統為非線性控制系統，傳統的PID控制在位置控制效果方面不能滿足要求，因此要將PID與模糊邏輯相結合對系統進行控制。模糊PID控制是根據PID控制器的3個參數與偏差e和偏差的變化ec之間的模糊關系，在運行時不斷檢測e及ec，通過事先確定的關系，利用模糊推理的方法，在線修改PID控制器的3個參數，讓PID參數可自整定[5]。在線實時調整控制器的kp，ki，kd這3個參數，得到整理后的Δkp，Δki，Δkd作為輸出。因為Δkp，Δki，Δkd這3個數一直是動態變化的，所以它們會根據系統的實時變化來整定自己的參數。PID控制參數的計算用到下列公式：

kp=kp0+Δkp

ki=ki0+Δki

kd=kd0+Δkd，

其中kp0，ki0，kd0為初始數據。

3 運動控制器的硬件實現

目前工業機器人的主流控制器有DSP、嵌入式、工控機、PLC等，這些控制器的結構與外設相對固定，使得控制缺乏靈活性，運算速率相對較低，實時性較差。雖然FPGA發展較晚，但它具有強大的計算能力及優異的可重構性，在控制器的開發設計以及升級改造等方面有著其他控制器無法匹及的優勢[6]。圖1為基于FPGA的模糊PID控制器電路結構。

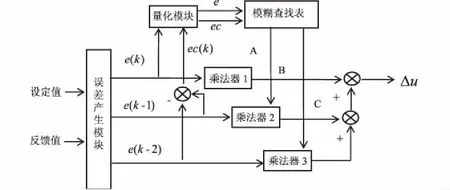
圖1 基于FPGA的模糊PID控制器電路結構

系統分為4個模塊：誤差產生模塊、量化模塊、模糊查找表模塊以及運算模塊。誤差產生模塊生成e和ec的精確值；量化模塊就是把精確的e，ec變成模糊值；模糊值進一步經過模糊查找表，輸出PID參數，最后通過一定運算，輸出最終的Δu值。本設計采用的FPGA型號為Altera公司的EP4CE40F29C8N。

3.1 誤差及誤差變化量模塊設計

本模塊的設計中輸入是誤差e以及誤差變化率ec，利用連續的兩個誤差e得到誤差變化率ec。整體設計采用的是原理圖設計方法，利用FPGA中固有的運算模塊來進行浮點運算，精確度更高，與傳統的編程語句實現方法相比較，該方法在消耗的硬件資源方面不占有優勢，但是在運算精度上卻要高出傳統方法。由于所選擇的FPGA具有豐富的邏輯單元，在電路結構上的消耗可以忽略。在時鐘CLK作用下同時將給定值與輸出反饋值送入兩個LPM_ADD_SUB模塊，同時接入兩個鎖存器，這樣送入第二個LPM_ADD_SUB模塊的值相對于第一個來說要差一個周期，那么兩個LPM_ADD_SUB模塊分別產生第k次和k-1次誤差。最后將這兩個誤差送入第三個LPM_ADD_SUB模塊中，輸出誤差變化量。在離散化論域中，誤差變化率的值通常是用誤差變化量的值來替代的。設計該模塊主要實現的是一個減法功能，于是調用了QuqrtusⅡ模塊庫中的LPM_ADD_SUB。圖2為誤差模塊設計原理圖。

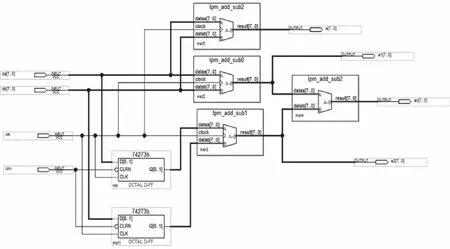
圖2 誤差模塊設計原理圖

3.2 模糊量化模塊設計

上一個模塊中輸出的e與ec是精確的量，但是模糊控制器的輸入是模糊值。為了得到模糊值就需要將精確值經過量化。設計此模塊，首先是將e與ec的模糊論域與實際論域根據實際情況設定出來；其次將模糊論域依據各個成分，把實際論域分成幾個段，每一段對應于一個模糊論域中的一個成分。劃分論域時，如果劃分過細，會造成規則數目太多而使得電路結構過于復雜，運算速度降低；如果劃分過粗的話，則無法達到精確的控制。IRB-2600ID型六自由度機械手臂的執行機構為伺服電機，由于伺服電機本身的控制為閉環控制，精度較高，因此在模糊論域的劃分上，權衡了控制精度與系統的復雜程度后，采用的是七級編碼機制，模糊語言變量劃分為7個以下論域集合{NB，NM，NS，ZO，PS，PM，PB}，即{負大，負中，負小，零，正小，正中，正大}，因此本文中將誤差大小量化為7個等級。當從現場采集到數值后，將機器人關節的旋轉角度誤差e與誤差變化率ec作為輸入。根據ABB IRB-2600ID工業機器人產品手冊可知，軸1的工作范圍是-180°～180°，因此將e與ec的實際論域范圍定為[-180，180]，量化因子為60，采取四舍五入的方式，把實際論域分成7段，分別是[-180，-150]，[-150，-90]，[-90，-30]，[-30，30]，[30，90]，[90，150]，[150，180]，對應到模糊論域范圍[-3，3]上，即{-3，-2，-1，0，1，2，3}。假設誤差的精確值是57，此精確值在[30，90]的論域段，誤差經過量化后的值就是1，量化地址為100。ec和e的量化過程相同，表1為e/ec的量化地址。

表1 模糊量化后的e/ec的量化地址

這部分采用VHDL語言進行設計，其部分代碼如下顯示：

PROCESS(E，EC，CLK)

BEGIN

IF CLK'EVENT AND CLK='1'THEN

IF E<=-180 THEN A<="111"；

ELSIF E>=-180 AND E<=-150 THEN A<="000"；

ELSIF E>=-150 AND E<=-90 THEN A<="001"；

ELSIF E>=-90 AND E<=-30 THEN A<="010"；

ELSIF E>=-30 AND E<=30 THEN A<="011"；

ELSIF E>=30 AND E<=90 THEN A<="100"；

ELSIF E>=90 AND E<=150 THEN A<="101"；

ELSIF E>=150 AND E<=180 THEN A<="110"；

ELSIF E>=180 THEN A<="111"；

END IF；

…

END IF；

END IF；

END PROCESS；

C<=A&B；

Q<=C；

END ART；

該模塊如圖3所示。

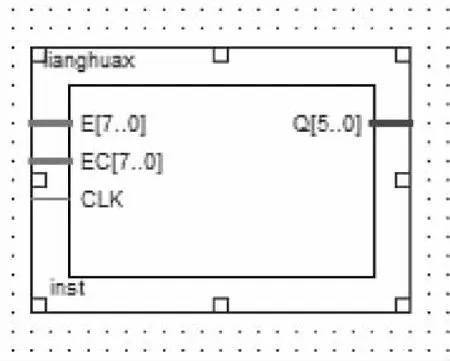
圖3 量化模塊

3.3 模糊查找表模塊設計

模糊控制器中，模糊查找表是至關重要的。由于在現實中模糊化運算、模糊推理和清晰化計算是非常繁復的，在線的演算量較少，故本文主要運用離線運算方式，這種方式不僅改善了FPGA的工作效率，而且編程的困難也有所消減。

為了得到Δkp，Δki，Δkd的值，主要通過Matlab建立模糊PID模型，在Matlab中得到相應的值。為了減少難度，可設A=Δkp+Δki+Δkd，B=-(Δkp+2Δkd)，C=Δkd。

通過計算得到以e和ec為輸入，以A，B，C為輸出的表格。高3位是e的量化地址，低3位是ec的量化地址。表2-表4即為A，B，C的模糊控制表。

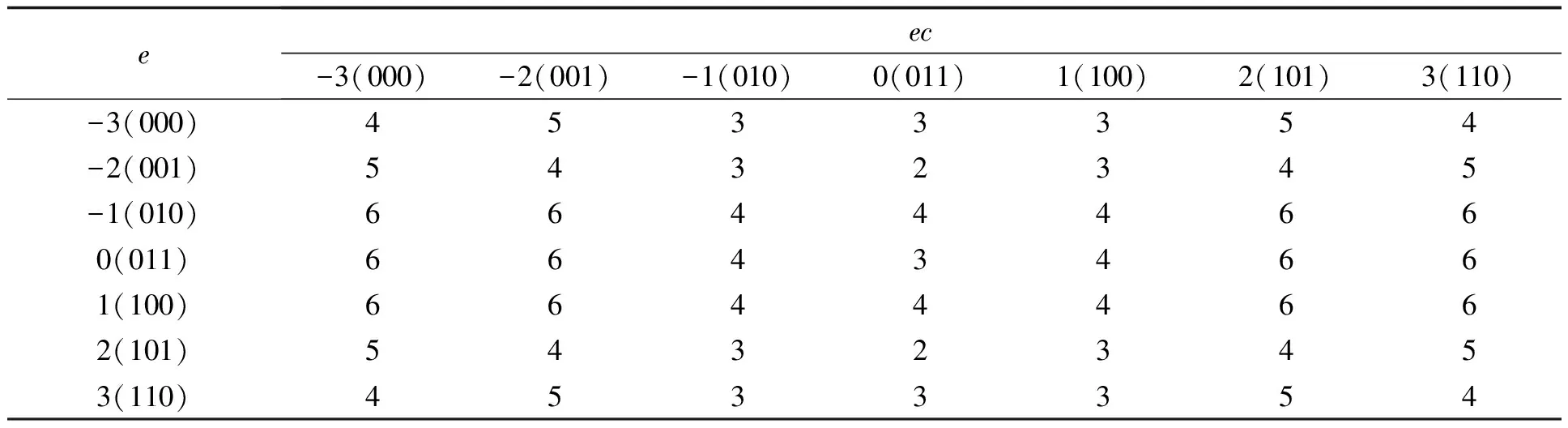
表2 A模糊控制表

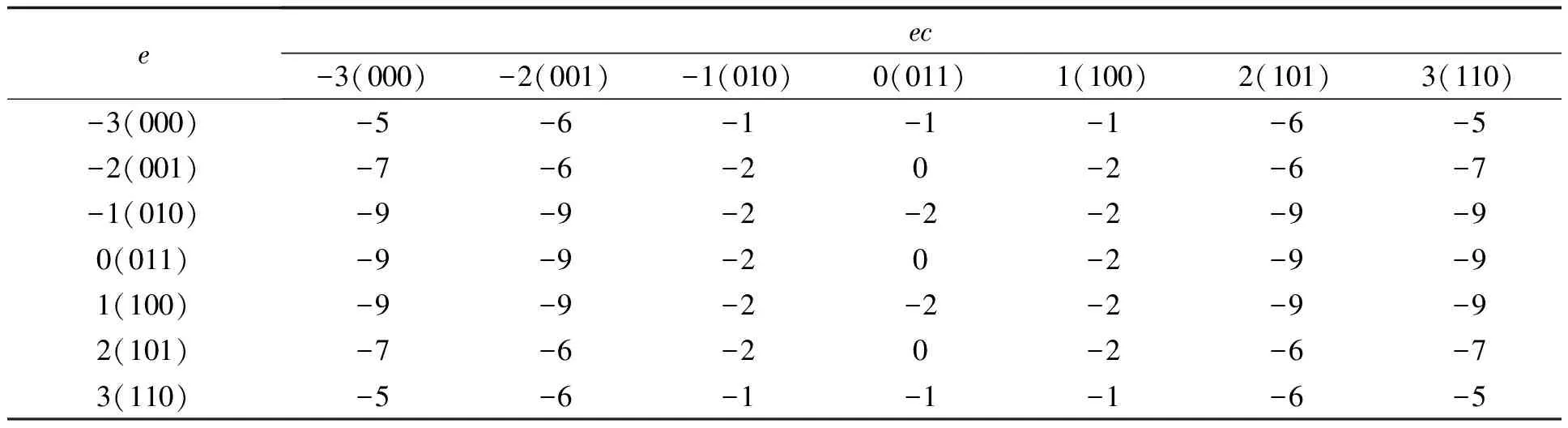
表3 B模糊控制表

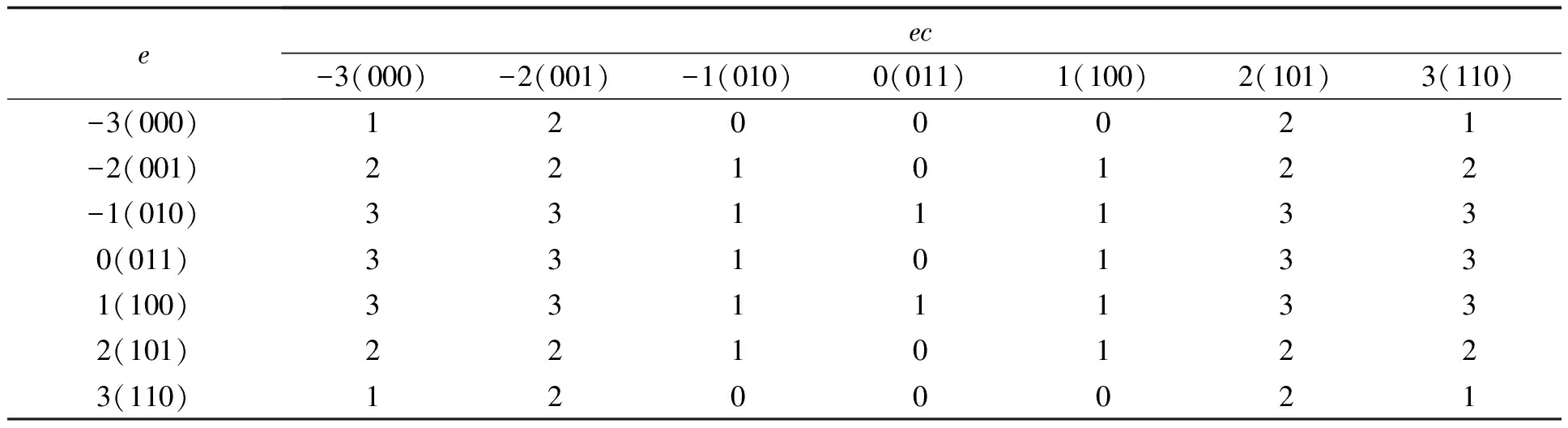
表4 C模糊控制表

為了更好地運用A，B，C模糊控制表，需要將它們制作成ROM模塊，而ROM模塊的核心就是MIF文件。將這些設計完后，此時只需要計算：

Δu(k)=Ae(k)+Be(k-1)+Ce(k-2)。

(3)

圖4為A的MIF文件。

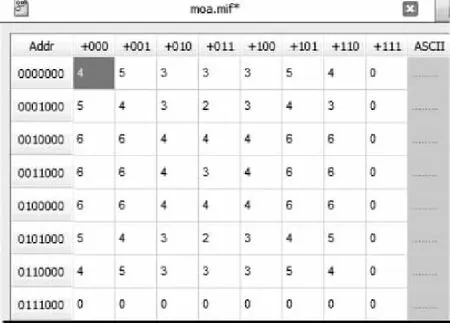
圖4 A的MIF文件

3.4 運算模塊設計

乘法運算模塊調用了函數庫里的LPM_MUITA。讓e(k)，B與e(k-1)，C與e(k-2)相乘，進一步使用parallel_add，使這3個參數通過加法功能獲得最后的結果Δu。圖5為運算模塊原理圖。

3.5 頂層模塊設計

圖6就是模糊PID算法的頂層模塊。首先輸入通過誤差模塊獲得的精確值，量化模塊把e和ec進行量化，得到模糊值；其次將量化后的值送入到下一個單元以查表的方式進行離線查詢，得出控制參數的增量；最后將計算得到的3個參數A，B，C輸入到下一個模塊，通過計算得到輸出。

取一組數據，如da=11，db=9，則可以得到e=2，e1=2，e2=5，ec=-3，e精確值是2，屬于[-180，180]這個論域，其量化值是0，量化編碼是011。同理可得ec的量化編碼是011。把e的量化編碼設為高3位，ec的量化編碼設為低3位，查表可知A=3，B=0，C=0，通過公式(3)計算得到Δu=6。電路仿真結果如圖7所示。

4 結語

由電路仿真結果可以看出，電路運算結果與理論計算得出的結果是一致的，說明設計中所采用的方法能夠滿足控制需求。電路運行的延遲時間為11 ns，確保了執行的實時性。控制器整體占用FPGA資源的58.5%，確保了后續升級重構需求。

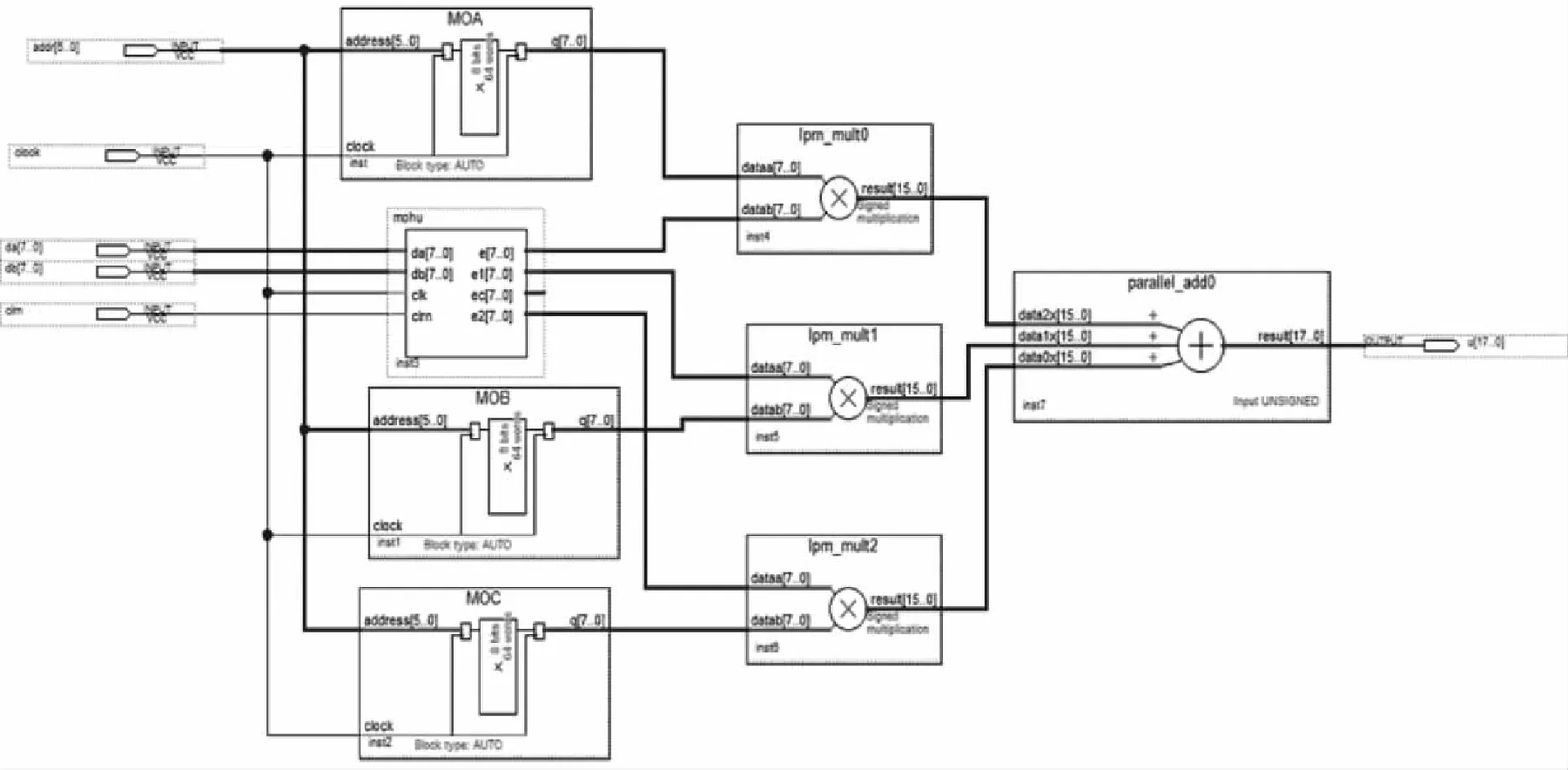
圖5 乘加運算模塊原理圖

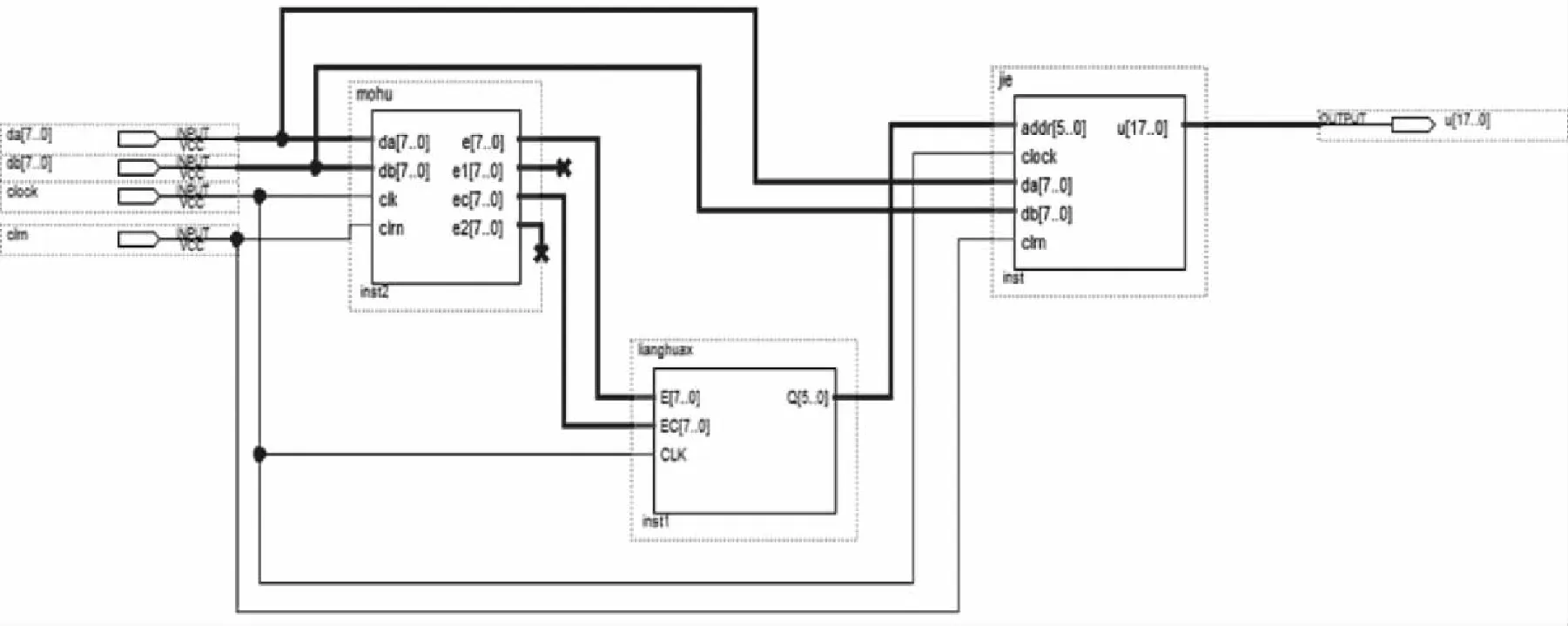
圖6 模糊PID算法頂層模塊

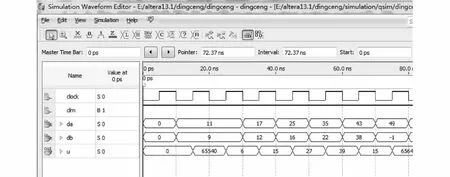
圖7 電路仿真結果