航天器多自由度太陽電池陣關節彈性載荷分析

張家雄，張華山，曹曉瑞，黃喜元，孫 光

（中國運載火箭技術研究院 研究發展中心，北京 100076）

0 引言

近年來，撓性太陽電池陣成為航天領域的研究熱點[1-2]。太陽電池陣具有面積大、剛度低、阻尼小的結構特點，導致其動力學特性復雜，一旦由于外界干擾力矩激勵起低階模態，輕則影響航天器正常工作，重則導致整個任務的失利[3]。因此，在設計階段建立太陽電池陣的精確動力學特性模型、開展彈性振動分析具有重要的現實意義。

航天器基頻遠高于太陽電池陣，故通常情況下在振動分析中可假定航天器本體為剛體，太陽電池陣為柔性體，建立剛柔耦合的動力學方程。該方法被廣泛采用，羅文采用混合坐標法對衛星-太陽電池陣進行剛柔耦合建模[4]；田強等采用絕對坐標方法表達機械臂-星體-太陽電池陣剛柔耦合多體系統的動力學特性[5]；張巍耀等通過有限元模型和Adams聯合仿真建立航天器-太陽電池陣剛柔耦合動力學模型，求取航天器姿態調整過程中太陽電池陣的動態響應[6]；馬鑫等采用梁、殼單元來模擬太陽電池陣結構進行有限元建模，并通過模態分析獲取太陽電池陣的模態特性，開展動力學仿真分析[7]。國內外學者對帶撓性附件航天器的動力學仿真研究較多[4,8-10]，特別是對于過度振動控制研究較為深入[11]，但對于太陽電池陣自身彈性載荷，特別是關節處的支撐載荷研究較少，而關節的載荷計算對關節電機的指標設計尤為重要。

本文針對多自由度太陽電池陣在航天器姿控發動機干擾力作用下產生彈性振動可能導致鎖止電機失效的問題，以遠距離操作工作模式為例，基于動力學模型開展動力學仿真，獲得太陽電池陣姿態運動信息和廣義坐標，進行太陽電池陣關節剛體、彈性載荷分析研究，以指導太陽電池陣的機構設計。

1 帶太陽電池陣航天器模型

1.1 帶太陽電池陣航天器幾何模型

典型的帶太陽電池陣航天器幾何模型如圖1所示，太陽電池陣基板及其展收機構通過O點與航天器連接；在軌運行過程中太陽電池陣需要實現對日定向，因此其基板需要以A點為中心繞x軸和y軸旋轉，A點需要配置機械鎖定機構以確保太陽電池陣在航天器本體運動產生的慣性載荷下保持展開姿態的穩定。此外，航天器姿態穩定控制過程中可能激勵起太陽電池陣的彈性模態，導致額外的慣性力。因此需要計算太陽電池陣以A點為中心繞x軸和y軸旋轉的慣性載荷，包括剛體運動載荷和彈性振動載荷，以便為A點鎖止電機的設計提供輸入條件。

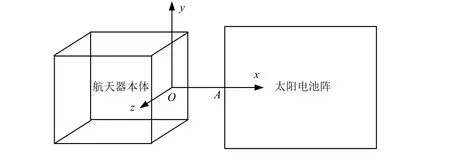
圖1 帶撓性太陽電池陣的航天器模型Fig.1 Spacecraft model with solar panels

1.2 太陽電池陣有限元建模及模態分析

對太陽電池陣結構進行有限元建模，基板采用殼單元模擬，展收機構采用梁單元模擬，將太陽電池陣上的電池片等主要模擬質量用非結構質量附加在殼單元上，最后采用局部質量點單元對太陽電池陣整體質量特性進行配置使其滿足要求，形成的太陽電池陣有限元模型如圖2所示。

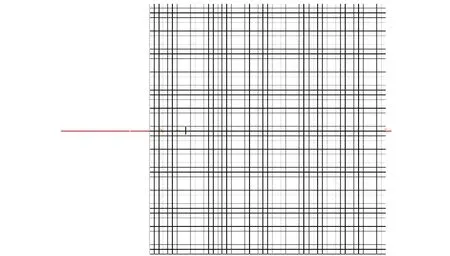
圖2 太陽電池陣有限元模型Fig.2 Finite element model for the solar panel

采用MSC.NASTRAN的103求解器對太陽電池陣有限元模型進行模態分析，獲取其模態特性，結果如圖3所示，太陽電池陣一階模態0.47 Hz，繞x軸旋轉；二階模態0.89 Hz，繞y軸旋轉。本文給出太陽電池陣根部固支狀態模態頻率10 Hz以下的共12階模態，作為航天器-太陽電池陣剛柔耦合動力學仿真的輸入。

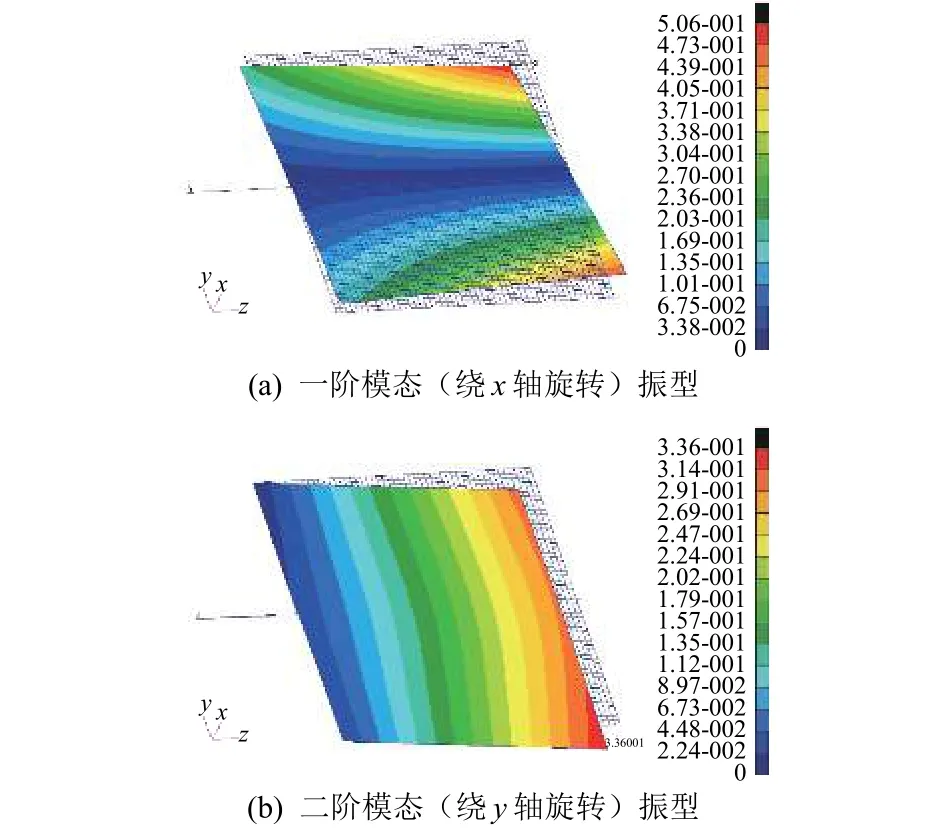
圖3 太陽電池陣模態特性Fig.3 Modal analysis for the solar panel

2 動力學分析模型

2.1 多自由度太陽電池陣航天器動力學方程

一般假設航天器為剛體，撓性附件太陽電池陣變形很小，采用矢量表達的航天器動力學方程可以簡化為：

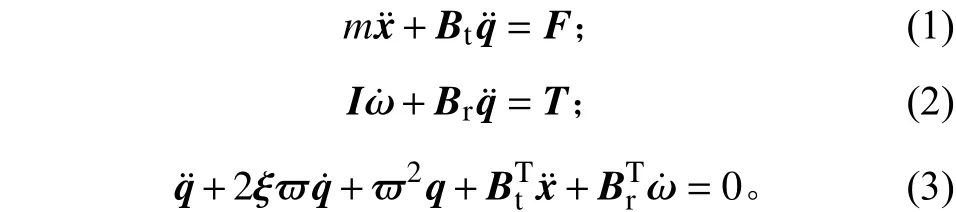
式中：m為 航天器總質量；為航天器加速度矩陣（3×1）；Bt為太陽電池陣平動耦合系數矩陣（3×n）；q為模態廣義坐標（n×1）；為模態廣義速度（n×1）；為模態廣義加速度（n×1）；F為控制力矩陣（3×1）；I為航天器慣量矩陣（3×3）；為航天器角加速度矩陣（3×1）；Br為太陽電池陣轉動耦合系數矩陣（3×n）；T為控制力矩矩陣（3×1）；ξ為阻尼系數矩陣（n×1）；?為模態頻率（n×1）；n為模態階數。

2.2 太陽電池陣關節剛體載荷

將整個太陽電池陣離散成M個dm質量點，根據點的相對運動求解每個點的慣性加速度，點乘質量矩陣得到每個點的慣性力，然后叉乘位移矢量可得到關節的剛體載荷。圖4為太陽電池陣任一點dm的運動示意：Oxyz為慣性靜坐標系，O′x′y′z′為動坐標系，O′x′y′z′相對Oxyz的位移矢量為、速度矢量為v0、加速度矢量為a0；點dm相對O′x′y′z′的位移矢量為r′、速度矢量為v′、加速度矢量為a′、角速度矢量為ω′、角加速度矢量為，相對Oxyz的絕對位移矢量為rm、速度矢量為vm、加速度矢量為am。

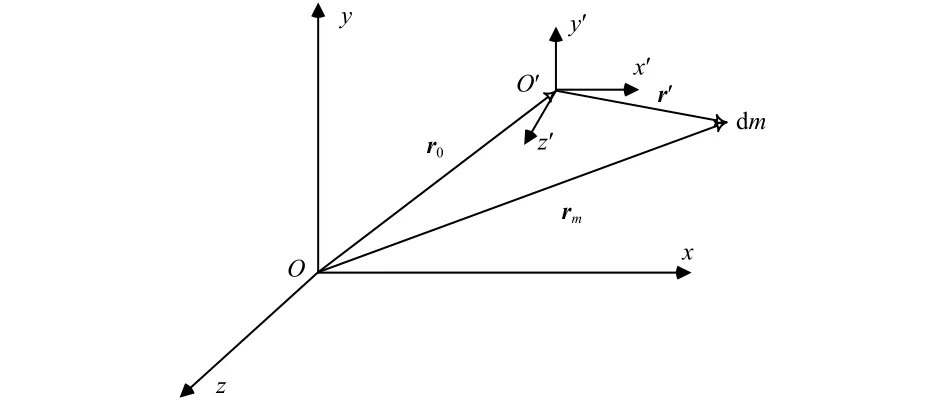
圖4 太陽電池陣任一點相對運動示意Fig.4 Relative motion for any point on the solar panel

根據位移矢量和

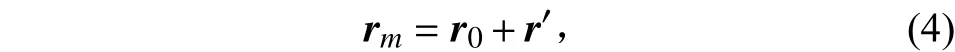
求一階導數得

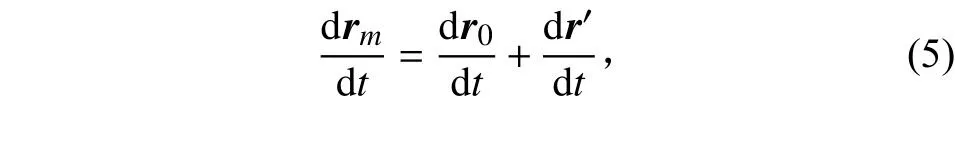
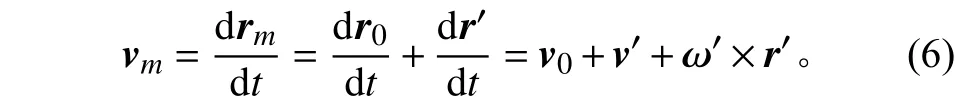
對式(5)求二次導數，

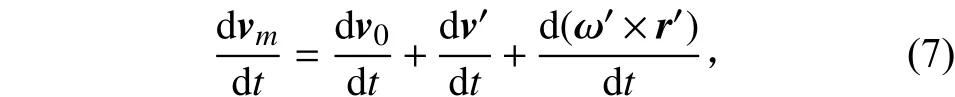
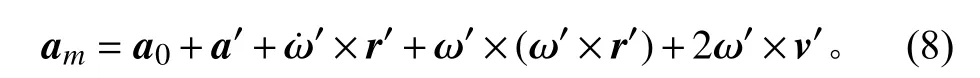
由于太陽電池陣與航天器固連，v′=0、a′=0，所以考慮剛體運動狀態下，動點dm相對靜系Oxyz的絕對加速度為

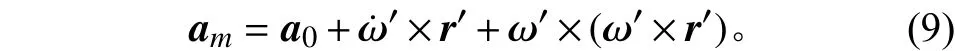
太陽電池陣關節的剛體載荷為

式中l為動點dm到關節點A的位移矢量。

2.3 太陽電池陣關節彈性載荷

考慮質點dm的彈性，dm發生振動變形后相對彈性系Oexeyeze的位移矢量為re、相對速度矢量為ve、相對加速度矢量為ae。不考慮dm相對彈性系Oexeyeze的轉動量，太陽電池陣任一點的相對運動如圖5所示。

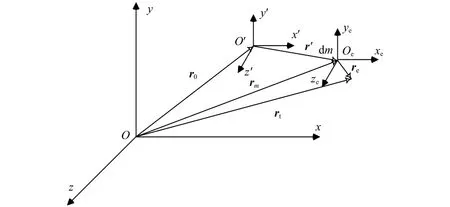
圖5 考慮彈性振動的太陽電池陣任一點相對運動Fig.5 Relative motion for any point with consideration of elastic vibration

已知i階模態廣義坐標和模態振型Φi，re、ve、ae與qi、Φi的關系式為

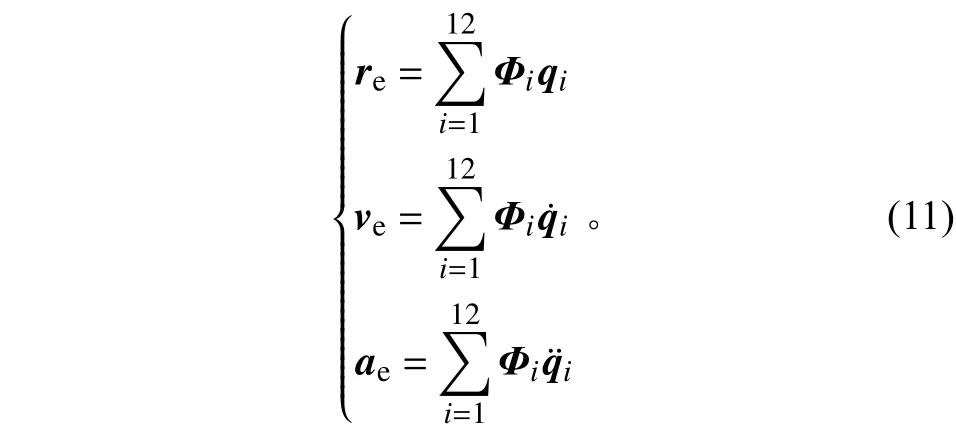
與式(4)同理，

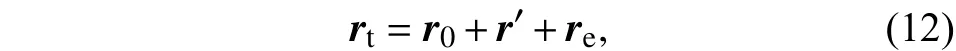
求2次導數后，考慮太陽電池陣彈性狀態下，動點dm相對靜系Oxyz的絕對加速度為

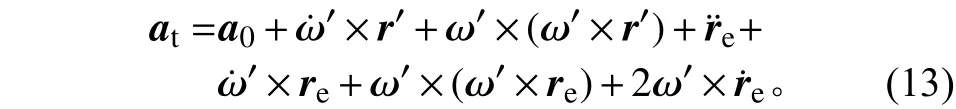
忽略式(13)中的二次項，可將其簡化為

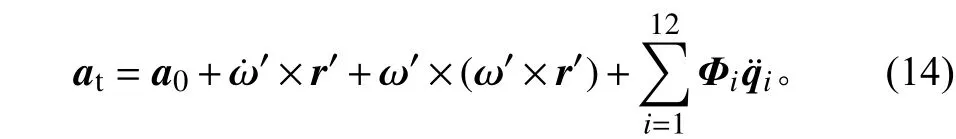
太陽電池陣關節的彈性載荷為

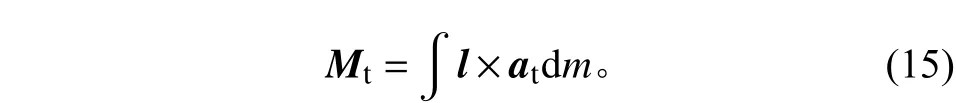
3 仿真分析結果

3.1 仿真參數

取頻率小于10 Hz的前12階模態，根據以往經驗將模態阻尼取為0.005。

3.2 模態廣義坐標

圖6為仿真計算得到的前12階模態廣義坐標，由圖可知，前3階響應較大，第4～第12階模態響應較小，基本可以忽略。

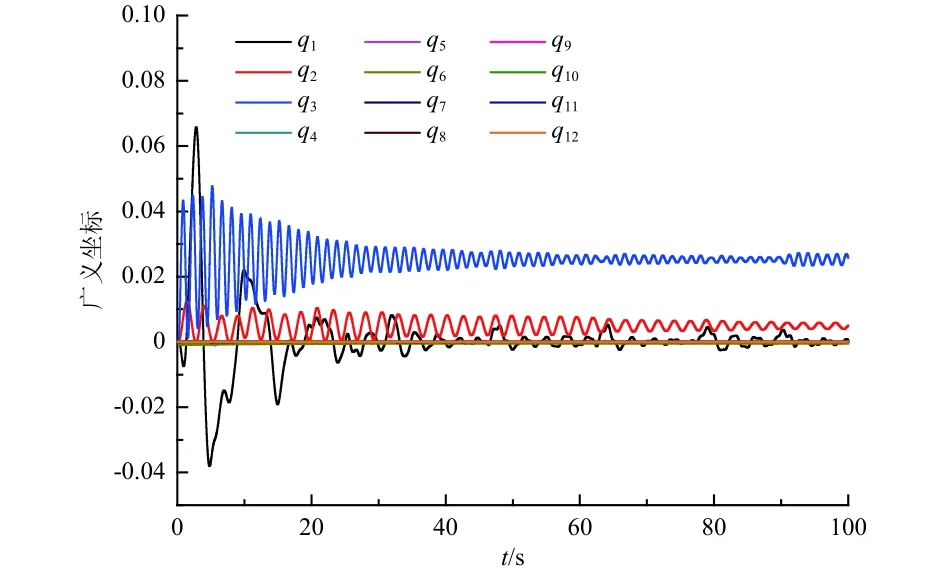
圖6 前12階模態廣義坐標Fig.6 The modal coordinates of the first 12 orders

3.3 剛/彈載荷計算

根據式(10)和式(15)計算得到A點的x向和y向鉸鏈力矩Mx和My，如圖7和圖8所示。由圖可知，彈性載荷大于剛體載荷的計算結果，且從趨勢來看，彈性載荷以剛體載荷計算結果為中心線上下振蕩，這與外界干擾力激勵起低階模態有關。

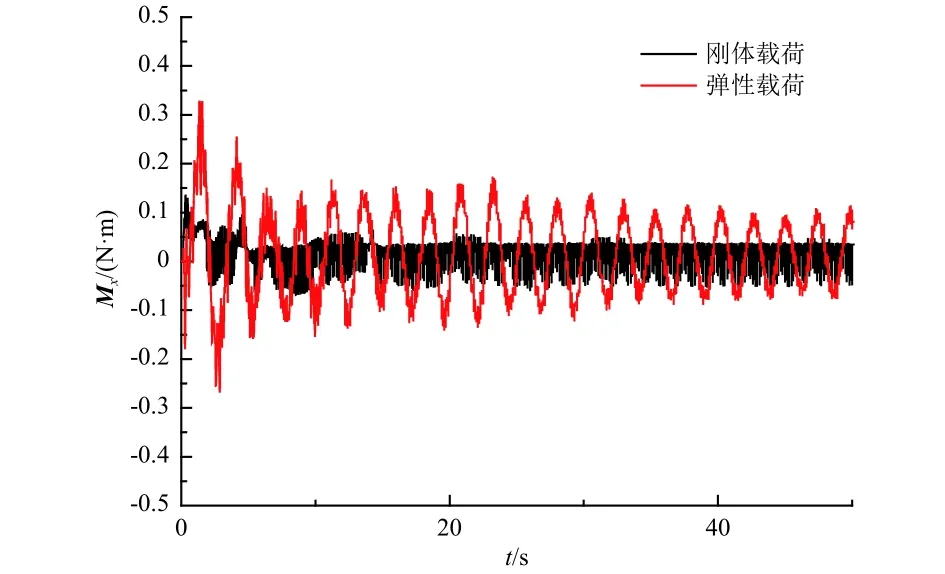
圖7 A點Mx剛體和彈性載荷計算結果對比Fig.7 Rigid and elastic load analysis of Mx for point A

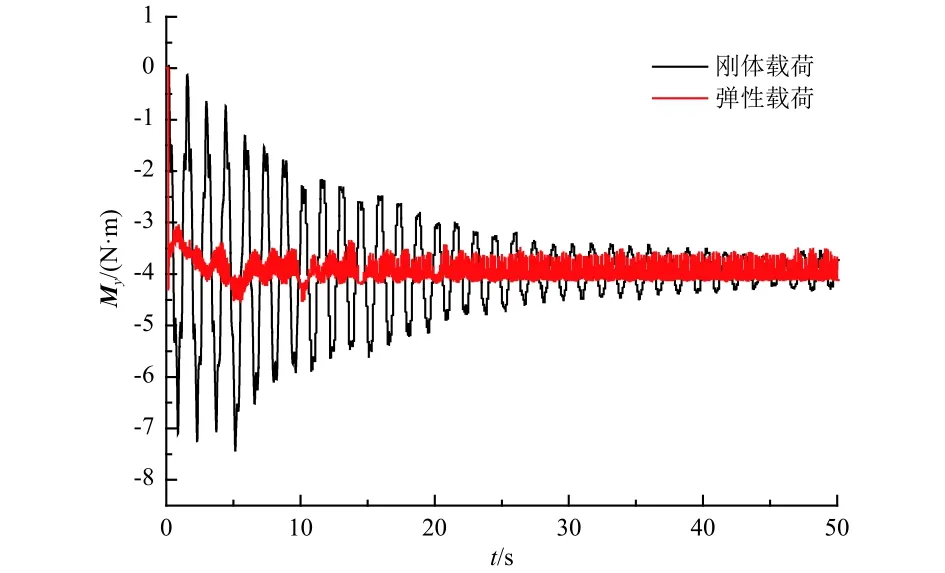
圖8 A點My剛體和彈性載荷計算結果對比Fig.8 Rigid and elastic load analysis of My for point A

4 結論

本文通過對航天器太陽電池陣模型的簡化，著重考慮機構及連接結構剛度的模擬和整體質量特性模擬，建立太陽電池陣有限元模型以及動力學分析模型，開展動力學仿真，求解太陽電池陣關節處的剛體載荷和彈性載荷，得到主要結論如下：

1）從模態廣義坐標仿真結果來看，前3階模態響應較大，高階模態響應較小，基本可以忽略；從各階模態彈性振動的收斂情況來看，未出現彈性發散的現象。

2）彈性載荷大于剛體載荷的計算結果，且從趨勢來看，彈性載荷以剛體載荷計算結果為中心線上下振蕩，這與外界干擾力激勵起低階模態有關。

本文通過結合動力學仿真和工程算法求解太陽電池陣關節的彈性載荷，解決了太陽電池陣鎖止機構指標設計的難題，避免了以往采用剛體算法不精確的缺陷，確保了航天器在軌任務的可靠性。

需要說明的是，本文以遠距離操作工作模式為算例，實際彈性載荷計算過程中應該充分覆蓋航天器的所有工作模式，確保所有可能引起太陽電池陣彈性振動發散的外在因素都在考慮范圍之內。