高鐵再生制動工況下公用電網負序電流優化

羅 培，楊維民，張 敏

(湘潭大學 信息工程學院，湖南 湘潭 411105)

近年來，中國的高速鐵路有了快速發展,我國已成為世界上高速鐵路運營最快、里程最長的國家。高速鐵路因電力機車負載不平衡產生的負序電流問題卻日益嚴重。負序電流能夠引起電力系統發電機轉子過熱、振動，引起繼電保護裝置誤動作等一系列問題，給公用電網和列車的安全穩定運行帶來隱患[1]。為減少負序電流對電氣化鐵路的影響，國內外學者提出了一系列補償裝置[2-3]，其中較為典型的為采取靜止無功補償器(Static Var Compensator, SVC)[4]、靜止無功發生器(Static Var Generator, SVG)[5]、鐵路功率調節器(Railway Power Controller, RPC)[6]等方法。由于能平衡2個供電臂之間的有功功率，采用RPC在治理負序電流問題表現出良好的應用前景。

文獻[7]著重分析了負序電流產生機理，并對牽引工況下負序電流給出了計算和分析，文獻[8]提出基于潮流控制器(Power Flow Controller,PFC)的補償方法，能有效抑制負序電流，但這些研究并未考慮列車制動情況下的補償，實際上高速交流傳動電力機車在制動過程中會產生很大的再生制動能量[9-10]。目前高速鐵路產生的再生制動能量主要包含2種利用途徑：第1種是通過功率轉移到另一供電臂被正在牽引運行的高速列車所吸收；第2種是直接通過牽引變壓器反饋給公用電網，這種方法將增加公用電網的負序電流，在反饋的再生制動能量較大時可能對公用電網中的其他設備產生影響。目前沒有關于高速鐵路牽引供電系統在再生制動工況下的負序電流補償相關文獻。

超級電容(Super Capacitor, SC)具有快速充放電、低污染、高效率等特點而廣泛應用于城軌列車系統和地鐵系統[11]，為解決高速列車再生制動工況產生巨大能量流入公用電網造成負序電流急劇增加的問題，本文提出一種基于SC儲能的鐵路功率調節器(SC-RPC)，通過分析SC-RPC牽引工況和再生制動工況的電氣模型，推導出公用電網負序電流的表達式，并提出SC-RPC的約束條件，采用改進粒子群算法求解，以負序電流最小為目標函數，各項指標為約束，求解全局最優解。最后提出相應的控制策略，通過仿真實驗驗證了該方法的有效性。

1 SC-RPC結構

SC-RPC的結構如圖1所示。圖中：IA，IB，IC為變壓器一次側電流；UA，UB，UC為變壓器一次側電壓；Ia和Ib為變壓器二次側a，b供電臂電流；Iac和Ibc為a,b供電臂補償電流；IaL和IbL為a，b供電臂負載電流；Is為SC電流。

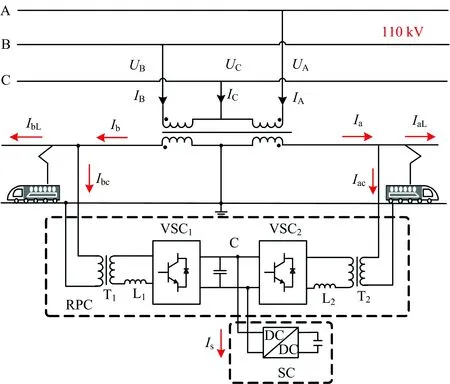
圖1 SC-RPC結構

由圖1可知，該系統包括V/v變壓器、RPC和SC，其中RPC由降壓變壓器T1和T2、單相電壓源換流器VSC1和VSC2、直流電容C及串聯電抗器L1和L2組成。SC主要采用雙向DC/DC變換器將產生的再生制動能量儲存到超級電容中，防止制動能量通過變壓器流向公用電網，從而降低公用電網的負序電流。

2 SC-RPC電氣模型

2.1 牽引工況下

牽引工況下SC-RPC單側供電臂的電氣模型如圖2所示。圖中：Ua為a供電臂電壓；Ra為a供電臂V/v變壓器等效電阻；La為V/v變壓器等效電感；RL為負載等效電阻；L為負載的等效電感；IaLp為a供電臂負載的有功電流；IaLq為a供電臂負載的無功電流；Iacp為a供電臂SC-RPC的補償有功電流；Iacq為a供電臂SC-RPC的補償無功電流。

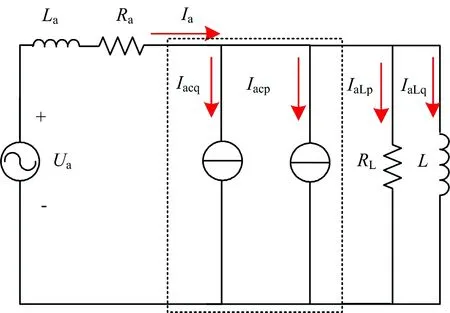
圖2 牽引工況下SC-RPC單側供電臂的電氣模型

牽引工況下SC不工作，RPC通過有功功率和無功功率補償對供電電網進行補償。關于牽引工況下RPC的補償，有大量文獻提出了很多方法，本文不再贅述。

2.2 再生制動工況下

再生制動工況下SC-RPC單側供電臂的電氣模型如圖3所示。再生制動工況下，列車制動產生再生制動能量，方向為從供電臂流向公用電網，此時SC工作。再生制動工況下，產生的再生制動能量若不能被轉移或存儲，就會流入公用電網，可能對公用電網中的其他設備產生影響。

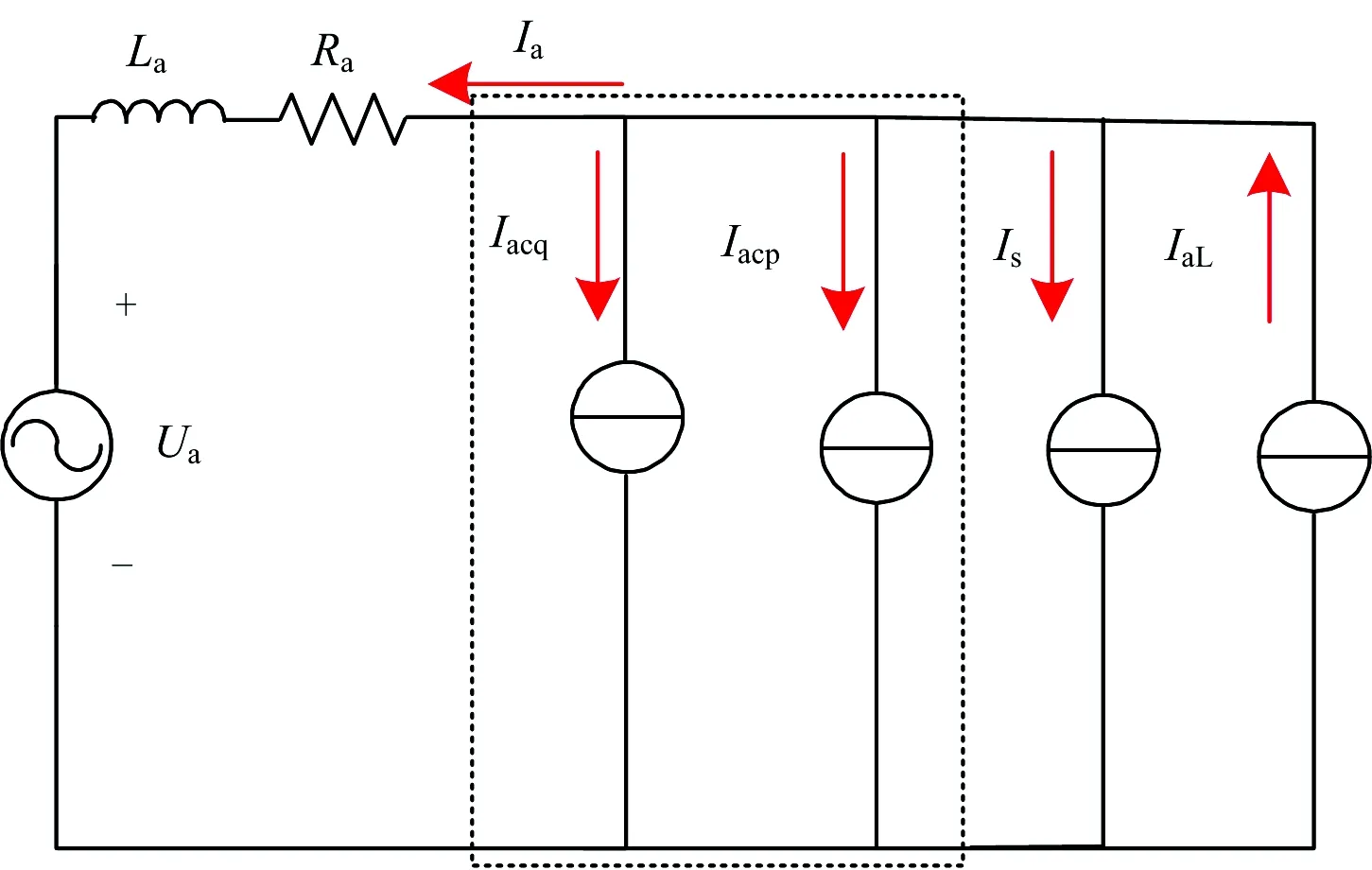
圖3 再生制動工況下SC-RPC單側供電臂的電氣模型

3 SC-RPC再生制動工況下最小負序電流數學模型

3.1 負序電流的表達式

SC-RPC再生制動工況下的向量圖如圖4所示。圖中：θa，θb分別為a，b這2個電臂的功率因數角；Ub為b供電臂電壓。a供電臂為牽引工況，電流IaL位于第四象限，b供電臂為再生制動工況，電流IbL位于第二象限。θb>π/2，表示b供電臂為再生制動工況，處于放電狀態。

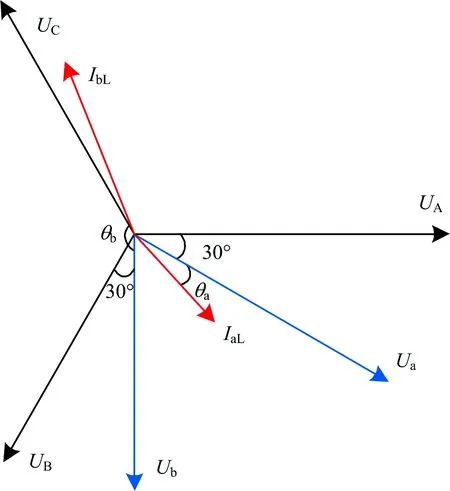
圖4 再生制動工況下的向量圖

補償前，公用電網的負序電流I-[7]較大，為

(1)

式中：K為變壓器匝數比。

由于并聯了SC，Ia，Ib，θa，θb和Is之間的關系為

(2)

式中：IbLp為b供電臂負載的有功電流；IbLq為b供電臂負載的無功電流；Ibcp為b供電臂SC-RPC的補償有功電流；Ibcq為b供電臂的補償無功電流。

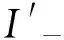
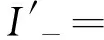
(IbLp-Ibcp-Is)2+(IbLq-Iacq)2+

(3)

3.2 約束條件

1)SC-RPC有功功率傳輸平衡限制

忽略損耗即SC-RPC不消耗有功功率，SC-RPC補償前后的有功功率是相等的。RPC補償的有功電流為ΔI，方向從b供電臂到a供電臂，則SC-RPC有功功率傳輸平衡限制為

ΔI=Iacp=-Ibcp

(4)

2)超級電容最大電流限制

(5)

3) 2個供電臂電壓波動范圍限制

牽引變壓器和牽引網線路的阻抗較大，列車負載的波動也非常大，所以牽引網電壓的過壓、欠壓對列車會產生不利影響。2個供電臂電壓波動范圍限制為

(6)

式中：Umax+為最大電壓的波動上限；Umax-為最大電壓的波動下限；ω為角頻率；Rb為b供電臂V/v變壓器等效電阻。

4)公用電網功率因數限制

根據國家標準，要求在牽引網高壓計量點處的三相電網功率因數pf不小于0.9，則公用電網功率因數限制為

Pf=[Ua(IaLp+Iacp)+Ub(IbLp-Ibcp-Is)]/{[Ua(IaLp+Iacp)+Ub(IbLp-Ibcp-Is)]2+[Ua(IaLq+Iacq)+

(7)

5)設備電流限制

由于電流限制，SC-RPC中Iacp和Ibcq的瞬時值都不能超過其限制值。假設SC-RPC最大電流為Icmax,最大傳輸有功功率為Pmax，則設備電流限制為

(8)

6)變壓器容量限制

由于變壓器容量的限制，a，b供電臂補償后的瞬時功率不能比單個線圈的額定功率大，則變壓器容量限制為

(9)

式中：Pa為變壓器額定功率。

3.3 SC-RPC負序電流優化數學模型

綜上可知，再生制動工況下的負序電流優化是1個多維、非線性約束的優化問題。SC-RPC補償后公用電網最小負序電流數學模型的目標函數為式(3)，約束條件為式(4)—式(9)。式(3)中，IaLp，IaLq，Iacp，Iacq為可測量參數，則該目標函數的決策向量為由ΔI，Iacq，Ibcq，Is組成的4維向量，即目標函數的求解由1個等式、10個不等式約束。

4 改進粒子群算法求解數學模型

目前求解多維非線性問題有很多，如模擬退火算法、遺傳算法、蟻群算法等。粒子群算法由于尋優能力強、收斂速度快等優點，在電力系統獲得越來越多的關注[12]。本文采用粒子群算法求解公用電網負序電流優化問題。

4.1 改進粒子群算法

粒子群算法中，粒子的全局搜索能力和當前的慣性權重取值密切相關，用wi(t)表示，取值的好壞，影響著算法的收斂性。常用的慣性權重取值是隨著迭代次數的遞增線性遞增或者遞減，該方法對慣性權重的取值缺乏指導。本文利用粒子與種群全局最優解的距離指導權重取值。

wi(t)=wmax-(wmax-wmin)(di(t)-1)2

(10)

其中,

式中：wi(t)為t時刻第i個粒子的權重；wmin和wmax分別為w的最小值和最大值；di(t)為t時刻第i個粒子與種群全局最優解的距離；xmax和xmin分別為粒子位置的最大值和最小值；D為解空間維數；xgj(t)為當前粒子t時刻全局最優解；xij(t)為粒子t時刻位置。

當粒子與全局最優值距離較大時，權重w取值較大，粒子全局搜索能力增強，當粒子與全局最優值距離較小時，權重w取值較小，提高了粒子局部搜索能力。

4.2 改進粒子群算法求解

改進粒子群算法求解最小負序電流數學模型時的具體流程圖如圖5所示。

5 SC-RPC再生制動工況下控制策略

5.1 SC-RPC控制結構

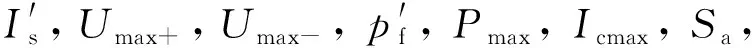
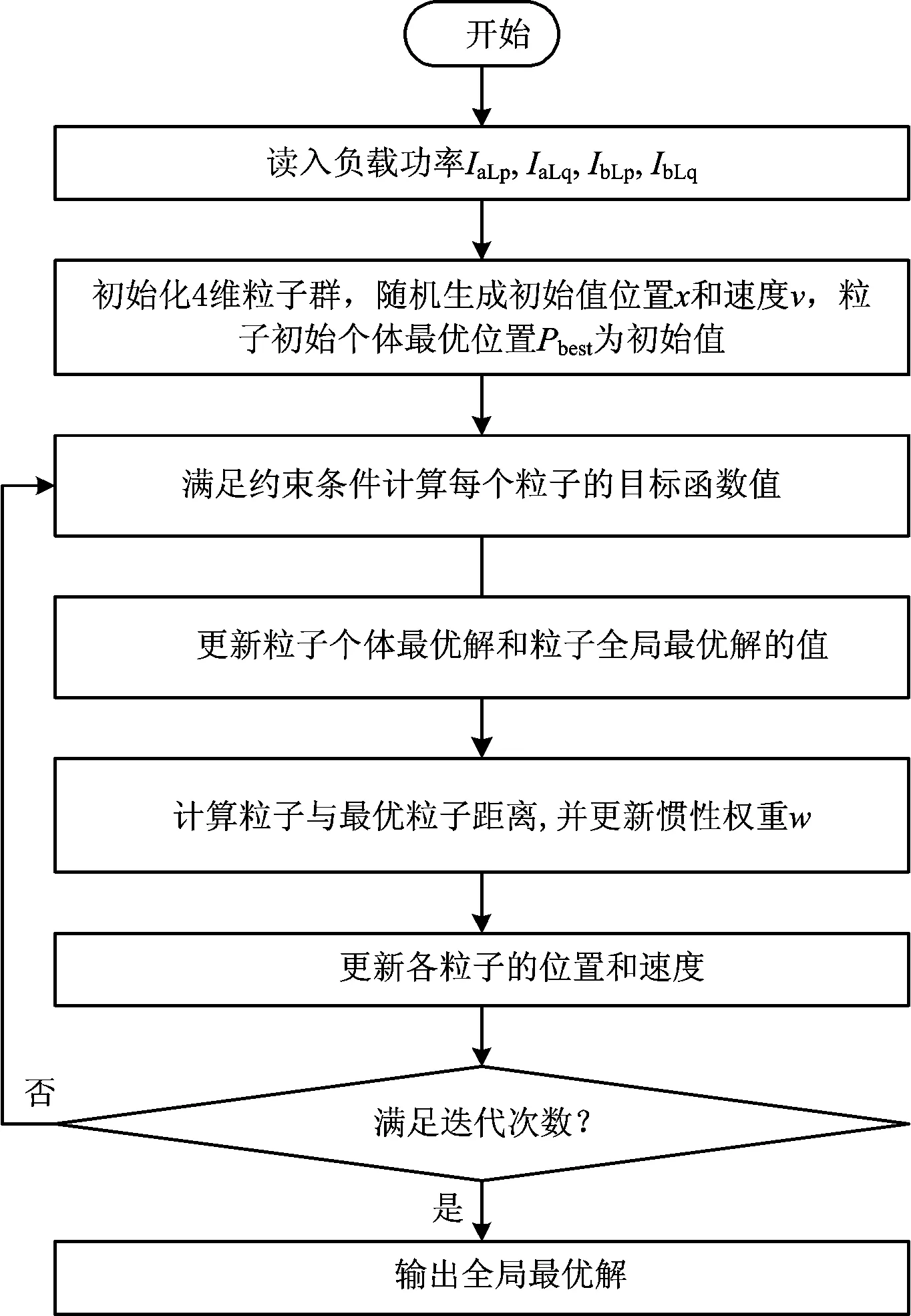
圖5 改進粒子群算法求解模型流程圖

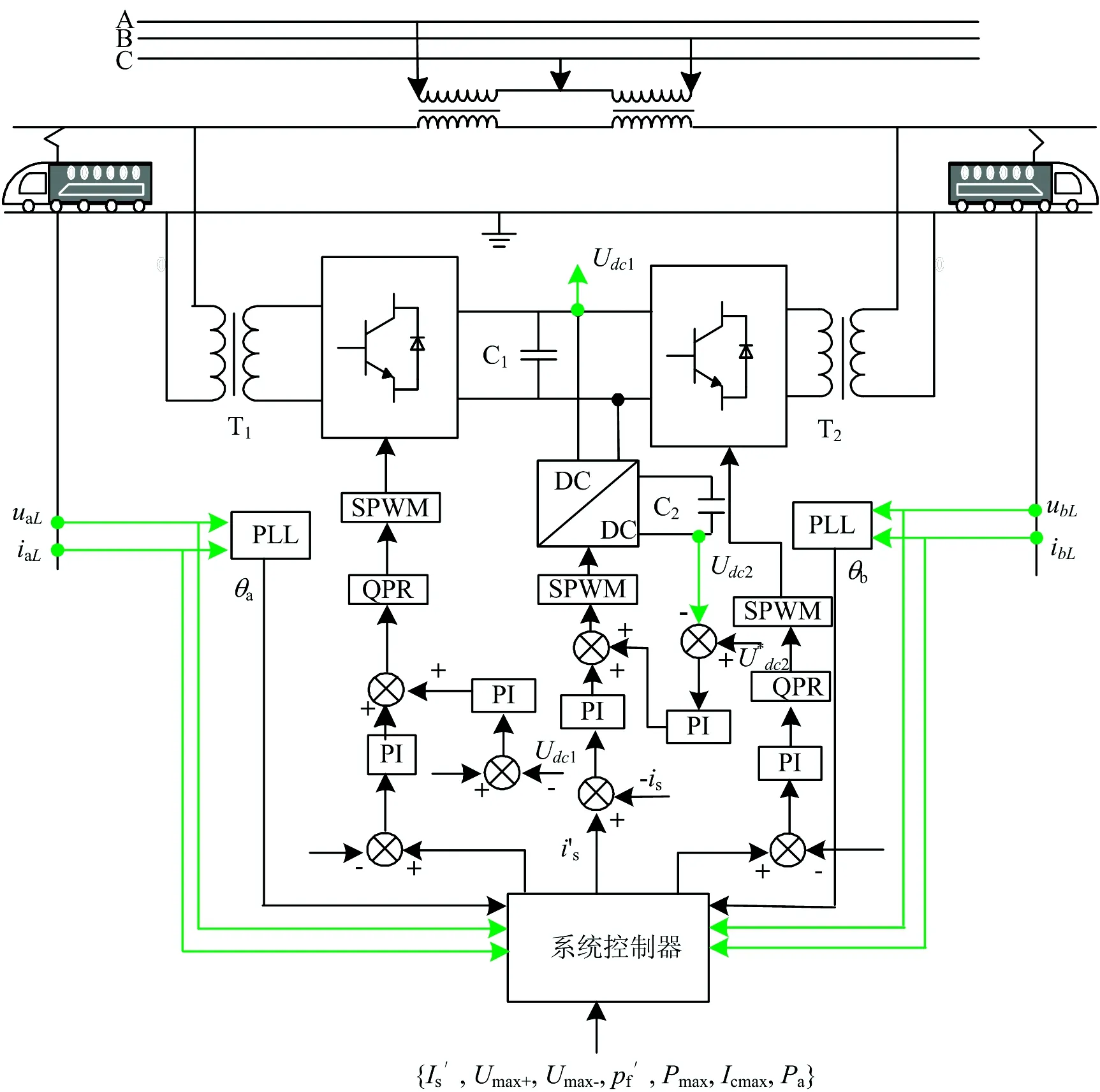
圖6 SC-RPC控制系統結構圖

5.2 RPC控制策略

5.3 SC控制策略

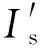
6 仿真驗證

為了驗證再生制動工況下SC-RPC負序電流優化方案的有效性，搭建Matlab仿真系統，參數見表1。

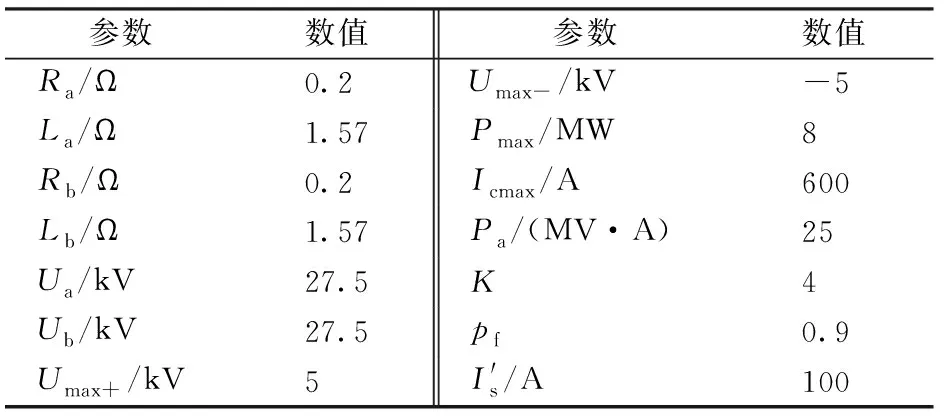
表1 牽引供電系統仿真參數

6.1 不同再生制動工況下的補償結果

為檢驗不同再生制動工況下本文方法的有效性，設置5種不同工況進行試驗。SC最大電流限制、2個供電臂電壓波動、功率因數、設備容量、變壓器最大容量見表2，最小負序電流優化補償效果見表2。

表2 優化補償效果

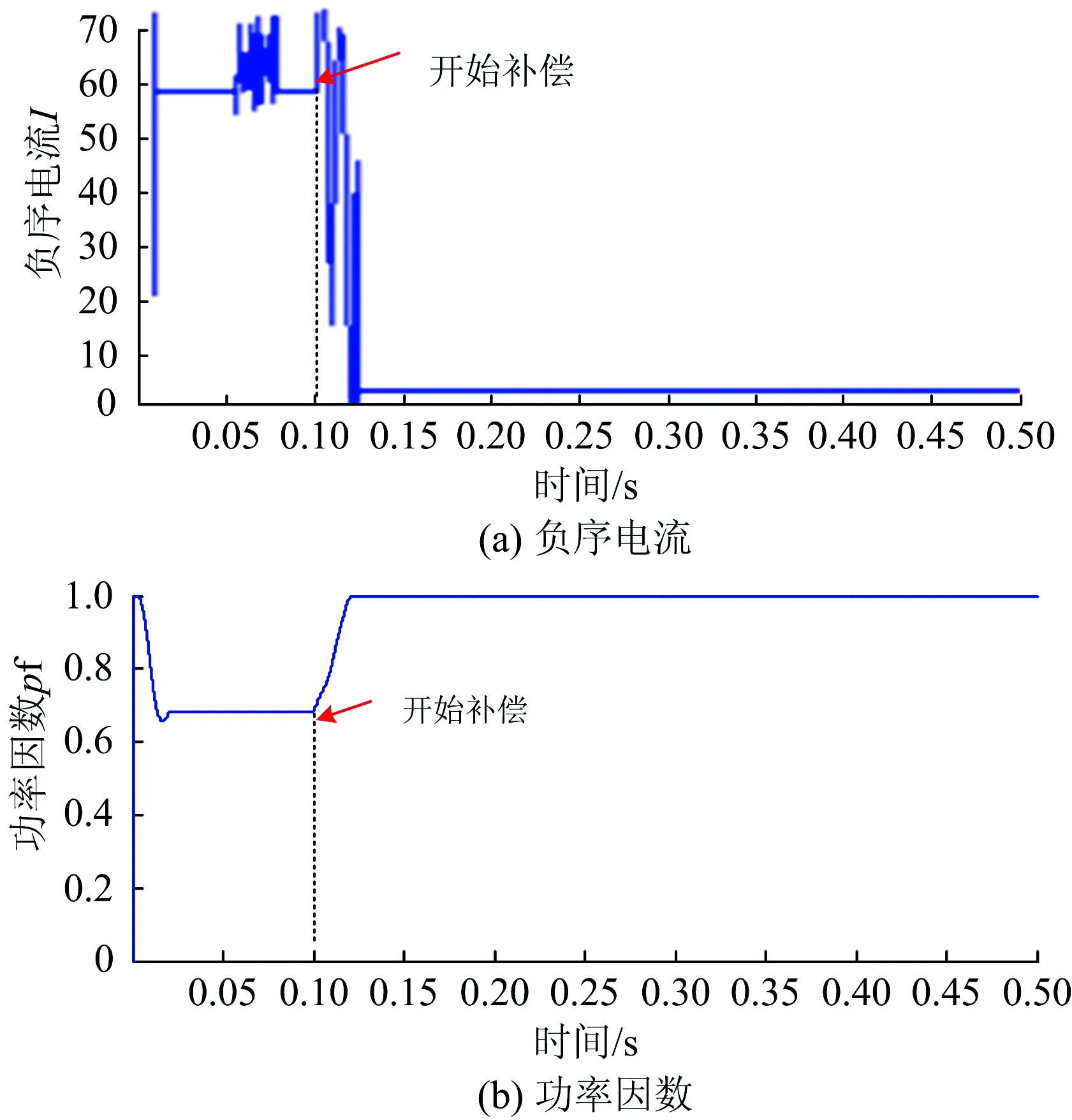
由表3可見：工況1下a供電臂中的再生制動能量一部分流向b供電臂，一部分被存儲在超級電容中，轉移的有功電流為122 A，超級電容的指令值最優值為68 A，補償后負序電流降低約92%，抑制效果明顯；工況2下-IaLp

6.2 補償結果的仿真驗證

為檢驗本文方法在有效降低負序電流的同時功率因數是否達標，對照圖1，利用Matlab構建仿真系統。仿真時間為0.5 s，在0.1 s采用SC-RPC進行補償。假設a供電臂為再生制動狀態，b供電臂為正常牽引狀態，IaLp=-150 A,IaLq=30 A,IbLp=130 A,IbLq=50 A。利用SC-RPC進行補償時，控制策略采用上文所述方法。

優化補償效果的仿真結果如圖7所示。由圖7可見：補償前負序電流為60.2A，補償后負序電流降低至4.3 A，降低約92%；與此同時，補償后功率因數達到電能質量要求(pf≥0.9)；仿真結果驗證了本文所提方法的有效性。

圖7 優化補償效果

7 結 語

通過建立SC-RPC再生制動工況的電氣模型，分析補償原理，構建了SC-RPC的最小負序電流數學模型，采用粒子群算法，通過自適應調整粒子的慣性權重，快速求解全局最優解，并提出相應的控制策略，最后通過仿真實驗驗證了該方法在再生制動工況下抑制公用電網負序電流的有效性。