基于I-GARCH的不確定時間序列概率分布推算

湯其婕，王 玙

(南京航空航天大學 計算機科學與技術學院，江蘇 南京 211106)

0 引 言

時間序列(time series)是一種典型的高維數據類型，其在傳感器網絡、位置定位服務(location based service，LBS)、環境監測、醫療檢測、物聯網等眾多領域應用廣泛[1-2]。但是，受數據采集設備的缺陷或者人為因素的影響，采集得到的數據在一定范圍內存在偏差。將這類型的數據定義為不確定時間序列(uncertain time series)。而針對不確定時間序列的有效存儲，到目前為止仍沒有良好的解決方案。

一種處理不確定數據最有效的方案是概率方法。近年來許多專家和學者提出了一系列的方法用于解決不確定數據的管理和查詢問題[3-9]。這些方法有一個共同特征，即假定用于進行查詢的概率數據是已知的，可以直接獲取到。但是，現實情況并非如此。不確定時間序列的概率是由推導出這些概率的概率分布函數決定的，這些概率分布函數以時間為坐標不斷發生變化。簡而言之，不確定時間序列的概率值隨時間不斷變化，無法得到其固定值，因此無法使用已有的概率數據庫生成方法直接對其進行存儲處理。因此，如何“創造”概率數據仍是未解決的問題，也是文中主要研究的問題。

針對從已知的時間序列推導得到時間序列的概率分布問題，文中主要完成的工作分為兩部分。一是依托已有的各種數學模型，結合已有的動態密度指標的概念，提出ARMA-GARCH動態密度指標模型，并對其推算原理進行了詳細的分析與介紹；二是針對GARCH模型無法高效處理含錯數據的弊端，提出改進的I-GARCH模型。該模型在處理含錯數據集時能體現出良好的容錯性，更符合一般的不確定時間序列數據的采集規律。最后通過實驗進行驗證。

1 相關工作

1.1 動態密度指標

時間序列由于依賴時間的變化，通常呈現出很大的不確定性，因此為不確定時間序列數據創建概率數據庫的最大挑戰之一是處理不斷更新的概率分布。如圖1所示，該圖為一天當中的氣溫隨時間的變化曲線。

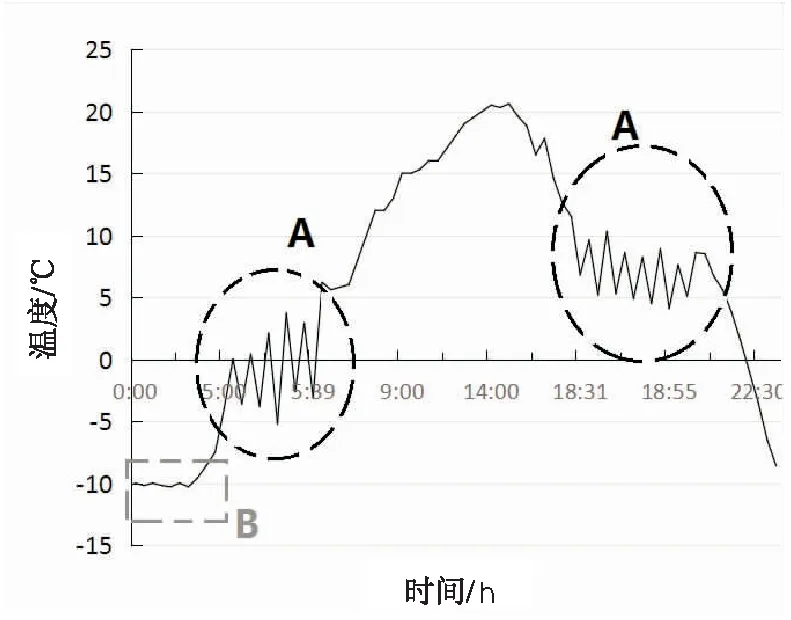
圖1 氣溫變化曲線

在臨近日出和日落兩個時間點，溫度的變化十分明顯，如A區域所示，但是在夜間的時候，整體的溫度變化幅度不大，如B區域所示。兩處的概率分布規律明顯不一致。如果用相同的概率分布基來表示兩處的概率分布，顯然不科學。因此，應該隨著時間的變化動態地更新用來表示概率分布的概率分布基，使其符合當前數據的變化趨勢。由此，引入了動態密度指標的概念。

動態密度指標[10]依托多種數學模型，可以從一條給定的時間序列中動態地推算出隨著時間變化的概率分布。然后，由這些動態密度指標推算得到的概率分布就可以用來創建概率數據庫，完成數據的存儲工作。已有的動態密度指標介紹如下。

1.2 已有動態密度指標

(1)統一閾值指標。

Cheng等[11]提出了一個通用的不確定數據的查詢估約框架。它的主要思想是將原始數據進行建模，將建模得到的數據范圍作為對應時間點數據的波動范圍。同時，該范圍也是該時間點所對應的真正值的所在范圍。然后在計算出的波動范圍中進行查詢操作，代替直接在原始值上進行查詢。

統一閾值指標(uniform thresholding metric，UT)的思想是上述思想的一種擴展，即通過推導得到對應時間點的一個“預期真實值”，然后以該“預期真實值”代表該時間點的原始真實數值，表示該點的概率分布。“預期真實值”的定義如下。

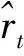
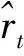
(1)

其中，(p,q)是非負整數，定義了模型的順序；φ1,φ2,…，φp是自回歸參數；θ1,θ2,…,θq是移動平均參數；φ0是一個常量；t>max(p,q)。

(2)可變閾值指標。

(2)

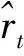
2 GARCH指標

由上述可知，統一閾值指標中u是一個固定值，這與實際情況不相符，因為在真實世界中，每個時間點的不確定范圍通常不是一個統一值，而是隨著時間的變化不斷發生改變。由圖1可以看出，區域A數據波動明顯，而區域B數據波動較為平緩。區域A和區域B數據的波動規律不一致，在進行數據的表示時不能使用統一的概率密度方程籠統代替。通過進一步研究發現，在進行一個概率密度函數推算時，底層的描述模型加入均值和時變方差能夠很好地提高數據描述的精度，由此提出了GARCH密度指標的概念。

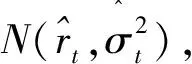
2.1 GARCH模型

(3)

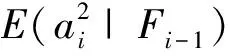
(4)

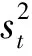
(5)

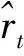
1．推算模型ARMA(p,q)，得到ai，其中t-H+max(p,q)≤i≤t-1

2．根據ai推算模型GARCH(1,1)

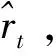
4．ub←rt+kσt,lb←rt-kσt

2.2 加強的GARCH模型I-GARCH

在實際中，時間序列通常存在噪聲點或者錯誤值，例如傳感器錯誤、網絡斷開等。上述提出的GARCH模型只適用于處理數據精確的不確定時間序列，對于包含錯誤數據的時間序列沒有很好的性能。為了解決這一問題，提出了一種加強的GARCH密度指標I-GARCH(improved GARCH)。

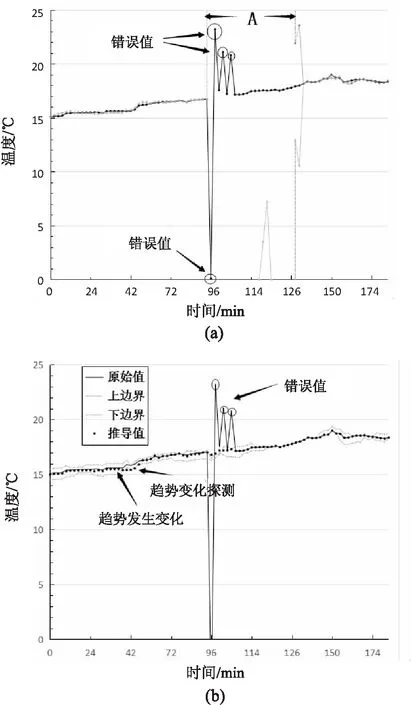
圖2 ARMA-GARCH和I-GARCH舉例說明

3 I-GARCH動態指標的改進

盡管在現實中，一條時間序列連續出現錯誤值的可能性很小，但是為了確保數據的精確性，提出了一種新的方法，用來過濾I-GARCH模型中的錯誤值，稱為錯誤值過濾算法EVF(erroneous value filtering)。

算法的輸入為包含錯誤值的時間序列V=[v1,v2,…，vk]以及閾值參數DTmax和Emax。具體的實現步驟如下：

(1)計算記錄了一條時間序列V中，兩兩相鄰的數據之間的差值；

(2)遍歷差值集合，根據DTmax判斷該差值是否在允許范圍內，如果小于閾值參數，默認該數值為正確值；如果差值大于閾值，則繼續遍歷；

(3)如果連續出現差值超過閾值的情況，記錄出現的次數，如果該次數大于Emax，則認為這些連續的點并非錯誤值，而是時間序列的走勢發生了明顯的變化，原始數值不作變動，繼續向下遍歷；

(4)反之，當記錄的次數在閾值范圍內，則說明該點為異常點。找到該點在序列中的位置，將其刪除。并通過線性插值的方法計算新的值代替原有錯誤值。

算法2：EVF

輸入：包含錯誤值的時間序列V，差值閾值DTmax，連續錯誤個數閾值Emax

輸出：干凈值序列V

李順過來說，六如叔，你怎么這么擰呢，社區開發那是鄉里開會訂下的，你那個合同也不頂事。再說，還是人家佟老板救了你，你總不能恩將仇報吧。

1．ArrayList differList=new ArrayList<>();

2．int differ=0;int count=0;

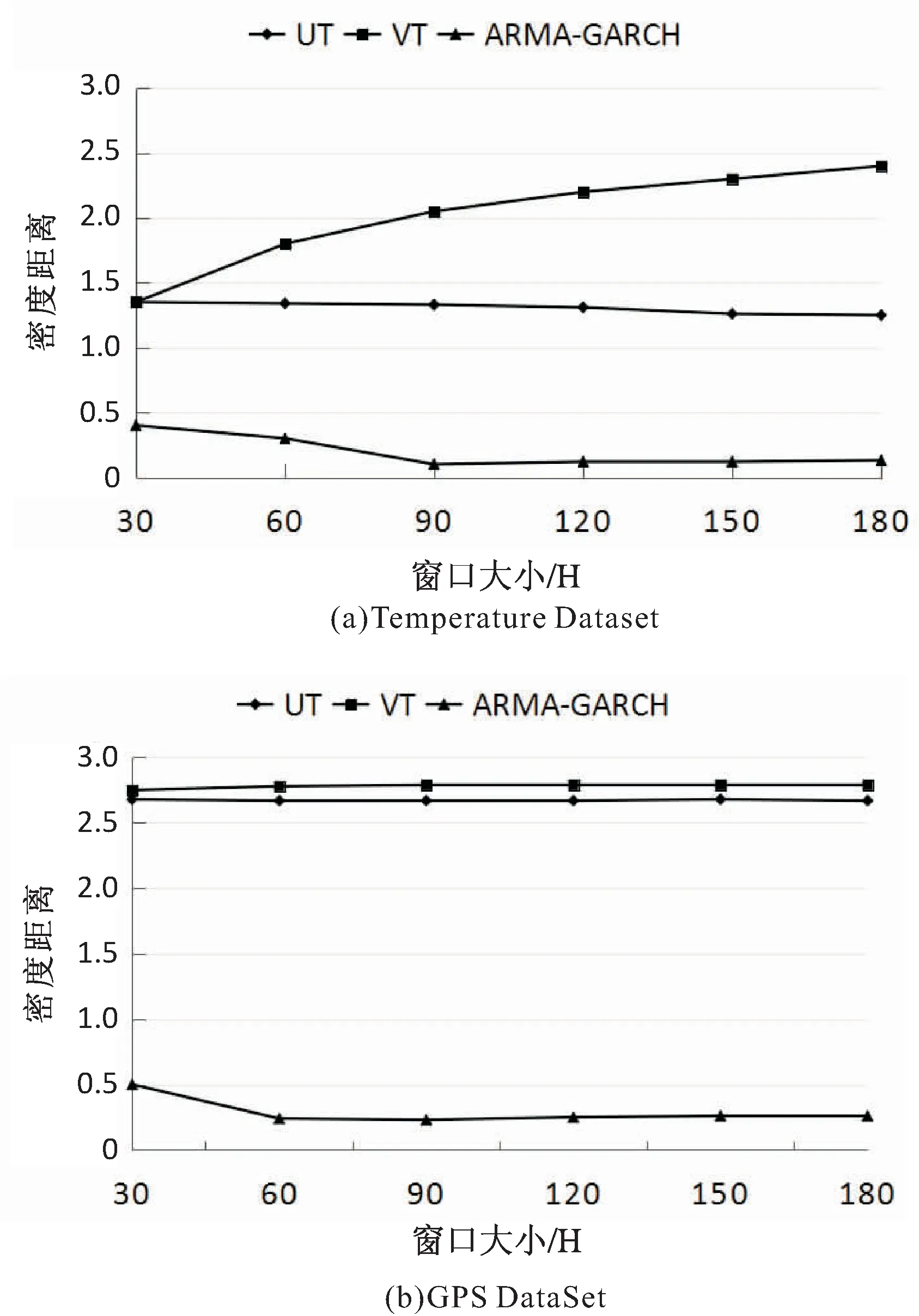
3．for(int i=1;i

4．differ=abs(vi-vi-1);

5．differList.add(differ);

6．}

7．ArrayList posList=new ArrayList<>();

9．while(i

10．int count=0;

11．while(differList.get(i)

12．while(differList.get(i)>DTmax&& i

13．if(count

14．}

15．for(int i=0;i

16．Vi+1為錯誤值將其刪除;

17．使用(vi+vi+2)/2線性插值代替Vi+1;

18．}

4 實 驗

4.1 實驗目的

實驗目的主要有兩個：驗證提出的動態密度指標ARMA-GARCH對于真實數據集有良好的準確性與高效性；比較ARMA-GARCH與I-GARCH，驗證添加了錯誤過濾的I-GARCH模型對處理包含錯誤數據的數據集的優越性。

4.2 實驗數據

實驗數據取自兩個真實的數據集。一個是Temperature Dataset，該數據集記錄了20天內傳感器網絡監測得到的氣溫變化的所有數據，約21 000條樣本數據。另一個數據集為GPS Dataset。這個數據集包括從導航系統記錄的192輛車的GPS日志。每一個日志元組包含時間和x-y數值，本實驗只取用其中的x數值。該數據集包含約10 000條數據。兩個數據集的詳細情況如表1所示。

表1 實驗數據說明

4.3 實驗方法

(1)動態密度指標的衡量。

設p1(R1),p2(R2),…，pt(Rt)是用動態密度指標推導得到的概率分布序列，z1，z2，…，zt為相應的概率積分變換值。則只有當pt(Rt)等于真正的密度分布pi(Ri)時，z1，z2，…，zt才會均勻分布在(0,1)之間。實驗使用直方圖近似法驗證z1，z2，…，zt的累計分布方程，判斷其是否為均勻分布，將其累計方程定義為Oz(z)，同時定義在(0,1)上均勻分布的標準累計方程為Uz(z)。定義Oz(z)和Uz(z)之間的差距為密度距離，表達式如下：

密度距離可以量化地測量觀察值分布，z1，z2，…，zt和它們的預期分布之間的差距，因此可以作為衡量動態密度指標的標準。

(2)實驗過程。

第一部分：動態密度指標的比較。

將提出的ARMA-GARCH與統一閾值和可變閾值進行比較。所有的評估都在兩個數據集上進行。使用密度距離作為衡量各個動態密度指標質量的標準。同時，也比較了各動態密度指標的運行效率，以運行時間作為衡量的標準。

第二部分：I-GARCH和ARMA-GARCH的比較，實驗在Temperature Dataset上進行驗證。為了比較兩個指標對于處理數據的精確性，在原有數據中插入人工合成的錯誤數值，即隨機地在原始數據中插入數值遠高于或低于正常范圍數據的數值。以捕獲錯誤值的數目和運行時間作為衡量兩個指標優劣的標準。

4.4 實驗結果與分析

(1)第一部分的實驗結果。

圖3 動態密度指標比較

圖3顯示了隨著窗口尺寸(H)的增大，各種動態密度指標在兩個數據集上的密度距離的比較。從圖中可以明顯看出，MARA-GARCH優于原始的動態密度指標。

圖4顯示了執行一次密度推算迭代所需的平均時間。由圖中可以看出，雖然ARMA-GARCH的執行時間總體上超出原始動態密度指標，但是差距并不明顯，大約在0.2～0.4 s左右。考慮到其在準確度和效率上的優勢，ARMA-GARCH仍是性能最好的動態密度指標。

圖4 動態密度指標效率比較

(2)第二部分的實驗結果。

圖5 I-GARCH和GARCH的比較

綜上，文中提出的ARMA-GARCH模型及I-GARCH模型與已有的統一閾值指標(UT)以及可變閾值指標(VT)相比具有很大的優勢，可以準確地推算出不確定時間序列的概率密度分布，在準確度和時間消耗上優勢明顯；同時，優化了I-GARCH指標，提出的算法EVF可以很好地檢測出不確定時間序列中的錯誤值，進行錯誤值的清洗與替換，具有良好的容錯性和一般通用性。

5 結束語

不確定時間序列的概率分布隨著時間的變化而不斷改變，無法使用已有的概率數據庫生成方法直接對其進行數據庫生成操作。因此在進行數據的存儲之前，需要對原始數據進行有效的概率分布推導工作，得到不確定時間序列數據隨著時間變化的一般分布規律。文中依托已有的ARMA模型和GARCH模型，提出推導不確定時間序列概率分布的ARMA-GARCH模型以及I-GARCH模型，并且在此基礎上進行進一步的改進，提出能有效過濾錯誤值的算法EVF。實驗結果表明，ARMA-GARCH模型和I-GARCH模型能有效地根據時間序列的發展規律推導得出正確的概率分布。同時，針對包含錯誤數據的數據集，EVF算法體現出高效的錯誤排查功能，具有良好的容錯性和一般通用性。下一步的研究工作是利用推導得出的概率分布生成不確定時間序列的概率數據庫。