配電變壓器豎板換熱特性的數值研究
鞠文杰
(華北電力大學,北京 102206)
1 引言
為維持配電變壓器的可靠運行,采用有效可靠的手段進行及時散熱是十分必要的[1]。矩形翅片由于其經濟性和可靠性而備受歡迎[2],經常被用來安裝在基板上實現散熱。與強迫對流相比,自然對流具有簡單、經濟、可靠性高、易維護、無噪聲等有優點,因而應用更為廣泛。經由翅片向外的散熱包括對流換熱和輻射散熱,由于翅片所用的材料發射率一般較低,輻射換熱對總的換熱量的影響相當小。由對流換熱的方程Q=hAΔT可知,,在ΔT一定時,要增大對流換熱量,可以通過提高h或A來實現。在一個固定的空間內增加翅片表面積固然可以增大對流換熱量,但如果翅片間距不合適,將會導致傳熱惡化,從而降低表面傳熱系數,進而影響對流換熱量。同理,對于不同的豎板高度其自然對流換熱量最大時的最優間距也理應不同。
2 研究模型
研究模型為兩豎板組成的二維模型,如圖1所示。豎板高度為H,豎板間距為W,H及W可變。兩豎板分別設為恒壁溫或恒熱流,下邊界為壓力入口,上邊界為壓力出口。由于自然對流的作用使得空氣從研究區域中流過并將豎板的熱量帶走。兩豎板的材質設為鋁,發射率很低,大約為0.1,故輻射換熱忽略不計。經計算發現所研究模型的Ra的數量級為107,空氣流動在層流區,故選用層流模型。除密度項采用Boussinesq假設外,其余物性參數為常數。對控制方程的求解采用非結構化網格的有限容積法進行離散,壓力與速度的耦合處理采用Simple算法。壓力項的離散格式選用PRESTO!。
穩態自然對流流動與換熱的控制方程可以寫作
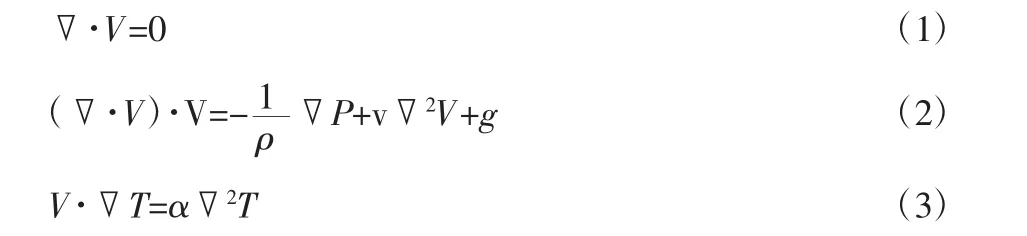
其中,V是速度矢量,g是重力加速度矢量,T為溫度,V和α分別是動量黏度及熱擴散系數,P為壓力,ρ為密度。
針對豎板間距為8mm,豎板高度為150mm選取4種網格尺寸進行網格無關性驗證。網格尺寸分別是1.5,1.2,1.0,0.5,對應的結構化網格數分別為500,875,3000,4800,以恒壁溫60℃下的自然對流換熱量作為評價指標,網格數為3000時換熱量比4800時的換熱量相比偏差不超過0.85%,故本文采用網格尺寸為1對模型進行網格劃分。
3 恒壁溫下豎板換熱特性研究
本文對恒壁溫 60℃下,豎板高度為 150mm、200mm、250mm、300mm,豎板間距為9~20mm,間隔1mm的結構組合進行了數值研究,獲得了豎板對流換熱量、豎板通道內最大流速及豎板通道內平均流速隨板間距及高寬比的變化規律。由兩豎板組成的通道,其換熱量隨豎板間距的增加而有所變化。為獲得可能的最優的高寬比(其中H為豎板高度,W為豎板間距),豎板間距隨著豎板高度的增加而增大。
不同高度豎板的換熱量均隨豎板間距的增加先增大后減小,存在最優豎板間距,使對流換熱量達到最大值。
不同高度的豎板,其表面傳熱系數均隨著板間距都是先增加至最大值然后減小,存在最優間距使表面傳熱系數最大。這與前面對流換熱量隨板間距的變化規律是一致的。在板間距相同時,豎板高度越高,其表面傳熱系數越小。
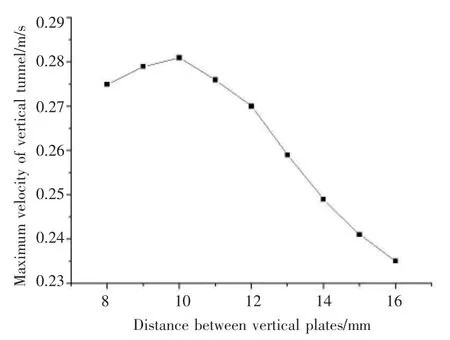
圖1 豎板150mm時通道內最高速度隨板間距的變化規律
圖1可知,豎板組成的通道內最高流速隨板間距的增加先增加至最大值然后減小。豎板高度為200mm、250mm、300mm時也得到了相同的結論,區別僅在于其最高速度對應的間距隨豎板高度的增加而變化。
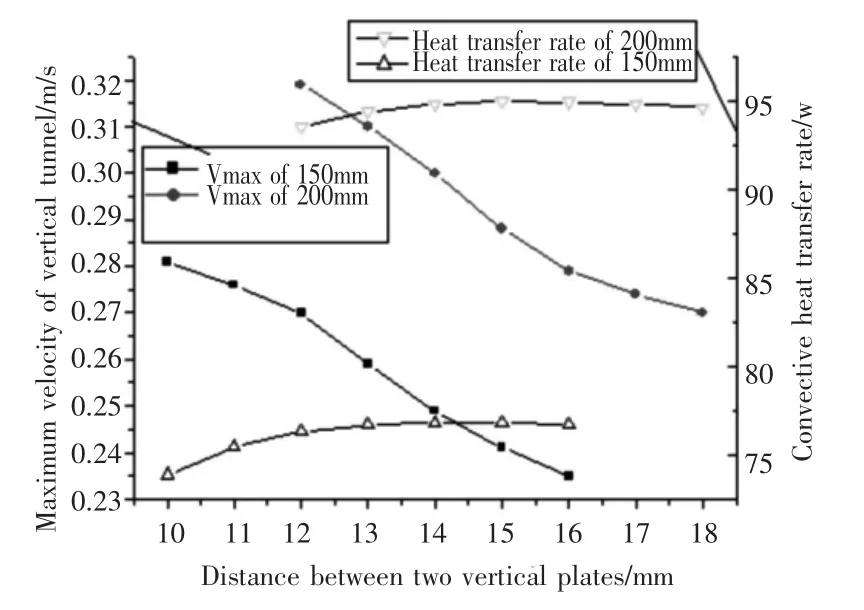
圖2 豎板高度為150mm和200mm時通道內流體的最大速度與換熱量的變化
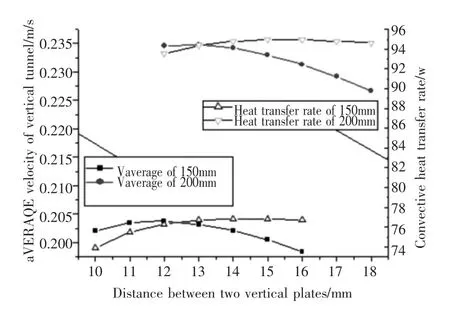
圖3 豎板高度為150mm和200mm時通道內流體的平均速度與換熱量隨間距的變化規律
圖2和圖3分別為豎板高度為150mm和200mm時通道內流體的最大速度與流體的平均流速與換熱量隨板間距的變化規律。圖4中可見,與豎板的對流換熱量隨間距的增加先增加后減小不同,豎通道內流體最大流速隨間距的增大而逐漸變小,兩者并不同步。這表明對流換熱量的變化與通道內的最大流速并不直接相關,還受到其他因素的影響。
圖3中可見,豎通道內流體平均流速隨間距的變化與豎板的對流換熱量隨間距的變化規律相似,都存在間距的最優值。只是換熱量最大相對應的最優間距(分別為14mm、15mm)與平均流速最高相對應的最優間距(12mm、13mm)并不重合,最大換熱量出現的間距值要高于最高平均流速出現的間距值。這表明分別以對流換熱量最大和通道內平均流速最大獲得的最優間距存在差異。
4 結論
本文對由配電變壓器內兩豎板組成的模型進行自然對流換熱特性的模擬,獲得的主要結論如下:
①不同高度豎板的換熱量均隨豎板間距的增加先增大后減小,存在最優豎板間距,使對流換熱量及表面換熱系數達到最大值。
②不同高度下豎板的換熱量隨高寬比的增加均是先增加后減小,存在最優高寬比,不同高度下其最優高寬比也不同。
③獲得了豎板溫度為60℃時豎板高度為150mm,200mm,250mm至300m最優板間距的預測關系式。

