肋骨不等間距布置對圓柱殼振動特性的影響

劉文璽，王路才，周其斗，李瀚欽，林鈺涵

(1. 海軍工程大學 艦船與海洋學院，湖北 武漢 430033；2. 海軍工程大學 兵器工程學院，湖北 武漢 430033；3. 海軍大連艦艇學院 航海系，遼寧 大連 116018)

0 引 言

隨著聲吶系統以及各種先進水下探測技術的發展，水下潛器的隱蔽性在現代戰爭中顯得極為重要。加肋圓柱殼結構是水下潛器的主要組成部分和結構形式，因此，研究它的振動及聲輻射特性非常重要，也一直得到眾多學者的關注。

在以往的圓柱殼研究中，研究的對象主要是環肋等間距布置的圓柱殼，也就是通常所說的周期性結構或等間距結構，對這類結構的振動特性的研究表明[1–3]，振動在頻域上有交替存在通帶與止帶的特征，其中，通帶代表結構波能自由傳播時的頻帶，止帶代表隨傳播距離的增大結構波幅值成指數衰減的頻帶。目前，對不等間距結構振動的研究多集中于一維簡單結構[4–10]，雖然得出了一些重要結論，如不等間距結構振動特性存在安德森定域效應現象，但針對不等間距加肋圓柱殼的振動特性的研究并不多，而且主要是針對無限長非周期加肋圓柱殼[11]，文獻[11]的研究表明，對于無限長非周期加肋圓柱殼，除低階周向振動模式外，不等間距加肋圓柱殼在軸向上的振動傳播均具有明顯的安德森定域效應，且安德森定域效應作用隨周向振動模式階數的升高而加強，主要原因是：隨著周向振動模式階數的升高，肋骨的阻抗作用變大，相鄰子結構間的耦合作用受肋骨阻抗影響而減弱。

在實際工程中，加肋圓柱殼有限長，本文研究肋骨不等間距布置對有限長加肋圓柱殼在一定頻率范圍內振動的抑制作用。

1 基本理論

1.1 一維不等間距結構振動理論

上世紀末至本世紀初，國外學者[5,7]對一維不規則耦合振子系統、一維不等間距支撐梁等簡單結構的振動特性進行研究，發現不等間距結構振動特性的主要特征是存在安德森定域效應（Aderson localization）。相比等間距結構上結構波在通帶內能無衰減地自由傳播，安德森定域效應描述了不等間距結構上的結構波幅值因為非阻尼的原因隨傳播距離增大成指數衰減的現象。

對一維無限長無阻尼單支座簡支支撐梁結構，若令支座處入射波為e?jkx，則透射波與反射波可分別表示為t?jkx與rejkx，其中t、r分別為結構波在單個支座處的透射與反射系數，k為結構波波數，見圖1（a）。

對一維無阻尼多跨度簡支支撐梁結構，由于結構波在各支座間存在來回的反射與透射，使得結構波的傳播較為復雜。假設僅考慮結構波的兩重反射，則在任意支座處，結構波的入射、透射、反射關系如圖1（b）所示。圖中，Xn為編號為n的簡支支座；xn為支座Xn與Xn+1的間距；入射波為 e?jkx，沿x軸正方向入射至支 座Xn；tn，Rn，R?n?1均為重整后的結構波透射與反射系數。

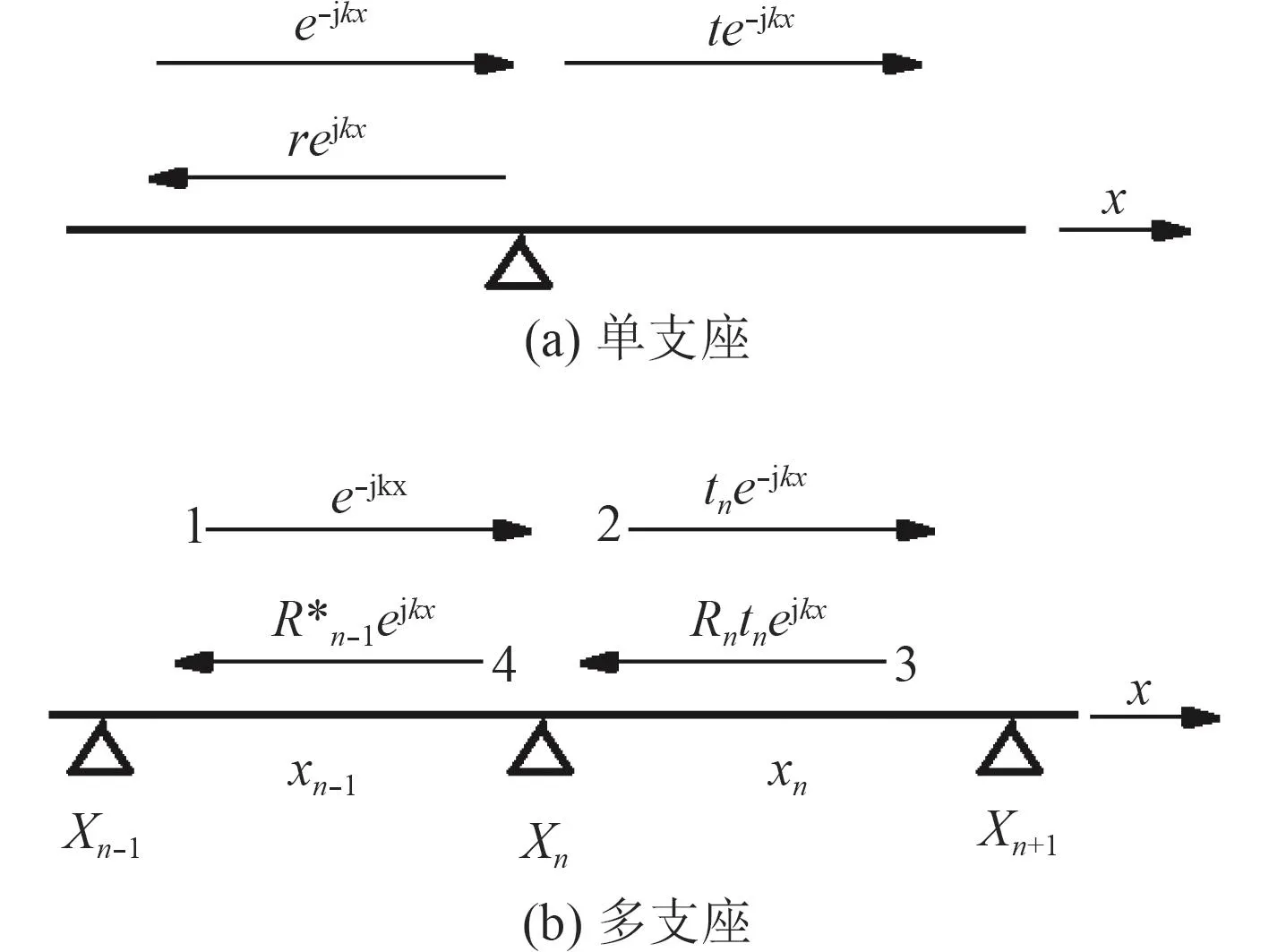
圖1 無限長單支座與多支座簡支支撐梁Fig.1 Infinite beam supported by single or multi simple supports

從圖1（b）可知，1標示為1的結構波為初始入射波。2標示為3的結構波為經支座 反射后，傳播至支座 右側的結構波。3標示為2的結構波由2部分疊加而成，一是結構波1在支座 處的透射部分，二是結構波3在支座 處的反射部分。至此，結構波已考慮了2次反射。4標示為4的結構波也由2部分疊加而成，一是結構波1在支座 處的反射部分，二是結構波3在支座 處的透射部分。根據上述結構波之間的相互關系，對多支座梁的結構波入射、透射、反射關系進行重整，得[5]：Xn+1Xn

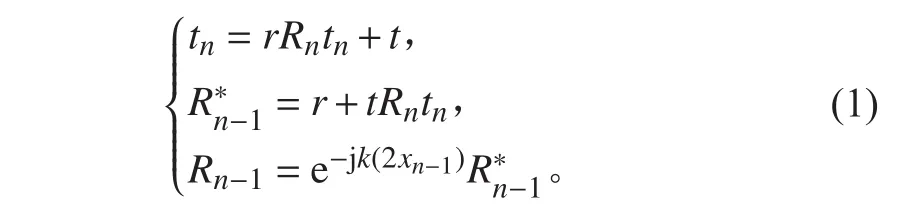
根據式（1）可得結構波在第n個支座處的透射系數：

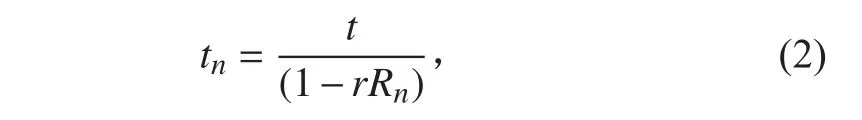
若結構波傳遞經過N個支座，則總傳遞系數T為：

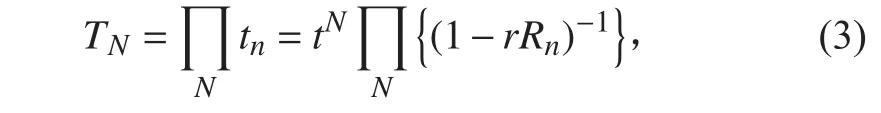
對總傳遞系數取對數可得：

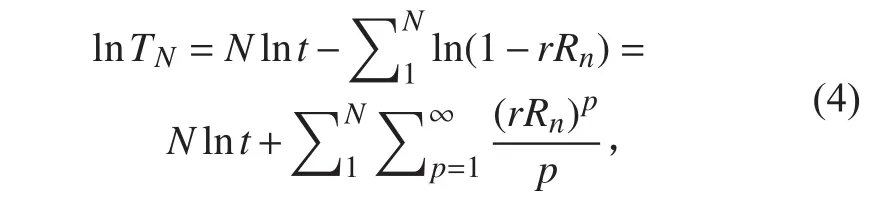
式中，由于|r|＜1|Rn|≤1 且 ，因此上式第2項是按泰勒級數展開后的結果。

若不等間距支撐梁的支座間距為隨機分布，則重整后反射系數間的相位因子也為隨機分布，因此式（4）可化為[5]：

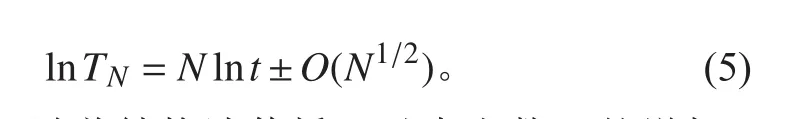
由上式可知，隨著結構波傳播經過支座數N的增加，總傳遞系數減小，結構波幅值隨傳播距離的增加成指數衰減，顯現了結構振動的安德森定域效應現象。

安德森定域效應的物理機理在于：結構的不等間距布置，破壞了結構傳播波在各支座位置處的相位匹配關系，使得支座對結構波的反射作用增強，傳播衰減增大。

1.2 肋骨間距設計方法

安德森定域效應以及文獻[11]結論，是從無限長結構、支座或者肋骨間距為隨機分布且數量較大得出的，而實際工程當中，加肋圓柱殼是有限長的，從工藝等角度看，肋骨間距隨機分布較難實現，所以，要尋找既能抑制圓柱殼振動，又能較容易實現的肋骨不等間距布置的方法。下面，把安德森定域效應的結論進行推廣，應用到有限長不等間距加肋圓柱殼，并通過數值計算進行檢驗，但問題的關鍵是肋骨間距的確定。

無論是無限長還是有限長的結構，肋骨間距的分布，應該滿足安德森定域效應產生的物理機理：結構的不等間距布置，要能破壞結構傳播波在各支座或肋骨處的相位匹配關系，使得支座或肋骨對結構波的反射作用增強，傳播衰減增大。根據文獻[11]，可以看出，安德森定域效應作用隨周向振動模式階數的升高而加強，也就是隨著固有頻率的提高，肋骨的阻抗作用變大，相鄰子結構間的耦合作用受肋骨阻抗影響而減弱，因此，本文從工程實用的角度出發，采取如下研究思路：

1）研究肋骨不等間距布置對有限長圓柱殼在中高頻段的振動特性的影響。

2）取2種肋距，交替排列，為了最大程度滿足安德森定域效應產生的條件，盡量增加相鄰子結構固有頻率差來減弱相鄰子結構的耦合作用，這一點，也可以將文獻[12]的研究結果進行推廣得到：文獻[12]通過不等間距分艙增加相鄰艙段的固有頻率差，從而控制圓柱殼結構振動響應的譜峰頻率和幅值，取得了一定效果，把不等間距分艙推廣到不等間距肋距，并且研究的頻率范圍由不等間距分艙的低頻段推廣到中高頻段，能夠達到減弱振動的目的。

2 肋骨間距設計

在2種情況下，一是只改變肋骨間距，二是只改變殼板厚度，研究兩端帶肋骨的圓環振動固有頻率的變化規律，為后面的加肋圓柱殼肋骨排列形式、殼板厚度分布設計奠定基礎。

2.1 肋骨間距對肋骨間圓環振動固有頻率的影響

2.1.1 計算模型

肋距均勻分布的加肋圓柱殼的結構形式如圖2所示，圓柱殼兩端用艙壁封堵，改變肋骨間距，外殼板厚度和肋骨尺寸不變，

計算模型的主要尺度如表1所示，各個模型肋骨間距不同。

2.1.2 計算結果

對于表1中的5個模型，以每個加肋圓柱殼中間相鄰2根肋骨間的圓環為對象，提取周向2個波形的圓環的固有頻率，振型如圖3所示。

固有頻率隨肋骨間距的變化曲線以及該曲線的擬合曲線如圖4所示，擬合曲線斜率的絕對值隨肋骨間距的變化曲線如圖5所示。

圖2 加肋圓柱殼的結構形式簡圖Fig.2 Diagram of structure form of ring-stiffened cylindrical shell

表1 各計算模型的主要尺度Tab.1 Main dimensions of models

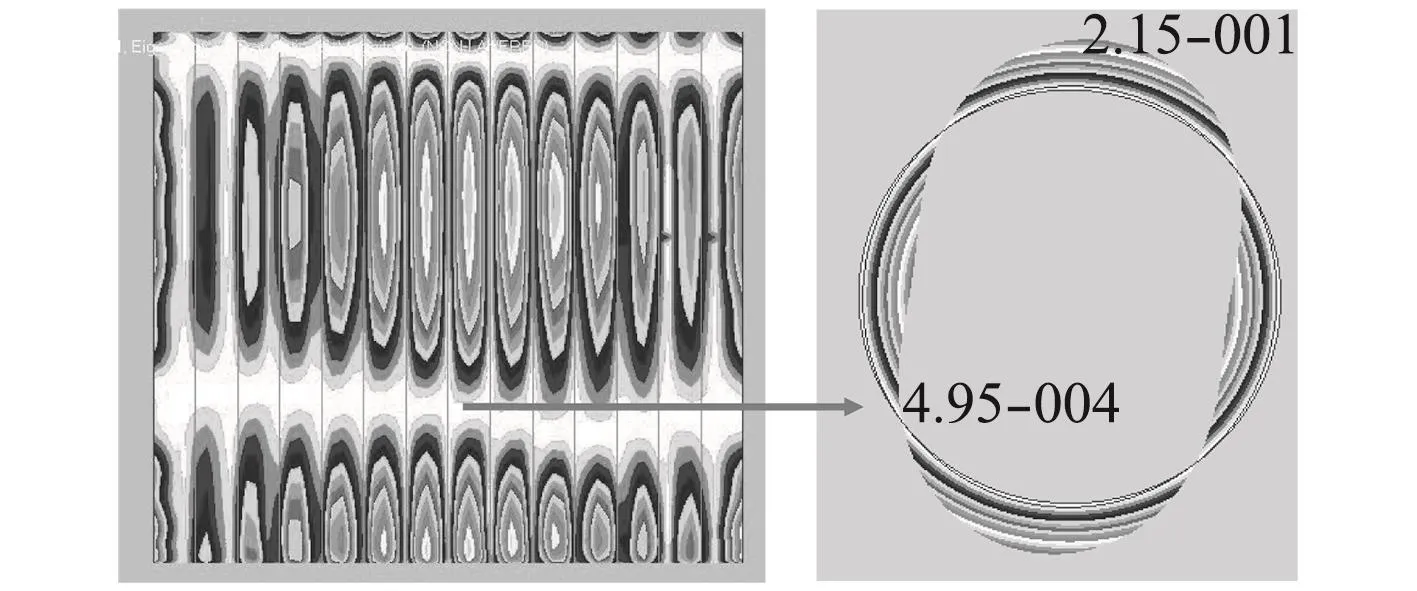
圖3 振型圖Fig.3 Vibration mode

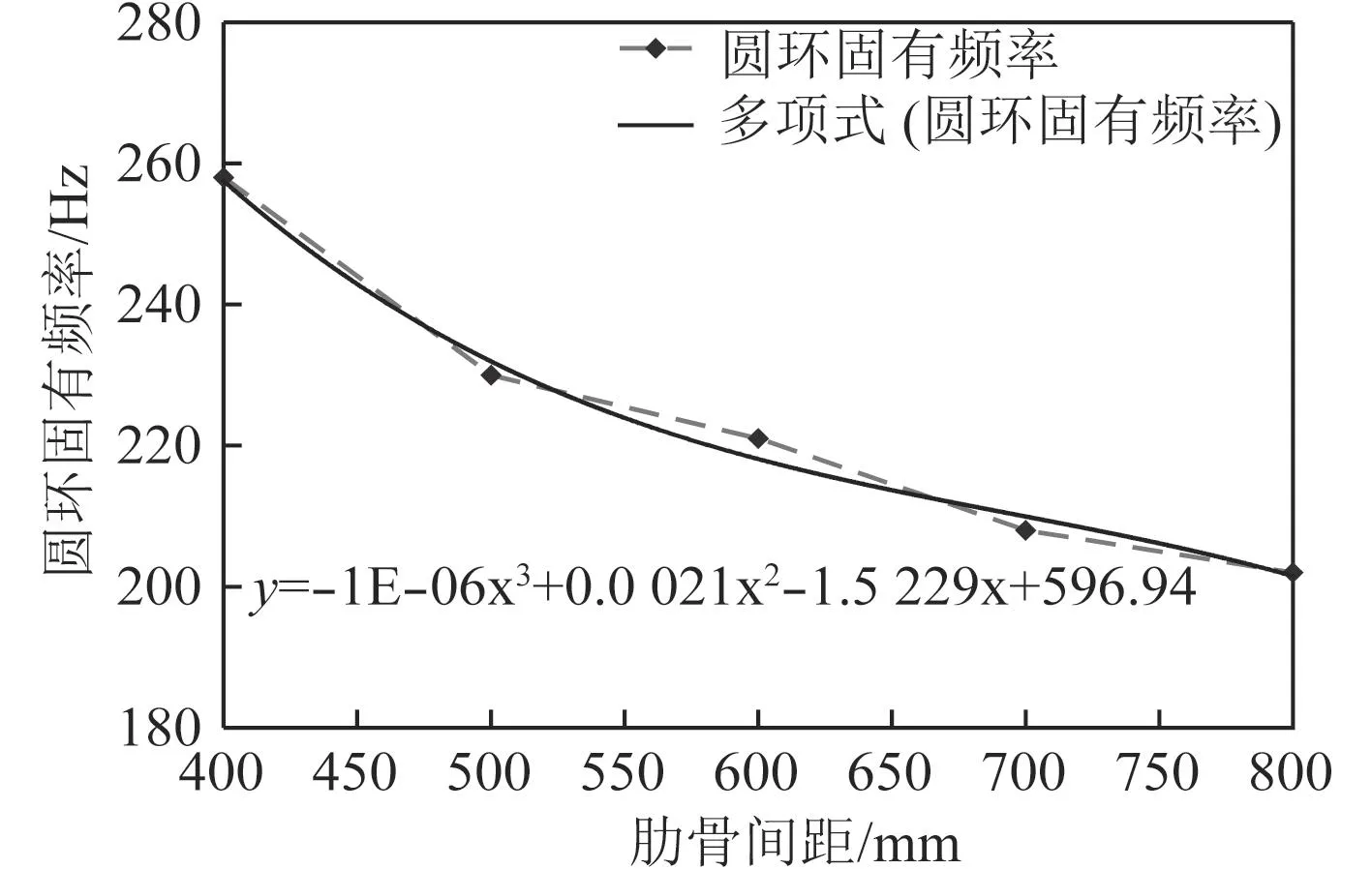
圖4 圓環固有頻率隨肋距的變化Fig.4 Variation of natural frequency of ring shell with frame spacing

根據擬合曲線斜率變化的情況，可以看出，肋距在600 mm之前，固有頻率變化較快，在600～800 mm之間，固有頻率變化較慢，因此，在選擇肋骨間距時，在滿足布置和工藝等要求的情況下，小間距的應盡量小，大間距的選擇700 mm左右就可以，因為再增大肋骨間距，對固有頻率變化的改變效果不大。

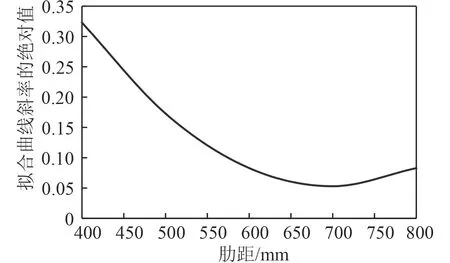
圖5 擬合曲線斜率的絕對值Fig.5 Absolute value of fitting curve slope

2.2 板厚對肋骨間圓環振動固有頻率的影響

2.2.1 計算模型

肋距均勻分布的加肋圓柱殼的結構形式如圖2所示，肋骨間距取3個值，分別是400 mm，600 mm，800 mm，對每個肋骨間距，圓柱殼板厚分別取28 mm，32 mm，36 mm，40 mm，44 mm，因此，構造了3組圓柱殼，每組5個，各圓柱殼肋骨尺寸不變，同2.1.1節模型，圓柱殼兩端用艙壁封堵。

2.2.2 計算結果

以每個加肋圓柱殼中間相鄰2根肋骨間的圓環為對象，提取周向2個波形圓環的固有頻率，結果如圖6所示。

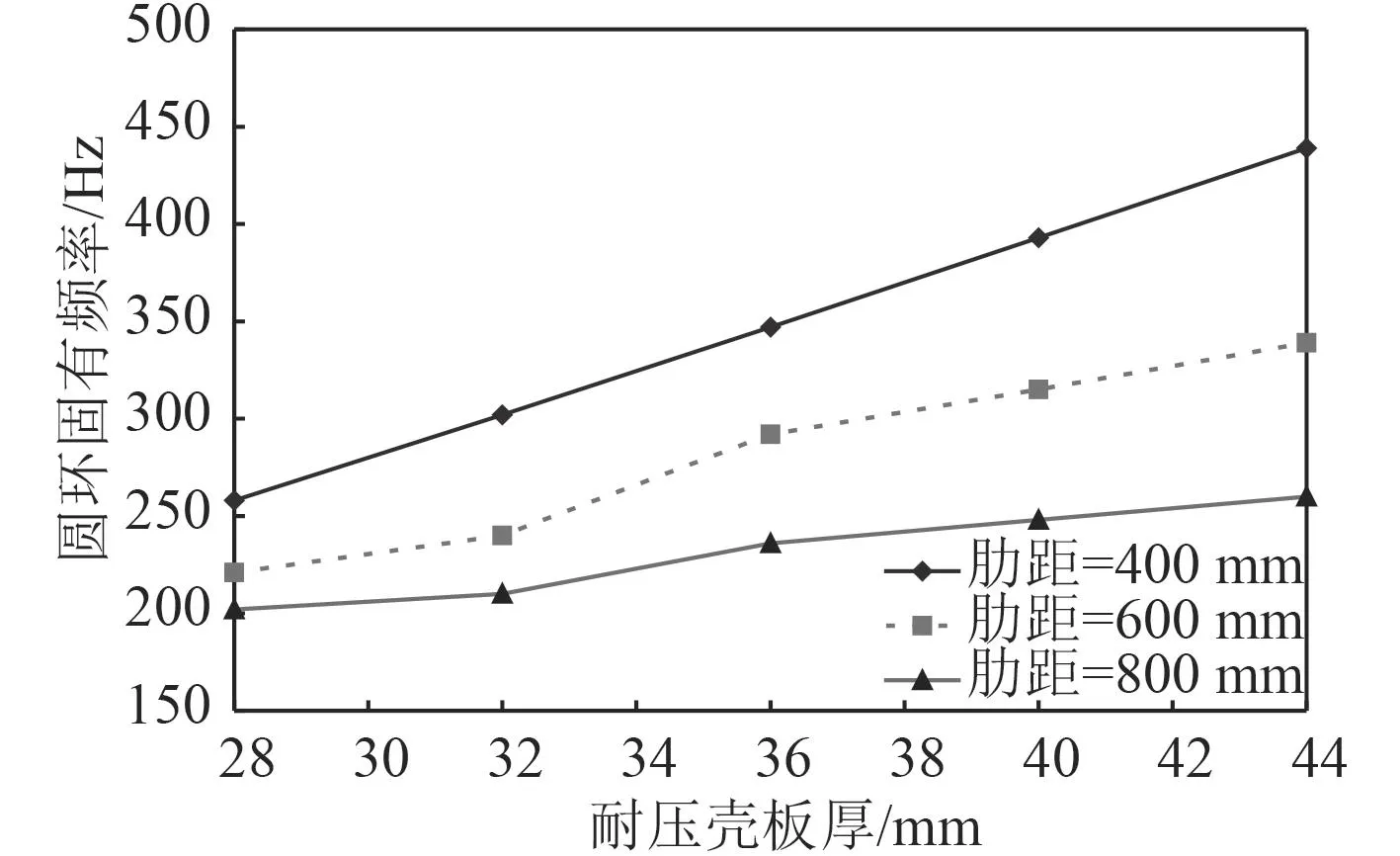
圖6 圓環固有頻率隨殼板板厚的變化Fig.6 Variation of natural frequency of ring shell with shell plate thickness

根據圖6的結果，可以看出：

1）圓環固有頻率隨著圓柱殼板厚的增加而增大；

2）肋骨間距小，固有頻率增大的速度快，肋骨間距大，固有頻率增大的速度慢；

3）隨著圓柱殼板厚的增加，肋距600 mm與肋距400 mm，800 mm相比，固有頻率差別都較大，因此，當肋距選擇800 mm時，為了與肋距600 mm時的固有頻率差盡量大，板厚應大于36 mm。

3 加肋圓柱殼振動響應對比研究

3.1 加肋圓柱殼結構設計

1）等間距加肋圓柱殼結構設計

肋骨間距600 mm，圓柱殼板厚28 mm，圓柱殼長度8 400 mm，兩端的艙壁不變，圓柱殼的結構形式如圖7（a）所示。

2）不等間距加肋圓柱殼結構設計

根據2.1.2節和2.2.2節的結論，選擇2種肋骨間距，分別是400 mm，800 mm，肋距400 mm之間圓柱殼板厚28 mm，肋距800 mm之間圓柱殼板厚分別選28 mm，32 mm，36 mm，40 mm，44 mm，因此，一共構造了5個不等間距加肋圓柱殼，即5個計算模型，圓柱殼長度都是8 400 mm，兩端的艙壁不變，圓柱殼的結構形式如圖7（b）所示。

圖7 加肋圓柱殼結構設計Fig.7 Structure design of ring-stiffened cylindrical shell

3.2 加肋圓柱殼在空氣中的振動響應

分別計算等間距和不等間距加肋圓柱殼在空氣中的振動響應，計算工況有2個，分別是艙壁浮筏基座處軸向激振、垂向激振，激振力的頻率范圍20～1 000 Hz，對比分析各模型的均方振速，均方振速的計算公式參見文獻[12]。可以看出，等間距加肋圓柱殼和不等間距加肋圓柱殼中的肋距800 mm之間圓柱殼板厚44 mm的模型的振動響應差別最為明顯，如圖8和圖9所示。圖8表示軸向激振的結果，圖9表示垂向激振的結果。

根據圖8和圖9的結果，可以看出：

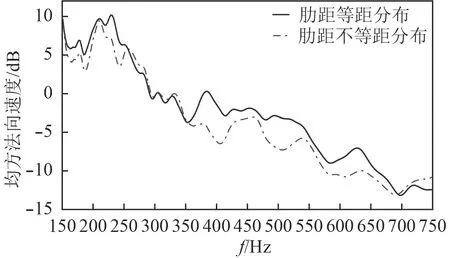
圖8 軸向激振力作用下圓柱殼均方振速級比較Fig.8 Comparison of level of mean square speed of cylindrical shell under axial loads

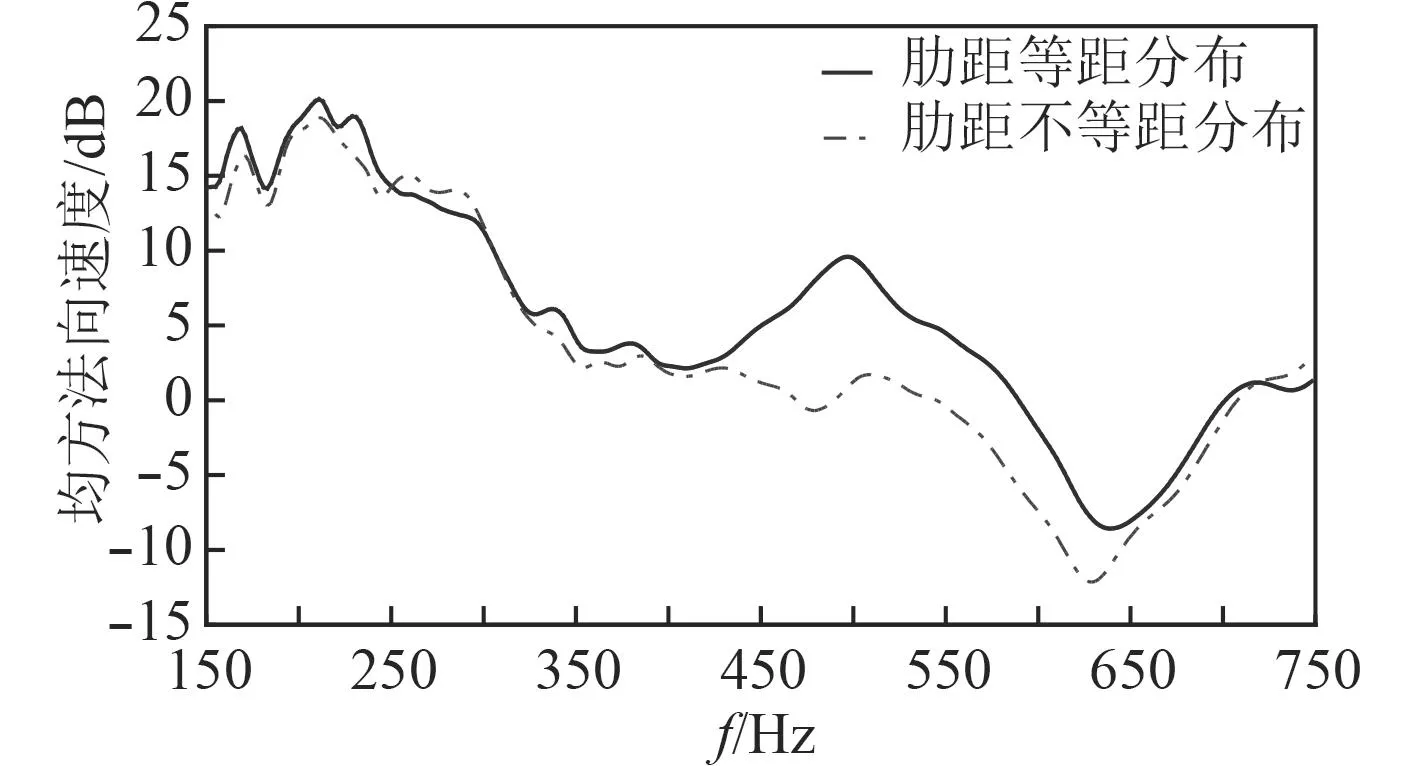
圖9 垂向激振力作用下圓柱殼均方振速級比較Fig.9 Comparison of level of mean square speed of cylindrical shell under vertical loads

1）對于有限長加肋圓柱殼，當激振力的激振頻率小于350 Hz時，肋骨采用等間距排列形式和不等間距排列形式，振動響應相差不大其原因是：低頻時結構波長較長，肋骨排列形式對殼體總振動影響較小，隨著頻率增高，結構波長變短，肋骨排列形式對殼體振動的影響才體現出來；當激振力的激振頻率大于350 Hz而小于700 Hz時，肋骨采用不等間距排列形式，相對于肋骨采用等間距排列形式，可以減弱結構振動。

2）對于有限長圓柱殼，肋距不等間距分布，可以達到降低圓柱殼振動的目的，但是，只是在較窄的一定的頻率（一般是中高頻率）范圍內。

4 結 語

本文對不等間距加肋圓柱殼的振動特性進行研究。將安德森定域效應的原理進行推廣，按照盡量增加相鄰子結構固有頻率差來減弱相鄰子結構的耦合作用的思路，設計了不等間距加肋圓柱殼肋骨間距的分布形式，計算并比較了加肋圓柱殼的振動響應，可以看出：

1）肋骨排列形式對圓柱殼振動的影響主要體現在結構波波長小于肋間距的中高頻，低頻時影響不大；

2）在一定頻率（一般是中高頻率）范圍內，采取不等間距肋距分布形式可以減弱加肋圓柱殼的振動響應；

3）采用盡量增加相鄰子結構固有頻率差的思路確定有限長圓柱殼肋骨間距可行；

4）在以后的研究中，可以基于此基礎上進行進一步的研究。