圓柱殼水下振動的截斷模態規律性研究

仝 博，李永清，朱 錫，張焱冰

(海軍工程大學 艦船工程系，湖北 武漢 430033)

0 引 言

圓柱殼結構是船舶領域被廣泛應用的一種工程結構形式，許多研究者對其水下振動已做了大量研究。線性范圍內，圓柱殼在外力作用下的振動響應可看作是其振動模態的疊加[1]，大多數值方法均是基于這一思想，比如瑞利-里茲法[2]、傳遞矩陣法[3]、基于模態疊加的有限元法等。數值計算追求最小的計算成本達到較高的計算精度。在運用模態疊加法研究結構振動響應時，模態階數的選取決定計算的經濟性和準確性。選取的模態階數越高，計算結果越準確，但消耗的計算時長卻越高。當模態數量大于一定值時計算結果變化不大，趨于穩定，把該值定義為截斷模態數。對截

斷模態數的研究通常是在理論方法基礎上對數值計算的相關參數的研究。比如王宇等[4]采用Love殼體理論分析了薄壁短圓柱殼在3種邊界條件下的振動位移響應，指出截取前八階模態就可達到相當精度。王獻忠等[5]結合精細積分法和傳遞矩陣法，提出精細傳遞矩陣法法，在對方法有效性驗證的同時開展了模態收斂性分析。李榆銀等[6]基于NASTRAN軟件對薄壁圓柱殼進行強迫振動分析時對截斷模態數進行了靈敏度研究，得到了有效的截斷波數。

也有學者專門研究了結構的模態截斷對結果的影響。李興泉等[7]基于有限元法對頻率截斷和有效模態質量截斷這2種截斷方法進行對比研究。張淼等[8]針對重頻阻尼系統提出了高精度截模態算法，并對該算法進行了模態靈敏度和誤差分析。金國光等[9]對高速凸輪結構進行動力學分析的同時進行了模態截斷研究，基于有限元法研究了不同截取階數對計算精度和計算速度的影響。也有學者未采用截斷模態數確定結構濕表面有限元網格尺度，而是以主模態分量波長作為參考尺度確定的網格尺度劃分原則[10]。但對于寬頻的振動響應計算，主模態變化較大，仍要以最高頻率確定網格尺度。以上對截斷模態的研究評判標準大多為單個節點的位移響應或聲壓響應，不具有代表性，且研究對象為單一圓柱殼，不具有普適性。

本文基于瑞利-里茲法求解圓柱殼振動方程，研究了35個不同尺度的圓柱殼在環頻率以下的水下振動響應，研究分析了截斷模態數隨長徑比和環頻率的變化關系，并且對其規律性進行總結，通過有限元仿真驗證了其正確性，結論對于圓柱殼水下振動問題的研究具有重要的參考意義。

1 圓柱殼水下振動方程推導

研究對象為水下有限長薄壁圓柱殼，長度為L，半徑R，厚度為h，h/R≤0.01，材料密度為 ρs，泊松比為μ，模量為E(1+η)， η為損耗因子，本文取0.01。殼體完全浸沒于水中，兩端簡支在無限長剛性圓柱障板上，如圖1所示。本文基于Donnell殼體理論研究圓柱殼徑向激勵下的振動問題，其運動方程為：

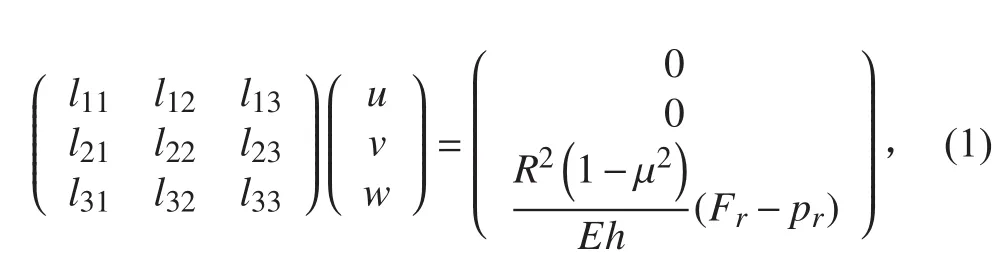
其中：位移系數矩陣各項表達式具體形式可查詢文獻[12]；u，v，w分別為軸向，環向和徑向位移；Fr為徑向載荷力，作用點位于殼體中部；pr為流體載荷。

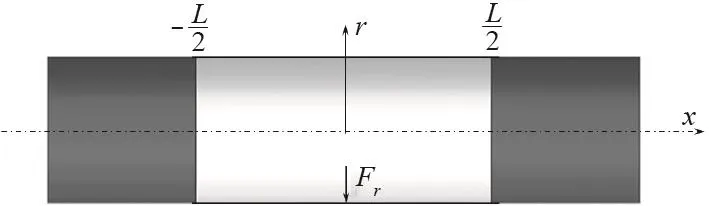
圖1 有限長圓柱殼模型Fig.1 Finite cylindrical shell model

為了分離圓柱殼的軸向和環向振型，采用分離變量法對軸向和環向位移進行分解，且基于里茲法的思想，位移可假定為一系列模態振型的線性疊加，其公式如下（忽略時間項eiωt）：

其中：m，n分別為軸向模態半波數和環向模態波數，km與邊界條件有關，對于本文的對稱激勵情況，圓柱殼的振動響應僅僅是對稱模態的疊加，即軸向半波數m為奇數的情況，因此將k取為 (2m+1)，m=0，1，m2……。

由模態展開法可對激勵力和圓柱殼周圍的流體載荷進行分解：

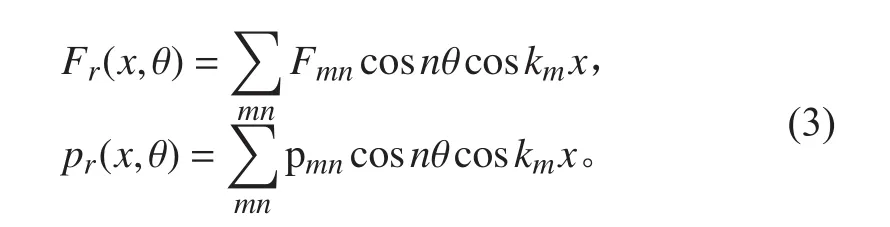
將式（2）和式（3）代入式（1）中，可得

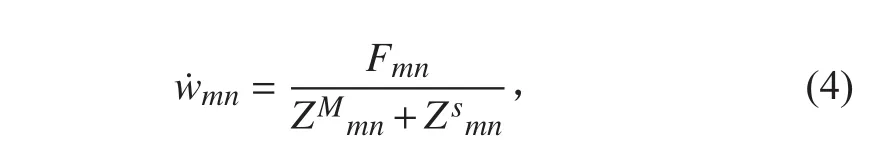
式中， 為機械阻抗，表達式為

ZMmn

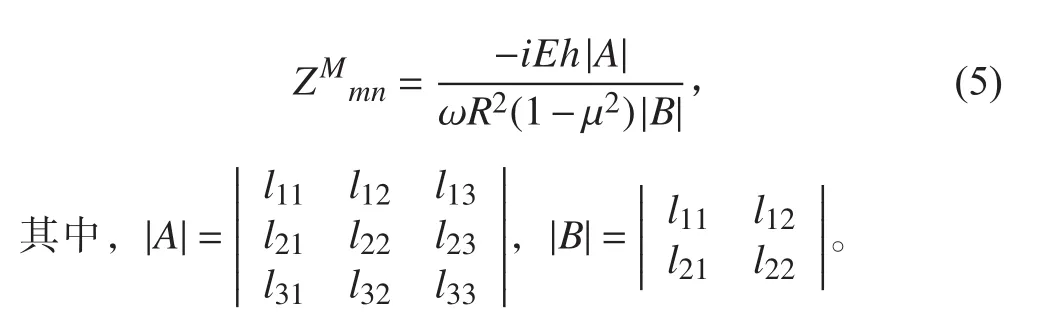
求解表面振速，還需要事先求得聲輻射阻抗，求解聲輻射阻抗的方法主要有流固耦合方法和聲固耦合法[13]2種。本文基于聲固耦合法計算Helmholtz方程[14]求解圓柱殼表面聲壓載荷，表達式為：

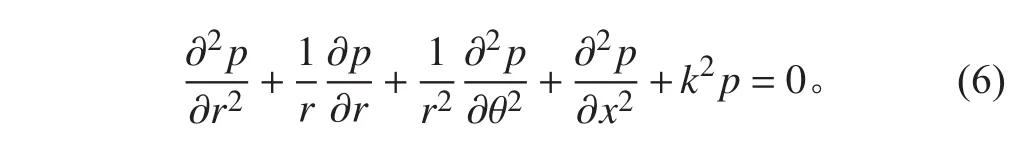
將式（3）代入上述方程，依據貝塞爾方程形式求解得聲輻射阻抗為：

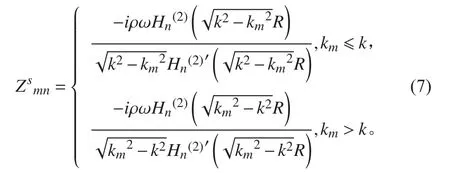
此時將式（5）和式（7）代入式（4）便可求得圓柱殼表面振速表達式。

圓柱殼表面均方振速公式為：

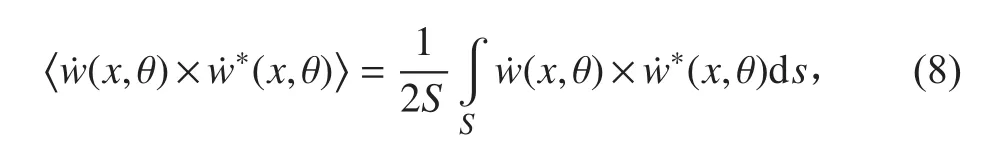
其中：

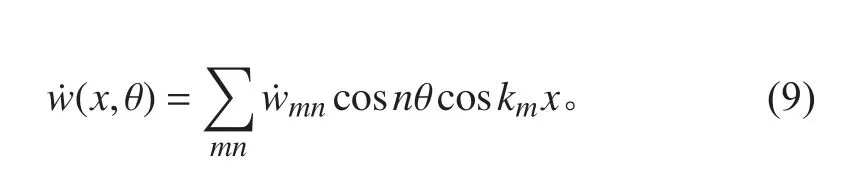
將式（9）代入式（8），依據余弦函數的正交性推導可得均方振速為：

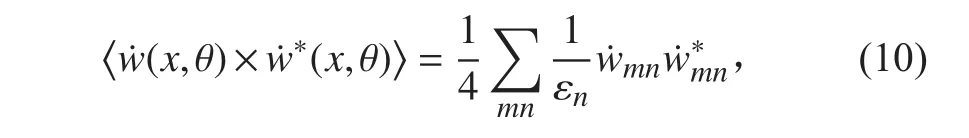
表面均方振速級公式：

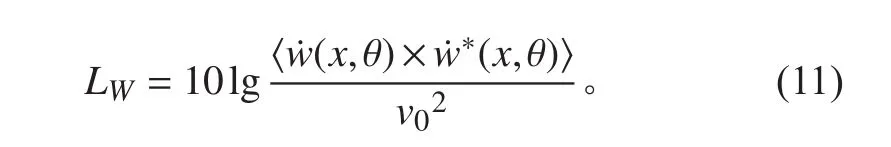
2 圓柱殼的模態截斷

在基于模態疊加法對圓柱殼進行水下振動特性問題研究時發現，不同尺度的圓柱殼，其截斷模態數量不同。因此針對不同尺寸的圓柱殼，根據上述圓柱殼振動理論方程，基于Mathematica軟件進行編程計算，得到圓柱殼表面均方振速。以表面均方振速級為評判標準，進行軸向半波數m和環向波數n的無關性研究。

2.1 圓柱殼模型

本文以35個不同尺度的圓柱殼為對象，計算它們在環頻率以下的水下振動響應，研究軸向截斷模態數m、環向截斷模態數n隨長徑比L/R和環頻率fr的變化關系。圓柱殼模型參數見表1。其中，環頻率公式為：

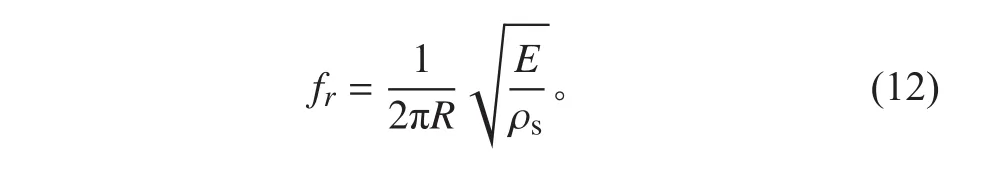
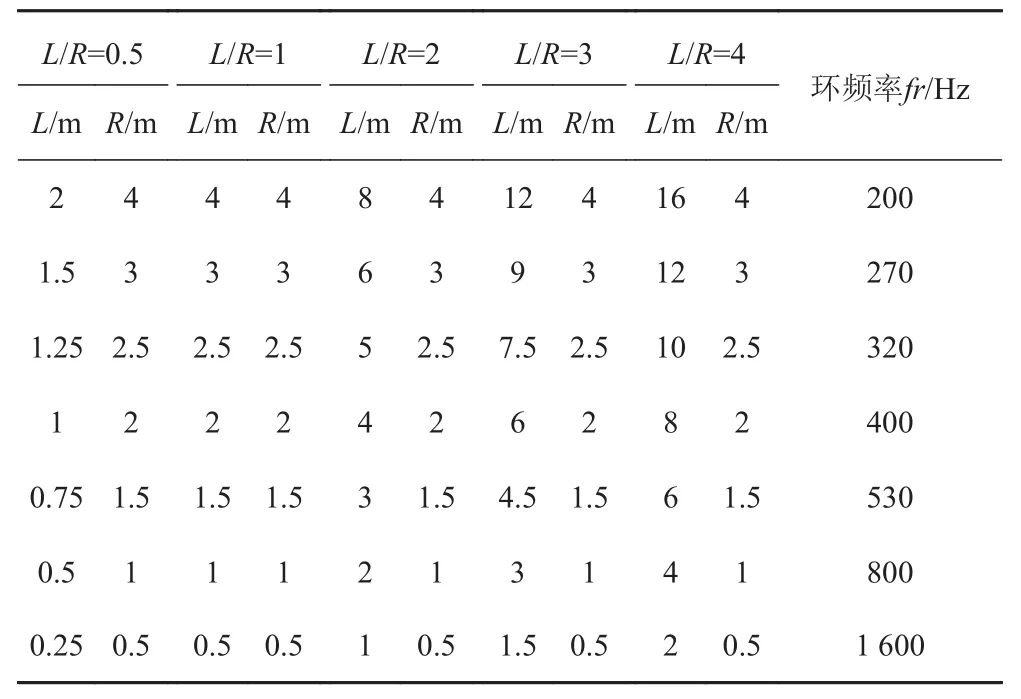
表1 圓柱殼參數Tab.1 Geometric parameters of cylindrical shells

2.2 截斷模態研究

在結構的動態力學特性計算中，為提高計算效率，在不影響計算精度的情況下，往往選取有限個模態數目作為主模態截斷，進而通過模態疊加得到結構表面的振動響應。本文目標是研究不同尺度的圓柱殼截斷模態數的選取規律，由于計算樣本較多，為提高計算效率，將環頻率以下的1/3倍頻程中心頻率作為計算頻率點，1/3倍頻程中心頻率計算式為：

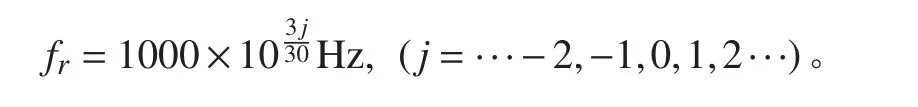
以均方振速級為精度判斷指標，具體要求是在環頻率以下，模態截斷時的計算結果與準確解誤差小于1%。理論上，m和n取無窮大時可得到準確解，但在實際計算中難以實現，因此可取一個相對較大的值進行計算作為準確解。以L=1 m，R=1 m圓柱殼為例，經計算分析，當軸向和環向截斷模態數達到100時，就能得到準確解。圖2和圖3分別反映了該圓柱殼軸向和環向截斷模態數取不同值時均方振速曲線對比。圖中可看出，隨著截斷模態數的增加，均方振速級曲線與準確解的吻合頻率區間不斷擴大，當軸向截斷模態數m達到8時，當環向截斷模態數n達到56時，就與m=n=100時的均方振速級曲線完全吻合，最大誤差低于1%，因此可將m=8，n=56作為該圓柱殼的截斷模態數。

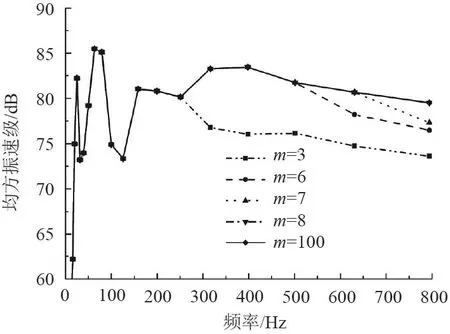
圖2 不同軸向截斷模態數時均方振速曲線對比（L=R=1 m）Fig.2 Comparison of mean square vibration velocity curves at different axial truncated modes (L=R=1 m)

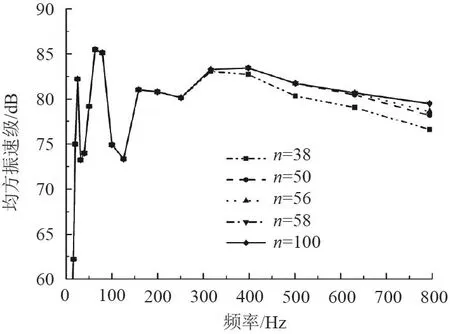
圖3 不同軸向截斷模態數時均方振速曲線對比（L=R=1 m）Fig.3 Comparison of mean square vibration velocity curves at different circumferential truncated modes (L=R=1 m)

對于表1中每個尺寸的圓柱殼都采用上述方法選取截斷模態，進行大量計算后將結果進行整理分析，其中專門研究了截斷模態數隨環頻率的變化關系，如圖4和圖5所示。圖中可看出，長徑比相同的情況下，隨著環頻率的增大，軸向和環向截斷模態數均呈下降趨勢，且下降趨勢逐漸平緩。對于軸向截斷模態m，長徑比越大，截斷模態數越高；但對于環向截斷模態n，不同長徑比圓柱殼其截斷模態數隨環頻率變化曲線趨于重合，說明環向截斷模態數對長徑比變化不敏感，它僅與環頻率有關，也就是與圓柱殼的半徑相關。

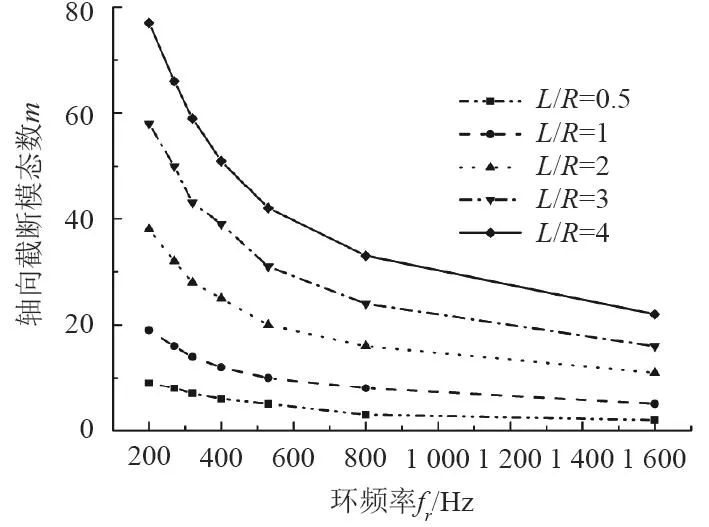
圖4 不同長徑比時圓柱殼軸向截斷模態數m隨環頻率變化趨勢對比Fig.4 Change trend of the axial truncated modal number with the ring frequency at different ratios of length to diameter

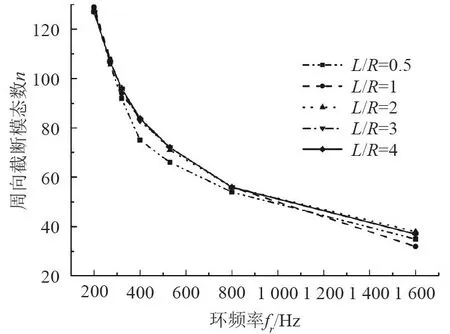
圖5 不同長徑比圓柱殼環向截斷模態數n隨環頻率變化趨勢對比Fig.5 Change trend of the circumferential truncated modal number with the ring frequency at different ratios of length to diameter

為研究圓柱殼振動截斷模態在軸向和環向的相對關系，建立關系式研究 ζ與環頻率的關系。簡單推導可得： ，即 ζ代表了軸向波長和r環向波長的比值。圖6反映了不同尺度的圓柱殼軸向和環向截斷模態波長之比。由圖可知，每個圓柱殼截斷模態對應的軸向波長與環向波長之比大體相同，均在2～2.5之間，平均值為2.14，即在保證圓柱殼環頻率以下的表面均方振速級最大誤差不超過1%的情況下，截斷模態滿足軸向波長大約為環向的2倍。

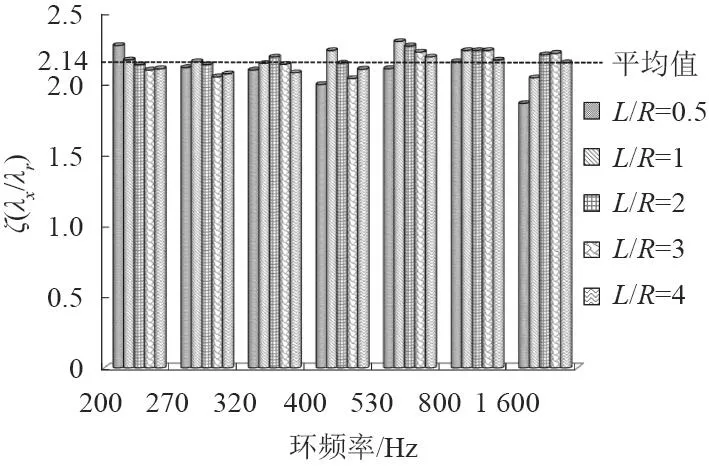
圖6 軸向和環向截斷模態波長比值Fig.6 Wavelength ratios of axial and circumferential truncated modes

3 有限元仿真對比分析

上述對截斷模態的研究是基于瑞利-里茲法求解圓柱殼振動方程，為驗證理論模型的可靠性和截斷模態選取規律的正確性，基于有限元方法進行圓柱殼水下振動特性計算，與理論算法進行對比。

算例對象：圓柱殼材料為鋁，長L為2 m，半徑R為0.8 m，厚度為2 mm，則長徑比L/R為2.5，環頻率為1 000 Hz。有限元計算采用結構有限元和流體有限元相結合的方法，基于直接穩態動力學法，對模型的原始方程直接積分計算。其中，圓柱殼周圍流場域截斷方案已在文獻[15]進行了探討，此處直接取柱形流場域半徑為5R，如圖7所示。

與理論模型不同的是，采用流體有限元法計算圓柱殼水下振動，殼體兩端必須進行封閉處理，為了消除兩端面對殼體振動的影響，端面除了邊緣一圈節點簡支，其余所有節點進行固支約束，如圖8所示。

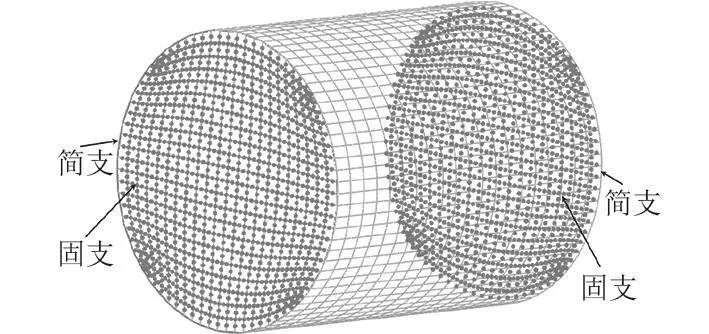
圖8 圓柱殼表面網格及邊界條件Fig.8 Surface meshes and boundary conditions of cylindrical shells

首先基于Mathematica軟件編程計算圓柱殼水下振動固有頻率，并與有限元仿真結果進行對比。結果如表2所示。表中可看出，低階模態計算誤差相比高階模態低，但最大誤差在6%左右，一致性較好。驗證了理論算法和有限元仿真的準確性。

其次基于Mathematica軟件編程計算圓柱殼水下振動響應，依據圖4和圖5插值可得截斷模態數m取20，n取50。求取環頻率以下的表面均方振速級，與有限元仿真結果進行對比，結果如圖9所示。由圖可知，在環頻率以下，理論方法和有限元仿真計算求得的均方振速曲線吻合較好，驗證了截斷模態選取的正確性。

4 結 語

本文基于瑞利-里茲法求解圓柱殼振動方程，研究了35個不同尺度的圓柱殼在環頻率以下的水下振動響應，以表面均方振速為評判標準，研究分析了軸向截斷模態數m、環向截斷模態數n隨長徑比和環頻率的變化關系，得到了同等精度下的截斷模態數，并且對其規律性進行總結，得出以下結論：

1）對于軸向截斷模態m，其大小與長徑比和環頻率均相關。長徑比相同，隨著環頻率的增大，截斷模態m逐漸降低，且下降趨勢逐漸平緩；環頻率相同，長徑比越大，截斷模態m值越高。

2）對于環向截斷模態n，其大小僅與環頻率相關。隨著環頻率的增大，n值逐漸減小。

3）在保證圓柱殼環頻率以下的表面均方振速級最大誤差不超過1%的情況下，截斷模態對應的軸向波長與環向波長之比大概滿足2倍的關系。

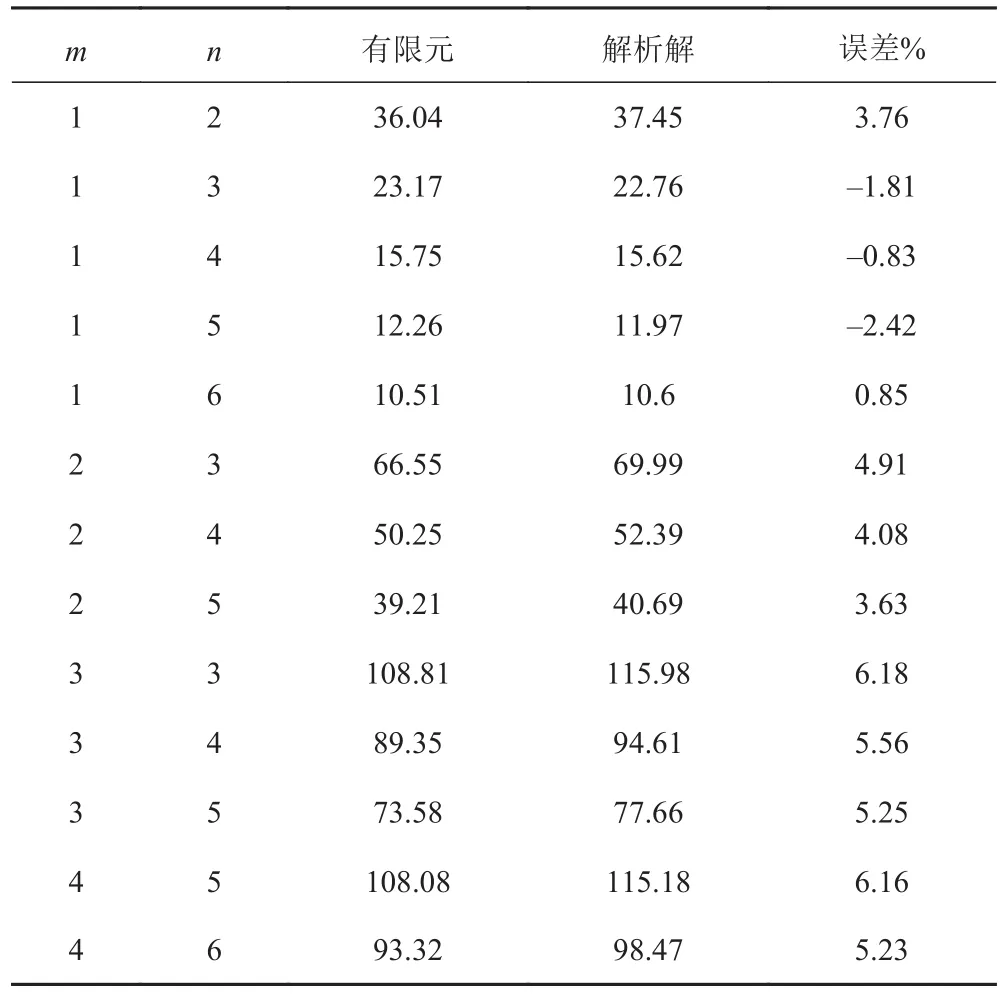
表2 圓柱殼固有頻率對比Tab.2 Comparison of natural frequencies of cylindrical shell

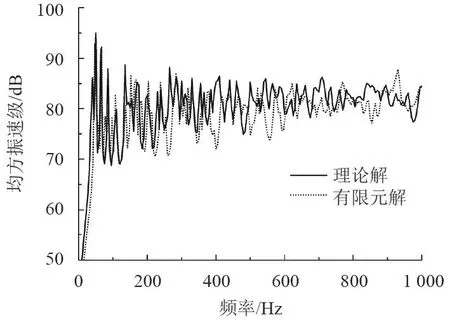
圖9 有限元法和理論方法計算均方振速對比Fig.9 Comparison of the mean quadratic velocity calculated by the finite element method and the theoretical method

4）采用理論方法和有限元法計算了圓柱殼的固有頻率和均方振速，通過對比，驗證了理論計算的正確性和截斷模態選取的合理性。