基于數值計算的水潤滑賽龍軸承仿真研究

王 昊，周新聰，王 軍

(武漢理工大學能源與動力工程學院，湖北武漢 430063)

我國內陸通航水域十分廣闊，隨著內河船舶數量的日益劇增，傳統金屬艉軸承的潤滑油泄露問題也日益突出［1］。為減小泄露潤滑油對內河環境造成的污染，越來越多的非金屬軸承開始成為替代品，并且取得了很好的效果。其中水潤滑賽龍軸承以其出色的抗磨損性、自恢復的彈性及承受高壓和抗沖擊性受到了越來越廣泛的關注。

船舶水潤滑艉軸承屬于徑向滑動軸承，潤滑水隨著旋轉的軸系進入摩擦副，潤滑水膜和邊界潤滑膜承擔了局部負載，系統摩擦性能得到改善［2］。隨著轉速的提高，單位時間內進入摩擦副的潤滑水增多，混合潤滑狀態過渡到流體動壓潤滑狀態，軸頸載荷也完全由潤滑水膜承擔［3］。水潤滑賽龍軸承的潤滑數值計算以彈性流體動壓潤滑為主。經過簡化的軸承模型為線接觸模型，本文只討論穩定狀態下徑向軸承的等黏度潤滑與線接觸等溫彈性流體動壓潤滑。

1 雷諾方程與徑向滑動軸承潤滑基本方程

一般形式雷諾方程［4］如下。

式中:U、V分別為流體內某一點在t時刻x、y方向上的速度分量;h為該點的膜厚;p為壓力;ρ為流體密度;η為流體 (動力)黏度。

求解雷諾方程時，由于收斂和發散的楔形間隙同時存在于該區域，所以潤滑油膜的出口邊界在該區域發散間隙的位置無法預先得到確定的位置［5］。為此，通過尋求邊界上同時滿足壓力和壓力導數為零的點來確定出口邊界的位置，其形式如下:

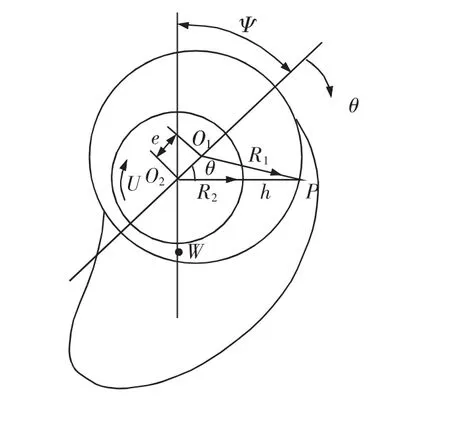
圖1 軸心位置示意圖

式中:s是求解域的邊界;n是邊界的法向。

水潤滑軸承屬于徑向滑動軸承，軸頸需帶入足夠的潤滑水進入收斂間隙中才能形成動壓潤滑，軸頸上向下的載荷與潤滑水膜向上的支撐力相平衡，其平衡位置偏于一側，如圖1所示。

偏位角Ψ為載荷W的作用線和軸承與軸頸的連心線OO之間的夾角。偏心率ε=，e為偏心

12距，c=R1－R2為半徑間隙，θ為軸相對水平位置的角度。

由圖2可知，U為軸旋轉的方向，間隙h是θ的函數。在△O1O2P，按正弦定理得:

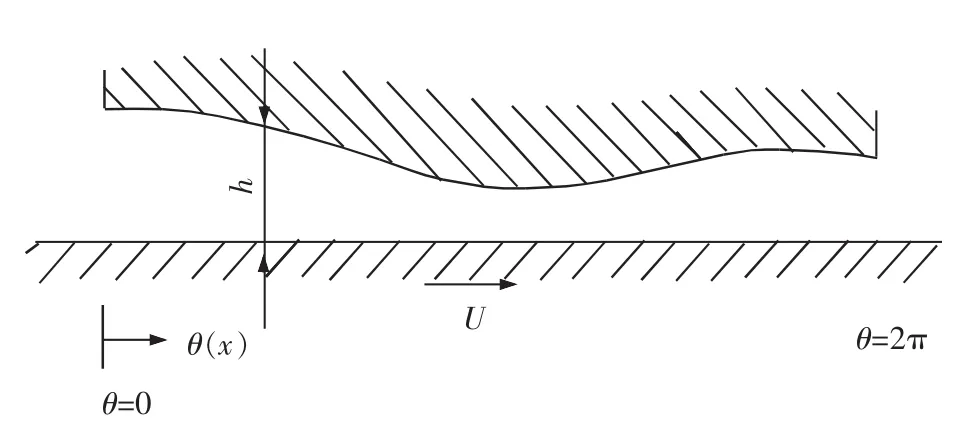
圖2 徑向軸承展開

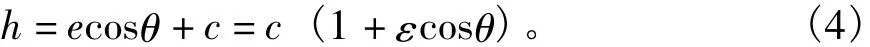
2 流體動壓潤滑數值計算

當軸頸位于偏心位置時軸承與軸頸的2個表面將會形成收斂的楔形間隙，軸頸轉動后將會攜帶潤滑水進入2個表面形成的楔形間隙當中，潤滑水在擠壓下產生流體動壓“托起”軸頸，承載軸頸上的載荷［6］。然而實船上艉軸承的工作條件惡劣，面臨的工況復雜多變，就當前潤滑理論的研究都進行了很大程度的簡化。

2.1 數學模型

水潤滑徑向軸承的流體動壓潤滑一般滿足雷諾方程［7］:

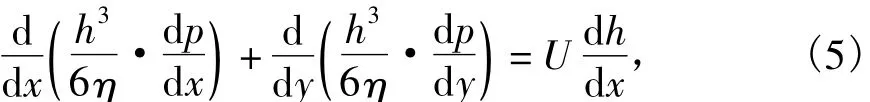
對于水潤滑徑向軸承，在軸向中間斷面上y=0，在邊緣上y=±，b為軸承寬度，而θ在0～之間變化。這個問題的邊界條件如下。

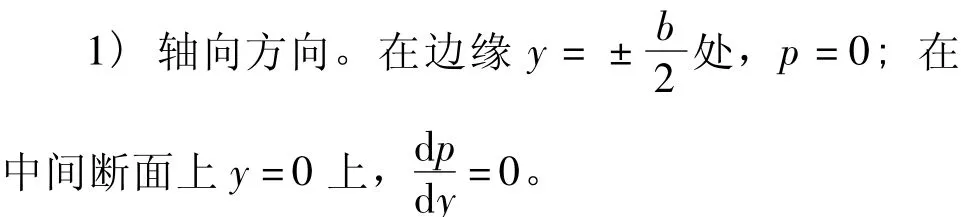
2)圓周方向。水膜起點在θ=0處，取p=0;水膜終點在發散區間內符合p=0及=0的地方。在迭代計算過程中，為確定潤滑水膜的終點位置，將p＜0的所有節點令p=0，最終就可以確定潤滑水膜的終點位置。

2.2 量綱一化

量綱一化雷諾方程為:

2.3 結果分析

在實際工況中，由于不同的載荷會導致軸頸的偏心率發生變化。為了探究不同偏心率條件下水潤滑軸承潤滑水膜壓力與膜厚的狀態，本節探究了恒定轉速為350 r/min時，不同偏心率對潤滑水膜的壓力分布和厚度的影響。

2.3.1 偏心率對潤滑水膜壓力的影響

由圖3可知轉速固定時，隨著偏心率的增加，潤滑水膜的最大壓力峰出現在潤滑水膜的不同位置:偏心率較低時，潤滑水膜的最大壓力區基本分布在軸頸正下方;隨著偏心率的增加，潤滑水膜高壓區沿軸頸的轉動方向有所移動。同時可以看到水膜最大壓力峰值也隨著偏心率的增大而增大，偏心率為0.8時，潤滑水膜的最大壓力是偏心率為0.2時的8倍以上。形成這種差別的原因是:楔形空間是形成動壓潤滑的必要條件，偏心率越大，楔形效應也就越明顯，因此潤滑水膜的壓力峰值隨著偏心率的增大而增大。

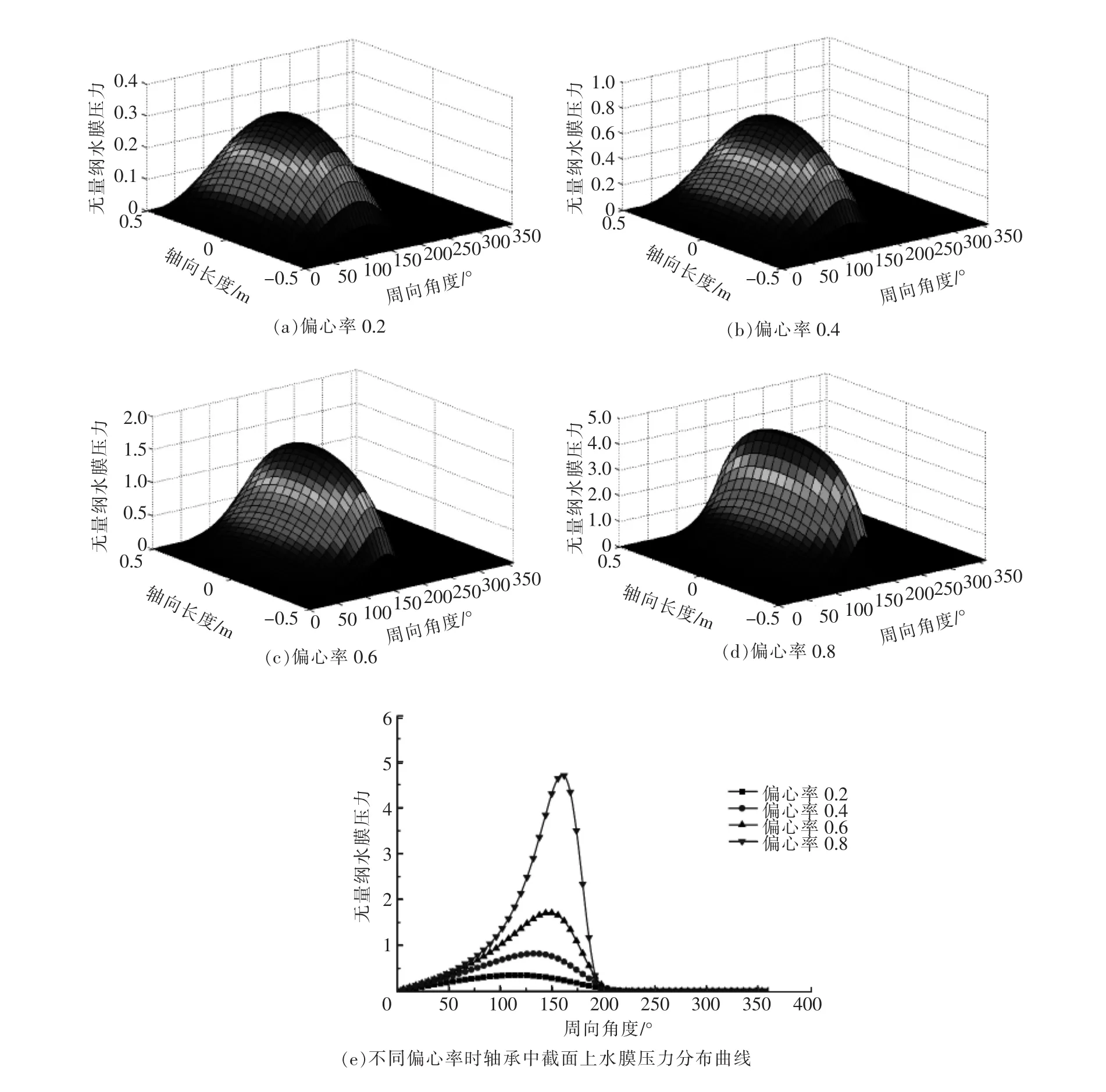
圖3 不同偏心率時潤滑水膜壓力

2.3.2 偏心率對潤滑水膜厚度的影響

由圖4可知在轉速固定時，水膜徑向截面的最小厚度隨著偏心率的增大而減小。形成這種變化趨勢的原因是隨著偏心率的增大，軸和軸頸形成的楔形間隙變小，兩摩擦表面之間的減小，隨旋轉軸頸進入楔形間隙的潤滑水減少，故水膜厚度減小。

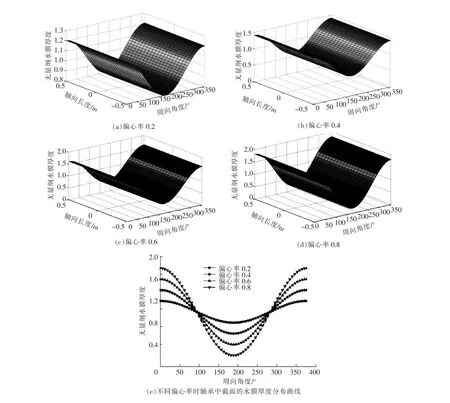
圖4 不同偏心率時潤滑水膜厚度

3 等溫彈流潤滑數值計算

彈性流體動壓潤滑 (Elasto－Hydrodynamic Lubrication)簡稱為彈流潤滑 (EHL或EHD)是摩擦學研究領域內近半個世紀以來發展的又一重要領域［8］。

3.1 基本方程與量綱一化

等溫線接觸彈流潤滑 (簡稱等溫彈流潤滑)的基本方程包括6個部分，分別是雷諾方程、膜厚方程、變形方程、粘壓方程、密壓方程和載荷方程，由于本次結果只涉及到膜厚和壓力，因此只列出膜厚方程和載荷方程。主要形式如下:

1)等溫彈流潤滑雷諾方程［9］:

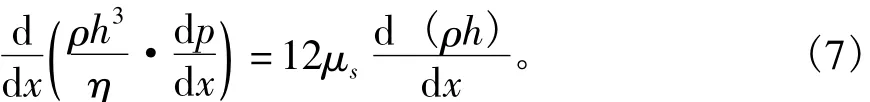
式中:μs為x方向的速度。

2)膜厚方程。在進行彈性流體動壓潤滑計算的時候，因為引進了彈性變形方程，所以在推導膜厚方程時需要將彈性變形方程疊加進去，線接觸間隙形狀如圖5所示。這時彈性圓柱體表面上的任一點x處的潤滑水膜厚度表達式為:

40例患者定期接受膀胱化療和膀胱鏡檢,8例患者未定期行膀胱化療和膀胱鏡檢,其中5例患者因自身身體素質的原因停止化療,另外3例通過家屬的溝通和后期健康教育,定期行膀胱化療,行腹壁膀胱造瘺的1例患者自理能力好,無并發癥,1例患者發生造口周圍炎經積極治療后痊愈,自理能力好。

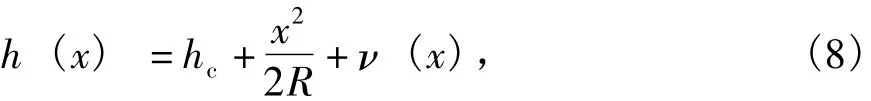
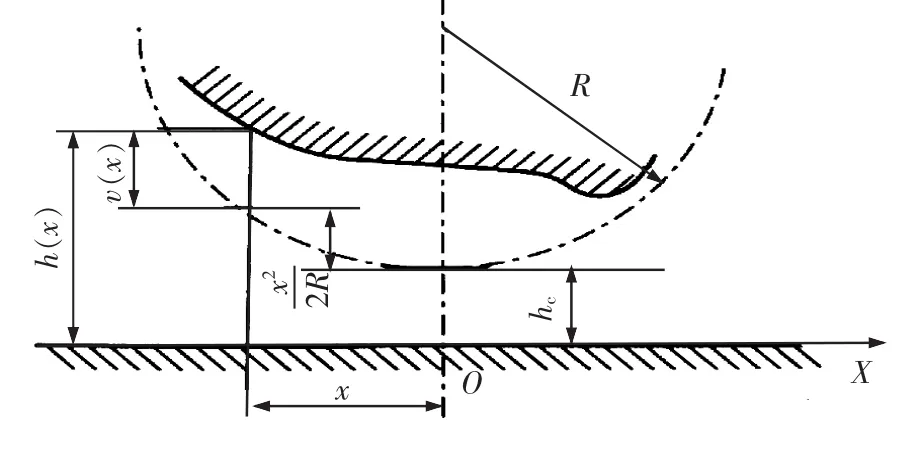
圖5 線接觸間隙形狀

式中:hc為彈性圓柱體沒有發生變形時潤滑液中心的膜厚;R為當量曲率半徑，其中外接觸取“+”，內接觸取“－”號;v(x)為由壓力產生的彈性變形位移。

3)載荷平衡方程。

由于壓力的變化會導致膜厚方程中的彈性變形，所以計算求解之前要先設定一個初始壓力分布，再計算潤滑液膜厚，最后帶入雷諾方程算出新的壓力分布。經過迭代修正與計算出新的彈性變形量和潤滑液的膜厚，多次迭代計算到相近兩次的壓力值比較接近時結束迭代。這樣就能最終計算出潤滑膜的壓力分布和計入了彈性變形的膜厚。

等溫線接觸彈流潤滑的基本方程經過量綱一化后的形式如下:

1)雷諾方程。

2)膜厚方程。

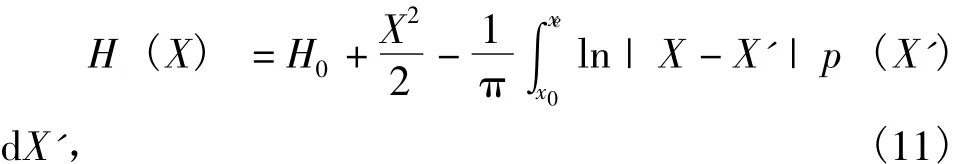
3)載荷方程。

3.2 方程的離散

采用中心和向前差分格式離散量綱一化雷諾方程，得到離散后的差分雷諾方程。量綱一化的膜厚方程和載荷方程也可以按數值積分方法寫成離散形式，這些方程形式如下所示。

1) 離散雷諾方程［10］。

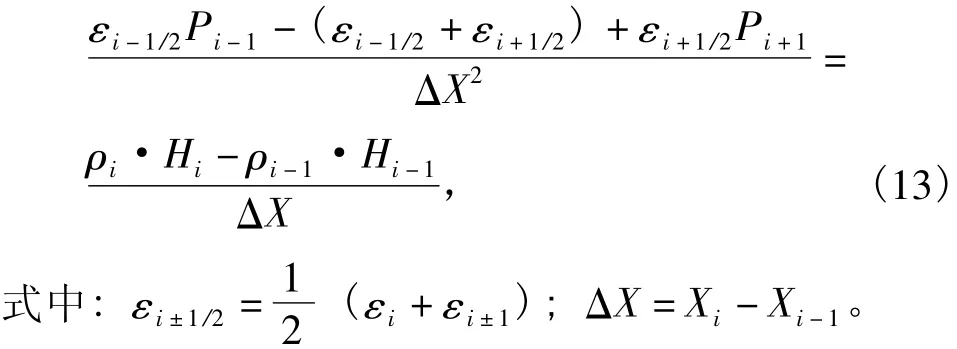
邊界條件為:入口區P(X0) =0;通過設置負壓等于0確定出口區。

2)離散膜厚方程。

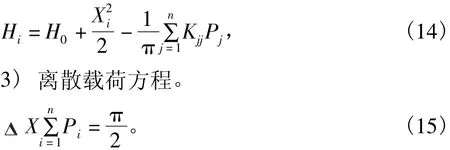
3.3 結果分析

本節研究對象是水潤滑賽龍COMPAC軸承，忽略其他影響因素。軸承直徑D1為171 mm，試驗軸的直徑D2為170 mm，賽龍/試驗軸的綜合曲率半徑R為40 mm，潤滑水為自來水，黏度為0.001 Pa·s，賽龍COMPAC材料的彈性模量為4.9×108Pa，泊松比為0.45，試驗銅軸的彈性模量為1.08×1011Pa，泊松比為0.35;賽龍/試驗軸的綜合彈性模量 E'為1.22 ×109Pa。

3.3.1 轉速對潤滑膜膜厚與壓力的影響

隨著轉速的增加，潤滑水膜壓力所增大，但增幅不是很明顯，潤滑水膜厚度增大明顯。因為隨著轉速的提高，單位時間內由旋轉軸帶入到摩擦副之間的潤滑水量增多，水膜厚度不斷增大，位于接觸區域中心的水膜壓力也不斷增大。

3.3.2 載荷對潤滑膜膜厚與壓力的影響

潤滑水膜壓力和水膜厚度受載荷的影響變化如圖6所示。載荷參數對潤滑水膜的壓力分布與厚度的影響程度各不相同:載荷對潤滑水膜壓力分布的影響明顯，隨著載荷的增加，水膜壓力減小，但減小的速率放緩，并且沒有出現第二壓力峰，水膜厚度也隨著載荷的增加而減小。

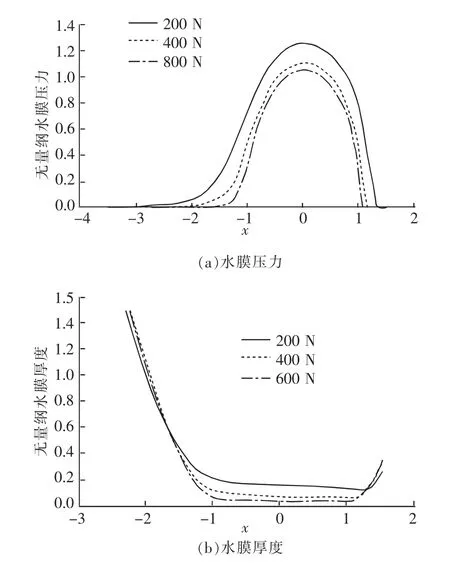
圖6 載荷對軸承水膜壓力和膜厚的影響

4 結束語

1)在徑向軸承流體動壓潤滑中，偏心率對潤滑水膜的壓力與厚度影響明顯:隨著偏心率的增大，潤滑水膜的壓力峰值不斷增大，而潤滑水膜的厚度呈現減小趨勢。

2)隨著水潤滑賽龍軸承形成彈流潤滑，潤滑水膜厚度出現輕微的頸縮現象，但壓力分布圖顯示水膜上并沒有出現第二壓力峰。

3)賽龍軸承潤滑水膜壓力受轉速的影響不是很明顯，但是水膜厚度受轉速影響比較明顯:潤滑水膜厚度隨轉速的升高而增大;賽龍軸承潤滑水膜壓力和厚度受載荷影響顯著，隨著載荷增大，水膜最高壓力變小，膜厚逐漸減小。