“接納”無理數后，如何理解實數？

江蘇省海安市城南實驗中學八（1616）班 李可欣

老師在介紹 2的歷史時，曾提到畢達哥拉斯學派的一個門徒因為發現了 2，卻不幸為之付出了生命的代價.老師還說，無理數的出現帶來了第一次數學危機.雖然我還不太懂什么是數學危機，但是像圓周率π、2這類無理數確實就在我們身邊，也廣泛出現在習題之中，我們不得不接納這類無理數，于是數系再一次擴充到實數系.經過“實數”這一章的學習，我對實數的相關知識或簡單的運算也有了一定的了解，借數學周記的機會，進行一次梳理.

1.與實數有關的概念.

2.與實數有關的運算.

在學習這一章時，老師并沒有帶領我們學習實數的運算，這令我很費解.后來我才發現帶有“根號”的綜合運算情況很復雜，需要專門學習，在后面（八年級下學期）會有專門的章節學習二次根式的運算.但是我在一些練習冊上，也見到一些帶根號的算式，比如：

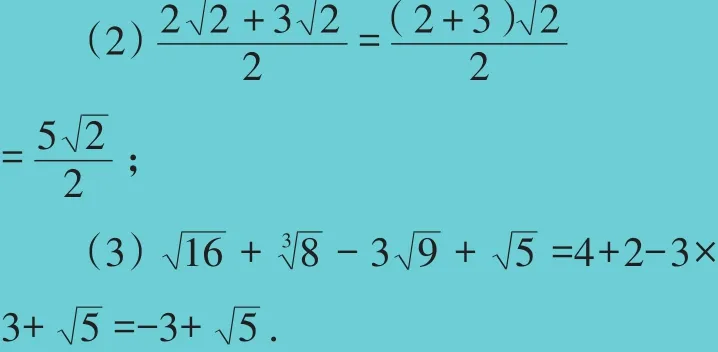
3.點的坐標也可以是無理數.

（1）將點A、B的坐標分別向左平移1個單位后得到的點A′、B′的坐標是多少？

（2）求△A′OB′的面積.

解：（1）點A（2，）、B（5，）向左平移1個單位后的坐標分別為A′（1，）、B（′4，）；

劉老師點評：引入無理數后，數系擴充到實數，需要研究很多內容．實數這一章的重點是開方運算及其概念、實數的概念、近似數等初步知識．確實如小作者所說的，實數的運算是一個大話題，教材上的“回避不談”是有一定道理的，因為實數的運算涉及二次根式的化簡與運算，這會在下學期系統學習，但是從小作者所舉題例來看，確實有理數運算中的一些經驗（如運算律）、有理數的一些概念（相反數、絕對值）、整式運算的一些經驗（如合并同類項）等都在一些簡單的實數運算中得到體現和延續．隨著學習的深入和認識的豐富，同學們終將會發現：數學在生長，但不是簡單地推倒之前的知識或性質，只是在更大范圍內接納、包容．數學在擴張的過程中追求和諧、一致．