淺談導數在高中數學中的應用

陳金保

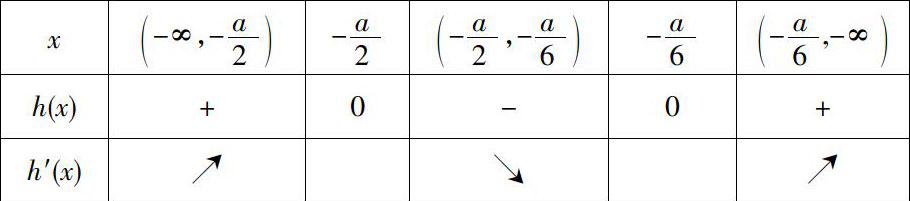
摘要：眾所周知，導數是數學學習和數學研究的基礎部分，也是人類進一步學習其他自然學科的關鍵內容。導數是建立在極限思想的基礎上，它涉及了初中、高中數學教材的各個方面，而且涵蓋了兩冊大學數學分析課本。也就是說，從小學到大學的數學學習都離不開導數，所以，對于高中生的高中數學學習，導數學習的地位是十分高的。本文從導數的定義出發，由一些例子的展示，分析了導數在高中數學中的一些重要應用，以便于學生能夠更好地理解導數的定義，接受高中導數的理論學習。

關鍵詞：導數;函數切線斜率;最值和極值

中圖分類號：G633.6? ?文獻標識碼：A? ?文章編號：1992-7711（2018）09-0105

導數如此重要，是學習數學、研究數學必不可少的一個工具，是初等數學和高等數學的一個連接紐帶。學習導數知識可以在實際應用中快速準確求出函數的切線斜率，還可以準確又簡潔的求出曲線的切線方程，也可以求出函數的最大值、最小值、極大值以及極小值，即利用導數可以解決生產和生活中常見的能用數學知識解決的最優決策和最優設計問題。導數的學習不僅僅能讓學生更好的理解函數的性質，掌握函數思想，而且在很大程度上能夠拓展學生的解題思路，并且能夠進一步提高學生分析問題的能力和解決問題的能力。

一、導數的定義分析

二、利用導數求函數的切線斜率

函數的切線斜率的求解其實是利用了導數的幾何意義，即：若函數f在點x0的導數是曲線y=f（x）在點（x₀，y₀）處的切線斜率。若表示這條切線與x軸正向的夾角，則f′（x₀）=0，即這條切線的斜率是這個夾角的正切值。從而我們可以得出結論，當f′（x₀）>0時，表明切線與軸正向的夾角是一個銳角;當f′（x₀）<0時，表明切線與x軸正向的夾角為一個鈍角;當f′（x₀）=0時表示切線與x軸平行，通過這個方法也同樣可以求出曲線的切線方程，即首先要求利用導數的幾何意義出函數的切線斜率，然后把已知的點坐標代入函數表達式中，即可求出函數的切線方程。具體有以下例子說明：

例1.已知曲線l：y=x²-2x+a，求切點為P（2，1）的曲線的方程。

解：因y=x²-2x+a，所以y′=2x-2

則當x=2時，y=a，y=2

當a=1時，點p（2，-1）在曲線上，故過點p的曲線l的切線方程可表示為：

y-（-1）=2（x-2）即2x-y-5=0。

這道例題就是先用導數求出切線斜率，然后再把已知點代入表達式。

三、利用導數判斷函數單調性問題

我們都知道，函數的單調性是指一個函數在某個區間內或者在其定義域內的單調增減性的變化規律，這是研究函數的圖形時首先需要考慮的一個關鍵性問題。而且在中學的時候，我們已經學習并掌握了函數在某個區間內或定義域內的單調增減性的定義。現在，高中數學中導數的學習讓我們更深入的了解其定義并且能更容易判斷函數增減性及確定其單調區間。

我們現在可以深入挖掘一下函數導數在函數單調性中的應用涵義，假設函數y=f（x）在點區間[a，b]中可導，則會有以下三個結論：1. 若對區間（a，b）中所有的x而言f′（x₀）>0，則f（x）在（a，b）中遞增;2. 若對區間（a，b）中所有的x而言f′（x₀）<0，則f（x）在（a，b）中遞減;3. 若對區間（a，b）中f′（x₀）=0所有的x而言，則f（x）在（a，b）中不變。由此可見，只要能夠求出函數的導數，即求出函數的切線的斜率，同時判斷它大于0的還是小于0的，就能判斷函數的單調增減性，這種方法不僅更方便，而且更加直觀。

例2.已知函數f（x）=ax²+1（a>0），g（x）=x³+bx。（1）若曲線y=f（x）與曲線y=g（x）在他們的交點（1，c）處具有公共切線，求a，b的值。（2）當a²=4b時，求函數f（x）+g（x）的單調區間。

解：（1）f′（x）=2ax，g′（x）=3x²+b，

由題知，f（1）=g（1），f′（1）=g′（1），故a+1=1+b，2a=3+b，

最后解得a=3，b=3，

所以函數h（x）的單調遞增區間為（-∞，-a/2），（-a/6，-∞）;單調遞減區間為（-a/2，-a/6）

四、利用導數求函數的極值問題

函數值由增加到減少或者是由減少到增加，都經過一個轉折點，即圖中的“峰值”點和“谷值”點，這些點是在研究函數中是十分重要的。極值的求法是這樣定義的：設函數f（x）在點x=x0及其區間左右兩側附近有定義，若對該區間內的任意點x（x=x0）恒有f（x）f（x0）成立，則f（x0）為極小值。由以下例子具體說明：

例3.設f（x）=alnx+1/2x+3/2x+1，其中a∈R，曲線y=f（x）在點（1，f（x））處的切線垂直于y軸。（1）求a的值;（2）求函數f（x）的極值。

五、利用導數求函數的最值問題

在經濟活動和日常生活中，我們常常遇到這些問題，例如：如何合理的使用原料才能達到最省，而且成本最低，效率最高或者是效益效率最好的目的的問題，這些問題在數學學習中，稱為函數的最大值或最小值問題，即最值問題。假定函數f（x）在閉區間[a，b]上連續，則必存在最大、最小值，其判定的一般步驟和方法是：1. 求導數f′（x）;2. 求方程f′（x）=0的根;3. 檢驗f′（x）在方程f′（x）=0的根的左右符號。若在根左側附近大于0，右側附近的值小于0，那么，函數y=f（x）在這個根處能夠取得極大值;若在根左側附近的值小于0，右側附近大于0，那么，函數y=f（x）在這個根處能夠取得極小值。對于在閉區間[a，b]連續，在開區間（a，b）內可導的函數f（x）對的最大值和最小值，可以首先求出函數在開區間（a，b）上的極大（小）值，并與函數定義域端點值f（a），f（b）比較，即可得出最大（小）值。由以下例子具體說明：

總之，導數的應用涉及到高中數學學習的很多內容，本文僅僅討論了導數在四個方面的應用。由此可見，高中數學中導數的學習，不僅拓展了學生學習數學和解決數學問題的思路，而且還擴展了學生的數學知識，讓學生體味到數學學習的樂趣，進一步了解數學極限思想和方法，對學生是十分有幫助的。所以，高中數學中所學的導數是我們研究高中數學的一個有力工具，在高中數學中導數的學習能夠幫助學生解決許多數學應用問題，讓學生更加牢固的掌握高中數學的基礎內容，為大家進一步的數學學習打下堅實的基礎，更有效的提高學生的數學考試成績，掌握獨特的學習方法。一句話，導數的學習是高中生學好數學、打好基礎的關鍵。

參考文獻：

[1] 高群安.運用導數巧解題[J].中學數學，2005（3）.

[2] 張圣官.導數——高中數學的一個交匯點[J].數學教學通訊，2005（4）.

[3] 常利軍.探析導數在高中數學中的應用[J].語數外學習，2013（5）.

[4] 漆建哲.導數在高中數學解題中的應用分析[D].語數外學習，2013（7）.