基于相關因子的BP神經網絡電力負荷短期預測

劉進波，周克男，任明會

（長沙理工大學 數學與統計學院 湖南 長沙 410004）

基于相關因子的BP神經網絡電力負荷短期預測

劉進波，周克男，任明會

（長沙理工大學 數學與統計學院 湖南 長沙 410004）

電力行業是一個國家非常重要的基礎性行業，電力負荷的合理預測對整個國家的安全、社會的穩定以及人民的生活都有著重大的意義。本文作者主要研究了影響短期電力負荷預測的相關因子， 并建立了基于相關因子的BP神經網絡模型，最后給出了實例分析。

電力負荷預測；相關因子分析；BP神經網絡模型

1 BP模型簡介及算法流程的推導

人工神經網絡(Artificial Neural Network—ANN)，是基于人腦結構從信息處理角度對人腦神經元網絡進行抽象的一種數學模型。人工神經網絡模型種類眾多，在電力預測方面常用的為BP模型，它由輸入層、隱蔽層、輸出層組成，其拓撲結構如圖1所示。這種模型為前饋網絡，輸入信息依次經輸入層、隱蔽層、輸出層。如果在輸出層不能得到期望的輸出，則轉入反向傳播，將誤差信號沿原來的連接通路返回，通過修改各神經元的權值，使得誤差信號最小。

圖1 神經網絡結構圖

BP算法是一種自動學習的過程，其學習過程主要包括兩個方面：

（1）輸入信息的向后傳播；（2）預測值與期望值之間誤差的向前傳播。

（1）輸入信息的向后傳播過程：

隱含層第i個節點的輸入neti為：

隱含層的第i個節點的輸出oi為：

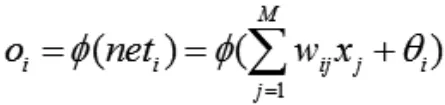
輸出層第k個節點的輸入netk為：

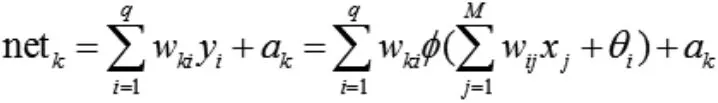
輸出層第k個節點的輸出ok為：

（2）誤差的反向傳播過程

誤差反傳其實就是將輸出誤差通過隱含層向輸入層逐層反傳，將誤差分攤給各層所有節點，直到誤差達到規定的要求，訓練即告停止。

對于樣本p的二次型誤差準則函數Ep為：

系統對p個訓練樣本的總誤差準則函數Ep為：

沿誤差函數對權值或閾值的偏導數的負方向進行修正，得出最后整理得調整公式為：

輸出層權值修正函數為：

輸出層閾值修正函數為：

隱含層權值修正函數為：

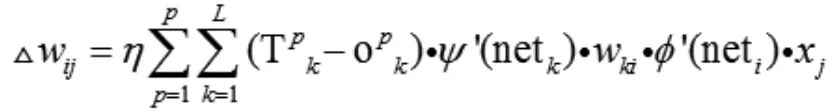
隱含層閾值修正函數為：

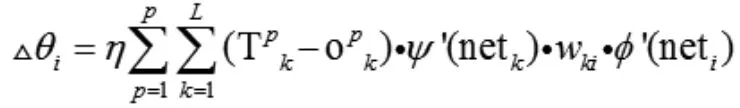
式中

wij——輸入層第j個節點到隱層第i個節點的權值，，i=1，2 ……，q，j=1，2 ……，M；

wkj——隱層第j個節點到輸出層第k個節點的權值，k=，2……L；

xj——輸入層第j個節點的輸入；

θi——隱層第i個節點的閾值；

φ——隱層的激勵函數；

ak——輸出層第k個節點的閾值；

ψ——輸出層激勵函數；

ok——輸出層第k個節點的輸出。

2 基于相關因子的短期電力負荷預測模型建立

2.1 因子的提取

短期電力負荷預測是指一年之內以月為單位或以周、天、小時為單位的電力負荷預測。大多短期電力負荷模型往往在樣本訓練過程中擬合效果較高，但在實際預預測過程中卻產生了較大的偏差，因此如何提高電力預測模型的實用性顯得尤為重要。圖2給出了電力負荷以周為單位每天的變化過程。

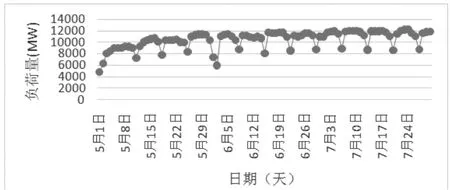
圖2 電力負荷周變化圖

由圖表可以看出，電力負荷有明顯的類周期性變化。除此之外，每日的電力負荷還將受到天氣等因素的影響，例如每天的最高溫度和最低溫度、降雨量、是否是節假日都將對當日的天氣狀況造成影響。本文結合電力負荷的實際情況，提取到的電力負荷的相關因子分別為：日期因素、日最高溫度、日最低溫度、日平均溫度、相對濕度以及降雨量。

2.2 樣本數據的量化及歸一化處理

為加快神經網絡的收斂速度，本文研究時采用S型激勵函數。并對樣本數據進行歸一化處理，避免由于輸入值較大，導致過飽和現象，影響訓練速度。本文采用指數型S型激勵函數即logsig函數，因此需要將數據歸一化到（0，1）之間。

2.2.1 相關因子數據的量化處理。日期類型不能直接作為神經元節點的輸入數據，要對其進行量化處理，在由圖表2可知，工作日用電量與雙休日（周六、周天）用電量有所不同。因此，對工作日和周末進行二分類取值，工作日取0，雙休日取1。

2.2.2 量化數據的歸一化處理。將電力負荷、量化后的日期因素、日最高溫度、日最低溫度、日平均溫度、相對濕度以及降雨量進行歸一化處理，處理方式為按（1）式將數據變成[0，1]區間變化的數據，輸出的時候再利用（2）式還原。

式中

Li——分別為第i個因子的數據，Li，i=（1，2，……8）分別表示電力負荷、量化后的日期因素、日最高溫度、日最低溫度、日平均溫度、相對濕度以及降雨量。

Limax——該因子觀測值中的最大值；

Limun——該因子觀測值中的最小值；

2.3 建立并訓練BP神經網絡

（1）輸入量選取

輸入量如圖3所示。

圖3

圖4 流程圖

每個輸入變量包括13個元素，分別為預測日之前連續7天的電力負荷、預測日量化后的日期因素、日最高溫度、日最低溫度、日平均溫度、相對濕度以及降雨量。

（2）輸出量選取。輸出量為一個數值，即預測的電力負荷值。

（3）隱層層數的確定。增加隱層的層數對網絡訓練的信息處理能力有所提高，但同時會使網絡復雜度大大增加，對網絡的性能及訓練速度產生較大的影響。由Kolmogorov定理知，在實際應用過程中，一個隱層的網絡足以解決各種復雜的實際問題，可以憑借增加隱含層節點數提高網絡處理能力。本文選取的訓練樣本數目適中，為防止建模復雜，選取一個隱層已足夠。

（4）隱層節點數的確定。隱層節點數的選取沒有固定方式，一般通過在網絡訓練中分析比較選取不同的節點數最后得出的預測結果誤差大小，然后確定合適的節點數。確定隱層節點數有以下基本的原則：試湊時，從較小節點數開始，逐漸增大，使得滿足了誤差要求的情況下，節點數較少，應盡量小于N-1(其中N 為訓練樣本數)。

（5）學習規則的確定。單純的梯度下降法學習規則往往會出現收斂速度慢，訓練時間長，有時甚至可能不收斂的問題，本文采用非線性阻尼最小二乘法(L-M)進行優化，實驗證明，L-M優化算法比單純使用梯度下降法的BP算法收斂速度快得多。

（6）學習速率的選取。如果學習速率選取太大，可能引起過調，如果選取太小，又會延長訓練時間。通常，學習速率在0.01～0.8之間選取，本文取0.1。

經過上述準備，BP神經網絡的基本建立，為后期對歷史數據的訓練以及對未來負荷的預測做好準備。結合上述步驟，基于相關因子的BP神經網絡預測模型的建立及應用過程流程圖如圖4所示。

3 實例應用

采用MATLAB神經網絡工具箱中的Newff函數按圖中的神經網絡結構創建一個三層豹BP神經網絡，網絡隱含層神經元的激勵函數為s型函數。采用L-M學習規則訓練網絡，運用trainlm函數。輸入數據，訓練網絡，進行預測。

訓練樣本的數據來自電機工程協會2016年公布的某地區的電力負荷及相關因素數據，以6月1日—6月30日的數據作為訓練樣本，其中每個訓練樣本包含13個元素，分別為預測日期前一周的電力負荷以及預測日當天的量化后的日期因素、日最高溫度、日最低溫度、日平均溫度、相對濕度以及降雨量。將數據進行歸一化處理，構建出一個13行30列的訓練樣本矩陣。訓練目標為預測當天的電力負荷構成的一個1行30列的矩陣。輸入之前建立的神經網絡，得到訓練樣本的擬合情況如圖5，由圖可知，訓練數據仿真效果較好。

圖5 仿真效果圖

用已經訓練好的網絡對7月1日至7月7日的數據進行預測，預測結果及相對誤差見表1。

表1 電力負荷預測值及相對誤差

由表中數據可知，該模型預測效果較好，平均相對誤差在5%以內，有很好的推廣價值。

4 結語

隨著科學技術的快速發展，濕度，溫度，氣溫等與電力負荷相關的影響因子的預測越來越準確，與此同時，例如日期等因子信息更是可以精確的獲得。采用基于相關因子的BP神經網絡能反映負荷自然變化的內在規律，使短期電力負荷預測的精度越來越高成為可能。本人利用MATLAB神經網絡工具箱編程，對傳統BP神經網絡算法的缺點進行了改進，使神經網絡訓練效率更高、訓練時間更短。實例計算結果表明，采用本文所使用的改進了的BP神經網絡算法的短期電力負荷預測，具有訓練速度快、預測精度高等優點。

[1]劉進波，陳鑫，李新花.基于LM算法的BP神經網絡的電力負荷短期預測[J].經濟數學，2015，32（2）34-38.

[2]倪方云，程浩忠.采用改進BP神經網絡算法預測短期電力負荷[J].供用電，2008，(02)：16-19.

[3]隋惠惠.基于BP神經網絡的短期電力負荷預測的研究[J].哈爾濱工業大學（自然科學版），2015.6：16-21.

[4]曲薇薇.基于BP人工神經網絡的電力短期負荷預測[D].東北石油大學，2011：26-32.

TM715 【文獻標識碼】A 【文章編號】1009-5624（2018）01-0211-04

國家級大學生創新創業訓練計劃項目（201610536014）；湖南省級教研教改項目《微課背景下理工類地方高校《高等數學》課程教學改革的研究與實踐》（湘教通[2016]400號）；湖南省教育廳科研項目（13C1036）；湖南省大學生研究性學習和創新性實驗計劃項目（湘教通[2016]283號）。

劉進波（1958-），男，漢，湖南長沙人，碩士，副教授。研究方向：差分方程的理論與應用，大學數學的教學研究與應用。