預應力型鋼混凝土框架彎矩調幅限值研究

李陽

(上海市政工程設計研究總院（集團）有限公司，上海市 200092)

0 引言

對于預應力型鋼混凝土靜定結構，國內也已有不少學者做過研究。但對于預應力型鋼混凝土超靜定結構得研究并不多。本文結合兩榀預應力型鋼混凝土框架結構豎向靜力試驗，總結現有規范對預應力超靜定結構的限值的討論，對預應力型鋼混凝土結構調幅限值做如下探討。

1 已有規范對預應力超靜定混凝土結構的規定討論

國內外對于預應力超靜定結構的內力重分布以及彎矩調幅都有一定的研究和明確的規定。

（1）美國ACI318-08規范[3]

美國ACI-318R-08第18.10.3規定，用彎矩計算強度時，彎矩應是由預壓力（荷載系數為1.0）產生的彎矩與設計荷載產生的彎矩的和，即荷載彎矩Mload和張拉引起的次彎矩Msec。當按塑性方法進行設計時，需要對兩者之和進行調幅，即

式中：M為支座控制截面的彎矩設計值；Mload為支座控制截面處由設計荷載彈性分析所產生的彎矩設計值；Msec為支座控制截面次彎矩；β為彎矩調幅系數。

B18.10.4.1規定了任何荷載作用下通過彈性理論計算的負彎矩調幅系數的限值：

βi為等效矩形應力塊系數，規范10.2.7.3規定，當時，βi取值線性減少，強度沒超過 7 MPa 時，βi降低0.05，但取值不小于0.65。

（2）歐洲規范 EN1992-1，EN1992-2[4-5]

EN1992規范5.5采取線彈性分析，并考慮有限的內力重分布，內力重分布的取值取決于鋼筋等級、混凝土相對受壓區高度和混凝土強度等級。EN1992根據的fi/fy特征值以及最大荷載下的特征伸長率 εuk將鋼筋分為 A、B、C 三級。A 類鋼筋（fi/fy）k≥1.05，εuk≥2.5%，B 類鋼筋（fi/fy）k≥1.08，εuk≥5.0%，C 類鋼筋 1.35＞（fi/fy）k＞1.15，εuk≥7.5%。EN1992 考慮內力重分布的方法是將承受最大負彎矩的截面彎矩乘以折減系數δ，其中，由于EN1992-1和EN1992-2適用范圍不同（EN1992-1適用于建筑結構，EN1992-2適用于橋梁結構），兩者對于預應力超靜定結構的內力重分布的規定也有所區別。

EN1992-1規定：

εcu2為混凝土極限壓應變，當fck≤50 MPa取0.0035。

EN1992-2規定：

式中：d為截面有效高度。

規范還規定當結構構件轉動能力不足時不應當考慮內力重分布。

（3）澳大利亞規范AS3600-2009[6]

澳大利亞規范AS3600-2009的6.2.7條規定當截面具有足夠的轉動能力時，可以對截面進行調幅設計。根據鋼筋延性的不同，將鋼筋分為低延性 L（Low）、中等延性 N（Normal）、高延性 E（Earthquake）三類。規范建議進行調幅設計的結構使用中等延性的鋼筋。調幅設計時應對外荷載彎矩和次彎矩之和進行調幅。

定義相對受壓區高度ku=xn/h0，

AS3600-2009規定：

當ku≤0.2時，調幅值β不超過30%；

當 ku＞0.4 時，β≤75（0.4-ku）%；

當ku＞0.4時，不應當進行調幅設計。

調幅設計中，需要注意調幅后的結構彎矩要符合靜力平衡，同時對結構的延性和和抗沖切承載力要做進一步的分析。

（4）我國混凝土規范規定

《混凝土結構設計規范》（GB 50010-2002）[7]6.1.8規定對后張法預應力混凝土框架梁及連續梁在滿足縱向受力鋼筋最小配筋率的條件下當截面相對受壓區高度ξ≤0.3時可考慮內力重分布支座截面彎矩可按10%調幅并應滿足正常使用極限狀態驗算要求。當ξ＞0.3時不應考慮內力重分布。

《混凝土結構設計規范》（GB 50010-2010）[8]對此條做了修改并給出了具體公式，10.1.8條規定，對允許出現裂縫的后張法有粘結預應力混凝土框架梁及連續梁，在重力荷載作用下按承載能力極限狀態計算時，可考慮內力重分布，并應滿足正常使用極限狀態驗算要求。當截面相對受壓區高度不小于0.1且不大于0.3時，其任一跨內的支座截面最大負彎矩設計值可按式（2）確定，且調幅幅度不宜超過重力荷載下彎矩設計值的20%。

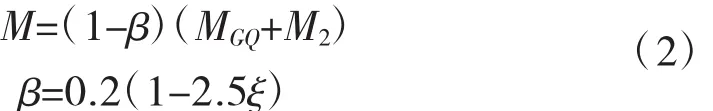
式中：M為支座控制截面彎矩設計值；MGQ為控制截面按彈性分析計算的重力荷載彎矩設計值；ξ為截面相對受壓區高度；β為彎矩調幅系數。

2 預應力型鋼混凝土框架豎向靜力試驗研究

2.1 試驗基本信息

試驗所用試件是兩榀大尺度后張有粘結預應力全型鋼混凝土框架XGKJ1和XGKJ2。兩榀框架梁截面縱筋配筋不同，預應力度不同。框架柱中線長度為8.2 m,，預應力筋均配置2Φs15.2鋼絞線（fptk=1 860 N/mm2），混凝土 C40，XGKJ1 縱筋采用6Ф18（HRB400），預應力度 0.50；XGKJ2 縱筋采用6Ф22（HRB400）預應力度 0.40，內置型鋼為 Q235，連接螺栓M20為8.8級摩擦性高強螺栓。柱內型鋼上下翼緣、梁端型鋼上翼緣設兩排Ф19@200栓釘。試驗框架采用兩點集中對稱的同步分級加載方式。跨中純彎段長度為2 700 mm。試驗構件配筋見圖1。

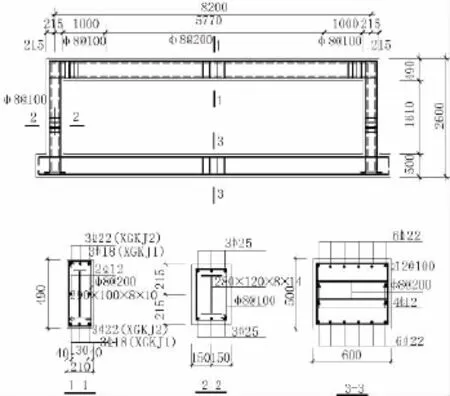
圖1 試驗構件設計（單位：mm）

試件設計參數見表1。

兩榀框架均選用C40混凝土進行澆筑。在試驗中，型鋼梁柱外側均設置足夠的抗剪連接件來防止構件加載過程中型鋼和混凝土之間發生粘結滑移。

兩榀試驗框架的荷載-位移曲線見圖2。

表1 試件設計參數

圖2 試驗框架荷載-位移曲線

利用ABAQUS有限元軟件對試驗框架進行模擬分析。在梁到達極限狀態的時候，混凝土塑性應變見圖3，與試驗破壞模式基本吻合。

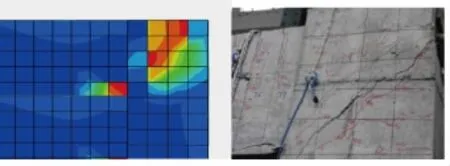
圖3 XGKJ1破壞階段混凝土塑性應變與試驗現象對比

XGKJ1、2的荷載-位移曲線數值模擬結果與試驗結果對比見圖4、圖5。

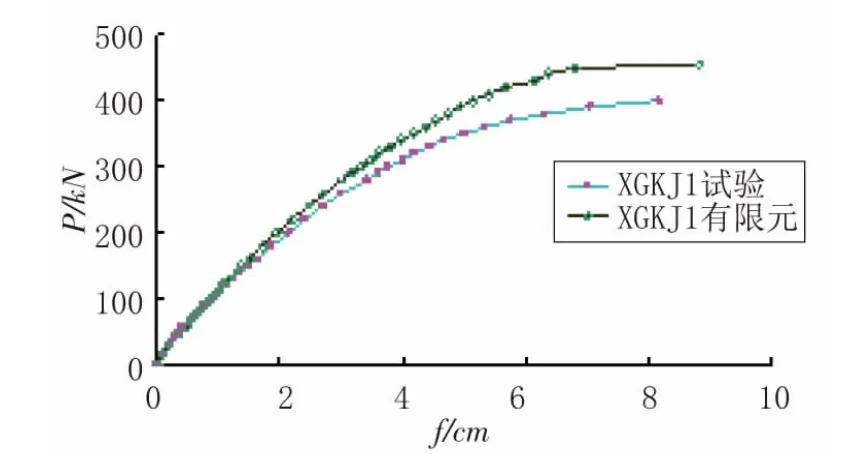
圖4 XGKJ1加載點荷載撓度曲線試驗與有限元對比

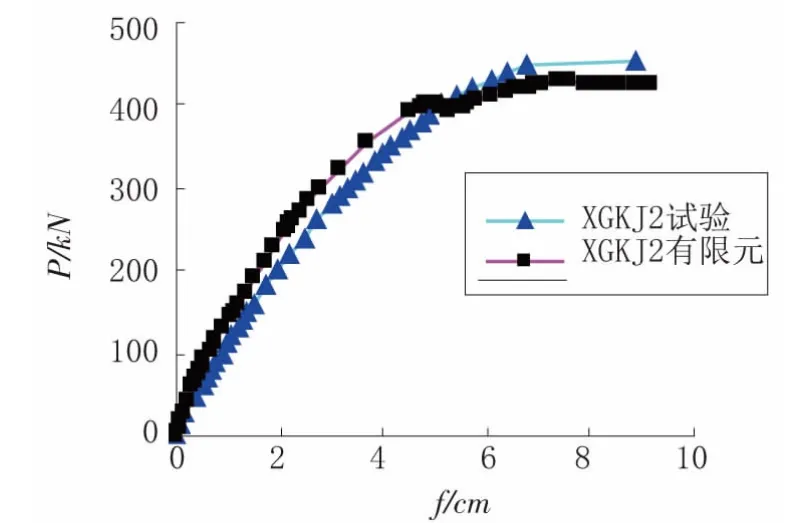
圖5 XGKJ2加載點荷載撓度曲線試驗與有限元對比

通過圖4、圖5可以看出，在ABAQUS中所建立的有限元模型與試驗實測在加載點的荷載位移曲線吻合較好。在試驗加載的初期階段，數值模擬的荷載撓度曲線斜率大于試驗的荷載撓度曲線。在框架鋼筋進入屈服階段時，荷載撓度曲線較前期變得平緩。快到達極限承載力時，有限元模擬的荷載位移曲線比試驗值略小，極限承載力Pu值與試驗所測值相比誤差最大在7%左右。可見此有限元模型基本能夠模擬預應力型鋼框架的受力性能。

2.2 試驗框架的內力重分布探討

在本文中，將預應力度以預應力強度比來表示，表示預應力筋所承擔的彎矩占受拉鋼筋與預應力筋總體承載彎矩的百分比。具體公式如下：

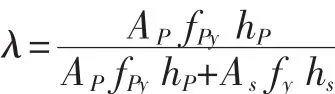
對試驗所作的兩榀框架進行計算。在極限狀態的內力重分布中，對于預應力框架結構，將次彎矩對結構的影響也看做是一種調幅[9][10]，則總調幅系數β包括兩個部分：次彎矩調幅βsec和荷載彎矩調幅βload，將次彎矩調幅又劃分為豎向等效荷載次彎矩調幅βsec1和軸力引起的次彎矩的調幅βsec2兩個部分。根據定義，則有

式中：Mload為彈性計算的荷載彎矩設計值；Ma為調整后的彎矩設計值；Msec為初始次彎矩。

對于單層單跨的預應力框架結構，次彎矩在梁端與彈性計算負彎矩值相反，即減小了彈性負彎矩設計值，為正調幅。將試驗框架截面的彈性計算彎矩、調整后彎矩以及彎矩調幅系數計算見表2。

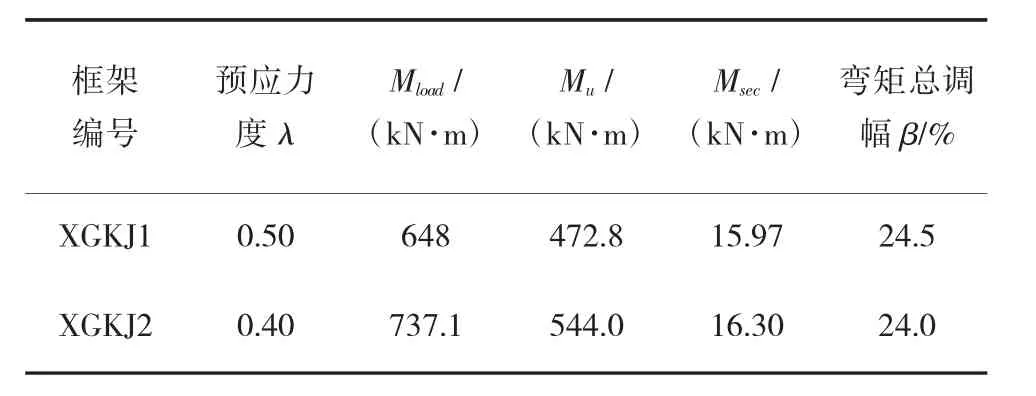
表2 試驗框架1、2調幅計算

可以看出，兩榀試驗框架的支座彎矩調幅均在0.30左右，其中，次彎矩調幅約占總調幅值的10%。同時隨著預應力度的增大，框架的支座彎矩總調幅會有所增大。

3 預應力型鋼混凝土框架支座彎矩調幅研究

（1）框架梁、柱中型鋼含鋼率對支座彎矩調幅的影響

通過改變模擬預應力型鋼框架中的含鋼率，從而對框架支座彎矩調幅值的變化做研究。設計模擬框架XG1，梁中型鋼尺寸190×50×8×10，含鋼率為2.29%，柱中型鋼尺寸180×60×8×10，含鋼率為1.84%；模擬框架XG2，梁中型鋼尺寸為290×100×8×10，含鋼率為4.04%，柱中型鋼尺寸為280×120×8×14，含鋼率為3.32%；模擬XG3，梁中型鋼尺寸為370×150×8×10，含鋼率為5.64%，柱 350×180×8×14，含鋼率為 4.62%。

XG1，XG2，XG3的加載過程中荷載位移曲線見圖6。

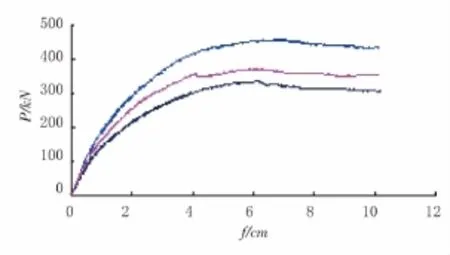
圖6 XG1、XG2、XG3的荷載位移曲線

從圖6可以看出在相同的截面下，型鋼率增大顯著增大了預應力型鋼混凝土框架的結構承載力。

在截面不變的情況下，改變框架梁柱中型鋼含鋼率，支座彎矩調幅值的變化趨勢見圖7。

圖7 彎矩調幅值隨著型鋼含鋼率變化趨勢圖

隨著框架梁柱中型鋼含鋼率增大，框架支座彎矩調幅能力也同步增大。可見在截面尺寸一定的前提下，型鋼在不僅能夠為預應力混凝土結構提供更大的極限承載力，同時也能提供更好的延性。但結構中的型鋼框架也不宜過大，以符合結構在施工中的要求。

（2）混凝土強度對支座彎矩調幅的影響

設計一組模擬框架，改變框架的混凝土強度等級，研究混凝土強度等級變化對預應力型鋼混凝土框架支座彎矩調幅值的影響。混凝土強度等級對預應力型鋼混凝土框架支座彎矩調幅值的影響見圖8。

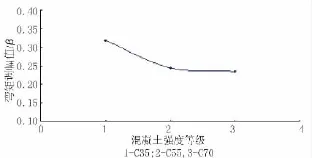
圖8 彎矩調幅值隨著混凝土強度等級變化趨勢圖

在強度等級為C35的模擬框架中，結構極限承載狀態的破壞標志是端部及跨中混凝土的壓潰，預應力筋同時也達到了其條件屈服強度，型鋼框架梁端上下翼緣屈服，而梁端部斷面的受拉受壓縱筋均未達到屈服狀態，可能也是由于低強度混凝土的應用所致。而在強度等級為C55以及C70的模擬框架中，框架縱筋強度都能較好的利用。這一點也是和上述規范的規定是相符的。由于強度等級的不同造成了本組模擬框架的破壞模式也有所不同，C35的模擬框架極限截面彎矩是小于理論值。C35等級框架和C55等級框架支座彎矩調幅值相差7%左右，C55和C75等級框架支座彎矩調幅值只有1%的差值。可以看出，只有在該種結構中同時使用高強度混凝土（建議C40以上）以及高強鋼筋，才能充分的利用材料的性能。隨著混凝土強度等級的提高，預應力型鋼混凝土框架調幅限值也隨之減小。這在歐洲規范EN1992-1、EN1992-2中也有所體現。

（3）相對受壓區高度對支座彎矩調幅值的影響

當預應力度不變，截面的相對受壓區高度改變時，同樣設計一組預應力型鋼框架，以研究截面的相對受壓區高度改變對支座截面彎矩調幅的影響。

相對受壓區高度的增大，會減小截面的延性。在進行截面設計時，截面受彎延性，一般是采用延性系數來μ?表示。所謂截面延性，是指截面在受拉鋼筋屈服的后，截面承載力無明顯變化的情況下進一步承受變形的能力，一般用式（4）來表示：

式中：Φu是極限狀態時截面的轉角；Φy是相應于受拉鋼筋應力達到屈服強度時截面的轉角。對于一個給定的截面來說，當受拉鋼筋位置給定時，Φy則為定值。，式中x為截面的實際受壓區高度。截面的延性系數隨著相對受壓區高度的增大而減小。

支座彎矩調幅隨著相對受壓區高度變化的趨勢見圖9。

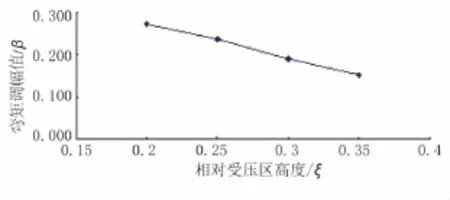
圖9 彎矩調幅值隨著相對受壓區高度的變化趨勢圖

4 預應力型鋼混凝土框架支座彎矩調幅建議

以本文工作為基礎，結合國內外規范，以調幅截面相對受壓區高度ξ為橫坐標，以截面的彎矩調幅值β為縱坐標，將試驗框架梁截面調幅值和模擬框架梁截面調幅值繪制，可以得到預應力型鋼混凝土框架梁端彎矩調幅建議曲線，見圖10。

對預應力型鋼混凝土框架結構調幅能力提出如下建議：建議使用的混凝土強度等級不小于C40，以充分利用材料強度。在預應力型鋼混凝土框架結構塑性設計時，框架支座截面相對受壓區高度不超過0.3。預應力度對結構支座彎矩調幅影響很小，在設計中可以不考慮。考慮對彈性彎矩計算值以及次彎矩組合值進行調幅，注意由于約束的不同，次彎矩能提供正調幅也能提供反調幅。有效預應力以及線型變化通過次彎矩在調幅設計中進行考慮。通過本文試驗框架以及模擬框架的調幅值分布統計，當調幅值限定為不大于20%時，可以有89%左右的保證率。當型鋼含鋼率較大或相對受壓區高度較小時，建議的調幅值還可進一步增大。

5 結論

（1）ABAQUS中損傷塑性模型具有較好的收斂性，能夠較好的模擬混凝土的力學性能。

（2）試驗表明，框架梁相對受壓區高度在0.26時，預應力型鋼框架的支座彎矩調幅值在25%左右。

（3）對不同影響因素變化下幾組框架的具體分析表明，預應力框架型鋼含量在一定程度內增大時，不僅能夠增大結構的承載力，還能增大結構的延性；對預應力型鋼框架支座彎矩調幅能力影響最大的是支座截面的受壓區高度，截面的受壓區高越大，截面的延性越差，支座彎矩調幅能力相應降低。