通道中行人-機動車相互作用機理的建模和模擬?

張稷韋艷芳董力耘

1)(上海大學,上海市應用數學和力學研究所,上海 200072)

2)(玉林師范學院物理科學與工程技術學院,玉林 537000)

3)(上海市力學在能源工程中的應用重點實驗室,上海 200072)

(2018年8月7日收到;2018年10月8日收到修改稿)

本文研究了通道中行人與車輛同向或反向運動時的人車相互作用.車輛運動的描述采用細化的確定性元胞自動機模型,而行人流則采用考慮背景場的格子氣模型.車輛及其影響區被視為一種可移動的障礙物,形成動態變化的背景場,可以更好地反映人車之間的相互作用.通過數值模擬得到典型參數下的行人流基本圖以及平均車速隨行人密度的變化曲線.人車反向時行人流基本圖中存在兩個臨界密度,其間的行人流量-密度曲線呈線性分布,曲線斜率k主要依賴于車輛寬度和行人預判時間,而平均車速近似為k,即反向車輛形成的移動瓶頸和行人擁堵向上游傳播的速度是一致的.文中進一步考察了行人預判時間、車輛寬度及限速對人車混合交通流的影響.人車同向時,這三個參數的影響都不明顯.人車反向時,當車輛寬度較小,即使在很高密度下,車輛仍可以前行,而更大的行人預判時間也有助于車輛的運動.

1 引 言

近年來,國內外眾多學者開展了大量的交通流觀測、建模、模擬和應用研究等工作,對機動車流和行人流的研究都取得了顯著的進展[1?4].在交通流的微觀建模中,元胞自動機模型得到廣泛應用:機動車流的NaSch模型[5]和可以描述三相交通特征的模型[6,7];行人流模型包括基于背景場的元胞自動機模型[8,9]和格子氣模型[10].元胞自動機模型通常采用并行更新模式,因此需要解決多個行人同時進入一個目標元胞的沖突問題.背景場元胞自動機模型的一個突出優點是有效解決了復雜環境中行人的尋徑問題[11,12].格子氣模型可以視為一種特殊的元胞自動機模型,通常采用隨機串行更新方式,其優點是可以避免行人之間的沖突.眾多的機動車和行人流模型為深入研究人車混合交通流奠定了堅實的基礎.

最近,行人和車輛之間的相互作用已成為交通流研究關注的熱點之一.最常見的人車相互作用發生在行人橫穿道路時,其特點是人群與車流運動方向相互垂直,與之相關的研究也最多.Helbing等[13]研究了橫穿街道的行人與車輛之間相互作用導致的振蕩模式.段后利和張毅[14]建立了由行人元胞自動機子模型、機動車元胞自動機子模型及相互干擾子模型三部分構成的行人過街模型,用于分析有信號燈人行橫道處的人車混合交通流的特性.孫澤和賈斌[15]通過引入行人和機動車的沖突干擾規則,建立了能夠描述人行橫道處機動車和行人相互干擾行為的元胞自動機模型.余艷等[16]基于VDR模型,建立了行人與機動車相互干擾的元胞自動機模型,研究開放邊界條件下有/無紅綠燈控制時,車輛產生概率、消失概率和綠信比對車流和行人流的影響.Zheng等[17]研究了行人亂穿馬路的行為以及司機對此類違章行為的反應.Li和Sun[18]提出改進的元胞自動機模型,探討了車輛為避免撞上行人所采取的換道行為對交通流量、能量損耗、行人穿越行為以及交通安全的影響.Gorrini等[19],Chen等[20]和Lu等[21]研究了無信號燈人行橫道處行人與機動車相互作用行為.2018年,Khallouk等[22]提出改進的元胞自動機模型,對簡化的無信號燈十字交叉口人行橫道處行人與機動車的相互影響進行研究.

另一種典型情況是人群和車輛的混合交通流.這在亞洲一些中小城市以及我國農村鄉鎮中尤為常見.農村鄉鎮上道路狹窄,往往只有一條機動車道,當車輛在擁擠的街道上行駛時,常常出現人群、非機動車和機動車的混合交通流,這種情況下往往是雙向的行人流.在大型群體活動散場時,密集的人群進入活動場館周邊的街道,或者當隧道內發生事故而進行人群疏散時,也會發生人車混行的情況,這時通常會出現單向運動的人群,本文主要研究這種情況.相比于行人橫穿馬路,目前此類研究相對較少.Jiang和Wu[23]首次采用行人流格子氣模型和簡化的車輛運動模型研究了通道中的人車相互作用,考察行人密度、車輛大小和位置對車輛運動的影響.發現車輛逆行時,在通道中間行駛更快;而人車同向時,則沿著通道壁行駛更快.Jiang和Wu[24]進一步考慮了Vmax>1的情況,并引入了車輛影響區域的概念.他們發現對于給定的人數,存在一個臨界最大車速,還發現存在車輛從自由運動態到低速運動態的切換現象.在Jiang和Wu[23,24]的工作中主要關注了車輛在人群中的運動.本文認為應該給予行人運動同等的重視,尤其是車輛附近行人的行為.由于車輛可以移動,出于安全性考慮,車輛的影響還不限于自身的大小.如何準確刻畫車輛附近行人的避讓行為是描述人車相互作用的關鍵,目前對于這方面的系統研究還較少.

本文擬細致研究通道內行人和車輛之間的相互作用.車輛運動描述采用細化的確定性NaSch模型[5],而行人運動描述則采用基于背景場的格子氣模型[25].把車輛及其影響區域作為移動的障礙物,通過在格子氣模型中引入背景場來更好地反映行人在車輛周圍的避讓行為,并且該背景場是動態變化的.基于該行人-車輛耦合微觀模型,對人車混合交通流進行數值模擬,通過行人運動基本圖以及平均車速隨行人密度的變化關系給出行人和車輛運動的統計特征,并采用人車空間分布圖和短時平均車速時間序列來詳細刻畫人車之間的干擾機理.文中還進一步研究行人預判時間、車輛最大限速以及車輛寬度等3個重要參數對通道內人車混合交通流的影響.

2 行人-車輛運動的微觀離散模型

2.1 基本假設

本文僅研究通道內單向運動人群與單一車輛的相互作用,可以看作隧道內人群疏散的情況.當大型活動散場時,考慮到街道兩側建筑物對人群運動的限制,也可以簡化成這種情形,模型示意圖如圖1所示,基本假設如下:

1)行人運動限制在水平通道內,通道上下兩側為剛性壁,不可穿越,見圖1.行人可以從左往右走,也可以從右往左走,但本文不考慮雙向行人的情況.本文引入行人預判時間τ來表示車輛運動對行人的影響,其數值越大,相同車速下車輛的影響范圍就越大,從而行人可提前避讓車輛.該參數反映了行人對自身安全的敏感程度.

2)車輛沿著通道的中軸線從左向右運動.暫不考慮車輛偏離通道中軸線的情況.車輛對行人的影響不僅限于它在通道中占據的面積,還與它的自身速度和行人的預判時間有關.車輛速度越大,行人的預判時間越長,則車輛對前方的影響范圍就越大.同時車速還會影響兩側的行人,車速越大,行人須離車輛越遠,以保障安全.

3)采用周期邊界條件.即行人(車輛)從通道一側邊界離開,就立即從另一側進入通道.

2.2 行人運動模型

1)確定背景場

本文考慮兩種情況:1)行人和車輛運動方向相同;2)行人和車輛運動方向相反.在下文中分別用Case 1和Case 2表示.對于向右(左)運動的行人而言,右(左)側邊界產生一個背景場(floor field),如圖1(b)和圖1(c)所示.右(左)行行人在該背景場的驅動下向右(左)運動.本文將車輛作為一種可以移動的障礙物,因此車輛的影響不限于它自身所占面積,示意圖見圖1(a).

圖1 車輛及其影響區和背景場示意圖 (a)車輛及其影響區(灰色);(b)人車同向時的背景場;(c)人車反向時的背景場;(b)和(c)中白色區域(車輛的影響區)外為背景場;行人在背景場的作用下由淺灰色區域向深灰色區域運動Fig.1.Sketches of the vehicle(and its influence area)and floor fields:(a)The vehicle and its impact area(grey)in Case 2;(b)floor field in Case 1;(c)floor field in Case 2.Outside area of the white area(i.e.,impact area)in panel(b)or(c)is the floor field.Pedestrians are driven to move from light-grey part to black part under the floor field.

車輛影響范圍的縱向(運動方向)長度?x和橫向長度?y的表達式如下:

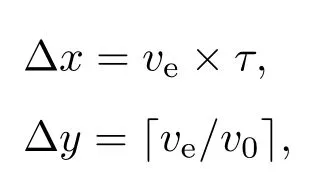
其中ve=min(v(t)+1,Vmax),v0=10,[···]表示向上取整函數.上式表明,車輛的期望速度ve越大、行人的預判時間τ越長,在運動方向上的影響范圍就越大;此外車輛的期望速度還產生橫向的影響,即ve越大,對于車輛兩側的行人而言,橫向的安全距離就越大.Jiang和Wu[24]采用了如下形式的影響區:?x=1+v2/(2a?),?y=1,a?為車輛減速時的加速度,即車輛前方的影響范圍是車速為v的車輛以a?減速到零時駛過的距離,而橫向的影響范圍則是給定的.

本文采用Varas等[11]提出的方法來計算內部有障礙物區域的背景場.將車輛的影響區作為一個障礙物,而不僅是車輛本身所占據的元胞,如圖1(b)和圖1(c)所示.由于車輛位置和影響區的大小隨著時間改變,每一時步都要重新計算背景場,因此計算量有所增加.

2)計算背景場的梯度,確定行人的期望運動方向

對于車輛影響區以外的行人,如果他所在位置處背景場梯度沿水平方向的分量大于沿垂直方向的分量,則沿水平方向運動,反之則沿垂直方向運動.

對于處于車輛影響區(其中無背景場)的行人,他們傾向于盡快離開該區域,因而根據其相對于中軸線的位置,選擇向上或向下運動.

3)行人根據相鄰元胞的狀態確定目標元胞

當行人的期望運動方向確定后,他與周圍行人或車輛的局部相互作用采用格子氣模型[10]來描述,其中行人偏移概率用D表示.由于采用格子氣模型避免了處理行人沖突問題,可以提高計算效率.

4)采用隨機串行更新方式逐一更新行人的位置.

2.3 車輛運動模型

本文采用細化的確定性NaSch模型,即車道劃分為長為0.4的元胞(即與行人所占元胞大小一致).相應規則如下:

1)加速,vi=min(vi(t)+1,Vmax);

2)減速,vi(t+1)=min(vi,di(t));

3)運動,xi(t+1)=xi(t)+vi(t+1).

這里Vmax為車輛限速,di(t)是車輛與其正前方最近一個行人的距離.

2.4 人車相互作用

對于車輛而言,當它在通道中行駛時,為確保不發生碰撞事故,只要前方有行人,車輛必須在碰到行人之前停下.另一方面,車輛在運動時,其影響區以及所形成的背景場會驅使前方行人避讓車輛,車速越快,其影響區就越大.當行人比較謹慎而采用較大的預判時間時,相同車速下車輛的影響區隨預判時間增大.因此,整個車輛影響區可視為一個隨速度和預判時間而動態變化的障礙物.

對于行人而言,當他發現車輛接近時,會根據車速做出預判,提前向兩側避讓,以免發生碰撞.如果避讓不及或者由于其他行人阻礙而未能進入安全區域,就會阻礙車輛的運動.

3 數值模擬與分析

3.1 參數設置

把通道離散成由大小為0.4 m×0.4 m的元胞構成的二維網格,尺度為L×W.一個行人最多可占據一個元胞.本文僅研究通道內只有一輛車的情況.設車輛的長度為l,寬度為w.則通道內最多可以容納N=L×W?l×w人.模擬中以下參數保持不變:L=500,W=10,l=10,D=0.9.模型的可變參數為:車輛限速Vmax,可取1,5,10,15和20;車輛的寬度w,可取2,4和6,分別相當于摩托車、小轎車和公交車的寬度;行人的預判時間τ,可取0,1,2,3和4.

初始時刻,一輛車停在通道的中心,密度為ρ的行人隨機分布在通道內.行人密度ρ定義為

其中Np是通道中行人的數量.

行人的平均速度U定義為

其中ui(t)是第i個行人在t時的速度,T0是系統達到穩態的時間,T是計算速度平均值所用的總時間步長.

行人流量J定義為

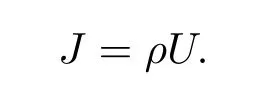
由于只有一輛車,其平均速度V定義為

其中v(t)是車輛在t時的速度.

3.2 典型參數下模型的基本性質

為了把握系統的基本性質,首先研究一組典型參數(Vmax=5,w=4,τ=3)下的人車相互作用.圖2給出人車同向和反向兩種情況下的行人流基本圖,并進行比較.

圖2 兩種情況下的行人流基本圖 (a)速度-密度曲線;(b)流量-密度曲線Fig.2.Fundamental diagrams for pedestrian in both cases:(a)Average speed of pedestrians against pedestrian density;(b)flux of pedestrians against pedestrian density.

由圖2可見,當人車同向時,行人平均速度隨著密度的增加而單調光滑地減小,流量曲線則呈現出隨密度增加先增大而后減小的趨勢,最大流量出現在ρ≈0.53附近.當人車反向時,發現存在兩個臨界密度ρ1和ρ2.當ρ<ρ1和ρ>ρ2時,兩種情況下的速度(流量)-密度曲線基本重合,表明在低密度和很高密度下,行人的運動受車輛運動方向影響不明顯,這與日常經驗是一致的.當行人較少時,行人會由于避讓車輛而沿通道兩側行走且兩側也有足夠空間,因此人車運動都較為通暢;而當行人密度很高,車輛也只能緩慢行進,甚至停滯不前.當ρ16ρ6ρ2時,反向運動行人流平均速度低于同向情況.在流量-密度曲線上則呈現線性下降的趨勢,其斜率為

該斜率近似為一個常數(k6 0),表明行人擁堵向上游傳播的速度,即反向車輛運動所形成的移動瓶頸的速度,因為擁堵發生在瓶頸處及其下游區域.該斜率依賴于車輛的寬度、行人的預估時間等參數,將在后面給出.

圖3 平均車速隨行人密度變化曲線Fig.3.Average speed of the vehicle against pedestrian density.

圖3 為平均車速隨行人密度的變化,可以看出,當人車同向時,平均車速隨行人密度的增加而逐漸下降.而人車反向時,當行人密度很小時,平均車速僅比人車同向時下降略快;當行人密度進一步增加時則迅速下降.當ρ>ρ1時,平均車速突降,表明車輛前方上游附近開始出現行人的擁堵,車輛只能以很低的平均速度U運動,且U≈k.表明反向移動車輛形成一個緩慢移動的瓶頸,其速度與行人擁堵傳播速度相當,參考圖4(d).當ρ>ρ2時,平均車速逐漸減小,直到完全停止.

圖4給出了典型密度下的行人-車輛時空分布圖.當密度較小時,行人大多分布在道路兩側,見圖4(a)和圖4(b),當ρ?1時,平均車速V≈Vmax.當密度較大時,人車同向與反向兩種情況差異較大:當人車同向時,人群在通道內分布比較均勻,由于車輛對于行人的排斥作用,車輛前方的行人密度略低,見圖4(c),當ρ>ρ1時,平均車速V≈1/ρ?1;而人車反向時,圖4(d)可分為兩個區域,一個是車輛下游的高密度行人擁堵區域,車輛難以向前移動,因此v≈0,U≈0,另一個是車輛上游的低密度行人暢行區域,其中U≈1.由此可知人車反向時車輛所造成的瓶頸效應十分明顯,而同向運動的車輛則不會形成明顯的瓶頸,這也是兩種情況下人群運動基本圖在ρ16ρ6ρ2有顯著差異的根本原因.

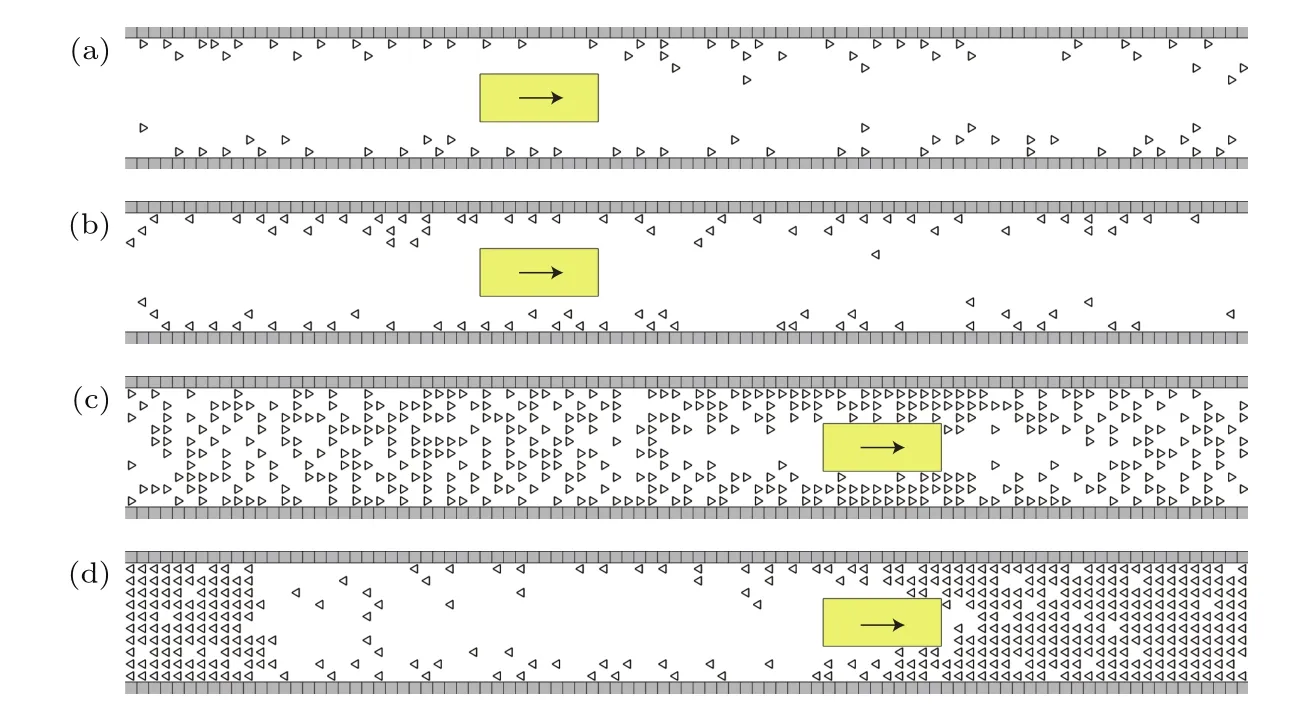
圖4 典型密度下的人車空間分布(L=100,Vmax=5,w=4,τ=3) (a)人車同向,ρ=0.1;(b)人車反向,ρ=0.1;(c)人車同向,ρ=0.5;(d)人車反向,ρ=0.5Fig.4.Spatial distribution of pedestrians and vehicle at typical densities,where L=100,Vmax=5,w=4,τ=3:(a)Case 1,ρ=0.1;(b)Case 2,ρ=0.1;(c)Case 1,ρ=0.5;(d)Case 2,ρ=0.5.

為了更全面了解車輛的運動,下面計算不同行人密度下的短時平均車速時間序列,即每60個時間步長計算一次車速的平均值:

圖5為計算得到的典型密度下短時平均車速的時間序列.

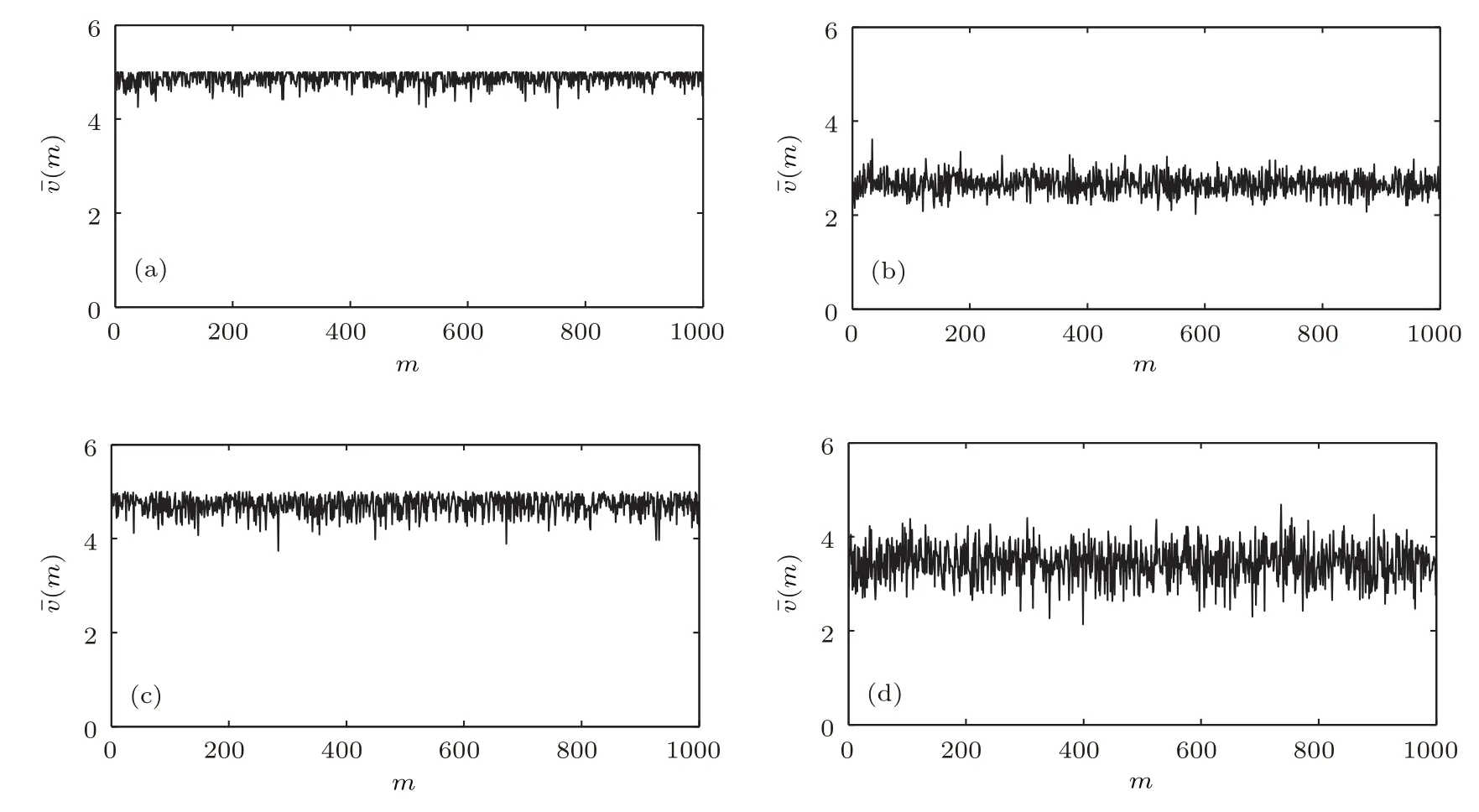
圖5 典型密度下短時平均車速的時間序列 (a)人車同向,ρ=0.1,std=0.142;(b)人車同向,ρ=0.4,std=0.214;(c)人車反向,ρ=0.1,std=0.203;(d)人車反向,ρ=0.2,std=0.382Fig.5.Time series of short time average speed of the vehicle at typical densities:(a)Case 1,ρ=0.1,std=0.142;(b)Case 1,ρ=0.4,std=0.214;(c)Case 2,ρ=0.1,std=0.203;(d)Case 2,ρ=0.2,std=0.382.

從圖5可見,隨著行人密度的增加,短時平均車速減少,同時速度的脈動增大,即標準偏差值(std)增大.當ρ<ρ1時,行人密度相同時,人車反向情況下的短時平均車速下降更快,且有更大的脈動值,表明人車反向時車輛運動更不穩定.

3.3 預判時間的影響

下面研究行人預判時間τ對人車相互作用的影響,結果如圖6所示.當τ較大時,表示行人較為謹慎,反之則表示行人較為冒險.當人車同向時,行人預判時間的長短對于行人基本圖沒有明顯的影響.這是因為當行人密度較小時,行人趨向于沿通道兩側行走,因此預判時間的影響并不明顯,而當行人密度較大時,處于車輛影響區的行人會向兩側運動,由于道路兩側空間有限,在車輛前方容易出現人群堆積而阻擋車輛運動,此時車輛也只能跟著同向運動的行人緩慢向前走.在現實交通中,只要行人密度足夠大,行人通常也不太關注后面的車輛,因為車輛總會盡量避免發生與行人的碰擦.

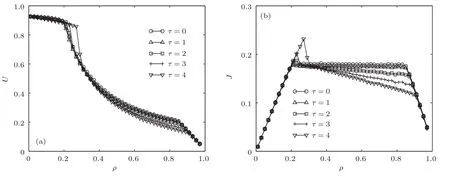
圖6 人車反向運動時考慮不同預判時間的行人基本圖 (a)速度-密度曲線;(b)流量-密度曲線Fig.6.Fundamental diagrams for pedestrian in Case 2 with different anticipation times:(a)Average speed of pedestrians against pedestrian density;(b)flux of pedestrians against pedestrian density.

圖7 不同預判時間時兩種情況下平均車速隨行人密度的變化 (a)τ=0;(b)τ=1Fig.7.Average speed of the vehicle against pedestrian density with different anticipation times:(a)τ=0;(b)τ=1.

圖8 典型密度下的人車空間分布,其中L=100,Vmax=5,w=4,τ=0,ρ=0.04 (a)人車同向;(b)人車反向Fig.8.Spatial distribution of pedestrians and vehicle at typical densities,where L=100,Vmax=5,w=4,τ=0,ρ=0.04:(a)Case 1;(b)Case 2.

從圖6可以看出預判時間對人車反向運動的行人基本圖有一定的影響.隨著τ的增加,臨界密度ρ1和ρ2都有所增加.即在ρ1附近行人平均速度和流量有所提高,當τ=4時更加明顯.當ρ>ρ1時,由于車輛前方出現了局部擁堵,此時采取提前避讓等措施將在一定程度上加劇擁堵程度,因此反而會導致行人平均速度減小、流量明顯下降.由圖6(b)可見,當ρ1<ρ<ρ2時,流量-密度曲線呈線性變化趨勢,其斜率k6 0.τ越大,k越小,表明移動瓶頸向上游移動的速度越大,即考慮行人預判時間,有助于車輛的運動.當τ=0時,可以觀察到一個水平的流量平臺,表明不考慮行人預判時間,車輛將很難前進,會形成一個靜止的瓶頸.

下面研究行人預判時間對車輛運動的影響.如果不考慮預判時間,平均車速隨行人密度的變化如圖7(a)所示,可以看出,當行人密度很小時,人車反向時的車速比同向時還大.這表明當密度很小時,不考慮行人的預判時間,車輛逆行時更容易獲得較高的速度.圖8為典型密度下的人車空間分布,可以看出,在人車同向時,行人隨機分布在通道內,部分通道中間的行人會阻礙車輛的運行(如果考慮預判時間,行人會在車輛到達前提前避讓,對車輛的阻礙就會明顯減少);在人車反向時,即使不考慮行人預判時間,車輛前方的背景場也會驅使行人靠邊行走,減少對車輛的阻擋,因此車速反而較高.而當行人密度進一步增大,逆行車輛造成的局部擁堵會導致車速顯著降低.與此對比,與行人同向的車輛可以跟隨人群前行,所以車速反而會更快一些.如果考慮行人的預判時間,如圖7(b)所示,可以看出,人車同向時的車速始終大于人車反向時的車速.隨著τ的增加,在同一密度下的車速都有一定的提高.這說明無論對于人車同向還是反向,更多的預判時間均有助于提高車輛的運行速度.

3.4 車輛限速的影響

圖9給出了人車反向運動時的行人流基本圖.可見當行人密度較大時,車輛限速對于行人的平均速度和流量幾乎沒有影響,這是可以預期的結果.無論車輛限速多大,一旦車輛前方發生行人擁堵,車輛只能低速緩行.當行人密度較低而車輛限速較大(Vmax=15,20)時,反而導致行人平均速度略有下降,如圖9(a)所示.這是因為行人密度低時高速運動車輛的影響范圍很大,減少了行人的實際運動空間,因此造成人群運動速度的降低.如果采用更大的通道長度,這種效應將會減弱.對于人車同向的情況,其基本圖也呈現類似的性質.由圖9(b)可見車輛限速對ρ16ρ6ρ2之間線性流量-密度曲線的斜率基本沒有影響.

圖10給出了不同車輛限速下平均車速隨行人密度的變化.人車同向時,當Vmax=1時,平均車速緩慢下降,而當Vmax>1時,平均車速下降較快.人車反向時,平均車速很快下降到很低的平均速度,當ρ>ρ1時,U≈0.064,但臨界密度都未發生明顯的改變.

圖11給出了典型密度下短時平均車速的時間序列,可以看出,當Vmax較大且ρ<ρ1時,無論是人車同向還是反向運動時,短時平均車速的脈動均明顯增大,表明車輛運動出現嚴重的時停時走現象;當ρ>ρ1時,與圖5相比,短時平均車速的脈動也有所增加.總體而言,當人車混行時,應該采取較小的車輛限速,或車輛應該緩行.如果車輛盡可能以較高速度運行,往往導致車速變化劇烈,更容易發生擁堵.

3.5 車輛寬度的影響

下面考慮車輛寬度對人車運動的影響.當人車同向時,車輛寬度對行人的平均速度和流量幾乎沒有影響.這是因為在同向運動時,車輛可以視為以較快速度運動的一群人,當遇到前方慢速運動的人群,也只能減速跟隨,更大或更小的車輛寬度都不會產生明顯影響.

圖9 人車反向時不同車輛限速下的行人基本圖 (a)速度-密度曲線;(b)流量-密度曲線Fig.9.Fundamental diagrams for pedestrian in Case 2 with different speed limits:(a)Average speed of pedestrians against pedestrian density;(b)flux of pedestrians against pedestrian density.

圖10 不同車輛限速時平均車速隨行人密度變化曲線 (a)Vmax=1;(b)Vmax=10Fig.10.Average speed of the vehicle against pedestrian density with different speed limits:(a)Vmax=1;(b)Vmax=10.

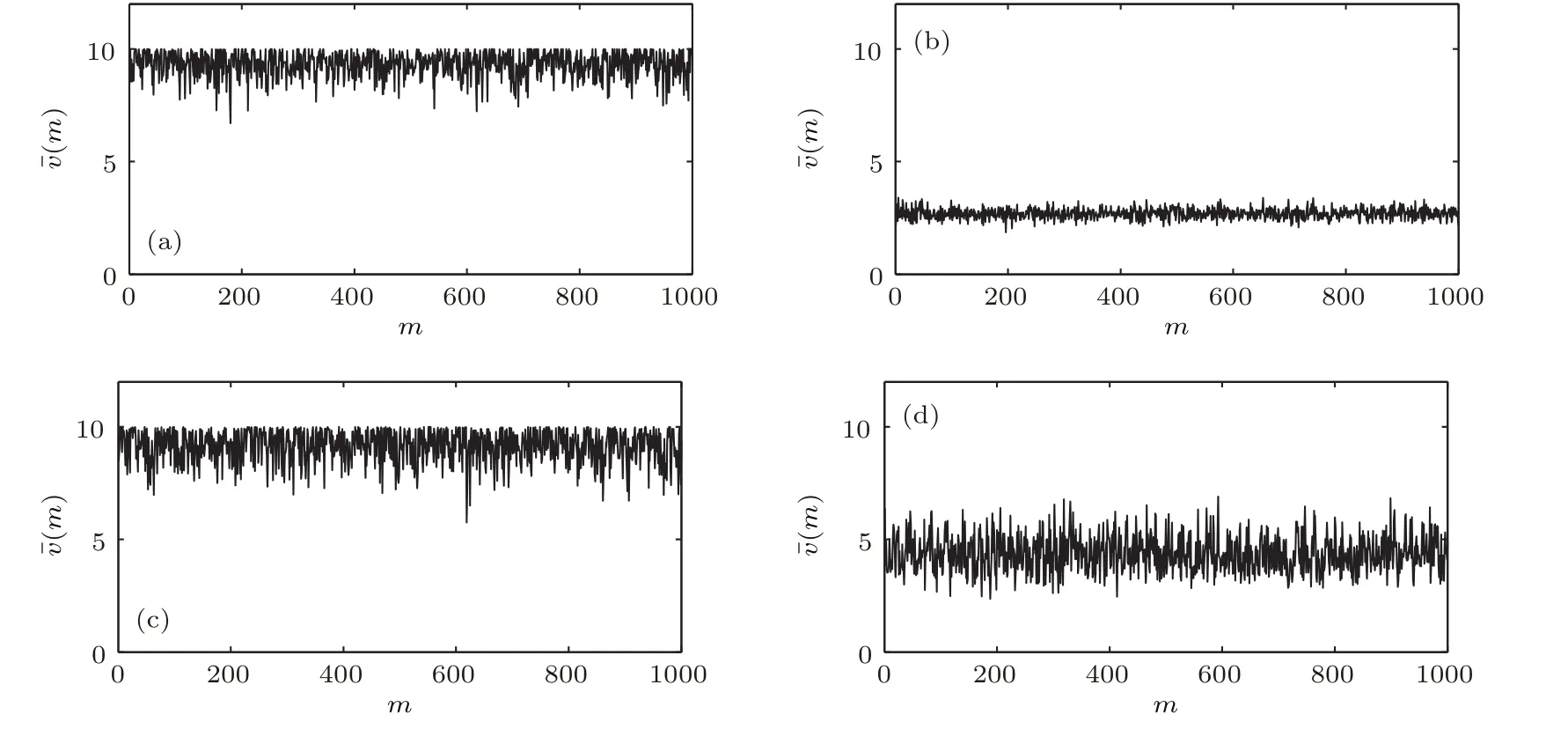
圖11 典型密度下短時平均車速的時間序列(Vmax=10) (a)人車同向,ρ=0.1,std=0.573;(b)人車同向,ρ=0.4,std=0.237;(c)人車反向,ρ=0.1,std=0.725;(d)人車反向,ρ=0.2,std=0.807Fig.11.Time series of short time average speed of the vehicle at typical densities(Vmax=10):(a)Case 1,ρ=0.1,std=0.573;(b)Case 1,ρ=0.4,std=0.237;(c)Case 2,ρ=0.1,std=0.725;(d)Case 2,ρ=0.2,std=0.807.

圖12 人車反向運動時不同車輛寬度下的行人基本圖 (a)速度-密度曲線;(b)流量-密度曲線Fig.12.Fundamental diagrams for pedestrian in Case 2 with different vehicle width:(a)Average speed of pedestrians against pedestrian density;(b)flux of pedestrians against pedestrian density.

與人車同向相比,車輛寬度對于人車反向運動的人群有顯著的影響,如圖12所示.可以看出,臨界密度ρ1發生了顯著變化.車輛寬度越小,ρ1越大,這與日常經驗是相符的.車輛寬度越小,由車輛產生的瓶頸效果就越弱,相應的行人流量也會越大,發生擁堵的臨界密度也會更高.在很高行人密度下,這種效果就變得不明顯,因此ρ2只是略微增大.

從圖13可以看出車輛寬度對平均車速的影響.在同樣的行人密度下,車輛寬度越小,平均車速越大.平均車速和行人運動情況密切相關.隨著行人臨界密度的變化,平均車速也同步變化.車輛寬度越小,車輛開始低速運動的臨界密度ρ1越大,相應的速度值也更大,這也體現在圖12(b)中,即ρ16ρ6ρ2時流量隨密度線性下降的斜率發生變化.

圖14給出了不同車輛寬度時的人車空間分布.可以看出,當車輛寬度較小時,即使在很高密度下,仍有可能向前運動,如圖14(b)所示.而當車輛寬度較大時,即使密度較低,由于車輛較寬,在車輛前方形成更為致密的擁堵區,雖然行人仍然可以通過瓶頸,但是車輛前方有源源不斷的行人補充,始終阻擋車輛的運動,形成一個固定的瓶頸,如圖14(d)所示.

進一步研究不同寬度車輛的平均速度時間序列.對于w=2的情形,當車輛處于運動狀態時(ρ<ρ1),人車同向時的平均車速要超過人車反向運動時的平均車速,且速度脈動更小.當人車同向時,車輛速度脈動隨著行人密度的增加而增大,表明時停時走現象越來越頻繁.當行人密度很高時,車輛速度脈動則會減小.對于人車反向運動的情況,當ρ=0.4時,正好位于臨界點ρ1附近,會出現車輛不同狀態的切換,如圖15(b)所示,且各種狀態都可以維持相當長的時間.由于車輛狀態的隨機切換,導致出現很高的速度脈動.

圖13 不同車輛寬度時平均車速隨行人密度的變化 (a)w=2;(b)w=6Fig.13.Average speed of the vehicle against pedestrian density with different vehicle width:(a)w=2;(b)w=6.

圖14 人車空間分布圖,其中L=100,Vmax=5,τ=3 (a)人車同向,w=2,ρ=0.6;(b)人車反向,w=2,ρ=0.6;(c)人車同向,w=6,ρ=0.4;(d)人車反向,w=6,ρ=0.4Fig.14.Spatial distribution of pedestrians and vehicle,where L=100,Vmax=5,τ=3:(a)Case 1,w=2,ρ=0.6;(b)Case 2,w=2,ρ=0.6;(c)Case 1,w=6,ρ=0.4;(d)Case 2,w=6,ρ=0.4.

圖15 人車反向時典型密度下短時平均車速時間序列(w=2) (a)ρ=0.3,std=0.357;(b)ρ=0.4,std=0.733Fig.15.In Case 2,time series of short time average speed of the vehicle at typical densities(w=2):(a)ρ=0.3,std=0.357;(b)ρ=0.4,std=0.733.

4 結 論

行人和車輛組成的混合交通流會呈現出單一交通流所不具有的特性.本文研究通道中車輛與行人同向或反向運動時人車相互作用.車輛運動的描述采用細化的確定性NaSch模型,而行人流則采用考慮背景場的格子氣模型.車輛及其影響區被視為一種可移動的障礙物,同時車輛影響區的大小依賴于車速以及行人的預判時間,因此它所形成的背景場是動態變化的.通過數值模擬,可以得到典型參數下的行人流基本圖以及平均車速隨行人密度的變化曲線.從人車反向運動時的行人基本圖發現存在兩個臨界密度ρ1和ρ2,當ρ16ρ6ρ2時,流量-密度曲線呈線性分布,其斜率是行人流擁堵向上游傳播的速度,也可以表征車輛所形成的移動瓶頸的速度.當ρ<ρ1和ρ>ρ2時,人車同向和反向的基本圖接近.當人車同向時,車輛則不會導致明顯的瓶頸效應.進一步考察了行人預判時間、車輛的限速以及寬度對人車混合交通流的影響.對于人車同向的情況,這三個參數的影響都不明顯.對于人車反向的情況,車輛寬度的影響最大,行人預判時間次之,而車輛限速的影響最小.當車輛寬度較小時,即使在很高密度下,車輛仍可以前行.而更多的行人預判時間也有助于車輛的運動.人車空間分布和短時平均車速則給出更多人車運動的直觀信息,進一步驗證了定量的模擬結果.本文的結果對于大型活動散場時或隧道內發生事故時的人群疏散有一定的參考價值.

本文對通道中相互作用的行人和車流的研究并重,但僅研究了比較簡單的情況.現實交通中大多會出現雙向行人流與車輛混行的情況,此外還要從實際交通觀測中提取行人和車輛的相互作用的定量信息,并以此作為完善模型的基礎,這些都是值得繼續研究的問題.