252Cf自發裂變中子發射率符合測量的回歸分析?

李永明 王亮 陳想林 阮念壽 趙德山

(中國工程物理研究院材料研究所,綿陽 621907)

(2018年5月31日收到;2018年10月15日收到修改稿)

252Cf同位素源具有標準的自發裂變中子能譜,但由于其半衰期較短,應用中常需要對源強進行標定修正.隨著源年齡增加,來自源中250Cf和248Cm自發裂變的影響愈加凸顯,不能簡單按252Cf的衰變規律計算源中子發射率,而通過錳浴活化的間接測量方法周期較長,且在源強低于104n/s時誤差較大.最近,基于中子多重性計數的源強絕對測量算法已得到驗證.本文進一步從點模型假設的測量方程出發,在將符合計數率與總中子計數率關聯的基礎上,分別對符合計數率隨源位置、符合門寬的變化關系進行回歸分析,提取變化過程的特征系數,建立了兩種避規效率變化的252Cf中子發射率測量方法,并基于JCC-51型中子符合測量裝置開展實驗驗證.結果表明:兩種回歸分析方法的測量值均與標稱值的修正結果在2%的偏差范圍內一致;反推求得裝置中軸線上的探測效率也與基于MCNPX程序的蒙特卡羅模擬計算值相符.研究結果可為活度信息不明的252Cf源強標定及符合測量裝置的效率刻度提供便攜準確的實驗方法.

1 引 言

252Cf源的自發裂變中子能譜已被推薦為國際ISO標準譜[1],廣泛應用于中子探測器的效率刻度[2?4]、中子劑量儀器的標定[5,6]、核材料中易裂變核素含量的激發分析[7,8]等科研工作.但由于其半衰期僅有2.645年[9],且隨著源年齡增加,來自初始250Cf和其α衰變產物248Cm的自發裂變影響愈加凸顯[10,11],不能簡單地只按照252Cf的衰變規律計算源中子發射率,使用前常需要對源強進行標定修正.

基于55Mn(n,γ)56Mn反應的錳浴法[12]可間接測量源中子發射率,但為滿足較好的統計精度,一般要求源強不低于104n/s且需輻照MnSO4溶液達8 h以上[13].而目前國內具備該類基準設備的單位有限,預約標定將涉及源運輸的輻射安保審批,周期較長且費用較大,因此發展更加便攜、更大適用動態范圍的測量方法具有現實意義.

2013年,Croft和Henzlov[14]基于中子多重符合測量原理,建立了點模型假設條件下源強與總中子計數率S、符合計數率D、三重符合計數率T的四種相互關系,經由121根3He正比計數管組成的高效率中子多重符合測量裝置實驗驗證,測量量分別為S-D,S-T,D-T,S-D-T的求解精度都在2%以內,其中S-D方程的誤差最小,其他方法主要受T影響有略大的統計漲落.2014年,國內陳利高等[15]開展了該類測量算法的簡化研究,結合中子在系統內的衰減時間行為先求探測效率,再反推源強;并采用由32根3He正比計數管組成的裝置對5個不同活度的252Cf鍍膜源進行測量,結果與修正標稱值的最大相對偏差為1.41%.上述兩個工作都是在對系統進行參數優化后,將待測源置于探測器中心開展絕對測量.

若源在測量腔體的不同位置系統探測效率將發生改變,且符合計數率也隨符合門寬的增大而增加.但由于入射中子的平均能量相同,其在裝置靈敏探測區域內的平均衰減時間近似為一個特征常數,以上過程可認為滿足相同的測量方程.另外,近年來數字化分析設備已逐步替代移位寄存分析器用于處理中子響應的脈沖時間序列[16],可實現一次測量后加載不同狀態參數的離線反演.由此可探索更為靈活普適的252Cf源強測量方法.

本文從核材料中子被動符合測量方程出發,在約化探測效率的基礎上,考察不同源測量位置、不同符合門寬對計數率的影響,通過回歸分析提取變化過程的相同特征系數,進而求解252Cf源自發裂變的中子發射率,并開展相關的實驗和蒙特卡羅(MC)模擬驗證工作.

2 理論分析

對基于3He陣列的中子符合測量裝置,在將待測樣品的空間分布認為是點源,且假設(α,n)反應中子與自發裂變中子具有相同的能量分布和探測效率的條件下,核材料自發裂變中子的被動符合測量方程可表達為[17]

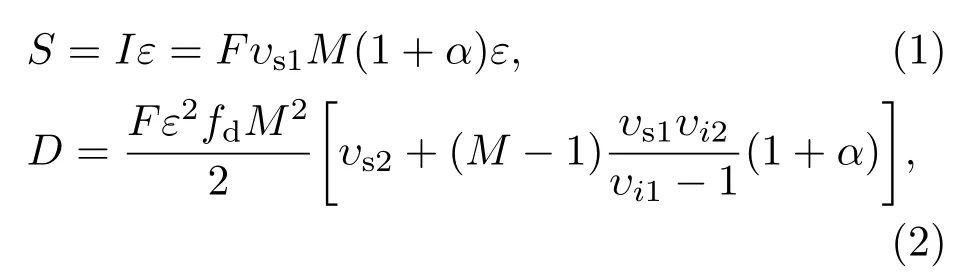
式中,S為總中子計數率,I是核材料的中子發射率,ε是系統平均中子探測效率,F是核材料的自發裂變率,M是中子在待測樣品中的增殖系數,α是核材料(α,n)反應中子與自發裂變中子的比值,D為符合中子計數率,νsj是自發裂變中子多重性分布的j階矩,νij是誘發裂變中子多重性分布的j階矩,fd是雙重符合門寬的利用率:

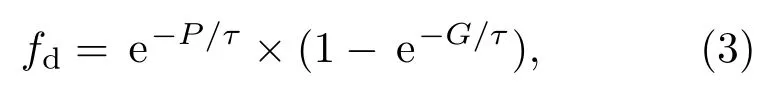
其中,P為預延遲時間,G為符合門寬,τ為中子在裝置中的平均衰減時間常數.

從(1)和(2)式可知,系統探測效率的改變將對D值和S值均產生影響,由此經數學變換可約掉效率,即把符合計數率D由總中子計數率S進行展開:

對不銹鋼封焊的小體積252Cf點源,源材料與18O,13C等核素發生(α,n)反應以及誘發裂變等中子增值因素可忽略不計,可取α=0,M=1,則(4)式進一步簡化為

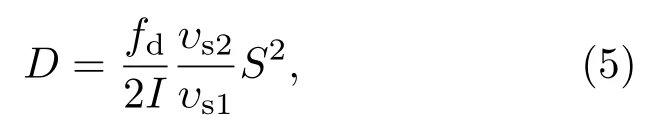
其中,自發裂變中子多重性分布的一階矩和二階矩分別為υs1=3.757;υs2=11.962[17].

2.1 不同符合門寬的源強回歸分析

由(3)和(5)式可知,在測量位置及預延遲固定的情況下,系統fd值和符合計數率均隨著符合門寬的增大而增加,但過程中總中子計數率S不受影響,可認為是個不變量,此時(5)式可進一步簡化為線性關系.設K1為D隨fd的變化斜率,可由最小二乘擬合的回歸分析求出,則252Cf源的中子發射率可表達為

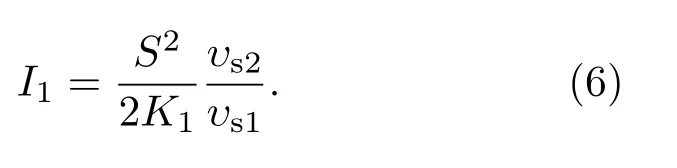
2.2 不同源位置的源強回歸分析

在系統預延遲時間、符合門寬固定,即fd值為常數的情況下,隨著源在測量系統的位置不同,符合計數率隨總中子計數率呈拋物線的變化規律.設K2為D隨S2變化的斜率,可由最小二乘擬合的回歸分析求出,則252Cf源的中子發射率表達為

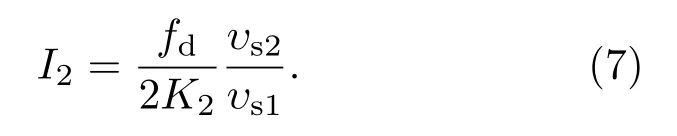
3 實驗測量

本文基于JCC-51型中子多重符合測量裝置[18]開展驗證工作,系統組成及原理流程如圖1所示.該裝置由42根長度為50 cm、氣壓為4 atm(1 atm=1.01325×105Pa)的3He正比計數管分兩環內嵌于高密度聚乙烯組成,測量腔體內徑為22.9 cm、外徑為47.8 cm.探測器工作高壓為+1680 V,前置放大器的輸出信號由數字化分析器MCA527[19]獲取,對中子響應的脈沖序列按照列表模式(list mode)進行標記和存儲.可統計出中子在測量裝置內的符合計數隨時間的衰減分布曲線;加載預延遲時間、符合門寬、延遲時間等參數進行離線反演,可得到總中子計數率、符合計數率和長延遲后的偶然符合計數率,將符合計數率減去偶然符合計數率便得到真符合計數率;考慮死時間修正后可獲得源中子在探測器內的多重性分布.待測的小體積252Cf中子源由美國橡樹嶺國家實驗室生產封裝,活性區直徑和高度均為1.57 mm,2003年11月25日出廠時總活度為4.255×105Bq,其中250Cf占總活度的3.64%,252Cf占總活度的96.31%.

根據裝置說明,固化預延遲時間為4.5μs,延遲時間為1000μs.另外還需對符合門寬進行優化選取,設置過小則符合計數率太低而失去統計意義,過大則偶然符合計數較多,導致真符合計數將是大數減大數的結果.這里先將源置于系統中心,重復3次300 s的測量,將符合門寬從16μs到160μs依次步進調節進行數據反演,步長為16μs,考察不同門寬及其利用率對符合計數的影響.隨后固定一個優化符合門寬,將源沿著探測器中心軸向從距頂部5.0 cm的位置向底部平移,每次步進5.0 cm后重復3次300 s測量,考察不同探測效率下符合計數率D和總中子計數S的變化關系.

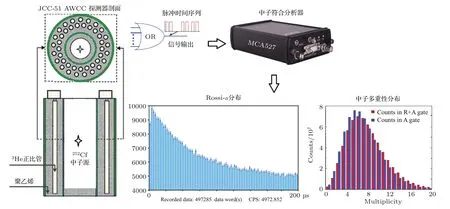
圖1 實驗系統及設置Fig.1.Experimental system and set-up.

4 結果與討論

具有時間關聯特性的源自發裂變中子在裝置中被聚乙烯慢化,以其中一個中子被3He俘獲形成的脈沖作為符合觸發信號,系統在之后t時刻相鄰dt間隔內測到中子數N(t)的分布如圖2所示,滿足指數衰減的Rossi-α分布規律[17]:

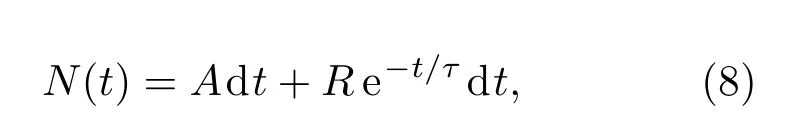
式中A為隨機符合計數率,R為真符合相關的計數率.取dt=1μs,可擬合出中子在裝置中的平均衰減時間常數τ=51.887μs±0.27μs,按(3)式可近一步求出不同條件對應的符合門寬利用率fd.由于預延遲時間P與符合門寬G是精確給定的反演參數,可忽略其不確定性,則fd的標準誤差可由下式求出:

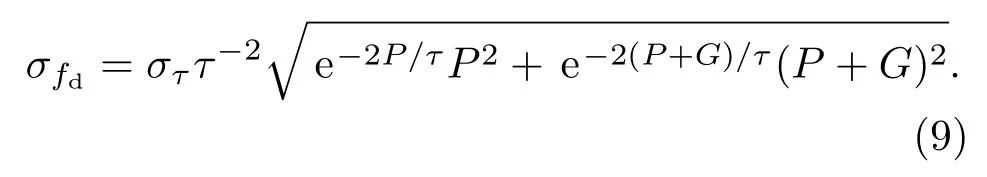
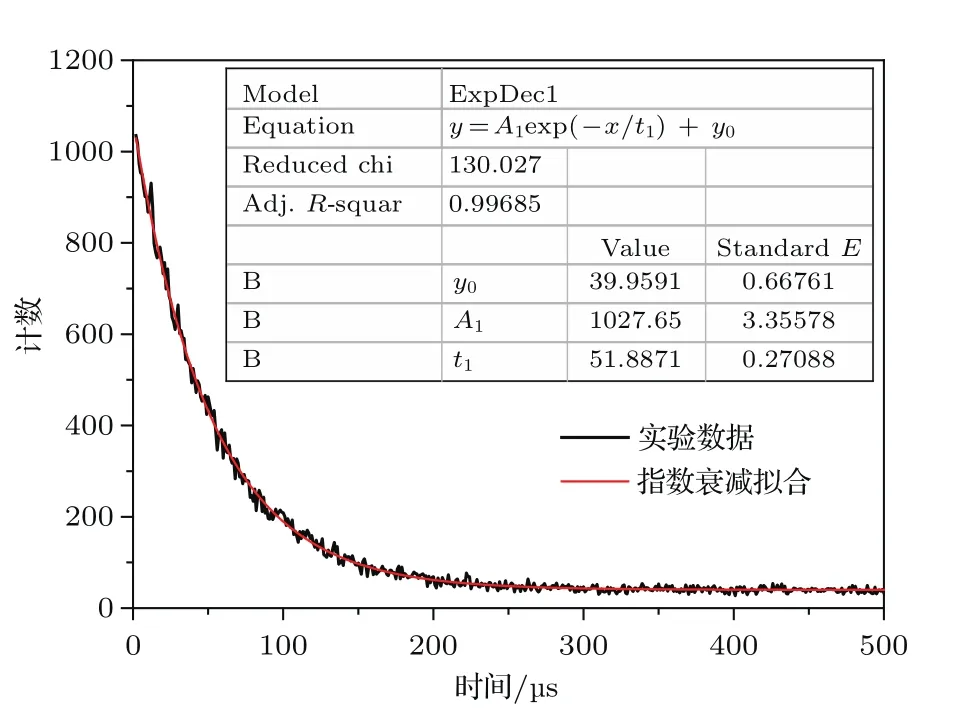
圖2 252Cf源位于裝置中心的中子Rossi-α分布Fig.2.Neutron Rossi-α distribution as252Cf source in the central of counter.

當源置于探測裝置中心,反演得到如圖3(a)所示的符合計數率D隨符合門寬利用率fd的變化趨勢,兩者近似滿足線性關系,在測量時間tm內,總中子計數率S不變,其和D的標準誤差分別為

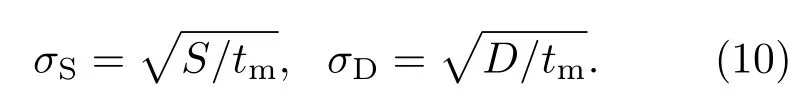
由于系統穩定性較好,在300 s內測量到足夠的統計計數,σS和σD值相對較小,對D-fd關系進行帶誤差的最小二乘擬合,可得斜率K1=176.133±0.090,按(6)式求得源中子發射率I1,其對應的標準誤差為

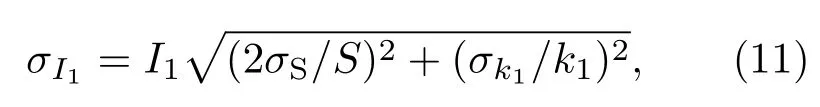
結果為I1=(1202.1±7.3)n/s.

將符合門寬設定為64μs,反演252Cf源置于腔體中軸線不同位置的符合計數率隨總中子計數率平方的變化關系,結果如圖3(b)所示,也近似呈線性,對D-S2數據進行帶誤差的最小二乘擬合可得到斜率K2=8.524×10?4±0.029×10?4,進而按(7)式求得源中子發射率為I2,其標準誤差如下式計算:

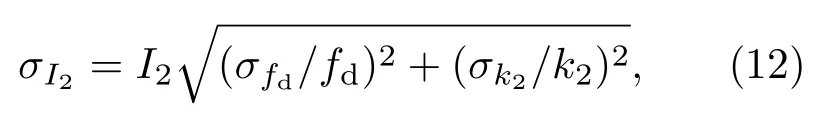
結果為I2=(1213.7±5.5)n/s.

上述實驗于2017年12月27日開展并完成,根據半衰期、自發裂變分支比(T1/2250Cf=13.08年,F250Cf=7.7×10?4;T1/2252Cf=2.645年,F252Cf=3.092×10?2)[9]等參數對源強的出廠標稱值進行修正計算,結果為1225.9 n/s,與兩種回歸分析的測量值在2%的偏差范圍內相符.

求出源中子發射率后,由(1)式可得到裝置中軸線上不同位置的探測效率ε,其標準誤差可由下式求出:

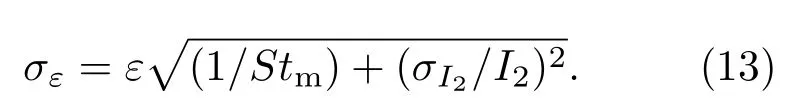
另外,基于MCNPX[20]軟件對測量裝置進行幾何建模和MC計算,跟蹤106個252Cf自發裂變中子,其出射能譜選取為瓦特分布(參數a=1.18 MeV,b=1.03419/MeV),通過統計3He(n,p)3H俘獲反應事件數獲得不同源位的系統探測效率.圖4展示了模擬結果與實驗值的比較情況.當源位于裝置底部時,中子與底座材料發生相互作用的概率增加,S的測量值中包含了部分隨機散射中子的貢獻,導致實驗獲得的效率略高于MC計算值,除此之外的大部分靈敏測量區域內兩者均符合得很好,也進一步驗證了該分析方法的準確性.

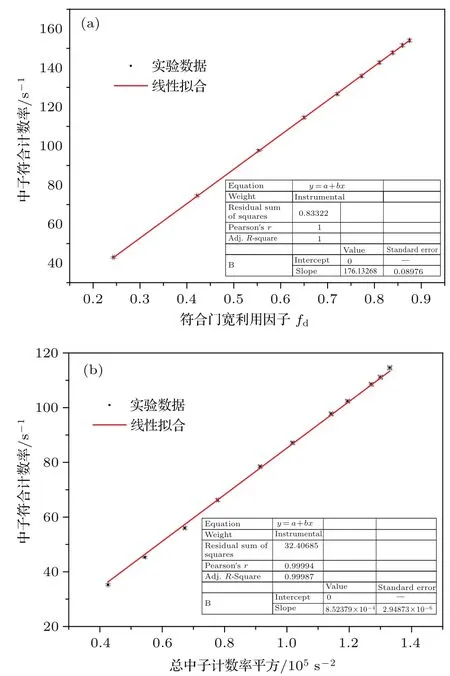
圖3 中子符合計數率的回歸分析 (a)不同的符合門寬;(b)不同的源位置Fig.3. Regression analysis of the neutron coincidence counting rate:(a)Different coincidence gates;(b)source at different positions.

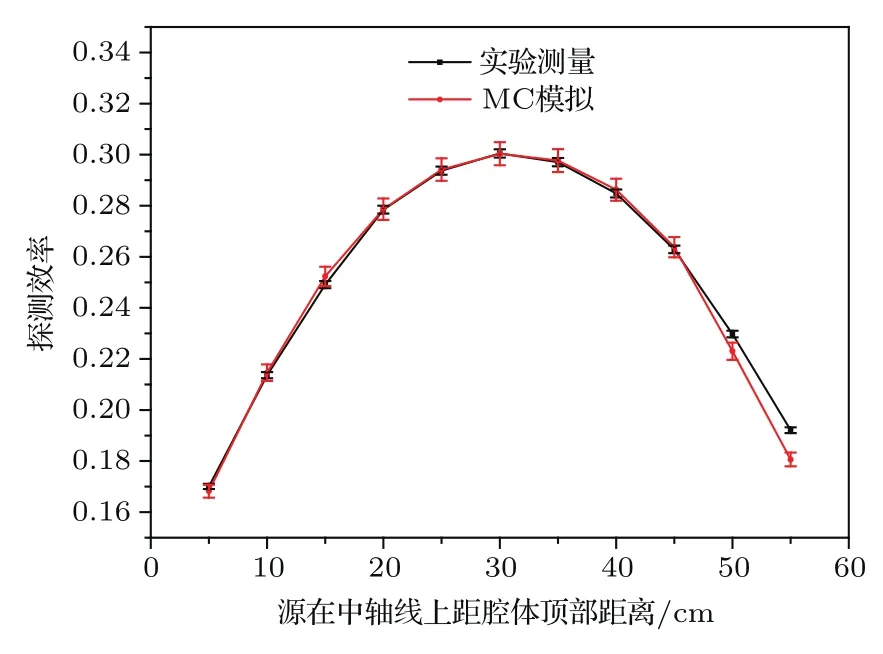
圖4 252Cf源在裝置中軸線不同位置的探測效率Fig.4.Neutron detection efficiency of system as252Cf source at the central axis.

5 結 論

本文建立了兩種不依賴于效率的252Cf源強回歸分析方法.當源固定在測量腔內合適的位置時,通過一次測量后進行多個符合門寬等參數的離線反演,在保障數據的一致性的同時提高了測量的便攜性;當源固定在一優化的符合門寬時,可在靈敏體積內開展較大動態范圍的測量,也有效地降低了對源位的置放精度要求.采用出廠中子強度已知的小體積252Cf源與JCC-51型中子符合測量裝置進行實驗驗證,源中子發射率測量值與標稱值按半衰期修正的結果在2%的誤差內一致,獲得裝置中軸線上不同位置的探測效率也與MCNPX程序的MC模擬結果相符,表明該技術方法是行之有效的.其可應用于新購或未知源強的核對標定;也可在未知源強度的條件下開展符合測量系統的效率刻度,減少了對標準源的依賴.

值得指出的是,隨著源經歷時間的增加,來自250Cf自發裂變的影響將逐步增強[10,11],采用本方法對大于20年以上的老源進行測量時,需要先求解初始250Cf與252Cf的活度比值,再對多重性分布參數進行權重的修正.