基于FRF的螺栓結合部動力學問題的研究

姜濤，董冠華，吳煒，于潔

?

基于FRF的螺栓結合部動力學問題的研究

姜濤1，董冠華2*，吳煒2，于潔3

（1.海軍駐大連426廠軍事代表室，遼寧 大連 116005；2.中國艦船研究設計中心，湖北 武漢 430000；3.大連船舶重工集團有限公司，遼寧 大連 116005）

螺栓聯接是機床結合部的重要形式之一，其動力學特性對機床動態特性影響顯著。從子結構綜合的思想出發，通過FRF法建立了螺栓聯接結合部動力學的理論模型，并基于力學平衡方程和位移兼容方程，推導了結合部動剛度的辨識方程；進而，基于最小二乘法提出了結合部動剛度的等效計算方法；最后，規劃了基于LMS振動測試環境的動力學試驗，測試結果顯示：有限元預測值與試驗實測值之間一致度良好，驗證了方法的可行性。

螺栓；結合部；動力學；參數辨識；FRF

機床結合部提供了機床整機的約60%～80%柔度特性[1-2]和約90%阻尼特性[3]，結合部引起的變形量約占機床總變形量的40%～60%。結合部動力學特性是組合結構系統及整機結構系統除結構幾何邊界、材料屬性之外的重要邊界條件，結合部動力學辨識和建模方法的正確性直接決定所建立模型的預測精度。因此，準確辨識結合部動力學參數是建立整機動力學模型的前提，結合部動力學的研究對機床結構動力學而言具有重要的理論意義。

研究直線導軌結合部動力學特性的主要方法有：基于頻響函數法、模態試驗法、接觸分形法的參數辨識。頻響函數法辨識結合部動力學參數的研究最早由Okubo和Miyazaki[4]提出，且得到了Burdekin[5]、Tsai[6]、Yang[7]等人的進一步拓展，孫偉[8]將之成功應用于導軌結合部動態特性的研究上，試驗效果良好；模態試驗法是以模態參數為目標向量通過不斷迭代辨識結合部參數的方法，孫明楠[9]、米良[10]建立了導軌結合部的動力學模型，搭建了MATLAB- ANSYS聯合仿真的試驗平臺，構建了導軌滑塊結合部的辨識環境；Ninomiya[11]基于分形理論分析了直線導軌結合部與軸承結合部的剛度特性，并提出了通過預緊載荷提高結合部剛度的方法，并進行了試驗驗證。

論文在充分理解子結構綜合思想的基礎上，通過FRF（Frequency response function，頻響函數）建立了螺栓結合部動力學的理論模型，并基于力學平衡方程和位移兼容方程，推導了結合部動剛度的辨識方程；進而，基于最小二乘法提出了結合部動剛度的等效計算方法；最后，規劃了基于LMS振動測試環境的動力學試驗，測試結果顯示：有限元預測值與試驗實測值之間一致度良好，驗證了方法的可行性。

1 結合部動力學基礎

復雜機械結構系統基本可以分為三個系統，由子結構本身組成的子結構系統、結構聯結區域組成的結合部系統、子結構系統和結合部系統共同組成的組合結構系統，如圖1所示。

組合結構動力學系統的輸入輸出關系可表示為：

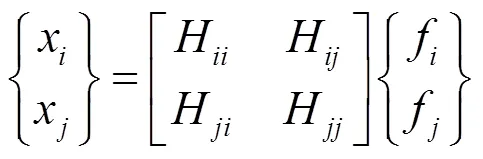
式中，為位置的響應位移；為頻響函數；為激振力。角標為模型中對應坐標位置。

子結構系統的動力學輸入輸出關系可類似表示為：

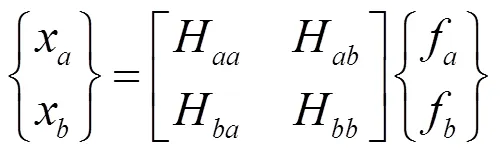
結合部系統的動力學特性可表示為：

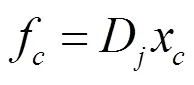
通過力學平衡方程和位移兼容方程，得到：

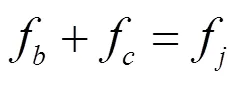
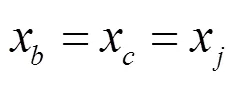
由式（1）～式（5）可以推導得到結合部動力學參數的四個基本辨識方程為：

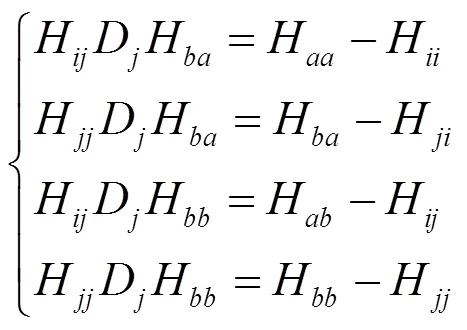
由式（3）及式（6），參考文獻[7]可通過廣義逆矩陣實現動力學參數等效計算：

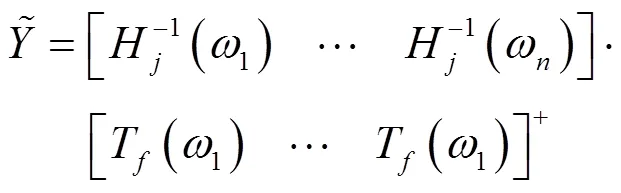
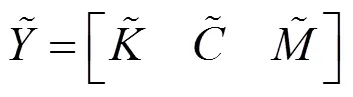
2 試驗驗證

為驗證辨識方法的正確性，通過LMS振動測試環境規劃了動力學試驗。試驗布置了兩個試件，材質分別選用鑄鐵和碳鋼，以模擬機床中導軌與床身之間的接觸邊界，通過力矩扳手將螺旋預緊力矩設置為60 N·m。試驗通過力錘進行激勵，并通過加速度傳感器進行拾振。如圖2～圖5所示。

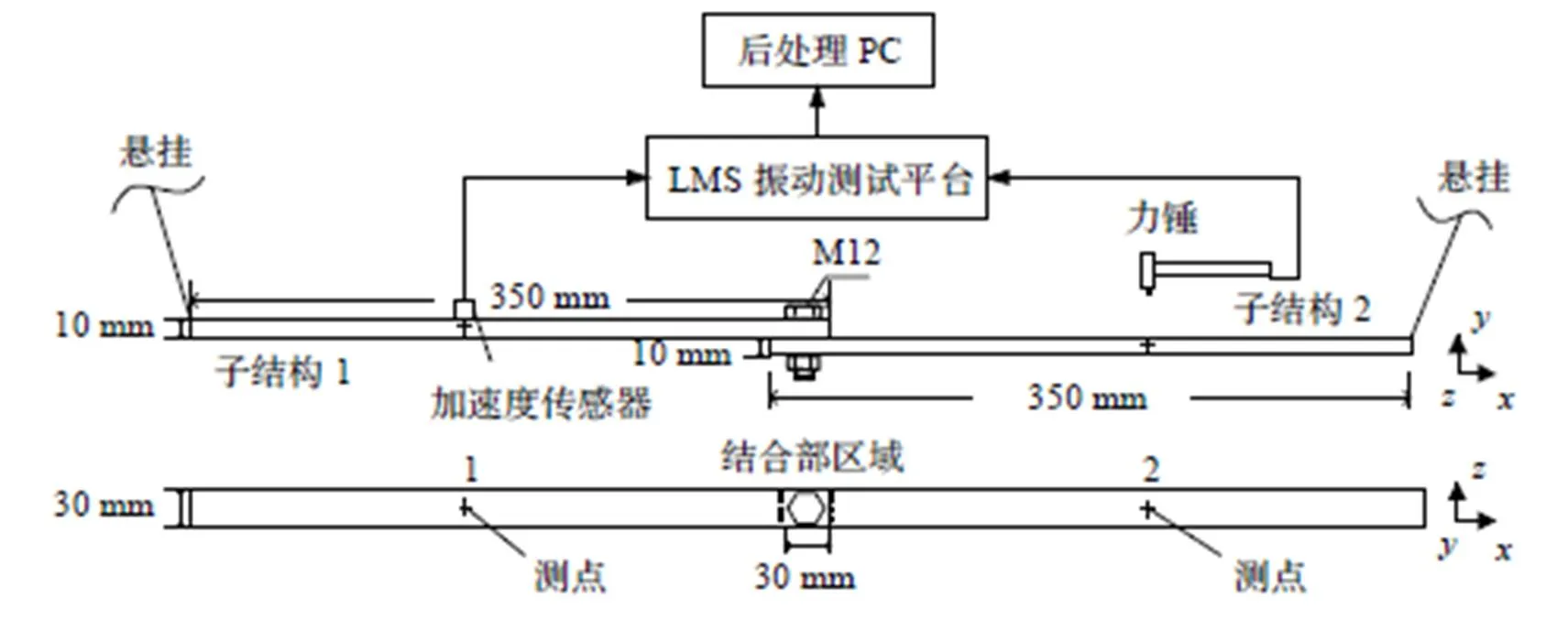
圖2 試驗配置

圖3 試驗現場

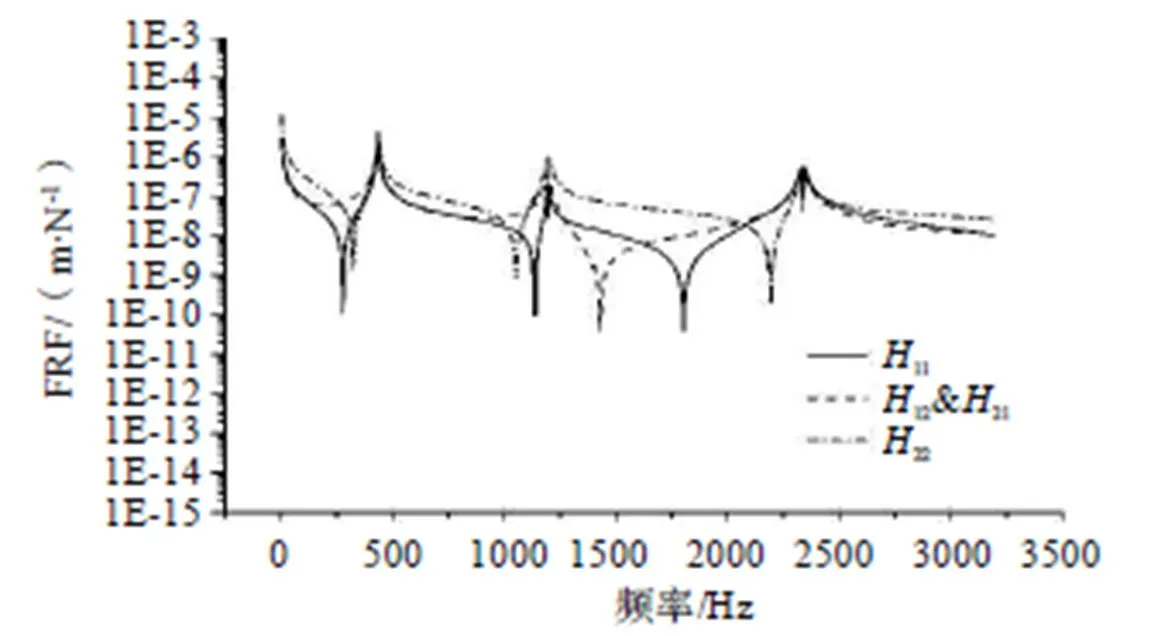
圖4 子結構測試頻響

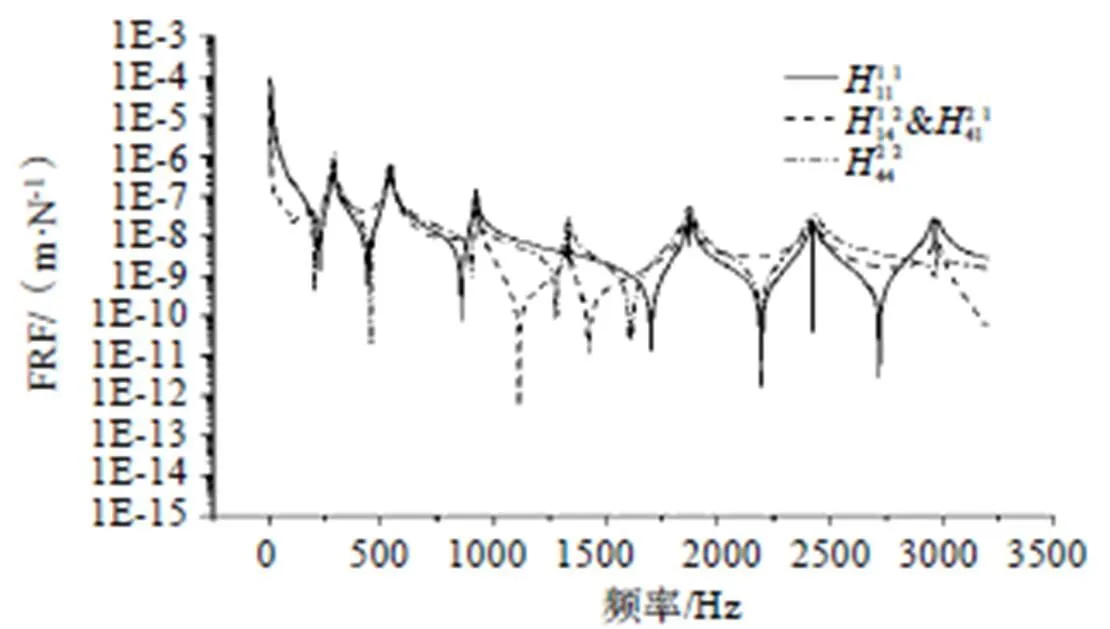
圖5 組合結構頻響

基于測試數據和辨識方程可獲得結合部動力學參數的等效值，將之錄入有限元軟件，建立組合結構系統的動力學模型及其預測結果如圖6、圖7所示。

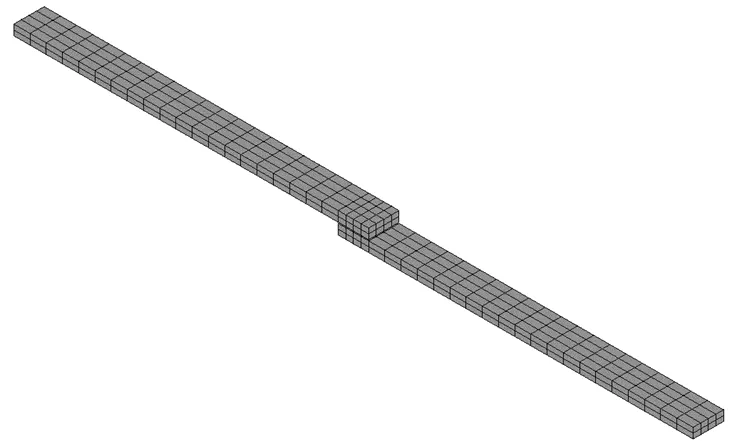
圖6 組合結構系統有限元模型

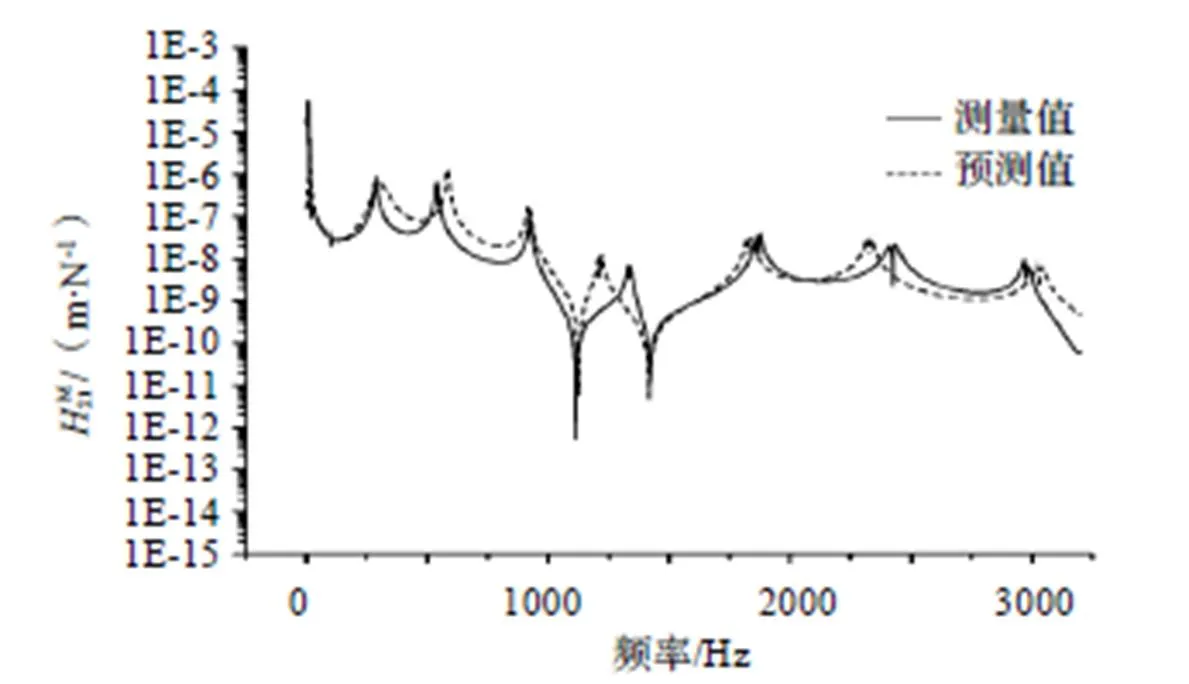
圖7 結果對比圖

3 結論

從子結構綜合思想出發，通過頻響函數建立組合結構動力學的理論模型，模型中充分考慮結合部動力學特性對組合結構動態特性的影響；基于力學、位移邊界推導了結合部動力學參數的四個辨識方程，并給出等效計算方法；動力學試驗值和預測值之間具有良好的一致性，驗證了方法的可行性。

[1]Gaul L，Nitsche R. The Role of Friction in Mechanical Joints[J]. Applied Mechanics Reviews，2001，54（2）：5173-5184.

[2]Vafaei S，Rahnejat H，Aini R. Vibration monitoring of high speed spindles using spectral analysis techniques[J]. International journal of machine tools and manufacture，2002，42（PII S0890-6955(02) 00049-411）：1223-1234.

[3]Burdekin M，Back N，Cowley A. Analysis of the local deformations in machine joints[J]. Archive Journal of Mechanical Engineering Science 1959-1982 (vols 1-23)，1979，21（1）：25-32.

[4]N. Okubo M M. Development of uncoupling technique and its application: Proceeding of International Modal Analysis Conference，Florida，USA，1984[C].

[5]Burdekin M，Back N，Cowley A. Analysis of the local deforma- tions in machine joints[J]. ARCHIVE Journal of Mechanical Engineering Science 1959-1982 (vols 1-23)，1979，21（1）：25-32.

[6]TSAI J S，CHOU Y F. The Identification of Dynamic Characteristics of a Single Bolt Joint[J]. Journal of Sound and Vibration，1988，125（3）：487-502.

[7]YANG K T，PARK Y S. Joint Structural Parameter-Identification using a subset of Frequency-Response Function Measurements[J]. Mechanical Systems and Signal Processing，1993，7（6）：509-530.

[8]孫偉，汪博，聞邦椿. 直線滾動導軌結合部動力學特性測試及參數識別[J]. 東北大學學報（自然科學版），2011（5）：716-719.

[9]孫明楠，米良，干靜，等. 數控機床導軌結合部動態特性參數優化識別方法研究[J]. 四川大學學報（工程科學版），2012（3）：217-223.

[10]米良，殷國富，孫明楠，等. 基于結合部動力學特性的立柱-主軸系統動力學模型研究[J]. 農業機械學報，2011（12）：202-207.

[11]Ninomiya M, Kato S. Analysis of Linear Guide and Ball Screw Stiffness[J]. International Journal of the Japan Society for Precision Engineering，1999，33（3）：173-177.

Research on Dynamics of Bolted Joint Based on FRF

JIANG Tao1，DONG Guanhua2，WU Wei2，YU Jie3

(1.Military Representative Office of the Navy in Dalian 426 Factory, Dalian 116005, China; 2.China Ship Development andDesign Center, Wuhan 430000, China; 3.Dalian Shipbuilding Industry Co., Ltd., Dalian 116005, China )

Bolt connection is one of the important forms of contact surface of machine tool, and its dynamic characteristics have great influence on dynamic characteristics of machine tool. In this paper, the theory model of bolted joint is established based on substructure synthesis method of FRF, and the fundamental formulas are deduced via the mechanical equilibrium equation and the displacement compatibility equation. The equivalent calculation method of the dynamic stiffness is proposed based on the least square method. The dynamic test is planed based on LMS vibration testing platform. The test results show that the predicted value of finite element is in good agreement with the measured value, and the feasibility of the method is verified.

bolt；joint；dynamic；identification；FRF

TG156

A

10.3969/j.issn.1006-0316.2018.12.002

1006－0316 (2018) 12－0004－04

2018－08－13

國家科技支撐計劃項目（2015BAF27B01）；四川省科技計劃項目（2014GZ0125）

姜濤（1985－），男，遼寧營口人，本科，工程師，主要研究方向為船舶動力。

董冠華（1989－），男，山東濰坊人，博士，工程師，主要研究方向為船舶動力。