時間約束下任務關鍵系統的可調度性分析

陳 瑩,邢建春,楊啟亮,,張孝鵬

(1.陸軍工程大學 國防工程學院,南京 210007; 2.南京大學 計算機軟件新技術國家重點實驗室,南京 210093;3.酒泉衛星發射中心,甘肅 酒泉 732750)

0 概述

任務關鍵系統(Mission Critical System,MCS)[1]是指在系統運行過程中不能發生中斷或失效,否則將導致任務執行失敗,造成嚴重的經濟損失或人員傷亡的系統。如何在時間有限的情況下保證現有的關鍵任務持續、及時完成,己成為亟待解決的問題。時間約束下的任務關鍵系統的可運行性分析,也就是確保有限時間約束內能夠完成任務的觸發問題。因此,首先需要研究整個系統中所有活動是否都為可調度的。

在工作流網系統中,如果任何2個變遷之間都不存在潛在的資源沖突,那么稱此工作流模型是可調度的。對于不可調度的活動,結合關鍵任務等級,通過對活動的時間約束進行修正使得工作流模型變成可調度[2]。時間約束下的任務關鍵系統的調度性問題本質上是一個非線性規劃問題[3]。

時間約束下工作流程的建模是其時間性能分析的前提,具有強大時間約束表達能力和數學基礎的時間約束Petri網(Timing Constraint Petri Net,TCPN)在建模方面得到了廣泛應用。然而,TCPN強大的時間約束描述能力也使得可調度性的分析難度大大增加。因此,眾多學者從不同角度對其進行了研究。文獻[1]提出了TCPN的概念,并給出了最基礎的調度驗證的方法,很多學者的研究都基于此方法;文獻[2]提出了基于Petri網的時間約束工作流的可調度性驗證算法;文獻[4]從結構、時間、資源限制3個層面提出多工作流系統的原型,并進一步給出多工作流網下的可調度性驗證算法和修正策略;文獻[5]完善了TCPN的定義,并提出了TCPN時間可調度性判定定理;文獻[6]提出了4種基本工作流組件模型的簡化規則和壓縮推理方法;文獻[7]對文獻[2]的驗證算法進行了改進,使得算法更加簡潔,減小了時間復雜度;文獻[8]提出了擴展的時間約束Petri網(w-TCPN)的定義,并結合w-TCPN的拓撲結構,從模型和實例2個層次給出了w-TCPN可調度的判定定理,并描繪了時間約束的修正策略;文獻[9]提出了一種基于Parsec的并行計算工作流調度算法;文獻[10]進行了基于集群拓撲結構的工作流調度研究;文獻[11]針對軍事網格應用及工作流的特點,給出一種基于網格工作流分割的調度算法;文獻[12]提出了一種基于多QoS目標的工作流任務調度算法;文獻[13]對工作流進行了建模與分析。

近些年有關可調度性分析的研究,大部分都基于TCPN,沒有加入任何新元素,限制了可調度性分析的應用范圍。基于此不足,本文通過引入任務關鍵系統這一元素,在時間約束著色Petri網(Timing Constraint Color Petri Net,TCCP-Net)中,提出一種任務關鍵系統的可調度性靜態分析、動態分析及其修正策略。

1 TCCP-Net語義及相關概念

1.1 關鍵任務等級劃分

任務關鍵系統的時間約束驗證有兩方面要求。一方面,整個工作流過程是在一定時間約束下進行的,文中給出每一個庫所的時間約束最大值,即Vpmax。另一方面,將任務根據不同的重要程度分為不同的等級,文中將其分為2個等級。

定義1關鍵系統中的任務分為關鍵任務和非關鍵任務。其中,關鍵任務是為完成最終任務必須要執行的任務,且每個工作流程中最少要有一個關鍵任務。

1.2 TCCP-Net定義

定義2時間約束著色Petri網(TCCP-Net)。一個時間約束著色Petri網是一個七元組:TCCP-Net=(P,T,F,M0,C,PT,D)。

1)P:描述系統庫所(Place)的有限集合;

2)T:變遷(Transition)的有限集合;

3)F:弧(Arc)的有限集合,滿足F?(P×T∪T×P);

4)M0:初始變量;

5)C:與每個庫所和變遷關聯的色彩集。具體地,庫所pi的色彩集為C(pi)={ai,1,ai,2,…,ai,ui},其中,ui=C(pi),i=1,2,…,n,變遷tj的色彩集為C(tj)={bj,1,bj,2,…,bj,vj},vj=C(tj),j=1,2,…,m;

6)PT是定義在庫所集和變遷集上的整數對PT(pj,tj)=[Vl(pt),Vc(pt)]的集合;

7)D是變遷的執行延遲Vd(t)的集合。

1.3 TCCP-Net中時間參數的形式化定義

圖1為一個TCCP-Net的片段,Vl(pt)、Vc(pt)和Td(t)的單位為時間單元,如天(d)、小時(h)等。

圖1 TCCP-Net片段

結合圖1,將TCCP-Net中庫所和變遷的時間約束條件進行說明,除此之外,為了下文討論方便,此處給出一些其他變量的定義和運算公式。

1)[Vl(p1),Vc(p1)]和[Vl(p2),Vc(p2)]分別為庫所p1和p2上的局部時間約束值,表示庫所中的托肯對后續變遷的使能區間。假設托肯到達庫所p1的時間為V0,則在區間[V0+Vl(p1),V0+Vc(p1)]內變遷t1被使能。

2)[Vl(t1),Vc(t1)]為變遷t1的局部時間約束值,表示t1的可觸發時間。假設變遷t1在V1時刻使能,那么其可觸發時間為[V1+Vl(t1),V1+Vc(t1)]。

3)Vd(t1)表示變遷t1完成觸發所需要的時間延遲。假設變遷t1的觸發時刻為V2,那么完成觸發的時刻為V2+Vd(t1)。

4)[EVl(p),EVc(p)]為庫所p使能的時間區間,此區間是上文中托肯對后續變遷使能區間的交集。

5)[EVl(t),EVc(t)]為變遷t使能的時間區間。

6)[FVl(t),FVc(t)]為變遷t的可觸發時間區間。

7)[FVbegl(t),FVendc(t)]為變遷t觸發的最早開始時刻和最晚結束時刻。其中,FVendc(t)=EVc(p)。

8)Token(pn)j為第n個庫所中第j個托肯到達的時刻,并且每一個庫所托肯的到達時間Token(p)取決于庫所中最后一個托肯的到達時間。

由于變遷完成觸發還需要一定的時間延遲Vd(t),也就是說如果要求變遷能夠成功觸發,需要滿足條件Vc(t)-Vl(t)≥Vd(t)。

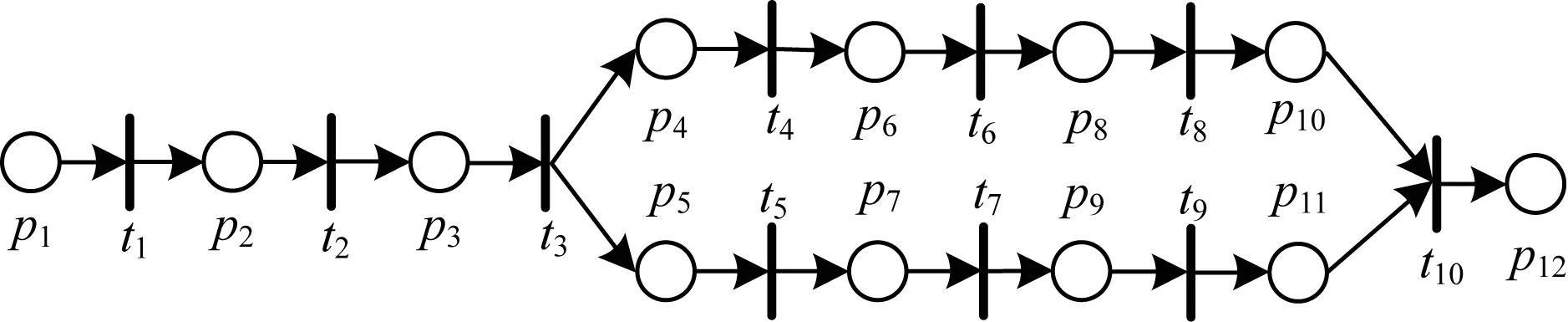
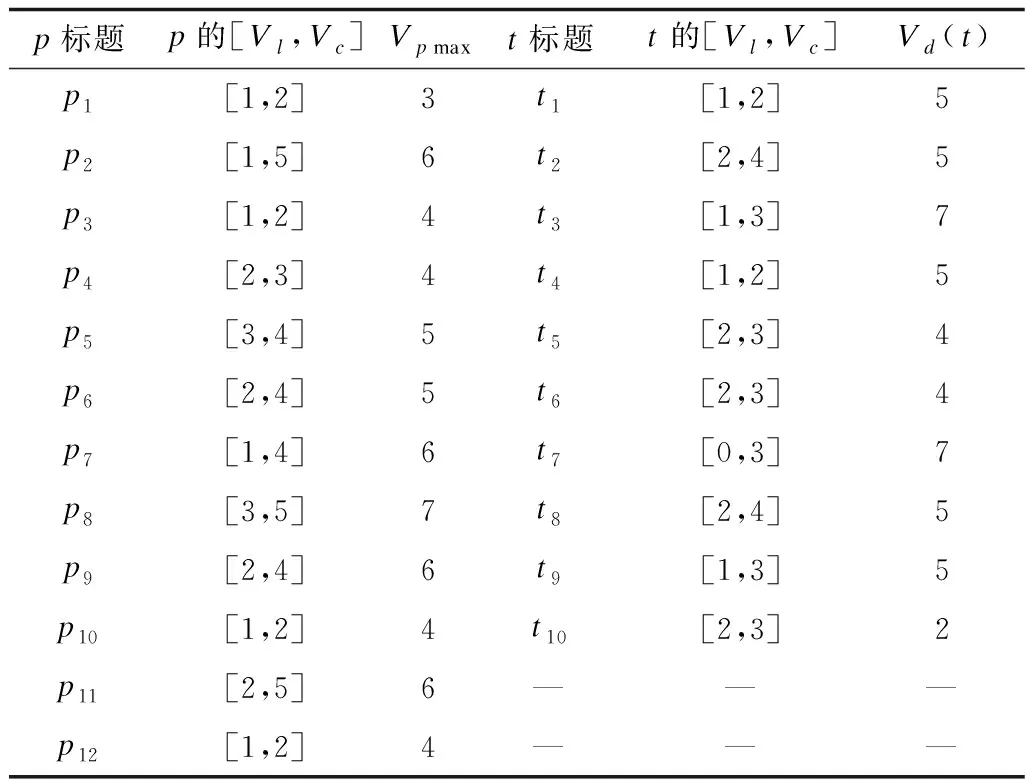
變遷可調度性的驗證問題,歸根結底是驗證變遷觸發結束時刻值與出發開始時刻值之差是否滿足時間延遲的約束。因此,當變遷的最晚觸發結束時刻的值FVendc(t)與最早觸發開始時刻的值FVbegl(t)的差值都不滿足時間延遲Vd(t)的約束,也即FVendc(t)-FVbegl(t)

規則1在TCCP-Net網的某一狀態標識M下,如果變遷t滿足:

FVendc(t)-FVbel(t)≥Vd(t)

(1)

那么變遷t是可調度的。

定義3TCCP-Net網是可調度的,當且僅當網中每一個變遷都是可調度的。

定義4前驅庫所(precursor place)。如果有向弧從p連接到t,那么活動t就稱為p的前驅庫所,即·p。帶有m個托肯的庫所如圖2所示。

圖2 帶有m個托肯的庫所

當只有一個變遷時,若要變遷t進入觸發階段,則需要所有前驅庫所都處于使能階段,也就是說前驅庫所中的所有托肯都必須到達,因此,FVbegl(t)和FVendc(t)的計算公式為:

FVbegl(t)=FVl(t)=EVl(t)+Vl(t)=

min{Token(·p1)m}+Vl(·p)+Vl(t)

(2)

FVendc(t)=EVc(t)=max{Token(·p1)1}+Vc(·p)

(3)

式(2)表示當變遷t處于使能階段時,需要經過Vl(t)時間才能使得變遷t處于最早觸發時間階段,并且變遷t最早使能時間取決于最后一個托肯的到達時間;式(3)表示當庫所處于觸發階段,變遷t處于使能階段時,必須馬上被觸發,否則庫所中的托肯將會丟失,從而導致變遷無法被觸發,并且變遷t最晚使能時間取決于第一個托肯對其使能時間的最大值。

2 時間約束下的CTPN可調度性分析

工作流過程的可調度性分析一般分為靜態分析和動態分析[14]。其中,靜態分析是指不考慮托肯到達庫所的時間,動態分析又稱強可調度性分析,是指需關注不確定因素對工作流過程帶來的影響,其最大的影響因素就是托肯到達庫所的時間。

在實際的工作流過程中,只有資源(托肯)全部到達,活動(變遷)才能夠被觸發,從而使得整個過程得以運行。在分析工作流過程的可調度性時,只有考慮到托肯的到達時間才具有實際意義。因此,文中只對可調度性進行強可調度性分析。

2.1 可調度性分析方法

通過規則1可知,變遷的可調度性取決于變遷和前驅庫所的時間約束。從圖3可以看出,只有并行路徑的庫所需要大于一個的托肯數。換句話說,只有并行路徑存在變遷擁有多個前驅庫所的情況。但根據結構可知,其他路徑是并行路徑的一個特殊情況,因此,只需分析并行路徑中多個前驅庫所的情況即可。

圖3 變遷路徑的基本結構

定理1在TCCP-Net網的某一狀態標識M下,具有n個前驅庫所的變遷強可調度性充要條件為:

min{Token(·pi)1}-max{Token(·pi)m}+

minVc(·p)-maxVl(·p)-Vl(t)≥Vd(t)

(4)

其中,1≤i≤n。

證明

由于:

FVbegl(t)= max{min{Token(·pi)m}+

Vl(·p)}+Vl(t)

其中,1≤i≤n。

FVendc(t)= min{max{Token(·pi)1}+

Vc(·p)}

其中,1≤i≤n,帶入式(1)可得:

min{ max{Token(·pi)1}+Vc(·p)}-

max{min{Token(·pi)m}+

Vl(·p)}+Vl(t)≥Vd(t)

也即:

min{ max{Token(·pi)1}}-

max{min{Token(·pi)m}+minVc(·p)-

maxVl(·p)-Vl(t)≥Vd(t)

其中,1≤i≤n,式(4)得證。

綜上所述,工作流過程的可調度性分析的基本思路為:根據已知時間約束,計算變遷t觸發最早開始時刻FVbegl(t)和最晚結束時刻FVendc(t)的值,然后比較FVendc(t)-FVbegl(t)≥Vd(t)是否成立。若成立,則可判斷t是強可調度的;若不成立,則應對變遷及其前驅庫所的時間約束進行修正,從而使得變遷為強可調度的。

2.2 時間約束修正策略與算法

工作流過程的可調度分析不僅要驗證工作流中的變遷是否可調度,還要對不可調度的變遷進行修正,使得整個工作流網都為可調度的。由式(4)可知,影響變遷可調度性的元素有4種:庫所使能時間上限,庫所使能時間下限,變遷可觸發時間下限和變遷完成觸發所需的時間延遲。其中,時間延遲是固定值,無法進行修改。那么,如果要使得式(4)成立,根據對工作流過程的總的時間約束值Vpmax,可首先減小變遷可觸發時間下限值;若仍不成立且V≤Vpmax,則可減小庫所使能時間下限值并增加庫所使能時間上限值;最后,若式(4)仍不成立且V≥Vpmax,則根據關鍵任務的等級程度對其進行取消執行。假設工作流時間約束為Vpmax,當V≤Vpmax時,具體步驟如下:

步驟1減小Vl(t)的值,如果Vl(t)≥0且式(4)成立,轉入步驟4,否則轉入步驟2。

步驟2減小Vl(·p)的值,如果Vl(·p)≥0且式(4)成立,轉入步驟4,否則轉入步驟3。

步驟3尋找變遷t的直接前驅庫所·p,增加Vc(·p)的值,當式(4)成立,但V(·p)>V(·pmax)時,若活動t為非關鍵任務,則可直接取消執行任務t;若活動t為關鍵任務,則增大Tmax的值,直到式(4)成立。

步驟4結束。

3 案例分析

圖4為某港岸基保障信息系統流程,碼頭一般設置有食品供應中心、供水中心、供電中心、供暖中心等岸基保障設施,所以艦艇靠岸駐泊后,岸基保障部門通過這些保障設施為其補給水、電、氣、食品以及軍械、彈藥等物資[15],其工作流程如圖4所示。其中:p1表示準備提交申請;p2表示準備進行審核;p3表示完成審核,準備部門批準;p4表示完成批準,準備配備食品;p5表示完成批準,準備配備水電;p6表示準備調用貨車;p7表示準備調配保障人員;p8表示食品裝配完畢,待運輸;p9表示水電準備完畢,待配送;p10表示食品輸送完畢,待確認;p11表示水電配送完畢,待確認;p12表示水電配送完畢,待確認;t1表示提交申請;t2表示部門進行審核;t3表示部門批準;t4表示配備需供應的食品;t5表示配備需供應的水電;t6表示將貨車調到食品供應站;t7表示調用保障人員;t8表示用貨車運輸食品;t9表示保障人員進行水電配送;t10表示確認任務完成。

圖4 案例工作流程

案例工作流程時間約束集PT如表1所示,其時間單位為min。

表1 案例工作流程時間約束集

一只艦艇靠岸駐泊后,假設庫所p中有2個托肯,到達庫所的時間區間分別為:Token(p)1=[1,3]和Token(p)2=[2,5],且t4～t9為關鍵任務,t1～t3、t10為非關鍵任務。運用第2節所述的工作流過程,可調度性驗證方法對案例進行驗證的過程如下:

1)對活動t1進行驗證,其最早觸發開始時間值與最晚觸發結束時間值分別為:

FVbegl(t1)= min{Token(·p1)2}+Vl(·p1)+

Vl(t1)=4

FVendc(t1)= max{Token(·p1)1}+

Vc(·p1)=5

由于FVendc(t1)-FVbegl(t1)=1<5,對活動t1的時間約束進行修正:

(1)減小Vl(t1)的值至0,則FVendc(t1)-FVbegl(t1)=2<5,活動仍不可調度約束。此時,活動t1新的時間約束為[0,2]。

(2)減小Vl(·p1)的值至0,則FVendc(t1)-FVbegl(t1)=3<5,活動仍不可調度約束。此時,庫所p1新的時間約束為[0,2]。

(3)若要使得FVendc(t1)-FVbegl(t1)≥5,FVbegl(t1)的最小值為2,那么就需要增加FVendc(t1)的值,由上述分析可知增加Vc(·p1)的值為4時,不等式成立。此時庫所p1新的時間約束為[0,4]。但由已知條件可知,V(p1)max=3,并且活動t1為非關鍵任務,因此,可選擇不執行活動t1,直接執行活動t2。

2)對活動t2進行驗證:

FVbegl(t2)= min{Token(·p2)2}+

Vl(·p2)+Vl(t2)=3

FVendc(t2)= max{Token(·p2)1}+

Vc(·p2)=8

由于FVendc(t2)-FVbegl(t2)=6>5,因此活動t2為可調度的。

3)對活動t3進行驗證:

FVbegl(t3)= min{Token(·p3)2}+Vl(·p3)+

Vl(t3)=9

FVendc(t3)= max{Token(·p3)1}+

Vc(·p3)=15

由于FVendc(t3)-FVbegl(t3)=6<7,因此對活動t3的時間約束進行修正:

(1)減小Vl(t3)的值至0,則FVendc(t3)-FVbegl(t3)=7,可調度。

(2)活動t3新的時間約束為[0,3],活動t3新的最早觸發開始時間值與最晚觸發結束時間值分別為:

Vl(·p3)+Vl(t3)=8

4)對活動t4進行驗證:

FVbegl(t4)= min{Token(·p4)2}+

Vl(·p4)+Vl(t4)=18

FVendc(t4)= max{Token(·p4)1}+

Vc(·p4)=25

由于FVendc(t4)-FVbegl(t4)=7≥5,因此活動t4為可調度的。

5)對活動t5進行驗證:

FVbegl(t5)= min{Token(·p5)2}+

Vl(·p5)+Vl(t5)=28

FVendc(t5)= max{Token(·p5)1}+

Vc(·p5)=34

由于FVendc(t5)-FVbegl(t5)=6>4,因此活動t5為可調度的。

6)對活動t6進行驗證:

FVbegl(t6)= min{Token(·p6)2}+

Vl(·p6)+Vl(t6)=37

FVendc(t6)= max{Token(·p6)1}+

Vc(·p6)=42

由于FVendc(t6)-FVbegl(t6)=5≥4,因此活動t6為可調度的。

7)對活動t7進行驗證:

FVbegl(t7)= min{Token(·p7)2}+

Vl(·p7)+Vl(t7)=42

FVendc(t7)= max{Token(·p7)1}+

Vc(·p7)=50

由于FVendc(t7)-FVbegl(t7)=8≥7,因此活動t7為可調度的。

8)對活動t8進行驗證:

FVbegl(t8)= min{Token(·p8)2}+Vl(·p8)+

Vl(t8)=54

FVendc(t8)=max{Token(·p8)1}+Vc(·p8)=62

由于FVendc(t8)-FVbegl(t8)=6≥5,因此活動t8為可調度的。

9)對活動t9進行驗證:

FVbegl(t9)= min{Token(·p9)2}+Vl(·p9)+

Vl(t9)=62

FVendc(t9)= max{Token(·p9)1}+

Vc(·p9)=71

由于FVendc(t9)-FVbegl(t9)=9≥5,因此活動t9為可調度的。

10)對活動t10進行驗證:

FVbegl(t10)= min{Token(·p10)2}+

Vl(·p10)+Vl(t10)=70

FVendc(t10)= max{Token(·p10)1}+

Vc(·p10)=78

由于FVendc(t10)-FVbegl(t10)=8≥7,因此活動t10為可調度的。

11)驗證算法結束。

對不可調度的活動進行修正后的時間約束值如表2所示。其中“/”表示無數據。

表2 修正后的時間約束值

4 結束語

為了更好地解決時間約束下工作流過程的可調度性分析這一問題,本文引入了時間約束Petri網,將工作流中的活動分為關鍵任務和非關鍵任務,提出了可調度性分析的判別方法,并且對于不可調度的活動進行時間約束修正,從而使得整個工作流滿足可調度性。分析結果表明,該方法不僅增強了工作流運行的準確性,還大幅提高了其運行效率。