全國名校橢圓拔高卷(B卷)答案與提示
2019-01-03 10:58:54徐利杰
中學生數理化(高中版.高二數學) 2018年12期
一、選擇題
1.A 2.C 3.D 4.C 5.D 6.B 7.C 8.A 9.D 10.A 11.B 12.C 13.A 14.D 15.D 16.A 17.C 18.C 19.D 20.B 21.B 22.C 23.B 24.C 25.C 26.B 27.A 28.A 29.A 30.D 31.A 32.C
二、填空題
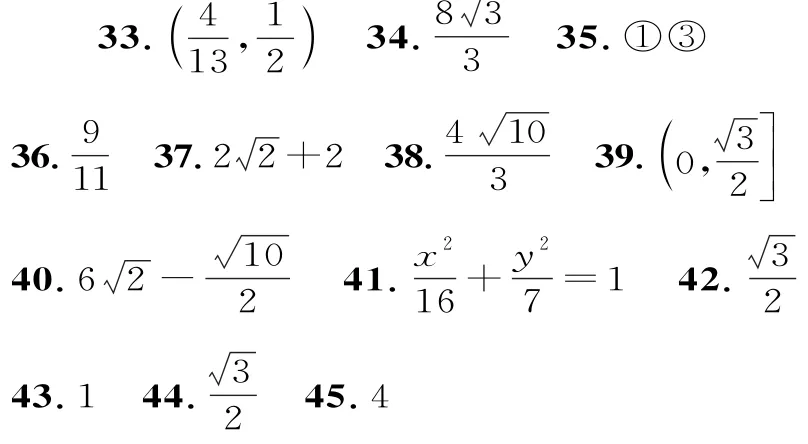
三、解答題


(2)當直線l的斜率為0時,令y=-1,則x=±4,此時以AB為直徑的圓的方程為x2+(y+1)=16。
當直線l的斜率不存在時,以AB為直徑的圓的方程為x2+y2=9。

故兩圓過點T(0,3)。
猜想以AB為直徑的圓恒過定點T(0,3)。對一般情況,證明如下:

故存在以AB為直徑的圓恒過定點T,且定點T的坐標為(0,3)。

(2)由題設知,l1:x=-2,l2:x=2。
切線l與橢圓C的方程聯立消y得:
(1+4k2)x2+8kmx+4(m2-1)=0。①
因為l與C相切,所以①式的Δ=64k2m2-16(1+4k2)·(m2-1)=0,得m2-4k2=1。
l與l1,l2聯立得M(-2,-2k+m),N(2,2k+m)。

49.(1)由題意知橢圓的長軸長2a=22,焦距2c=2。
又由橢圓的定義得|AF1|+|AF2|=2a,所以△AF1F2的周長為|AF1|+|AF2|+|F1F2|=2+2。
(2)由題意得l不垂直兩坐標軸,故設l的方程為y=k(x+1)(k≠0)。

因為P,Q,R到x軸的距離依次成等比數列,所以|yP|·|yR|=|yQ|2。

(2)①由題設知直線斜率存在,設直線l方程為y=k(x+1),則P(0,k)。


51.(1)依題意,直線l顯然不平行于坐標軸,故y=k(x+1)可化為



