面狀要素骨架線提取算法的設計與實現

連超 劉雪

(河南省金地遙感測繪技術有限公司，河南 鄭州 450003)

1 引言

面狀要素的骨架線是對面狀地物主體形狀的抽象描述，反映了面狀地物的主延伸方向和主體形狀特征，在GIS中有著非常重要的應用[1]。其提取方法通常有基于矢量方式和柵格方式兩種，基于矢量方式的主要算法有平行線切割中點連線法和Delaunay三角網法[2-4]。平行線切割中點連線法是最簡單、最直觀求取骨架線的方法，但只能處理簡單的多邊形，對于復雜多邊形（含島多邊形）處理起來比較困難[5]。Delaunay三角網法具有很好的幾何特性、較大的靈活性和可操作性，但工作量較大，內存操作頻繁，占用計算機資源較多，且被應用于平行輪廓時，得到的中軸線會存在很多“鋸齒”[6]。基于柵格方式的方法大多使用數學形態學方法，內存需求少，適應性強，但提取效率低。為此，本文在研究上述算法基礎上，提出了一種新的面狀要素骨架線提取算法，以實現面狀要素骨架線的快速提取。

2 基本定義

圖1中黑線表示基本骨架線，依據文獻[7]對其建立結點 -弧段拓撲關系。結合圖1進行了以下定義：

度——與結點相關聯弧段的個數稱為結點的度。度為1的結點稱為懸掛結點，與懸掛結點相關聯的弧段稱為懸掛弧段；度為3的結點稱為岔口結點。

假岔口結點——對于岔口結點，若多邊形在其附近呈十字路口或丁字路口狀，則稱其為真岔口結點；反之，則稱其為假岔口結點。

節點——組成線段的點稱為節點。對于任意一節點，與其相鄰節點為該節點的鄰節點，與其鄰節點相鄰節點為該節點的跨節點。

角點——三點組成的夾角中，夾角對應的點為角點（如圖1中，∠ABC的角點為B）。

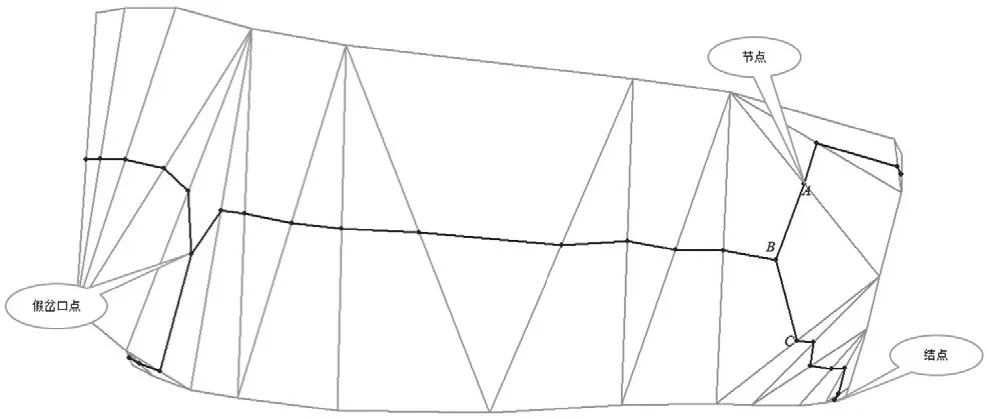
圖1 假岔口結點、節點和角點

3 面狀要素骨架線的提取

3.1 基本思想

首先，依據文獻[8]提取多邊形基本骨架線，結合文獻[7]對基本骨架線建立結點 - 弧段拓撲關系。其次，標記Delaunay三角網中三角形。再次，根據已建立的拓撲關系和三角形標記，對基本骨架線上的結點和弧段集合進行懸掛結點、岔口結點、假岔口結點和懸掛弧段的判斷和標記，并將它們分別存放至各自對應的集合中。然后，根據上述集合對基本骨架線末梢進行分類，根據多邊形節點集合對多邊形進行分類。最后，根據骨架線末梢類型、多邊形類型和最小比例閾值對基本骨架線末梢進行優化。

3.2 Delaunay三角網中三角形的標記

根據基本骨架線和Delaunay三角網中三角形間的空間關系，對Delaunay三角網中三角形進行標記：基本骨架線穿過的三角形標記為true；反之，標記為false。

3.3 懸掛結點、岔口結點、假岔口結點和懸掛弧段的判斷

對于懸掛結點、岔口結點和懸掛弧段，根據其定義進行判斷，并把岔口結點存放至岔口結點集合中，用于假岔口結點的判斷；假岔口結點的判斷是在岔口結點的基礎上，根據其定義進行的。

假設基本骨架線上岔口結點M關聯的三條弧段為L1、L2、L3，L1、L2、L3上的非M結點在其對應弧段上的鄰節點分別為A、B、C，A、B、C三點間兩兩組成線段的中點依次為P1、P2、P3，則判斷M是否為假岔口結點的步驟為：（1）計算出點P1、P2、P3。（2）依據“點是否在多邊形內部判斷方法”判斷出P1、P2、P3是否在多邊形內部。（3）根據步驟2判斷結果和假岔口結點定義，對M進行判斷：若P1、P2、P3都在多邊形內部，則多邊形在M附近沒有呈現十字路口或丁字路口狀，M為假岔口結點；否則，多邊形在M附近呈現十字路口或丁字路口狀，M為真岔口結點。按照上述步驟對圖2中岔口結點O進行判斷可得：O為假岔口結點。

點是否在多邊形內部的判斷方法：首先，找出以點為重心、一定閾值為對角線長度的最小矩形。其次，在Delaunay三角網中找出與最小矩形屬于包含關系的三角形，并將其存入三角形集合中。再次，根據上述結果對該點進行判斷：若集合中沒有三角形或存在標記為false的三角形，則該點在多邊形外部；反之，該點在多邊形內部。

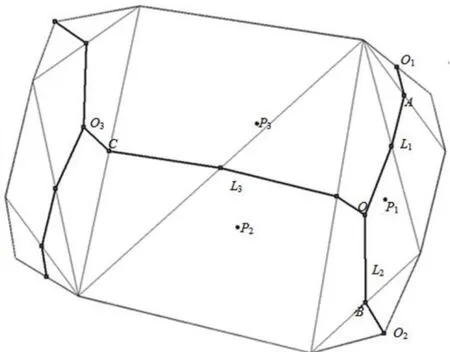
圖2 假岔口結點的判斷

3.4 基本骨架線末梢和多邊形的分類

基本骨架線末梢，是指基本骨架線的末端。根據基本骨架線和懸掛弧段的定義可知；在基本骨架線末梢在懸掛弧段上。因此，本文根據懸掛弧段集合和假岔口結點集合對基本骨架線末梢進行了分類：若懸掛弧段上非末梢處的懸掛結點是假岔口結點，且與該結點相關聯的另兩條弧段中至少有一條為懸掛弧段，則將該結點附近末梢稱為T形末梢；反之，稱為拐角末梢。

對于多邊形，根據其節點個數N進行了分類：若N≠4，稱其為一般多邊形；否則，稱其為四點多邊形。對于四點多邊形，根據其內角進行分類：若時，稱其為似矩形四點多邊形；否則，稱為一般四點多邊形。

3.5 基本骨架線末梢的優化

多邊形分為四點多邊形和一般多邊形。下面分別對這兩種多邊形基本骨架線末梢的優化進行討論。

通過分析四點多邊形基本骨架線末梢類型可知，其都為拐角末梢。因此，四點多邊形基本骨架線末梢的優化實際上是指四點多邊形基本骨架線拐角末梢的優化。四點多邊形基本骨架線末梢的優化步驟為：（1）對四點多邊形進行分類：若其為一般四點多邊形，則保持不變；否則，進入下一步。（2）找出步驟1中四點多邊形每條邊上的中點，并將屬于相對關系兩條邊的中點歸為一組。（3）計算出每組兩點連線間的距離，并進行比較。（4）依據步驟3的比較結果和骨架線最長原則，保留長度值較大兩點間的連線為優化后的骨架線。如圖3（a）中BD表示已構建Delaunay三角網的似矩形四點多邊形的基本骨架線，按照上述步驟對其優化，可得到優化后的骨架線，即圖3（b）中的P2P4。

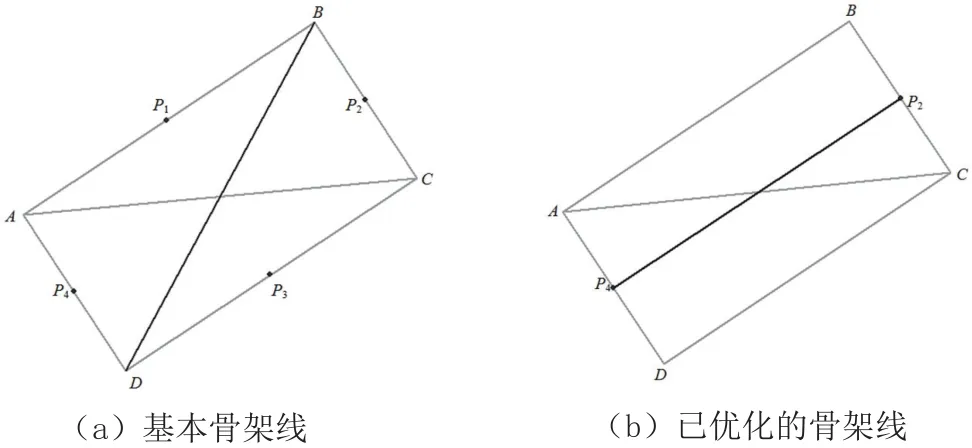
圖3 似矩形四點多邊形基本骨架線末梢的優化

分析一般多邊形基本骨架線末梢類型可知，其既可屬于拐角末梢，又可屬于T形末梢。下面對一般多邊形兩種類型末梢的優化分別進行討論。

（1）拐角末梢的優化。假設一般多邊形基本骨架線拐角末梢處端點為O，則拐角末梢的優化過程為：首先，找出以O為頂點、標記為true的三角形。其次，在找到的三角形中找出以O為端點的兩條邊，并確定這兩條邊的中點M、N。再次，在基本骨架線上找出O的鄰節點和跨節點。最后，依次計算出O、M、N和鄰節點、跨節點組成的以鄰節點為角點的夾角，找出最大角，并將O移至最大角所對應的點（鄰節點、跨節點除外）。如圖4（a）中AI為基本骨架線，其末梢都為拐角末梢，按照上述過程對其優化，可得到優化后的骨架線，即圖4（b）中的P2P4。

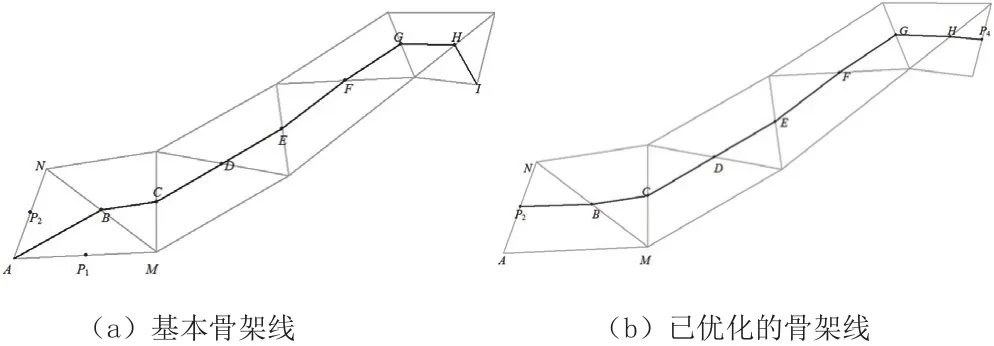
圖4 拐角末梢的優化

（2）T形末梢的優化。它是在已優化拐角末梢的基礎上進行的。假設一般多邊形基本骨架線T形末梢處對應的假岔口結點為O，則T形末梢的優化過程為：

①找出與O相關聯的三條弧段，計算出它們的長度，并進行排序。②分別計算出最長弧段與另兩條弧段的比值以及另兩條弧段間的比值。若前兩個比值都大于最小比例閾值，且最后一個比值接近1，則進入下一步；否則，T形末梢保持不變。③分別判斷較短兩條弧段是否為懸掛弧段。才若都為懸掛弧段，則進入下一步；否則，T形末梢保持不變。④在步驟1中找到的三條弧段上分別找出O的鄰節點和跨節點。⑤找出O所在三角形，計算出三邊的中點，并從中點中找出與O鄰節點（在最長弧段上）坐標相同的點。⑥依據文獻[9]判斷步驟5中找到三角形的類型，若為Ⅰ類或Ⅲ類三角形，則刪除較短的兩條弧段，并將O移至與步驟5中找到點所在三角形的邊屬于相對關系的三角形的頂點即可；否則，進入下一步。⑦依次計算出O在兩條較短弧段上的鄰節點和O在最長弧段上的鄰節點、跨節點組成的以最長弧段上O的鄰節點為角點的夾角，找出較大角所對應的點（最長弧段上結點O的鄰節點和跨節點除外），并判斷不包含該點的弧段（最長弧段除外）是否為懸掛弧段，若為懸掛弧段，則刪除，并將O移至該步驟中已找到的點處即可。如圖5（a）中黑線表示拐角末梢優化后的骨架線，假岔口結點O、M附近的末梢都為T形末梢，按照上述過程對其優化，優化后的結果如圖5（b）中的黑線。

3.6 骨架線提取的步驟

步驟一：提取多邊形基本骨架線，并對其建立結點形 -弧段拓撲關系。

步驟二：標記Delaunay三角網中三角形。

步驟三：標識懸掛結點、岔口結點、假岔口結點和懸掛弧段，并將它們分別存入各自對應的集合中。

步驟四：對基本骨架線末梢和多邊形進行分類。步驟五：對四點多邊形的基本骨架線進行優化。步驟六：對一般多邊形的基本骨架線進行優化。

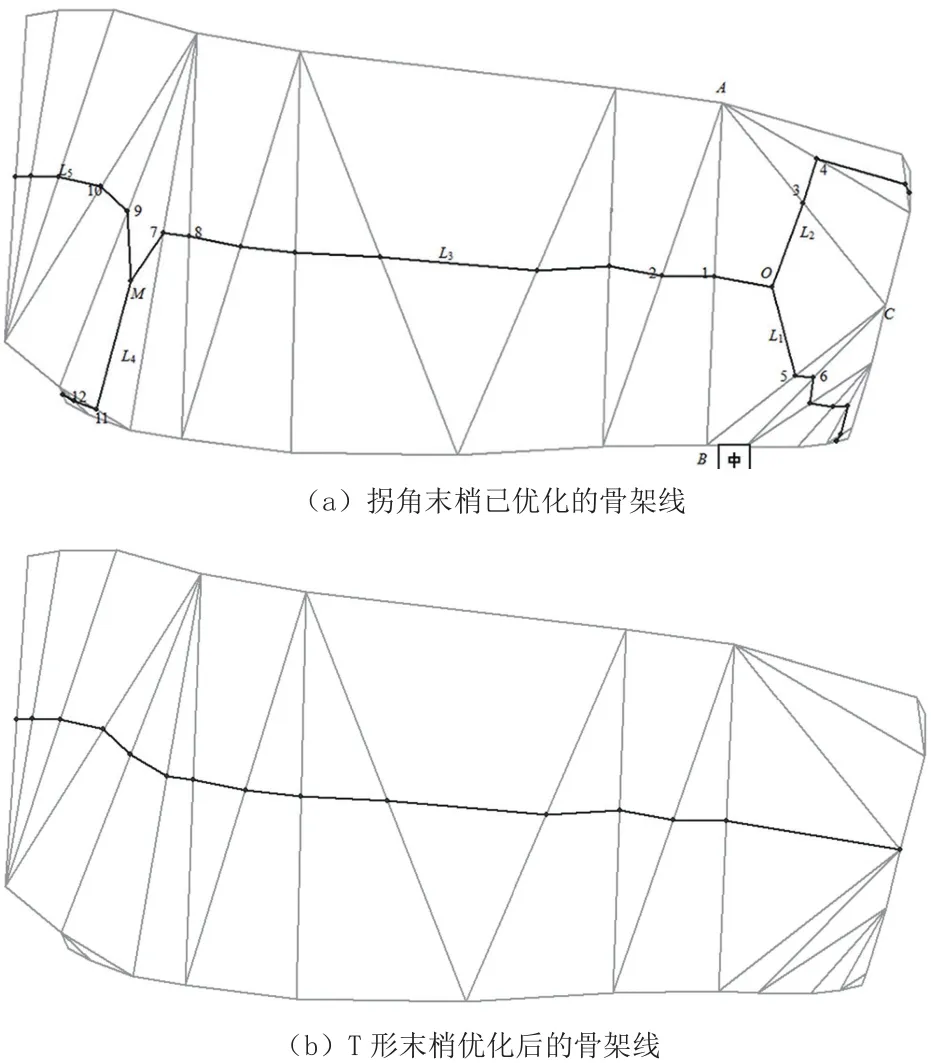
圖5 T形末梢的優化

4 試驗分析

筆者運用這一算法，以某地區地面支渠數據為例，進行了面狀要素骨架線提取。如圖6（a）表示地面支渠原始數據，圖6（b）表示運用本文算法提取的骨架線。分析結果可知，該算法不僅有效解決了提取平行輪廓或似平行輪廓中軸線時出現的“鋸齒”，而且較好反映了面狀地物的主延伸方向和主體的形狀特征，準確性較高。

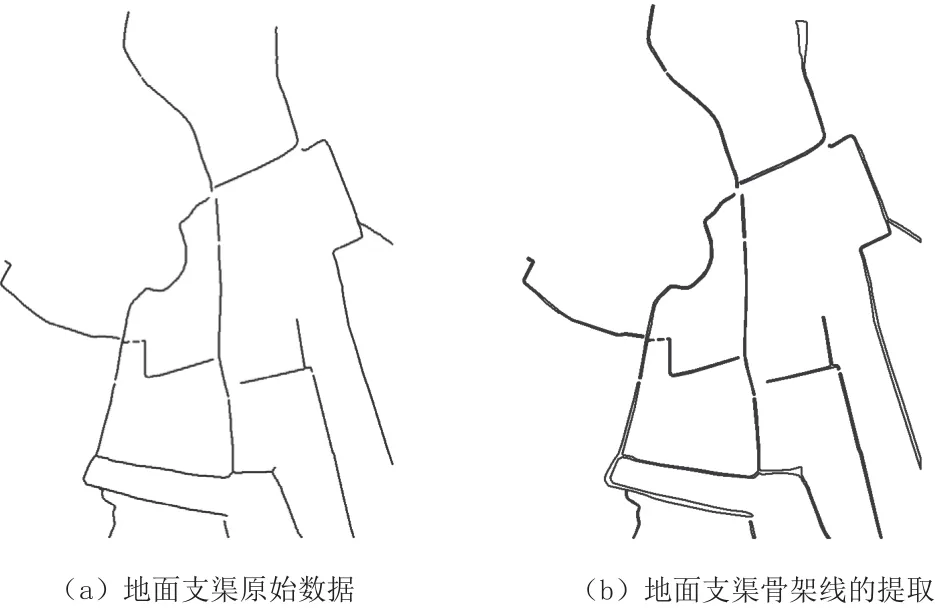
圖6 地面支渠骨架線的提取

5 結束語

本文所用方法實現了面狀要素骨架線的提取，利用Visual Studio 2010編寫了程序，對某地區地面支渠進行了骨架線的提取。實驗結果表明該方法是可行的，且準確性較高，適合大多數地面支渠數據，但還不太成熟，特別是在地面支渠數據比較復雜的情況下，優化后的骨架線并不理想。這些問題需要在以后的研究過程中進一步改善，使其更加實用化。