湍流對潮流能發電水輪機性能影響數值仿真研究?

譚俊哲， 王 鵬， 袁 鵬， 王樹杰， 司先才

(1.中國海洋大學工程學院， 山東 青島 266100； 2.青島市海洋可再生能源重點實驗室， 山東 青島 266100)

作為一種儲量巨大的清潔可再生能源，潮流能得到了各國科研人員的重視，出現了很多關于潮流能發電水輪機的研究。在實際海域中，影響潮流能水輪機獲能的因素有很多，如地形、來流速度、來流方向、湍流等。其中，湍流對潮流能發電水輪機性能的影響主要有以下幾點：第一，湍流對潮流能發電機組的獲能效率和受力有影響；第二，不同湍流下的潮流能發電水輪機的尾流場有所不同[1]。

在實際的潮流能發電場布放海域中必然存在著湍流。Osalusi等[2]測定了英國Fall of Warness海域的湍流強度為7.9%～8.7%，在漲潮落潮時的湍流強度可達9.5%～10.3%；Milne等測量的英國Sound of Islay距離海底5 m處海域的湍流強度為12%～15%；Thomson等測量的美國Puget Sound海域的湍流強度為6.6%～9%。可見，世界上主要的潮流能資源區的湍流強度都較大。因此，研究湍流條件下潮流能發電水輪機性能及尾流特征是有必要的，多家研究機構進行了湍流對潮流能發電水輪機性能影響的研究。Mycek P等[3]在水槽中對工作在湍流強度分別為3%和15%兩種工況下的直徑為800 mm的潮流能發電水輪機獲能系數和軸向力系數等進行了試驗研究；Rose等[4]在實驗室中用縮放比例為1/10的水輪機模型進行了湍流試驗(原水輪機直徑1.5 m)，研究了不同來流速度下尾流場相關性能；Tedds等[5]主要研究了湍流條件下不同葉片數目、扭角情況下尾流形狀。

上述研究主要從試驗方面進行了湍流對潮流能發電水輪機的相關研究，本文主要從數值模擬方面進行湍流對潮流能發電水輪機相關性能影響的研究，通過設置不同的湍流強度，研究不同湍流強度對潮流能發電水輪機獲能系數和軸向力系數以及尾流場性能的影響，從而為潮流能發電水輪機多機組陣列排布提供合理參考。

1 特征量介紹

1.1 湍流強度

湍流強度(I)簡稱湍流度或湍強，湍流是流體的一種流動狀態。當流速很小時，流體分層流動，互不混合，稱為層流；當流速增加到很大時，流線不再清楚可辨，流場中有許多小漩渦，層流被破壞，相鄰流層間不但有滑動，還有混合。這時的流體作不規則運動，有垂直于流管軸線方向的分速度產生，這種運動稱為湍流。實際水域中湍流強度可通過以下公式計算得到[6]：

(1)

式中：I-湍流強度；σ-平方差；u-x方向水流速度(m·s-1)；v-y方向水流速度(m·s-1)；w-z方向水流速度(m·s-1)。

1.2 獲能系數、軸向力系數

分析水輪機特性時，表征水輪機水動力學性能的常用參數是功率系數、軸向力系數。其中功率系數直接關系到水輪機的發電效率；軸向力系數與潮流對支撐水輪機的軸向力有關系，主要用于對支撐結構進行設計和校核，對保證水輪機安全性和穩定性具有重要影響。功率系數和軸向力系數的表達式[8]為：

(2)

(3)

式中：P電-水輪機實際功率；F-軸向力；ρ-水的密度；V—來流速度；R-水輪機半徑。

在數值仿真中，可通過Fluent計算獲得相應的轉矩T，則水輪機功率為：

P電=Tω。

(4)

式中ω—水輪機角速度。

2 數值建模

1.1 計算模型

本文選用直徑600 mm潮流能發電水輪機模型，翼型為NACA 63418，具體參數如表1所示。

表1 潮流能發電水輪機模型相關參數Table 1 Related parameters of tial turbine model

根據MATLAB生成的葉片翼型數據及轉子的尺寸參數，在三維繪圖軟件中完成不同直徑轉子的水輪機建模，其三維模型如圖1所示。

圖1 水輪機轉子三維模型Fig.1 3D model of tidal turbine rotor

將潮流能發電水輪機三維模型導入到Gambit中進行網格劃分(見圖2)。考慮到水輪機尾流場的充分擴展，流場域的尺寸選取為：長×寬×高=25D×5D×5D。水輪機采用三角形非結構面網格，旋轉域和流場域均采用六面體非結構體網格。通過控制面網格、旋轉域網格、流體域網格尺寸，實現了旋轉域的局部加密，加密程度約為10倍網格加密，從而使模擬結果更精確。

圖2 網格劃分Fig.2 Meshing

水輪機的計算區域如圖3所示。水輪機中心距離入口為5D處，既提高了計算效率，節省了計算時間，同時又保證了計算準確性；為避免計算域上下邊界對水輪機的干擾，選取上下邊界距離水輪機中心2.5D；考慮尾流在水輪機后方大約20D處完全恢復，故出口邊界在水輪機中心后方25D處[9]。

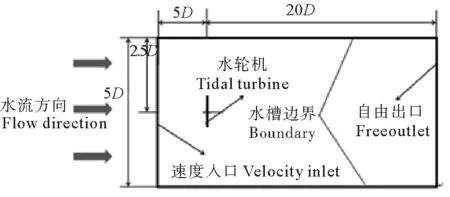
圖3 水輪機計算區域Fig.3 The area of computation about tidal turbine

1.2 邊界條件設定

鑒于水為不可壓縮液體及來流速度已知，設置進口邊界為速度入口(Velocity inlet)，出口邊界條件為壓力出口(Pressure outlet)，水輪機葉片表面為無滑移的固壁條件(Wall)；旋轉域和流體域的類型都為流體(Fluid)。

1.3 湍流模型選擇

湍流模型的選擇。假設流體為黏性不可壓縮的液體，則流體運動方程為納維-斯托克斯(N-S)方程，其三維流動連續性微分方程[10]為：

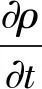
(5)

式中:u-速度矢量(m·s-1)；-拉普拉斯算子；ρ-流體密度(kg·m-3)。

鑒于Realizable 模型已經廣泛應用于旋轉剪切流、包含有射流和混合流的自由流動、邊界層流動，以及帶有分離的流動，故本數值模擬選取Realizable 模型[11]，關于k和的輸運方程如下：

(6)

(7)

式中:k-湍流動能；ε-湍動耗散率；σk，σε-湍動能k和湍動耗散率對應的Prandtl數，σk=1.0，σε=1.2；xi、xj-位置坐標分量；ui-速度坐標分量；Gk-平均速度梯度引起的湍流動能k的產生項；μ-流體動力黏性系數。湍流黏性系數μ=ρCμk2/σε，Cμ-模型常數，C2=1.9。

3 數值模擬結果

來流速度分別為0.4、0.6、0.8、1.0、1.2 m/s時不同湍流強度下(3%和15%)水輪機獲能系數、軸向力系數和尾流場流速損失如圖4～6所示。

如圖4所示，對兩種湍流強度，當尖速比在3～6時水輪機獲能系數較高；湍流強度為3%時各曲線更接近一條曲線，而湍流強度為15%時各曲線比較分散；對應每種來流速度下，湍流強度為3%時水輪機獲能系數略高于湍流強度為15%時；獲能系數隨來流速度的增大而有所增加，來流速度為1.2 m/s時最大獲能系數比來流速度為0.4 m/s時最大獲能系數高10%左右。

如圖5所示，軸向力系數受湍流強度影響不是很大，相同來流速度下，湍流強度小，軸向力系數較大；對同一湍流強度下，來流速度大，軸向力系數較大，但來流速度為1.2 m/s時最大軸向力系數跟來流速度為0.4 m/s時最大軸向力系數差別不是很大。

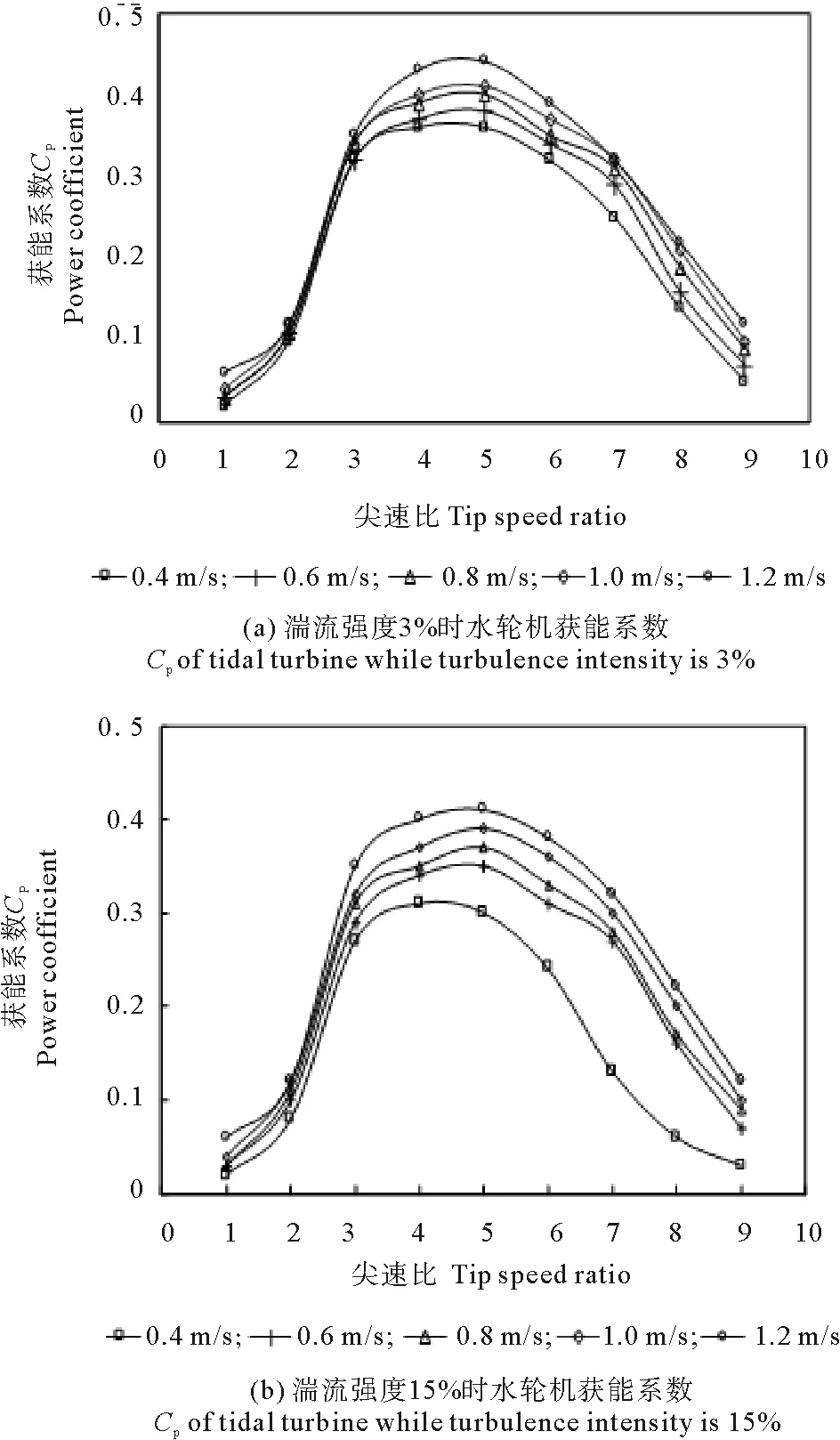
圖4 不同湍流強度時水輪機獲能系數Fig.4 Cp of tidal turbine when turbulence intensity is different

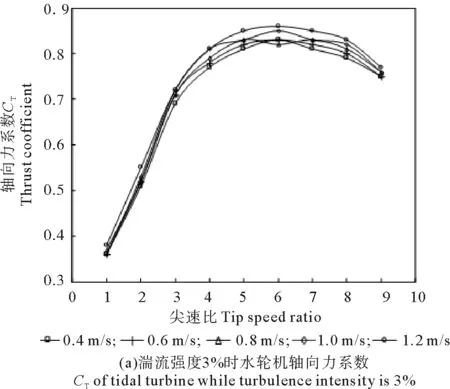
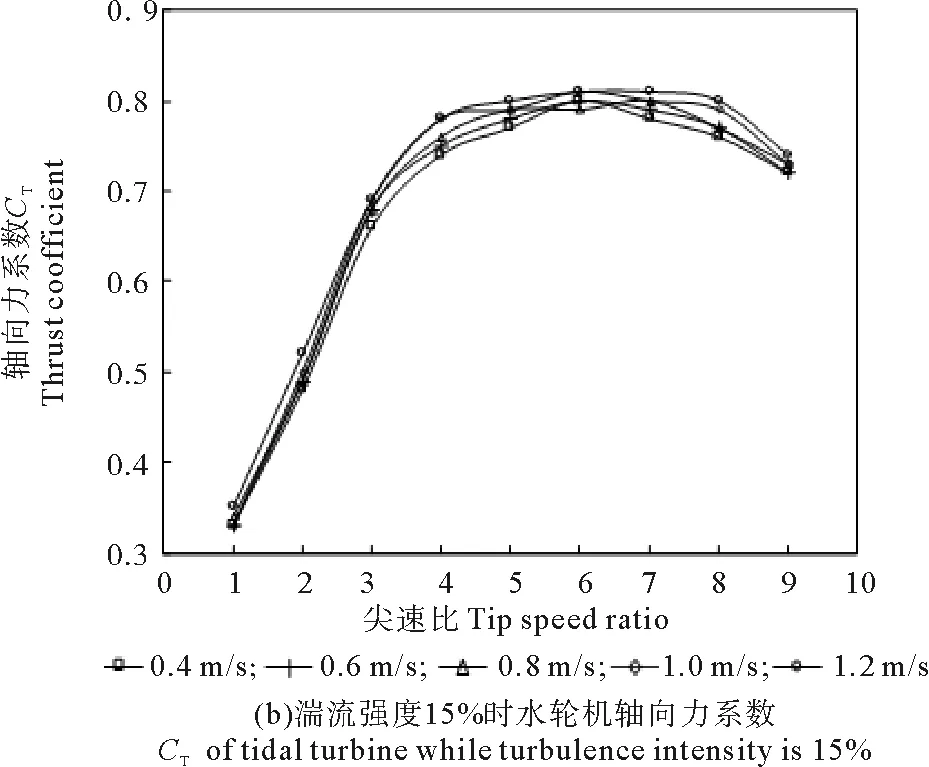
圖5 不同湍流強度時水輪機軸向力系數Fig.5 CT of tidal turbine when turbulence intensity is different

如圖6所示，不同湍流強度時，水輪機后方相同位置處軸向速度損失不同，且湍流強度越小，水輪機后方軸向相同位置處速度損失越大；湍流強度為3%時，水輪機后方軸向10D位置處速度損失依然在20%左右，而對于湍流強度為15%時，在水輪機后方軸向5D處速度損失可達到10%，即尾流場速度恢復更快。

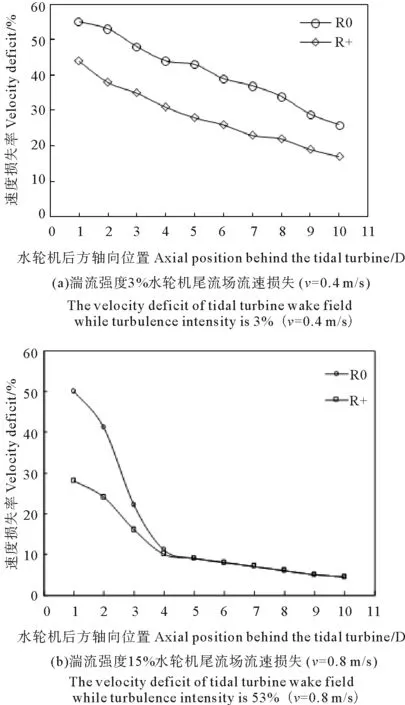
(尖速比為5，R0為水輪機中心，R+為水輪機半徑。The tip speed ratio is 5, R0 represents the center of tidal turbine, R+ represents the radius of tidal turbine.)

圖6 不同湍流強度時水輪機尾流場流速損失
Fig.6 The velocity deficit of tidal turbine wake field while turbulence intensity is different

數值仿真中得到了相同來流速度下，不同湍流強度時水輪機后方尾流場速度云圖及湍流強度云圖，如圖7、8所示。

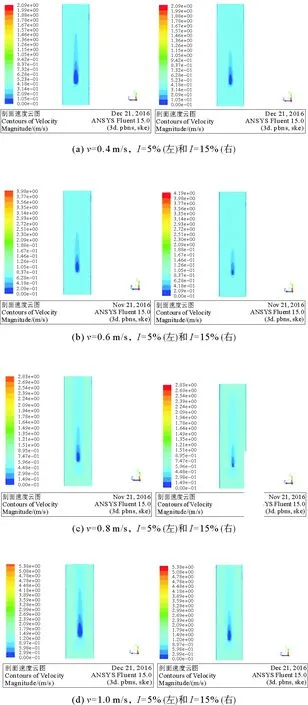
圖7 不同湍流強度尾流場速度云圖對比圖Fig.7 Cloud graphics of wake field velocity magnitude under different inlet flow turbulent intensity

圖8 不同湍流強度尾流場湍流強度云圖Fig.8 Cloud graphics of wake field turbulent intensity under different inlet flow turbulent intensity

如圖7所示，相同來流速度時，湍流強度不同，尾流場長度也不同，且湍流強度越大，尾流場越小，即尾流場速度恢復越快，前排水輪機對后排水輪機影響更小。

如圖8所示，相同來流速度時，湍流強度不同，流過水輪機后尾流場湍流強度也不同，且湍流強度越大，尾流場軸向和徑向影響范圍越大。

4 與相關文獻的試驗結果進行對比

為了驗證數值模擬結果的準確性，將模擬結果與文獻[2]中的試驗研究結果進行對比。文獻[2]中Mycek P等[2]關于獲能系數、軸向力系數和尾流場速度損失試驗研究結果如圖9(a～c)所示。

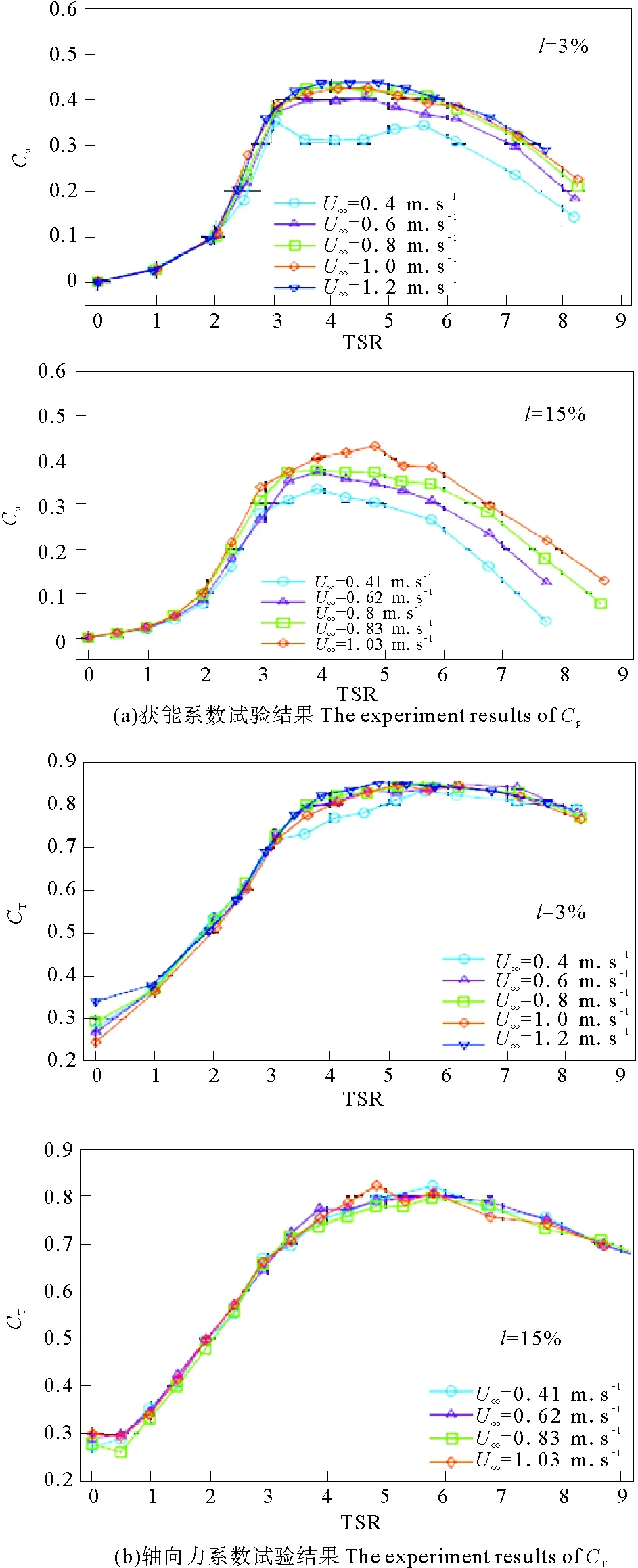
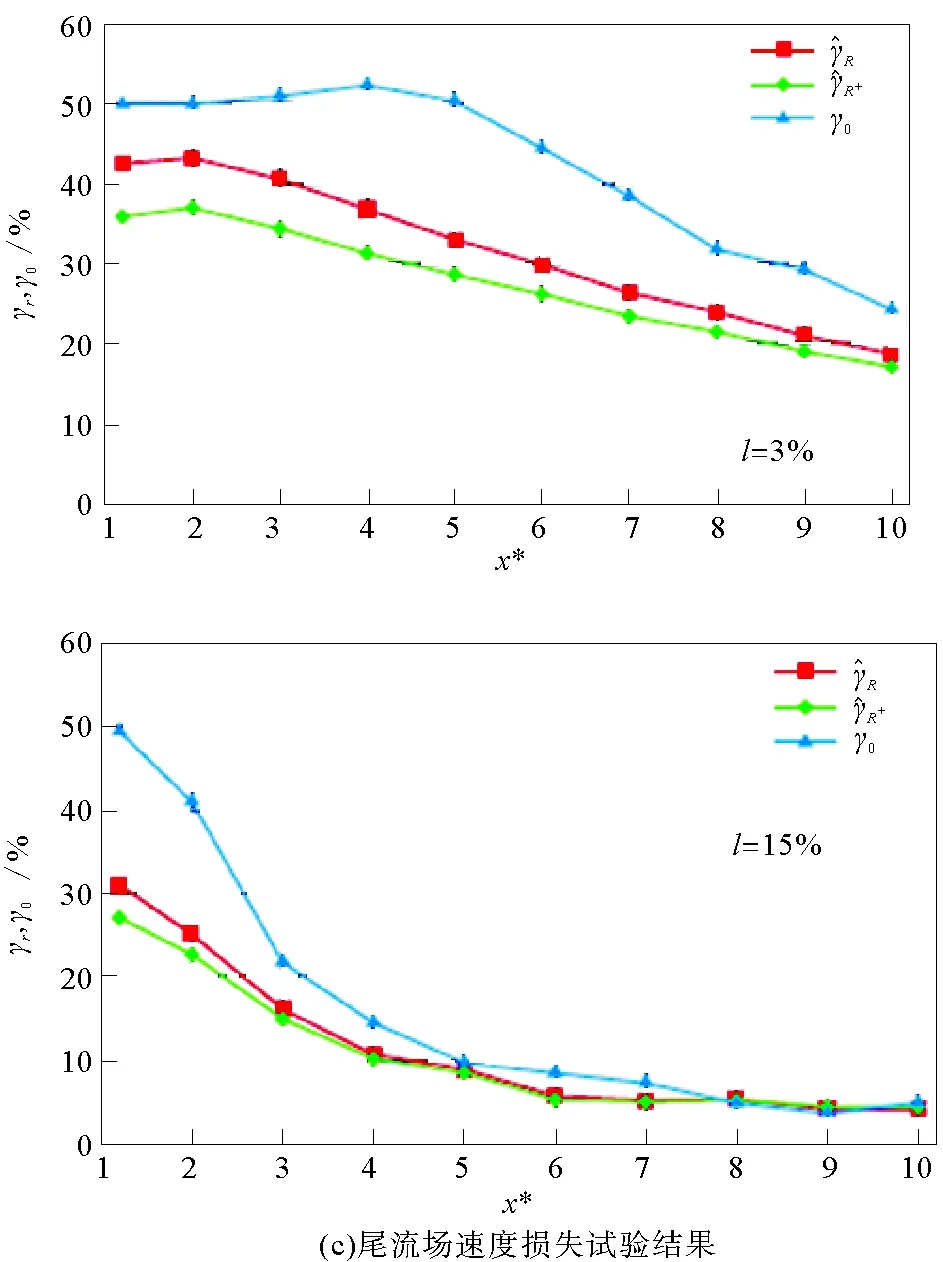
圖9 Mycek P等[2]部分試驗結果Fig.9 The experiment results of Mycek P

將如圖4～6所示的不同湍流強度時水輪機獲能系數、水輪機軸向力系數和水輪機尾流場流速損失與如圖9所示的文獻[2]中Mycek P等的試驗研究結果進行對比，兩者的結果比較接近，變化趨勢基本一致。可見，利用CFD軟件對處于不同湍流強度下的潮流能發電水輪機性能進行數值模擬結果是可靠的。

5 結論及展望

通過對數值模擬結果進行分析，并與相關文獻[2]中的試驗結果進行對比，兩者結果比較符合，可以得到以下結論：

(1)當來流速度相同時，湍流強度越大，水輪機獲能系數越小；當湍流強度相同時，來流速度越大，獲能系數越高。當存在湍流時，水輪機的獲能效率降低，獲能系數最大可降低10%左右。

(2)湍流強度越大，水輪機軸向力系數略有減小；當湍流強度相同時，流速越大，軸向力系數也越大。

(3)湍流強度越大，水輪機后方尾流場流速恢復越快，當湍流強度為3%時，水輪機后方軸向10D處只恢復到80%左右，而當湍流強度為15%時，水輪機后方軸向5D處即可恢復到90%左右。因此，湍流強度對第二排水輪機的排布位置具有明顯的影響，湍流強度越大，適合安放第二排水輪機的前后間距越小。

由于計算時間的原因以及與文獻[2]對比的需要，數值模擬中只設置了兩種典型的湍流強度。在后續研究中可對湍流強度進行進一步的細化，從而為湍流對潮流能發電水輪機的影響進行更加深入的研究。