基于改進蟻群算法的鐵路乘務排班計劃編制

王東先　孟學雷　何國強　孫慧萍　王喜棟

摘 要：為了提升鐵路乘務排班計劃編制的質量和效率，將乘務排班計劃編制問題抽象為單基地、考慮中途休息的多旅行商問題（MTSP），建立以排班周期最小、乘務交路間冗余接續時間分布最均衡為優化目標的單一循環乘務排班計劃數學模型，并針對該模型提出了一種啟發式修正蟻群算法。首先，構建滿足時空約束的解空間，分別對乘務交路節點和接續路徑設置信息素濃度;然后，確定基于修正的啟發式信息，規定螞蟻按乘務交路順序依次出發，使螞蟻遍歷所有乘務交路;最后，從不同的乘務排班方案中選擇最優的排班計劃。以廣深城際鐵路為例對所提模型及算法進行驗證，并與粒子群算法進行對比。實驗結果表明：在相同的模型條件下，采用啟發式修正蟻群算法編制的乘務排班計劃平均月工時降低了8.5%，排班周期降低了9.4%，乘務人員超勞率為0。所提模型和算法能夠壓縮乘務排班周期，降低乘務成本，均衡工作量，避免乘務人員超勞。

關鍵詞：鐵路;乘務排班計劃;多旅行商問題;冗余時間;啟發式修正蟻群算法

中圖分類號： TP301.6（算法理論）;U292.4（列車運行組織及調度工作） 文獻標志碼：A

Railway crew rostering plan based on improved ant colony optimization algorithm

WANG Dongxian1， MENG Xuelei1*， HE Guoqiang1， SUN Huiping1， WANG Xidong2

（1. School of Traffic and Transportation， Lanzhou Jiaotong Unirersity， Lanzhou Gansu 730070，China;

2. Wuwei South Station， China Railway Lanzhou Group Company， Limited ， Wuwei Gansu 733000， China）

Abstract： In order to improve the quality and efficiency of railway crew rostering plan arrangement， the problem of crew rostering plan arrangement was abstracted as a Multi-Traveling Salesman Problem （MTSP） with single base and considering mid-way rest， a single-circulation crew rostering plan mathematical model aiming at the smallest rostering period and the most balanced distributed redundant connection time between crew routings was established， and a new amended heuristic ant colony optimization algorithm was proposed aiming at the model. Firstly， a solution space satisfying the spatial-temporal constraints was constructed and the pheromone concentration was set for the crew routing nodes and the continued paths respectively. Then， the amended heuristic information was adopted to make the ants start at the crew routing order and go through all the crew routings. Finally， the optimal crew rostering plan was selected from the different crew rostering schemes. The proposed model and algorithm were tested on the data of the intercity railway from Guangzhou to Shenzhen. The comparison results with the plan arranged by particle swarm optimization show that under the same model conditions， the crew rostering plan arranged by amended heuristic ant colony optimization algorithm has the average monthly man-hour reduced by 8.5%， the rostering period decreased by 9.4%， and the crew overwork rate of 0. The designed model and algorithm can compress the crew rostering cycle， reduce the crew cost， balance the workload， and avoid the overwork of crew.

Key words： railway; crew rostering plan; Multi-Traveling Salesman Problem （MTSP）; redundant time; amended heuristic ant colony optimization algorithm

0 引言

乘務排班計劃是乘務計劃的一部分，是以列車運行圖、乘務交路、相關乘務規則、車站設備條件為基本依據編制的乘務人員（司乘）工作計劃。其中，列車運行圖包含了待完成的乘務任務，乘務交路規定了乘務人員擔當運輸任務的固定周轉區段，乘務規則限定了乘務人員的工作時間，車站設備條件限制了車站是否是乘務基地及具備司乘人員換乘或休息的條件。

為了合理優化乘務計劃編制，有效提升編制效率，乘務計劃的編制分為兩個階段：乘務交路計劃、乘務排班計劃。乘務交路計劃和乘務排班計劃既有聯系又有區別，兩者相輔相成，兩者既遵循一定的共性乘務規則，同時又具有自身的獨特特點。通過乘務交路計劃得到乘務交路，利用乘務交路編制乘務排班計劃。乘務排班計劃編制的優劣直接決定了鐵路機務部門的運營效率及機務人員的勞動強度。本文針對乘務排班計劃編制問題作出進一步討論。文獻[1]將乘務人員排班計劃和飛機排班計劃綜合考慮，建立了動態規劃模型，具有更好的魯棒性，但是該模型對于求解“點多線長”的鐵路乘務計劃具有一定局限性。文獻[2]將改進的遺傳算法應用于乘務排班計劃的綜合優化問題，雖然編制效率顯著提高，但該模型和算法得到的排班計劃超勞率偏高。文獻[3]將乘務排班計劃編制劃分為兩階段問題，并用分支定界法進行了求解。文獻[4]建立整數規劃模型，運用拉格朗日松弛和列生成的組合優化算法，對應急條件下擾動時間不確定的乘務排班計劃問題進行研究，但該模型沒有考慮乘務人員工作量的均衡性。文獻[5]重點研究了工作效率對于乘務計劃編制的影響，采用蟻群算法進行求解，但未考慮乘務交路的均衡性。文獻[6]利用雙重策略蟻群算法編制了乘務交路計劃，但是對乘務排班計劃的編制沒有作進一步研究。文獻[7]利用SE（Simulated Evolution）方法編制乘務排班計劃，但是對乘務交路計劃的編制沒有深入研究。文獻[8]首次在國內將列生成技術應用到了乘務排班計劃的編制，并把乘務排班計劃問題抽象成了旅行商問題，但是該算法在求解初始可行解時效率較低。文獻[9]將乘務排班計劃問題抽象為網絡流模型，并利用拉格朗日松弛算法進行求解，但是該算法的迭代步長由經驗公式自行設定，缺乏論證。文獻[10]將高速鐵路乘務排班計劃的編制轉化為特殊的旅行商問題，并采用改進的蟻群算法進行求解，該模型雖然能夠有效提高編制效率，但模型中沒有考慮乘務排班的月工時是否超勞。文獻[11]將乘務計劃編制問題拆分為最優回路構造、回路循環優化和排班三個子問題，并設計了遺傳算法進行求解，但是編制步驟繁瑣，不利于鐵路乘務排班計劃的快速編制。文獻[12]將乘務排班計劃編制問題劃分為給定周期、單一循環乘務排班計劃兩類排班形式，并對非極大排班方案的調整作了深入研究，設計了基于貪婪搜索、集合覆蓋的兩階段求解算法，但是該模型沒有考慮乘務交路計劃與乘務排班計劃的協同優化。文獻[13]根據現場調研統計的結果，建立了基于乘務人員偏好的乘務交路計劃，但是對于復雜交路，沒有給出具體的評價值標定方法。文獻[14]以交路單元作為列車乘務交路編制基本單位的方法，建立了以最小費用為目標的乘務交路編制優化模型，利用基于貪婪思想的啟發式算法進行求解，但是求解精度仍存在改進空間。文獻[15]利用禁忌搜索算法完成系統功能設計，能夠快速編制高速動車組乘務交路方案，但是機車乘務員容易超勞。文獻[16]在已知乘務員標準月工時的前提下，建立了以交路和乘務工時為主要約束條件，以乘務班組最少、乘務費用最低為優化目標的模型，并利用遺傳算法進行求解;該模型和算法可有效降低鐵路部門乘務費用，但乘務人員工作量較大，不利于行車安全。對上述研究成果進行分析可以看出，國內大多數學者的研究重點主要集中于求得乘務周期最小的排班方案，而關于冗余接續時間相對均衡的排班方案的研究較少。冗余接續時間的均衡性不僅關系到乘務值乘計劃的穩定性，還與乘務人員作息是否規律有密切的關系。

根據文獻[6]已編制的乘務交路計劃，本文在此基礎上利用乘務交路，繼續編制乘務排班計劃。文獻[6]將乘務交路計劃編制問題抽象為單基地、均衡行駛路程的多旅行商問題（Multi-Traveling Salesman Problem， MTSP），通過引入均衡因子，建立了以乘務交路用時少和子乘務交路間任務均衡為目標的數學模型。針對該模型文獻[6]提出了一種雙重策略蟻群優化算法，該算法設計了雙重信息素及雙重策略狀態的轉移概率，結合乘務交路時空約束規則，設置了雙重信息素全局更新策略，在每次迭代結束后，只允許全局最優解釋放信息素。在最優路徑上，螞蟻才釋放信息素，同時信息素揮發，這點非常重要，因為在信息素更新時的時間復雜度從O（n2）降到了O（n）。設置雙重策略狀態的轉移概率，增加了螞蟻搜索路徑的多樣性，又使得更新的路徑具有隨機性，能夠有效避免算法過早地陷入局部最優。本文在總結已有研究成果的基礎上，結合鐵路乘務規則及其特點，將乘務排班計劃編制問題抽象為單基地、考慮中途休息的多旅行商問題，建立以排班周期最小、乘務交路間冗余接續時間分布最均衡為優化目標的單一循環乘務排班計劃數學模型，并針對該模型提出了一種啟發式修正蟻群算法。該算法對解空間作了改進，構建n維向量Crew-scheduling，設計了基于啟發式信息修正的轉移概率。通過啟發式信息修正的轉移概率，使算法在降低問題復雜性的同時，增加螞蟻搜索路徑的多樣性，減少算法搜索的盲目性，有效引導算法朝全局最優方向進行搜索。啟發式信息在算法運行時，能夠指引螞蟻向壓縮乘務交路總接續時長的相鄰乘務交路轉移。文獻[6]選用遺傳算法作為對比算法，得出改進的雙重策略蟻群優化算法較遺傳算法能更快地收斂，解的質量也有大幅提升。本文選用粒子群算法作為對比算法，得出改進的啟發式修正蟻群算法較粒子群算法具有更快的收斂速度。同時，文獻[6]和本文都運用廣深線城際鐵路數據作為算例，對設計的模型及算法進行檢驗。

1 乘務排班計劃數學模型的建立

1.1 問題描述

螞蟻k從不同的乘務交路節點出發，以概率Pkij向相鄰乘務交路j轉移時，若轉移后的連續值乘累計時長小于單雙休累計值乘時長標準，則直接轉移至乘務交路j，同時更新向量Crew-scheduling，并令值乘累計時長為tcj=tci+ttj;若轉移后連續值乘累計時長大于單雙休累計值乘時間標準，則按照單雙休累計值乘時長標準轉移至乘務交路j，同時更新向量Crew-scheduling，令值乘累計時長為tcj=tcj，并將轉移后的乘務交路j定為當前節點，繼續進行解的構建，直至向量Crew-scheduling中所有元素都為1時完成解的構建。

3）信息素的表示、初始化及更新。

信息素τij表示螞蟻處在節點i時，接續節點j的重要程度。其中，路徑上的信息素初始濃度設定為：

τij（0）=1|A|2-|A|， i≠j

0，其他? （15）

式中，A表示互異乘務區段節點之間的接續頻數。

信息素濃度與各乘務交路節點是否參與了最優解的構建成正相關。在最優螞蟻每次迭代后，路徑上的信息素的更新取值設定如下：

τij（n+1）=ρτij（n）+Δτij（16）

Δτij=1/Zibest， eij∈sibest

0，其他 （17）

其中：ρ為信息素揮發因子，0<ρ<1;n代表迭代次數;Δτij為每次迭代過程中的信息素增量。

4）基于啟發式信息修正的轉移概率。

當第k只螞蟻在乘務交路節點i時，接續下一個乘務交路j的概率為：

Pkij=[τij]α·[ηij]β∑l∈Vki[τil]α·[ηil]β， j∈Vki

0，其他 （18）

式中：ηij為預見度，表示從乘務交路節點i轉移到乘務交路節點j的預見程度;Vki表示螞蟻待訪問的節點集合，隨著迭代次數的增加，Vki中的元素不斷減少，直至為空，即表示所有乘務交路節點全部遍歷完畢;α表示殘留信息素的相對重要程度，其值越大，信息素的濃度在轉移中起的作用越大;β為預見值的相對重要程度，其值越大，螞蟻以越大的概率轉移到接續時間較短的下一個乘務交路節點。其中對啟發式信息進行修正，如式（19）所示：

ηij=

1ttθij-Ts+ω， tci+ttθij≤Tr

1ttθij0+Ts-ttθij01440·1440-Ts+ω，其他 （19）

其中：ttθij為乘務交路接續時間;Tr為單雙休接續時長標準;Ts為乘務交路間實際接續時間對應的接續時間標準;ttθij0為初始計算得出的乘務交路間接續計算時長，僅滿足乘務交路的正常接續時長標準，即ttθij0≥Ts，但不一定滿足單雙休接續時長標準;ω為常數，確保當實際接續時間與乘務接續時長標準相同時，式（19）仍成立。所建模型以排班周期最小為優化目標，即乘務交路接續時間最小。對于當前乘務交路，若繼續接續后面的乘務交路，并連續值乘累計時長不超過單雙休累計值乘時長標準，則乘務交路接續時長為通過初始計算而得的乘務交路接續時長;若接續后的連續值乘累計時長大于單雙休累計工作時長標準，則乘務交路接續時長需要由初始接續時長作相應修改，如式（20）所示。

ttθij=ttθij0，tci+ttθij≤Tr

ttθij0+Ts-ttθij01440·1440，其他 （20）

通過分析乘務交路乘務接續時長特點，設計了基于啟發式信息修正的轉移概率，使算法在降低問題復雜性的同時，減少了算法搜索的盲目性，有效引導算法朝全局最優方向進行搜索;同時，增加了螞蟻搜索路徑的多樣性，又使得更新的路徑具有隨機性，能夠有效避免算法過早地陷入局部最優，而進入停滯狀態。啟發式信息在算法運行時，能夠指引螞蟻向壓縮乘務交路總接續時長的相鄰乘務交路轉移。在算法迭代過程中，啟發式信息的修正考慮了接續乘務交路后乘務人員休息的類型，即正常休息或單雙休三種情況，并分別進行計算。在算法執行過程中動態地更新，即算法執行至某一時刻時，并不立即接續下一個乘務交路節點，而是先判斷既有乘務交路分別選擇所有可接續的乘務交路后對應休息的種類（正常休息或單雙休），并根據不同乘務人員休息類型及時更新啟發式信息，目的在于使乘務交路接續冗余時間最小，同時增加算法的全局搜索能力，加快算法的收斂。

5）評價函數。

本文以式（1）作為評價函數，評價所有解的質量。

6）終止策略。

螞蟻經過若干次搜索后，找到的解不再改變時，算法終止。

2.2 算法具體實現流程

本文算法具體實現流程如下：

步驟1 令nc←0，k←1，初始化α、β、ρ螞蟻數量、最大迭代次數等參數，并令乘務排班起始乘務交路節點e←1。

步驟2 將m只螞蟻放置在乘務交路節點e，構建一個n維向量Crew-scheduling，該向量中的元素代表了所有的乘務交路，所有元素都為0-1變量。當某一元素對應的乘務交路未被選擇時，該元素為0;否則為1。初始化向量Crew-scheduling，令所有元素初態為0，并計算乘務交路正常接續時長和累計值乘時長。

步驟3 對于螞蟻k，計算接續n維向量Crew-scheduling中乘務交路i后的累計值乘時長tci，若tci>TCj，則按式（20）將既有乘務交路與乘務交路j的接續時長轉化為單雙休接續時長;否則，保持ttθij不變。

步驟4 針對螞蟻k，根據步驟2中更新后的接續時長計算啟發式信息，并得到選擇下一個乘務交路j的概率，同時更新n維向量Crew-scheduling，若此時n維向量Crew-scheduling元素全部為1，則轉下一步;否則轉步驟3。

步驟5 將得到的乘務排班方案中末尾乘務交路節點與起始乘務交路e相連接，完成乘務交路回路的構建。并令k←k+1，若k>m，則轉下一步;否則轉步驟3。

步驟6 所有螞蟻構建乘務交路回路，以式（1）作為評價函數，評價所有解的質量，并確定最優解，根據迭代最優解動態更新啟發式信息。

步驟7 令nc←nc+1，如果nc小于步驟1中指定的最大迭代次數，則更新n維向量Crew-scheduling，轉至步驟2;否則表示所有螞蟻己完成以乘務交路節點e作為起始節點的乘務排班計劃編制。

步驟8 令e←e+1，若e>n，則表示以所有乘務交路為起始節點完成乘務排班計劃編制，轉下一步;否則轉步驟2。

步驟9 算法結束，根據輸出的不同乘務排班方案，輸出最優解。

3 實例驗證及分析

3.1 實驗數據

以廣深線城際列車為例對本文模型和算法的有效性進行驗證。廣深線正線全長147km，共設車站7座，列車最高運行速度200km/h，線路起于廣州市越秀區廣州站，經由廣州市廣州東站、東莞市東莞站、常平站、樟木頭站、深圳市平湖站，終于深圳市羅湖區深圳站。動車組檢修基地設置在廣州東站接軌的石牌動車檢修所。乘務基地設置在廣州東站，深圳站設乘務人員公寓，供在深圳駐班或調休的乘務班組休息。

廣深線乘務運用情況說明：機務乘務組應遵循早出乘早下班，晚出乘晚下班的原則;所有乘務組在乘務基地進行出退乘作業，廣州東—廣州乘務值乘方式為雙班單司機，廣州東—深圳乘務值乘方式為單班單司機。廣深線6：00—24：00的城際列車開行方案中，有18對列車為廣州至深圳直達列車，57對列車為廣州東至深圳直達列車，以廣州東站為乘務基地，以深圳站為換乘站，根據文獻[6]編制的乘務交路計劃可知廣深線城際列車按照18條乘務交路運行，如表2所示。

3.2 算例結果

根據1.2節所述乘務規則約束，輸入乘務交路時間相關的參數，實驗參數可根據現場具體車站的乘務規則作出相應調整。根據廣深線調研數據可得，乘務排班相關時間參數設置為：乘務排班計劃的正常休息時長標準為不低于960min，但是也不宜過長，否則會影響乘務組織效率，因而將最大正常休息時長設定為1110min。雙休最小累計時長標準為2300min，雙休最大累計時長標準為2418min。正整數M的取值為2880，ε取值為1 （在正常情況下，根據乘務基地廣州東的歷史乘務數據，查定得到的數值）。運用本文設計的改進蟻群算法進行求解，其中：信息素重要程度因子α=1，啟發式信息素重要程度因子為5，信息素揮發因子取0.2，螞蟻個數取20，設迭代次數為200，算法重復執行次數為100。在Intel core i7-8550U CPU 1.8GHz、內存8GB的計算機上，運用Matlab R2015b進行求解。

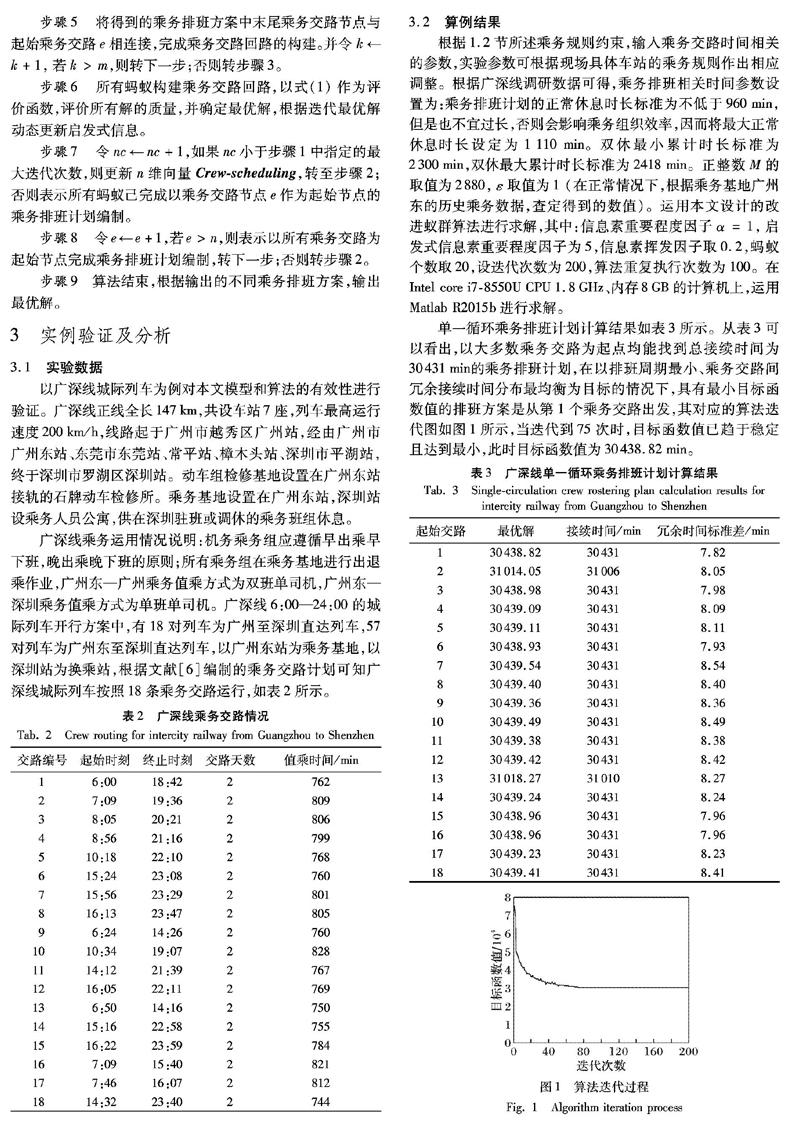
單一循環乘務排班計劃計算結果如表3所示。從表3可以看出，以大多數乘務交路為起點均能找到總接續時間為30431min的乘務排班計劃，在以排班周期最小、乘務交路間冗余接續時間分布最均衡為目標的情況下，具有最小目標函數值的排班方案是從第1個乘務交路出發，其對應的算法迭代圖如圖1所示，當迭代到75次時，目標函數值已趨于穩定且達到最小，此時目標函數值為30438.82min。

各乘務交路間冗余時間的均衡性如圖2所示。從圖2可以看出，乘務交路間冗余接續時間的均衡性比較好。根據計算結果，乘務交路間總接續時間為30431min，乘務人員值乘時間為14100min，所以乘務排班計劃總時間為44531min。

3.3 結果評價分析

計算結果的指標如表4所示，分析后可得出如下結論：

1）本文所求乘務排班周期為48d，排班周期和乘務基地所擁有的乘務組數相同。根據計算結果，所有乘務組均連續作業6d后，休息2d。乘務人員在6d值乘時間里，正常累計值乘時間分布在2301～2418min，平均每天值乘6.392～6.717h，符合乘務人員勞動時間標準。整個乘務排班周期內，乘務員的乘務工作安排如表5所示。

指標名稱實驗結果評價原則評價結果平均月工時178.8h月度最大工時為180h符合最大連續值乘

列數4列連續值乘不得超過

4趟列車符合最大值乘列數5列最大值乘列數不得

超過6趟列車符合最大連續值乘

時間373.8min最大連續值乘時間

不超過480min符合最大值乘時間507min最大值乘時間不超過

540min符合

2）根據優化結果，平均月工時為178.8h，各乘務組的月度工作時間接近規定時間，有效地避免了乘務組超勞的情況，使乘務人員有更充沛的精力值乘后續列車，有效地保障了列車運行安全。調休乘務組和值乘乘務組比例為1/3，比例適中，便于處理臨時性應急乘務任務，并保證了乘務任務分配的均衡性。

3）乘務交路間的冗余時間分布在99～124min，提高了乘務排班計劃的魯棒性，使乘務交路的實際接續時間在列車發生突發事件后仍滿足接續時間標準。

3.4 算法對比分析

多數學者均采用粒子群算法求解乘務排班計劃問題，因此本文以粒子群算法作為對比算法。在同一臺計算機上運用Matlab R2015b對本文模型進行求解，均衡因子與上述取值相同，迭代次數為200，算法重復執行次數為100。從多次執行情況來看，其平均收斂代數約在85～95，每次搜索耗時1.8620s，算法總的執行時間為1023.3240s。起始交路為12號乘務交路，較優乘務排班計劃的運行結果為31439.4117min。兩種算法對比結果如表6所示。通過對比分析可得，與粒子群算法相比，本文設計的改進蟻群算法具有更快的收斂速度，能夠使平均月工時降低8.5%，排班周期降低9.4%，乘務人員超勞率為0，從而大幅提升了解的質量。

4 結語

本文建立了以排班周期最小、乘務交路間冗余接續時間分布最均衡為目標的MTSP模型，通過引入冗余時間均衡性，使得模型更具實際意義;同時提出了一種啟發式修正蟻群算法，其特點在于采用運行時信息作為啟發式信息來指導蟻群的搜索過程，在一定程度上既增加了算法的全局搜索能力，又可以加快算法的收斂，同時避免了傳統蟻群算法易陷入局部最優的缺點。

與粒子群算法相比，本文提出的改進蟻群算法效率更高、求解質量更好，對本文模型的求解具有很強的適應性。

本文模型及算法可為鐵路機務部門編制乘務排班計劃提供有價值的決策支持，對增強鐵路機務系統統籌協調能力具有實際意義和幫助，可作為鐵路系統乘務管理決策理論的組成部分。本文模型未考慮乘務排班計劃與機車周轉圖的一體化協同編制，對于這一問題的研究將是后續工作的重點。

參考文獻 （References）

[1]MERCIER A， SOUMIS F. An integrated aircraft routing， crew scheduling and flight retiming model [J]. Computers and Operations Research， 2007， 34（8）： 2251-2265.

[2]SOUAI N， TEGHEM J. Genetic algorithm based approach for the integrated airline crew-pairing and rostering problem [J]. European Journal of Operational Research， 2009， 199（3）： 674-683.

[3]NISHI T， SUGIYAMA T， INUIGUCHI M. Two-level decomposition algorithm for crew rostering problems with fair working condition [J]. European Journal of Operational Research， 2014， 237（2）： 465-473.

[4]VEELENTURF L P， POTTHOFF D， HUISMAN D， et al. A quasi-robust optimization approach for resource rescheduling [J]. Transportation Science， 2016， 50（1）： 204-215.

[5]陳海平.高速鐵路乘務組織理論與優化研究[D].北京：北京交通大學，2013：42-61.（CHEN H P. Research on theory and optimization of crew organization of high-speed railway [D]. Beijing： Beijing Jiaotong University， 2013： 42-61.）

[6]王東先，孟學雷，喬俊，等.基于改進蟻群算法的鐵路乘務交路計劃的編制[J].計算機應用，2019，39（9）：2749-2756.（WANG D X， MENG X L， QIAO J， et al. Research on railway crew routing plan based on improved ant colony algorithm [J]. Journal of Computer Applications， 2019， 39（9）： 2749-2756.）

[7]閻永光，黃斌.廣深線城際列車乘務組排班計劃編制方法探討[J].交通運輸工程與信息學報，2010，8（1）：25-29.（YAN Y G， HUANG B. Research on the crew schedule programming method of Guangzhou- Shenzhen intercity trains [J]. Journal of Transportation Engineering and Information， 2010， 8（1）： 25-29.）

[8]程巖巖.我國鐵路乘務調度計劃編制方法的研究與設計[D].北京：北京交通大學，2007：21-30.（CHENG Y Y. Research and design of domestic railway crew scheduling method [D]. Beijing： Beijing Jiaotong University， 2007： 21-30.）

[9]張哲銘，王瑩，陳旭，等.高速鐵路單一循環乘務值乘計劃優化研究[J].鐵道運輸與經濟，2018，40（1）：21-27.（ZHANG Z M， WANG Y， CHEN X， et al. Research on single-circulation crew rostering plan optimization for high-speed railway [J]. Railway Transport and Economy， 2018， 40（1）： 21-27.）

[10]褚飛躍，田志強，倪少權.高速鐵路單循環乘務排班計劃編制模型與算法[J].鐵道學報，2012，34（7）：1-9.（CHU F Y， TIAN Z Q， NI S Q. Model and algorithm for formulation of the single cycle crew rostering plans of high-speed railways [J]. Journal of the China Railway Society， 2012， 34（7）： 1-9.）

[11]黃珊.機車乘務人員運用問題及其輔助編排系統研究[D].長沙：中南大學，2014：30-44.（HUANG S. Locomotive crew scheduling problem and scheduling assistant system [D]. Changsha： Central South University， 2014： 30-44.）

[12]田志強.高速鐵路乘務計劃編制優化理論與方法研究[D].成都：西南交通大學，2011：45-72.（TIAN Z Q. Study on theory and methods of crew planning problem of high-speed railway [D]. Chengdu： Southwest Jiaotong University， 2011： 45-72.）

[13]陳旭，李海鷹，王瑩，等.放射狀路網條件下動車組運用優化研究[J].鐵道學報，2017，39（11）：23-29.（CHEN X， LI H Y， WANG Y， et al. Research on optimization of EMU scheduling for radial HSR network [J]. Journal of the China Railway Society， 2017， 39（11）： 23-29.）

[14]李雯，賈富強，楊睿.基于交路單元的高速鐵路乘務交路編制模型與算法[J].交通運輸研究，2018，4（4）：48-53.（LI W， JIA F Q， YANG R. A model and algorithm of high-speed railway crew scheduling based on routing unit [J]. Transport Research， 2018， 4（4）： 48-53.）

[15]符卓，袁雪瑩.高速動車組乘務交路輔助編制系統研究[J].鐵道運輸與經濟，2019（8）：18-21.（FU Z， YUAN X Y. A research on high-speed EMU crew schedule auxiliary preparation system [J]. Railway Transport and Economy， 2019（8）： 18-21.）

[16]楊國元，史天運，張秋亮.鐵路客運乘務排班計劃編制模型及算法[J].交通運輸系統工程與信息，2016，16（4）：159-164.（YANG G Y， SHI T Y， ZHANG Q L. Model and algorithm for railway passenger crew rostering plan [J]. Journal of Transportation Systems Engineering and Information Technology， 2016，16（4）： 159-164.）

[17]馬良，朱剛，寧愛兵.蟻群優化算法[M].北京：科學出版社，2008：57-73.（MA L， ZHU G， NING A B. Ant Colony Optimization Algorithm [M]. Beijing： Science Press， 2008： 57-73.）

[18]段海濱.蟻群算法原理及其應用[M].北京：科學出版社，2005：212-232.（DUAN H B. Ant Colony Algorithms： Theory and Applications [M]. Beijing： Science Press， 2005： 212-232.）

This work is partially supported by the National Key Research and Development Program of China （2016YFB1200100）， the National Natural Science Foundation of China （71861022， 61563028）.

WANG Dongxian， born in 1992， M. S. candidate. His research interests include operation management and decision optimization of rail transit.

MENG Xuelei， bon in 1979， Ph. D.， professor. His research interests include operation management and decision optimization of rail transit.

HE Guoqiang， born in 1990， M. S. candidate. His research interests include intelligent algorithm， management optimization of warehousing logistics.

SUN Huiping， born in 1993， M. S. candidate. Her research interests include operation management and decision optimization of rail transit.

WANG Xidong， born in 1993， assistant engineer. His research interests include optimization of railway traffic organization， cargo transportation organization.

收稿日期：2019-06-27;修回日期：2019-09-05;錄用日期：2019-09-12。

基金項目：國家重點研發計劃項目（2016YFB1200100）;國家自然科學基金資助項目（71861022，61563028）。

作者簡介：王東先（1992—），男，甘肅武威人，碩士研究生，主要研究方向：軌道交通運行管理與決策優化; 孟學雷（1979—），男，山東泰安人，教授，博士，主要研究方向：軌道交通運行管理與決策優化; 何國強（1990—），男，甘肅白銀人，碩士研究生，主要研究方向∶智能算法、倉儲物流管理優化; 孫慧萍（1993—），女，甘肅定西人，碩士研究生，主要研究方向：軌道交通運行管理與決策優化; 王喜棟（1993—），男，甘肅臨洮人，助理工程師，學士，主要研究方向：鐵路車流組織優化、貨物運輸組織。

文章編號：1001-9081（2019）12-3678-07DOI：10.11772/j.issn.1001-9081.2019061118