基于自適應組合核的魯棒視頻目標跟蹤算法

劉培強，張加惠, 吳大偉, 安志勇

(1.山東工商學院 計算機科學與技術學院,山東 煙臺 264005； 2.山東省高等學校協同創新中心：未來智能計算，山東 煙臺 264005； 3.東北林業大學 交通學院, 哈爾濱 150040)(*通信作者電子郵箱liupq@126.com)

0 引言

目標跟蹤是根據最優估計算法分析視頻中目標的狀態，從而為進一步目標識別、分類等提供有效技術支撐。該技術已經被成功應用于智能視頻監控、導航與定位、醫學處理等領域。當前,目標跟蹤算法可分成生成式模型和判別式模型兩大類。生成式模型主要運用生成模型描述目標特征，通過搜索候選目標來最小化重構誤差，有基于粒子濾波跟蹤算法[1]、meanshift算法[2-3]以及卡爾曼濾波和meanshift融合方法[4]等;然而，該方法往往忽略背景信息，因此當目標發生劇烈變化或遮擋時容易產生漂移。判別式方法通過訓練分類器來區分目標和背景，主要有隨機森林算法[5]、相關濾波器(Correlation Filter, CF)算法[6-17]、結構化支持向量機(Support Vector Machine, SVM)算法[18]，以及深度學習算法[19-21]等，判別式方法能夠顯著區分背景和前景的信息，已成為目標跟蹤的研究主流。

近年來相關濾波器算法已成為目標跟蹤的研究熱點。Bolme等[6]提出誤差最小平方和濾波器(Minimum Output Sum of Squared Error filter, MOSSE)相關濾波跟蹤算法，然而該方法存在著不穩定性，同時缺乏目標尺度估計和多通道等問題。Danelljan等[7]利用嶺回歸算法針對相關濾波進行了改進，提出判別式尺度空間跟蹤(Discriminative Scale Space Tracker, DSST)算法，該算法增加了一個尺度濾波器估計目標尺度，然而該方法僅在尺度窗口增加和降低的趨勢估計上容易產生漂移，導致小尺度的震蕩，因此尺度檢測性能有待提高。Zhang等[8]利用上下文信息改進相關濾波器，提出時空上下文(Spatio-Temporal Context, STC)跟蹤算法，針對貝葉斯框架對目標局部的上下文時空關系進行建模，得到目標與背景的統計相關性，通過調整方差sigma來實現尺度的準確估計。Mueller等[9]利用上下文信息提取負樣本信息，從而進一步增強相關濾波器的分類性能。Liu等[10]將被跟蹤目標分為多個子塊，每個子塊將采用相關濾波進行跟蹤，然后將各子塊響應圖進行融合，其算法優點是針對每個子塊單獨更新，有效解決遮擋問題。針對邊界效應問題，Danelljan等[11]提出了空間正則化判別式相關濾波器 (Spatially Regularized Discriminative Correlation Filter, SRDCF)算法，忽略所有移位樣本的邊界部分像素，在損失函數中引入懲罰項，從而抑制離中心較遠的特征的影響。Henriques等[12]提出核化相關濾波器(Kernelized Correlation Filter, KCF)跟蹤算法，利用循環矩陣增強訓練樣本，使用目標周圍區域的循環矩陣采集正負樣本，利用嶺回歸訓練目標檢測器，根據循環矩陣在傅里葉空間可對角化的性質將矩陣的運算轉化為向量的點積，極大降低了運算量，實驗結果表明該算法具有較高的準確率。朱明敏等[13]融合KCF算法和光流法提出了長時核相關濾波跟蹤算法，針對快速運動具有較強的適應能力。錢堂慧等[14]提出了尺度自適應的KCF跟蹤算法，訓練了多尺度相關濾波分類器，能夠正確估計目標的最佳尺度。李麒驥等[15]利用Lucas-Kanade光流法特征點估計目標尺度變化，解決了核跟蹤濾波器中目標尺度估計問題。Danelljan等[16]針對相關濾波器的訓練樣本進行改進，對高質量的訓練樣本設置較高的權重，對低質量的訓練樣本設置較低的權重，具有穩定的跟蹤性能。Ma 等[17]針對相關濾波器利用K最近鄰(K-Nearest Neighbors, KNN)算法分類重定位技術獲取最佳目標跟蹤位置，該方法合理地使用了目標外觀上下文信息進行重定位。

近年來，相關濾波器算法已和SVM[18]、深度學習[19-21]等方法相融合進一步提高算法性能。Valmadre等[21]提出相關濾波網絡(Correlation Filter Network, CFNet)算法，將相關濾波器融入到卷積神經網絡(Convolutional Neural Network, CNN)架構中，相關濾波器(CF)和卷積神經網絡(CNN)可以互相補償，兩者的結合提高了性能。

在相關濾波器改進算法中，KCF算法利用循環平移提高分類器性能，其高速運算性能已成為較多算法的基準跟蹤器。然而該算法采用高斯核或多項式核等單核形式，但現實目標往往不符合高斯核或多項式核等單核表征，而是多核組合或復合核的形式；同時濾波器更新采用固定參數，不具有場景的自適應性。因此，本文構造了自適應組合核(Self-Adaptive Compound Kernel, SACK)的相關濾波器，將線性核和高斯核的自適應組合作為核函數；同時提出自適應更新算法，利用場景的置信度水平(即利用規范化和歸一化后的極大響應值衡量被跟蹤目標的置信度)自適應調整更新率，該算法具有較高的成功率和精確度。

1 自適應組合核的魯棒目標跟蹤算法

1.1 自適應組合核位置跟蹤濾波器

由于KCF算法具有良好的跟蹤性能，已成為較多目標跟蹤算法的位置跟蹤濾波器。然而KCF濾波器采用單核進行處理目標跟蹤，不能合理表征現實目標，本節提出自適應組合核(SACK)目標跟蹤算法，同時采用方向梯度直方圖(Histogram of Oriented Gradients, HOG)特征和灰度特征作為算法的特征輸入。設被跟蹤目標的訓練樣本為x，循環平移后得到樣本xi，設f(xi)=wTφ(xi)為分類器函數，其中φ(xi)為非線性映射函數，則使正則化結構化風險泛函最小優化問題可表示為：

(1)

其中：yi為期望輸出的高斯分布；λ為正則化參數以保證類器的泛化性能。則式(1)核空間嶺回歸的矩陣表示為：

(2)

其中，w是由φ(X)=[φ(x1),φ(x2),…,φ(xn)]T行向量張成的空間中的一個向量。令w=φ(X)Tα，則：

(3)

由式(3)可知對w的求解可轉換為對α的求解，核嶺回歸問題的解[12]為：

α=F-1(F(y)/(F(kx,x′)+λ))

(4)

式中:α即為求解新的濾波器系數;F-1為傅里葉反變換;kx,x′為訓練樣本的核相關矩陣。在KCF跟蹤算法中，使用單一核(高斯核或多項式核)作為核相關矩陣，而本文將采用線性核和高斯核進行學習，則核相關矩陣kx,x′可定義為：

(5)

Map=F-1(F(kx,z)⊙F(α))

(6)

通過尋找響應圖Map中最大的位置就是所要檢測目標的中心位置。通常，式(5)的系數b是根據經驗設定，而本文提出根據線性核和高斯核的輸出響應得到優化參數，優化參數問題可表示為：

(7)

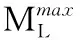
(8)

由于b*的值是由線性核和高斯核的輸出響應計算而得，同時b∈[0,1]，因此由二次函數的性質可修正為：

(9)

當b為1時，表明采用線性核相關矩陣能夠使得風險最小，即目標響應與期望響應的離差平方和最小；當b為0時，表明采用高斯核相關矩陣能夠使風險泛函最小。同時，根據不同b值，自適應調整高斯核相關矩陣和線性核相關矩陣的權重，使其達到泛函最小，式(7)反映了這種自適應性。

為了驗證自適應組合核的必要性，圖1對比了三種核濾波器的跟蹤結果，包括線性核、高斯核和自適應組合核，其中：圖1(a)為被跟蹤目標bolt，圖1(b)為自適應組合核濾波器響應，圖1(c)為三種核跟蹤目標框和質心。

由圖1可以看出，自適應組合核的跟蹤框和質心的準確性明顯優于單純使用高斯核和線性核，自適應組合核同時具有局部核和全局核的優點，因此在目標跟蹤中是必要的，具有一定的優越性。

圖1 不同核濾波器的跟蹤結果Fig. 1 Tracking results of different kernel filters

在組合核學習中，文獻[22-23]采用高斯核和多項式核組合學習增強全局泛化能力；文獻[24]采用線性核和高斯核進行差異化學習，而在跟蹤場景中，更重要的是判別性或差異化的互補學習，因此本文采用線性核和高斯核進行學習。由于線性核是全局核，可以表征特征空間的全局特性，而高斯核是局部核，具有較強的學習能力，可以表征特征空間的局部特性，因此這兩種核函數進行組合，使得特征空間既具有較好的學習能力，又具有較強的泛化能力。由于多項式核沒有高斯核的學習能力強，故不采用多項式核進行組合學習。

1.2 自適應更新率

在快速檢測得到新的目標區域后，就可以對濾波器進行更新，更新方法如式(10)：

F(α)t=(1-η)F(α)t-1+ηF(α)

(10)

其中η為學習更新率。在KCF跟蹤算法中，學習更新率是一個固定值，不具有復雜場景的自適應性，本文提出利用極大響應值衡量被跟蹤目標的場景置信度。規范化后的極大響應值M-norm為：

M-norm=(Mmax-μ)/(3*σ)

(11)

其中：Mmax為當前幀的極大響應值；μ為歷史幀的極大響應均值；σ表示歷史幀的響應方差。根據3σ原則M-norm基本上為-1到1之間的數，從而可以進一步分析分類器的置信度。

Faceocc1在遮擋環境下的極大響應值和M-norm變化如圖2所示。圖2(a)為無遮擋場景，圖2(d)為圖2(a)的對應響應圖，其極大值Mmax為0.28，M-norm為0.54；當發生輕微遮擋時，圖2(e)為圖2(b)的響應圖，其極大值Mmax為0.268，而M-norm為0.274；在嚴重遮擋時，圖2(f)為圖2(c)的響應圖，其極大值Mmax為0.251，而M-norm為0.181。可見M-norm靈敏地反映了遮擋環境中的分類器對當前目標的置信度水平,M-norm值越大說明分類器性能較高，應該及時更新；值越小，說明分類器受到干擾越大(例如遮擋)，應該減少更新。為了進一步規范化，將M-norm進行平移和歸一化后可得：

(12)

p即為置信度水平，因此，根據置信度水平p設置學習更新率η為：

(13)

當p小于某個閾值Th0時，說明分類器受到干擾較大，應該減小更新率，因此設置一個較小的更新率u0，本文設為0.15；否則，應該增加更新率，以β*p作為更新率，β是一個基準更新率，與KCF算法更新率一致，設為0.02，其中Th0設為0.075。實驗分析表明，KCF算法的更新率在0.02左右達到最優，而本文算法采用了組合核算法，更新率在0.18左右最佳，因此本文將基準更新率β設為0.02。三種更新率(本文自適應更新率,更新率為0.02,更新率為0.015)的tiger2的跟蹤結果如圖3所示。由圖3可知，第124幀時，本文自適應更新率具有最佳的跟蹤性能，明顯優于其他兩種固定更新率。式(13)實質是根據規范化極大響應值M-norm自適應調整濾波器更新率，使其具有場景的自適應性。

圖2 遮擋環境極大響應值Mmax和M-norm變化Fig. 2 Changes of maximum response value Mmax and M-norm in occlusion environment

圖3 tiger2在不同更新率下的跟蹤結果Fig. 3 Tracking results for tiger2 with different update rates

1.3 尺度濾波器估計

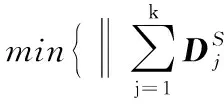
(14)

式中g為1維高斯分布特征。hj在傅里葉變換域的解為：

(15)

(16)

(17)

(18)

其中η0為學習率。

1.4 算法描述

本文算法將目標跟蹤分解為平移和尺度估計兩個獨立的子任務，其中平移濾波器采用了自適應的組合核相關濾波器，圖4為自適應組合核(SACK)跟蹤算法流程，算法描述如下。

算法1 SACK算法。

Translation estimation:

1)根據第t幀視頻序列的位置(xt-1,yt-1)和尺度st-1，提取被跟蹤目標的HOG特征和灰度特征。

2)分別計算線性核和高斯核的相應圖，根據式(9)求解兩種核相關矩陣的最優權重系數b。

3)根據式(4)計算平移濾波器。

4)根據式(6)的響應值極大值，并計算新的位置(xt,yt)。

5)根據式(13)計算自適應更新率η。

Scale estimation:

6)根據第t幀視頻序列的新位置(xt,yt)和尺度st-1提取HOG特征。

7)根據式(15)計算尺度濾波器。

8)根據式(16) 計算最佳估計尺度。

Model update:

9)根據式(10)更新平移濾波器αt。

2 實驗結果與分析

式(1)的正則項參數λ設為0.01；式(5)中高斯核的標準差σ設為0.5，線性核不需要設置參數；式(13)中的閾值Th0設為0.75，u0設為0.15，β設為0.02；式(14)的正則項參數λ設為0.01，其中一維高斯分布g的標準差設為0.25，尺度搜索空間為33個尺度，尺度步長設為1.03；式(17)～(18)中η0設為0.02。測試硬件平臺的配置為Intel I5-3210 2.50 GHz CPU 和4 GB 內存，實驗平臺為Matlab 2013。

2.1 自適應組合核算法的有效性測試

為了測試自適應組合核的有效性，從OTB-50數據集選取了5個視頻序列測試，為了降低尺度對算法的影響，這些視頻序列均沒有尺度變化，本文SACK算法和KCF算法的成功率性能比較如表1所示。為了具有可比性，算法均采用HOG特征，其中：KCF_gauss為高斯核，KCF_poly為多項式核，KCF_linear為線性核(即DCF跟蹤算法)；另外，將KCF_gauss和KCF_linear的核相關函數進行簡單組合，權重b設為0.5，即具有相同權重。

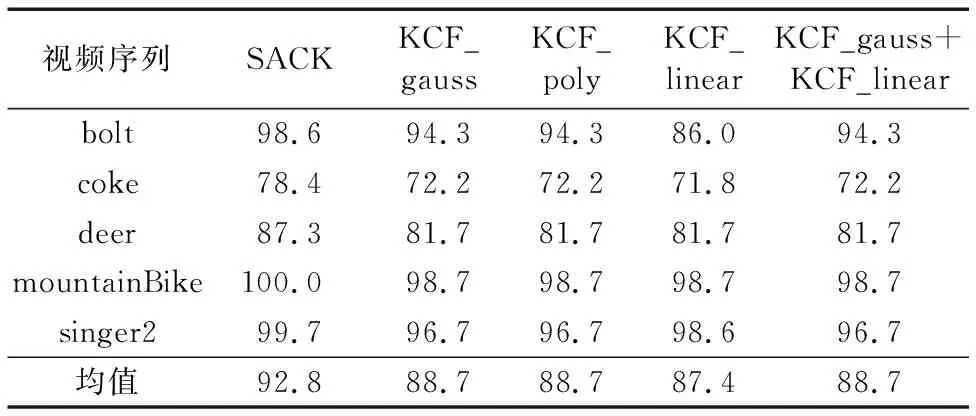
表1 SACK算法與KCF算法成功率對比 %Tab. 1 Success rate comparison of SACK algorithm and KCF algorithm %

由表1可知，本文SACK算法在5個視頻序列中的成功率明顯高于單核算法及KCF_gauss+ KCF_linear組合算法；由于高斯核和多項式核均是全局核，具有相同的泛化能力，因此其成功率基本一致。在bolt視頻序列中，KCF_gauss和KCF_poly成功率均為94.3%，KCF_linear的成功率為86%，KCF_gauss+ KCF_linear 組合算法的成功率為94.3%，可見在bolt視頻序列中，線性核性能略低于高斯核和多項式核，而KCF_gauss+KCF_linear 簡單組合算法沒有提高算法性能，而本文算法在一定程度上提高了跟蹤成功率。KCF_linear在coke視頻序列上的成功率低于KCF_gauss和KCF_poly方法，但在singer2視頻序列上要優于高斯核和多項式核，這體現了不同核的差異性，正是這種核函數的差異性，組合后可以進行互補。本文選取全局核時采用了高斯核，主要是考慮高斯核具有較強的魯棒性[12]。

另外，由表1可知，KCF_gauss+KCF_linear的簡單組合策略并不能顯著提高算法性能，而本文提出的自適應組合策略顯然要優于這種簡單組合策略。本文自適應組合策略不僅考慮了多核響應的整體風險泛函最小，同時考慮了極大響應值的風險，因此具有較好的跟蹤性能。

2.2 復雜場景定量分析

為了驗證跟蹤的有效性，實驗選取10個挑戰性的視頻序列進行定量分析，這些視頻序列具有復雜的場景變化，如光照變化、遮擋、旋轉和尺度等，可以方便地分析各個視頻目標跟蹤算法受不同因素的干擾程度。本文選擇了9個前沿算法與SACK算法比較，包括：雙向尺度估計跟蹤(Bidirectional Scale Estimation Tracker, BSET)算法[26]、DSST[7]、KCF[12]、Struck[27]、跟蹤學習檢測(Tracking-Learning-Detection, TLD)算法[28]、局部無序跟蹤(Locally Orderless Tracking, LOT)[29]、壓縮跟蹤(Compressive Tracking, CT)算法[30]、局部敏感直方圖跟蹤(Locality Sensitive Histograms Tracking, LSHT)算法[31]和顏色命名(Color Names, CN)特征跟蹤算法[32]。10個算法成功率分析結果如表2所示。由表2可知，在所有視頻的比較中，KCF成功率均值為65.8%，BSET成功率均值為59.5%，而本文SACK算法成功率均值為88.7%，明顯高于BSET算法和KCF跟蹤算法。10個算法的平均中心誤差如表3所示，其中：SACK算法的平均中心誤差均值最低為9.1像素，KCF平均中心誤差均值為24.1像素，BSET平均中心誤差均值為44.1像素，可知 SACK跟蹤算法具有最高的平均成功率和最低的平均中心誤差。由于本文提出的自適應組合核方法，不僅繼承了局部核的學習能力，也融入了全局核的泛化能力，而核相關函數在自適應組合的過程中，不是簡單組合而是根據核響應圖及極大響應值的自適應調整，因此具有優良的跟蹤性能。

表2 不同算法在平移數據集上的成功率 %Tab. 2 Success rates of different algorithms for translation dataset %

表3 不同算法在平移數據集上的中心位置誤差 像素Tab. 3 Center location errors of different algorithms for translation dataset pixel

2.3 OTB-50數據集綜合測試

為了全面評測本文算法，利用OTB-50數據集進行了總體性能測試。該數據集共有50個視頻序列(51個被跟蹤目標)，這些視頻序列分別存在著一些復雜的場景變化，例如遮擋、旋轉和背景干擾等，可以方便地分析各個視頻目標受不同因素的干擾程度。本文利用成功率圖和精度圖[21]作為評價標準，10個算法的成功率圖和精度圖如圖4所示。

圖4 OTB-50數據集的精度圖和成功率圖Fig. 4 Precision plots and success rate plots on data set of OTB-50

由圖4(a)的精度圖可知，SACK算法得分最高為0.781，比BSET算法高出3.2個百分點，比KCF跟蹤算法高出4.1個百分點；同時,由4(b)的成功率圖可知，SACK得分為0.582，高于KCF算法6.8個百分點，高于BSET算法2個百分點。因此本文提出的SACK跟蹤算法在OTB-50數據集上優于其他算法。

各算法在形變、遮擋、平面外旋轉和背景干擾等挑戰性屬性集上的成功率圖和精度圖如圖5所示,其中存在形變、遮擋、平面外旋轉和背景干擾的視頻數量分別為19、29、39、21。

由圖5可知，在形變屬性視頻序列(deformation)中，本文提出的SACK算法具有較高的成功率，得分為0.621，而KCF跟蹤算法為0.534，顯著高于KCF算法；同時在精度圖上，SACK算法得分為0.834，而KCF跟蹤算法為0.740。因此，本文算法在形變屬性集上明顯優于KCF算法以及其他算法。另外，由遮擋、平面外旋轉和背景干擾等屬性集上的成功率和精度圖可知，本文算法也優于BSET、DSST和KCF等其他算法。由于本文算法根據被跟蹤目標自適應調整濾波器更新率，使其具有場景的自適應性，因此針對背景干擾具有一定的魯棒性。

不同算法在5個挑戰性視頻上的跟蹤結果如圖6所示，這些視頻序列不同程度地存在著背景干擾、形變、尺度變化和遮擋等現象，同時將本文SACK算法與4種前沿算法進行了分析和比較，包括KCF、DSST、BSET和LSHT算法。

在carScale視頻中，第54幀和第175幀時不同算法沒有明顯的差異，而第225幀時SACK算法跟蹤效果顯著優于DSST和BSET算法，因此SACK算法不僅具有準確的尺度估計能力，而且針對部分遮擋(如視頻中的樹木)有較好的抗干擾能力。在david3視頻中，明顯存在背景干擾，在233幀時只有SACK和KCF算法能有效跟蹤到目標，同時SACK算法的準確性要優于KCF算法。在fleetface視頻中，第647幀時目標出現了平面旋轉等問題，而SACK算法依然能夠有效跟蹤到目標，優于其他算法。在jogging-1視頻中，在第101幀時SACK和LSHT算法能夠準確跟蹤到目標，由于柱子的全局遮擋，其他算法跟蹤失敗；在192幀時，目標出現顯著的形變，SACK算法明顯優于LSHT算法，因此SACK算法針對形變具有較強的魯棒性。在tiger2視頻中，第109和296幀時，僅SACK算法能夠有效跟蹤到目標，而其他算法均出現了“漂移”現象。

另外，本文算法在OTB-50上的處理速度為平均每秒18.9幀，基本上滿足實時跟蹤的需求。綜上所述，SACK算法與BSET、DSST等其他算法相比，具有較明顯的優勢。

圖5 不同算法在不同屬性下的成功率圖和精度圖Fig. 5 Success rate plots and precision plots of different attributes on data set of OTB-50

圖6 不同算法的跟蹤結果對比Fig. 6 Comparison of tracking results of different algorithms

3 結語

本文提出了自適應組合核的魯棒跟蹤算法，該算法包括兩個自適應性：一是自適應組合核策略，根據線性核和高斯核的響應值，自適應調整不同核相關矩陣的權重，不僅考慮了多核響應的整體經驗風險泛函最小，同時考慮了極大響應值的風險泛函；二是根據目標的極大響應值，針對核濾波器設置自適應更新率。本文算法為組合核相關濾波器提供了新的最小風險泛函策略，為相關濾波器融合算法提供了可借鑒的策略和方法。針對OTB-50數據集的實驗結果表明，與BSET、DSST以及KCF等前沿算法相比，本文算法具有較高的成功率和精確度。但本文算法僅利用了HOG特征和灰度特征跟蹤目標，下一步我們將研究深度特征和自適應組合核的跟蹤算法。