基于尾軸-油膜-艉部結構的軸系穩定時間

陳天然， 董良雄， 俞嘉陽

(浙江海洋大學 港航與交通運輸工程學院， 浙江 舟山316022)

0 引 言

航行中的船舶受惡劣環境影響，船體在外力作用下會產生不均勻變形與隨機運動，造成船體形變，軸系、尾軸承油膜與船體之間相互耦合、相互影響，從而使軸系進入不穩定狀態。抑制或削弱船舶軸系振動是加強其工作穩定性和改善傳動性能的關鍵所在。本文應用數值計算，研究了不同載荷、不同轉速下船舶軸系穩定性的變化規律，分析其縱向振動的特性并尋求有效方法，以達到縮短碰摩發生后軸系恢復穩定所用時間的目的，希望為船舶建造的優化設計與軸系的合理安裝提供一定的理論基礎，加強船舶在航行過程中的安全保障。

1 船舶尾軸在外力作用下的穩定性分析

針對船舶尾軸的復雜受力狀態，開展其軸心軌跡的瞬變及由瞬變到穩定過程的研究具有重要理論意義和應用價值。船舶尾軸承承受的動載荷形式有2種：一種是沖擊載荷，其特點是持續時間非常短暫，能量釋放和傳遞是驟然完成的，在沖擊載荷作用下，系統產生瞬態運動，軸心位移發生較大變化；另一種是周期變化的動載荷，最常見的就是碰摩載荷，在其作用下，軸心軌跡發生渦動，軸心軌跡周期變化，軸心軌跡是滑動軸承內部潤滑規律的外部表征，是軸承工作狀態的綜合反映。因此，通過軸心軌跡，可以判斷軸承的穩定性，確定軸承的承載能力，判斷軸承設計參數的合理性。

按照離散化建模思路，首先將船體艉部結構離散化，使離散化的艉部結構之間具有線性彈性聯接，并將尾軸系統簡化為單圓盤系統，兩端由滑動軸承支撐，建立相應的力學模型[1-3]。繪制的力學模型如圖1所示。

具體參數的取值為：m1=100kg；m2=80kg；m3=m4=m5=200kg；c1=c2=c3=5 000N·s/m；k1=k2=5×106；c=0.2mm；r=0.06mm；f=0.1；k3=k4=k5=5×107。

圖1 數值模型結構

設系統的質量矩陣、阻尼矩陣、陀螺力矩矩陣和剛度矩陣分別為M、C、J和K，轉子系統動力學方程為

(1)

2 沖擊載荷下尾軸由擾動到穩定的過程模擬

在正常工況下，軸心軌跡對轉速的變化最為敏感，不同轉速下軸心軌跡在收斂與發散間變化不定[4-6]。在軸系軌跡是收斂的情況下，發生擾動時，軸心軌跡趨向偏離原來的運動軌跡，一段時間后恢復到穩定狀態。在不同擾動下，軸心軌跡恢復的過程和時間都不相同。本文主要分析2種情況下軸心軌跡的變化規律：一種是在沖擊載荷工況時不同轉速下軸心軌跡的變化；另一種是轉子系統存在碰摩載荷工況時，不同轉速下軸心軌跡的變化規律。

船舶在航行過程中，螺旋槳和船體受外力作用，常常會對尾軸的運動造成影響，這種影響作用可用沖擊載荷來進行描述。沖擊載荷作用于軸的矩形脈沖載荷隨無量綱時間的變化規律如圖2所示。沖擊載荷可用式(2)來描述。

圖2 沖擊載荷圖

(2)

在推進軸系的運動過程中，隨著激勵頻率的增大，系統呈現出由穩定運動過渡到周期運動再到混沌運動的狀態，振動系統拓撲結構也會發生相應的改變。本文選取2種軸系工況，即周期運動和混沌運動2種不同轉速工況，對應的轉速分別為760 r/min和800 r/min，進行分析與模擬，得到其振動軌跡曲線和振幅-時間響應曲線如圖3所示。其中，轉速為760 r/min時的軸心軌跡如圖3a)所示，軸頸振動響應如圖3b)、圖3c)所示(其中箭頭線段表示受到沖擊載荷后軸系恢復穩定所需的時間)。

圖3 轉速760 r/min、800 r/min時軸頸振動響應及軸心軌跡圖

由圖3分析得出，沖擊載荷對軸心軌跡產生一定的擾動影響，且沖擊載荷愈強激起的軸系振幅愈大持續時間愈久。轉速為760 r/min時的穩定時間為1.2 s，轉速為800 r/min時的穩定時間為1.4 s，因此，受到同樣沖擊載荷時，選擇合適的轉速可有效縮短軸系受到沖擊后的穩定時間。

改變沖擊載荷的大小和持續時間，保持軸系轉速不變測取尾軸的穩定時間如表1所示。

3 碰摩載荷下的尾軸穩定過程分析

3.1 碰摩載荷下軸心穩定過程模擬

碰摩載荷是船舶營運過程中尾軸與尾軸承發生接觸而產生的一種工況。發生碰摩時，尾軸與尾軸承之間既有碰撞產生的徑向沖擊力，也有軸向摩擦力，該作用力由尾軸承來承受。假設尾軸與尾軸承之間的間隙為δ，碰撞過程為彈性變形，則碰摩力可表示為

(3)

同樣，取碰摩摩擦因數為0.1，間隙δ為0.000 2，即保持碰摩載荷的大小不變且作用時間相同，且碰摩裝置剛度一定，改變軸系轉速，當軸系轉速分別為760r/min、800r/min時，測得不同轉速條件下軸系恢復穩定所需時間的曲線，結果如圖4所示，其中圖4a)為轉速760r/min時的軸心軌跡圖，圖4b)和圖4c)分別為2種轉速下的振動時程圖。

圖4 轉速為760 r/min、800 r/min，碰摩摩擦因數為0.1，碰摩間隙為0.000 2時軸心軌跡圖與軸頸振動響應圖

從圖4可看出：當船舶軸系碰摩載荷大小和彈簧剛度一定時，船舶軸系轉速的改變會對其軸心軌跡的穩定造成一定影響。隨著軸系轉速的提高,軸承支承油膜力動態特性發生改變,軸系在碰摩載荷作用下引起的擾動振幅較大,振動幅值由小到大,從不碰摩到輕微碰摩,從輕微碰摩到比較嚴重的碰摩。

另外，碰摩摩擦因數的改變對軸系振動也有一定影響，但不如另外2個參數明顯。若碰摩摩擦因數越大，即彈簧剛度越大，則軸系發生碰摩后的縱向振動越劇烈，轉子振幅變化越大且曲線變得更不光滑，故在受到同樣的碰摩載荷時，適當地調節轉速和選擇恰當的摩擦因數可有效縮短軸系穩定時間。

3.2 碰摩載荷下的尾軸穩定性比較

為進一步對碰摩載荷作用下尾軸的穩定性進行比較，保持軸系轉速不變，通過改變碰摩載荷的摩擦因數和彈性系數，觀察穩定時間并進行比較。記錄穩定時間并計入表2。

表1 760 r/min時不同載荷下的穩定時間 s

表2 500 r/min時不同載荷下的穩定時間 s

表2的數據可以制作成圖5、圖6。

圖5 穩定時間隨彈性系數的變化曲線

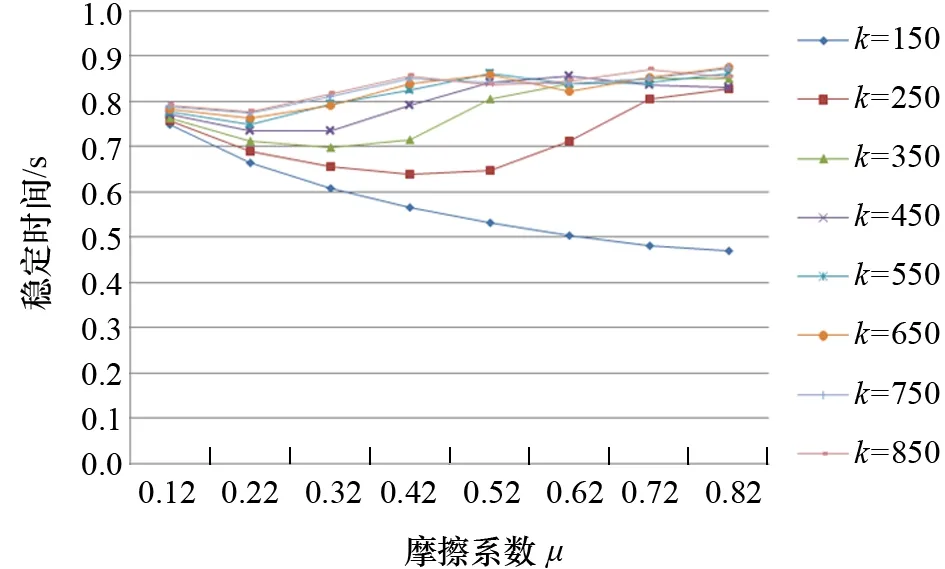
圖6 穩定時間隨摩擦因數的變化曲線

圖5是摩擦因數一定，穩定時間隨彈性系數的變化曲線。圖中x軸為彈性系數，不同標記的折線表示各摩擦因數下的變化趨勢。由圖5可知，在相同的摩擦因數下，當軸系的彈性系數不同時，軸系恢復穩定所需時間呈現不同的變化特性。

圖6是彈性系數一定，隨著摩擦因數的增大，穩定時間的變化曲線，可看出在不同摩擦因數下穩定時間增速不同，摩擦因數越低，穩定時間增速越小，甚至呈上升趨勢。例如,彈性系數為150時恢復速度最快，曲線最光滑。當摩擦因數較小時，彈性系數較低則軸系恢復穩定所需時間較大；當摩擦因數較大時，彈性系數越高則軸系恢復穩定所需時間越大。

4 結 論

本文以船舶尾軸為研究對象，建立尾軸-油膜-艉部結構系統動力學模型，研究發生沖擊和碰摩之后的穩定性特征,為碰摩發生后軸系的安全評估提供一定的理論參考。

(1) 沖擊和碰摩載荷都會對船舶推進軸系軸心運動產生擾動，從而影響其穩定性，影響程度與軸心轉速有關。在軸心軌跡處于非周期運動區域內,載荷影響時間長,振幅衰減慢, 軸系恢復穩定狀態的能力弱。

在周期運動區域,碰摩響應衰減快,而且軸的轉速偏離該頻率區域越遠,碰摩響應振幅衰減越快，軸系恢復穩定狀態的能力越強。

(2) 相對于沖擊載荷,碰摩載荷發生后軸系恢復穩定所需的時間短。在碰摩載荷的作用下，一方面可通過調節軸系的工作速度能夠回避碰摩作用對軸系的破壞作用；另一方面，發生碰摩時，合適的摩擦因數也會縮短尾軸的穩定時間，從而在一定程度上加強了船舶軸系保持穩定的能力。