基于剛柔耦合的無油渦旋壓縮機小曲拐動力特性分析
彭斌,方圓力,朱永軍
(蘭州理工大學 機電工程學院,甘肅 蘭州 730050)
0 引言
無油渦旋壓縮機作為最新一代的容積式壓縮機,具有可靠性高、結構簡單、噪聲小、振動低、效率高的特點。傳統多體系統動力學的研究主要局限于剛體領域,隨著現代機械向高精度、高速度以及高效率的方向發展,純剛性假設已很難滿足某些條件下的精度要求。因此系統自身的剛性運動與系統自身的變形耦合產生的彈性力學問題逐漸成為當代研究的熱點。無油渦旋壓縮機是一種高速運轉的機械,僅僅依靠純剛體系統無法完全體現渦旋壓縮機準確的運動狀況。作用在動盤上的切向力會使動盤產生繞主軸偏心線轉動的自轉力矩,使動、靜盤不能正常嚙合,在設計中往往需要采用防自轉機構來限制此自轉力矩。無油渦旋壓縮機采用小曲拐作為防自轉機構,其動力特性將直接關系到防自轉機構能否很好地平衡自轉力矩[1-2]。
余洋通過模擬仿真得出了運動間隙對動態特性的影響[3];張春、黃華軍等人建立了剛柔耦合仿真模型,對轉子系統軸承進行了力學分析[4];邵兵通過對渦旋壓縮機整機的仿真分析,得出了氣體力對整機泄漏的影響[5]。彭斌等對無油渦旋壓縮機的前景進行了展望[6],王志軍利用三維軟件對實際運動進行了仿真,并對實際運動與理論運動進行了比對分析[7]。
因此,小曲拐作為渦旋壓縮機高速運轉的零件,其動力特性的研究具有重要的意義。本文通過Ansys與Adams的聯合仿真,建立了渦旋壓縮機小曲拐的剛柔耦合模型,并對其進行了仿真分析,得到的結果將對小曲拐的優化提供重要的依據。
1 小曲拐的機構模型
圖1所示為小曲拐裝配圖。3個小曲拐兩端的軸頸分別插在動盤與機架中。
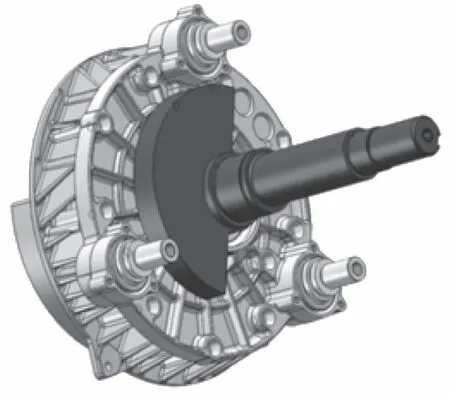
圖1 小曲拐裝配圖
圖2所示為小曲拐四桿機構模型,其中1為連接電動機的偏心主軸,3、4、5為3個小曲拐,6為機架,2為連接偏心主軸與小曲拐的動盤。機構有5個活動構件,8個旋轉副,其中有2個虛約束,則需要去掉虛約束,由此得到的機構的自由度計算公式為:
F=3n-(2p1+Ph)=3×3-(2×4+0)=1
(1)
其自由度為1,保證了小曲拐的正常運動,從小曲拐四桿機構可以看出3個小曲拐的運動規律一致,且與偏心主軸的運動一致,使得動盤公轉運動而不發生自轉,因此滿足渦旋壓縮機防自轉的要求。
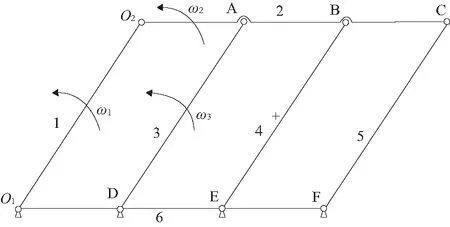
圖2 小曲拐四桿機構模型
2 柔性化理論
Adams柔性體所用的理論為柔性化理論,柔性體的坐標系如圖3所示,包括動坐標系ed以及慣性坐標系er。動坐標系是為了研究柔性體而建立的坐標系。慣性坐標系相當于大地坐標系,它不會隨時間的變化而變化,而動坐標系可以相對于慣性坐標系在一定范圍內移動與轉動,動坐標系在慣性坐標系中的坐標則被稱為參考坐標系[8]。
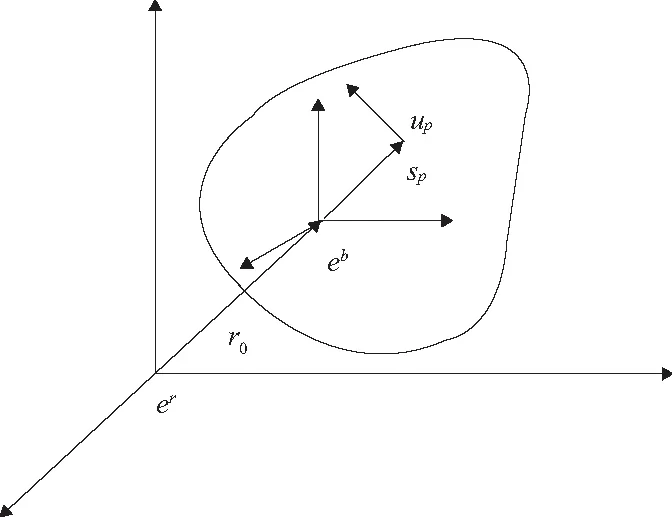
圖3 柔性體節點坐標
對于柔性體上的任意一點p,其位置向量為:
(2)

柔性體中的任一節點采用模態(模態為一個構件的固有屬性)坐標的方式來表示變形:
(3)
式中:φp為p點的里茲基向量變形的模態矩陣;qf為廣義坐標系。
3 剛柔耦合模型的建立
3.1 MNF文件的建立
利用SolidWorks建立小曲拐的三維模型,通過parasolid通用格式導入到Ansys中建立渦旋壓縮機的虛擬樣機模型,建立的虛擬樣機模型如圖4所示。

圖4 虛擬樣機模型
定義小曲拐的材料屬性,彈性模量為210GPa,泊松比0.3,密度7.8×103kg/m3,定義單元類型為solid187格式,最后進行網格的劃分。由于小曲拐前后軸頸都插在軸承中,因此,在小軸的軸頸部分建立剛性區域,建立的有限元模型如圖5所示,最后將生成的MNF文件導出,模型節點數為14 791,單元數為77 850。

圖5 小曲拐有限元模型
3.2 約束與驅動的添加
Bushing軸套力是通過一種數學模型的方式,利用軟件設置彈性和阻尼來模擬幾個零件之間的連接關系,通過設置Bushing徑向剛度、軸向剛度和角剛度的數值來模擬軸承。由于軸承的阻尼很小,因此在本章中忽略不計。根據軸承類型選取位移剛度數值為Kx=1.84e5、Ky=1.84e5、Kz=2.6e5,選取的角度剛度數值為Kxx=1.4e5、Kyy=1.4e5、Kzz=0[9]。
在渦旋壓縮機虛擬樣機模型建立之后,通過各零件之間關系對渦旋壓縮機各個零件添加約束關系及驅動,按電動機的額定轉速設置主軸的轉速為1 440r/min。各個零件之間的約束如表1所示[10]。
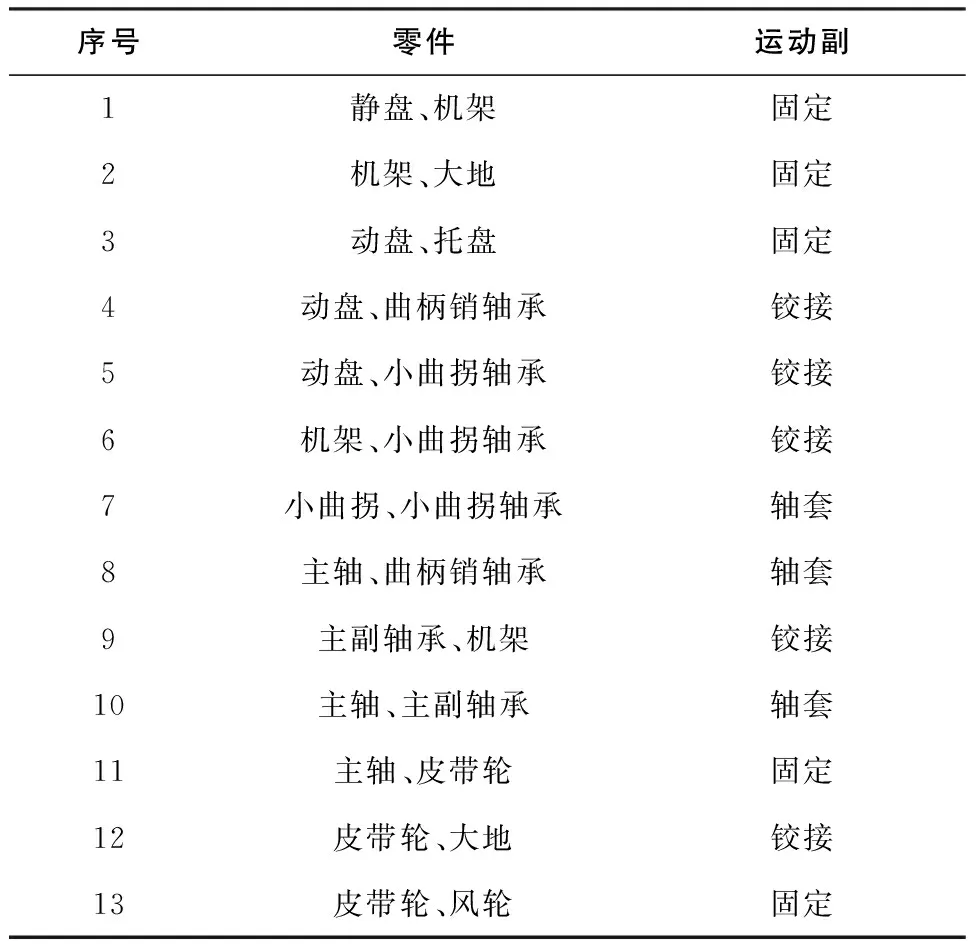
表1 渦旋壓縮機剛柔耦合模型各零件間關系
3.3 虛擬樣機的裝配
在Adams中,根據上面的各零件之間的關系進行渦旋壓縮機的剛柔耦合模型的虛擬裝配,導入MNF文件進行柔性體的替換。圖6為柔性體替換示意圖。
圖6 柔性體替換示意圖
4 剛柔耦合仿真分析
在Adams中添加Adams/Durability模塊,在此模塊中可以分析得出柔性體任意時刻的動態特性,也可查看柔性體上任意一個節點的應力應變隨主軸轉角的變化趨勢。
如圖7-圖9所示的是渦旋壓縮機3個小曲拐在主軸旋轉一周的工作狀況下,10個最大節點的應力值。由圖中看出,最大的應力前7個節點是相同的,由此可知,渦旋壓縮機3個小曲拐的受力情況、運動狀態基本相同,符合小曲拐平面四桿機構的運動規律。
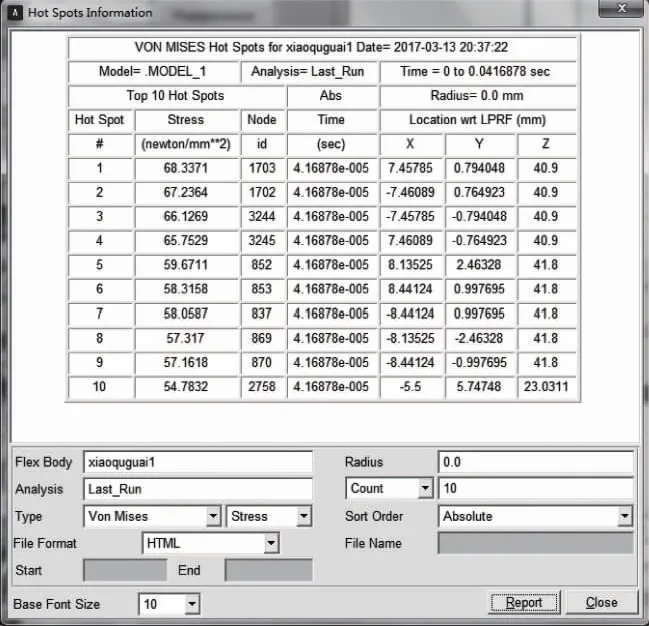
圖7 小曲拐1 10個最大應力點
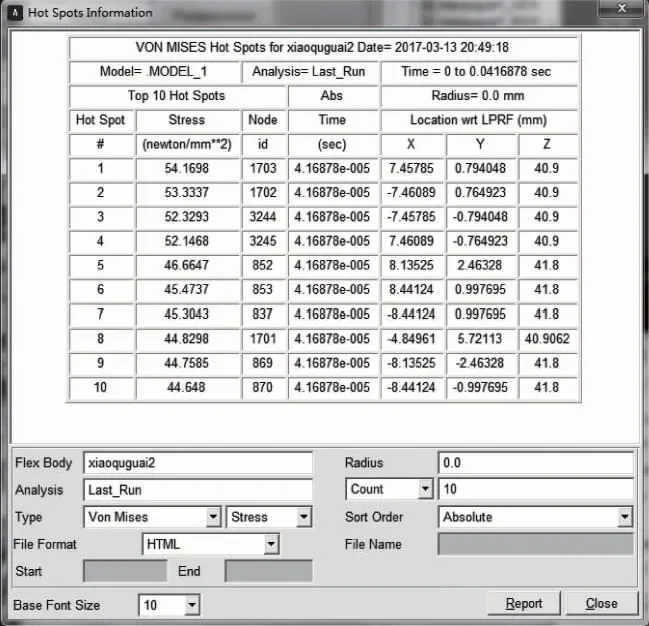
圖8 小曲拐2 10個最大應力點
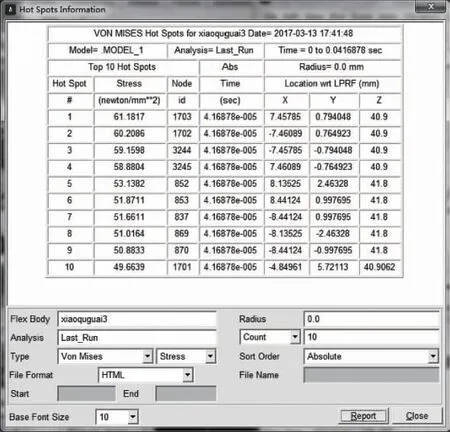
圖9 小曲拐3 10個最大應力點
圖10-圖12所示為3個小曲拐應力應變的等值云圖。小曲拐兩端的軸頸插在軸承之中,因此,小曲拐兩端軸頸的應力應變很小。從圖中可以看出小曲拐的發生最大應力、應變的位置在小曲拐退刀槽附近,兩端的軸頸應力應變很小,符合之前小曲拐剛性區域的建立。

圖10 小曲拐1應力與應變等值云圖
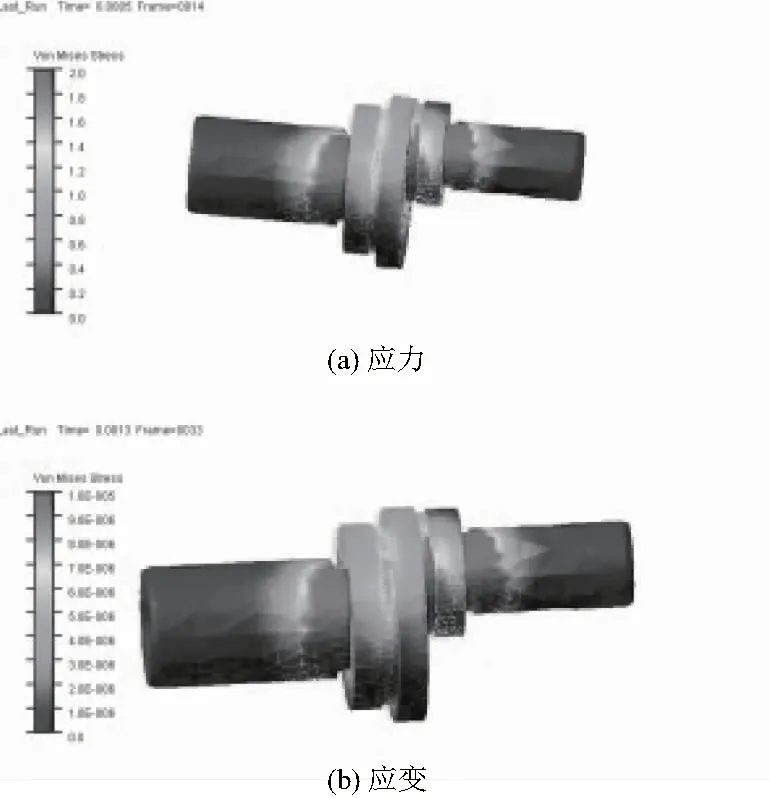
圖11 小曲拐2應力與應變等值云圖

圖12 小曲拐3應力與應變等值云圖
圖13-圖15所示的是小曲拐應力、應變最大的節點1 703(從圖7-圖9可以看出3個小曲拐的發生最大應力、應變的節點編號均為1 703)的應力、應變隨主軸轉動一周的變化情況。由圖中可以看出,3個小曲拐應力應變的變化規律基本一致,進一步說明了渦旋壓縮機3個小曲拐受力情況與運動規律基本相同,符合小曲拐平面四桿機構的運動規律。由于渦旋壓縮機電動機剛開始驅動,因此圖中剛開始會出現一個突變狀況,由圖中看出3個小曲拐的最大應力約為11N/mm2,而最大應變約為7×10-5mm。由此可見,小曲拐的變形還很小的,因此選擇的小曲拐符合渦旋壓縮機防自轉的要求,并為小曲拐的進一步優化設計提供重要的參考。

圖13 小曲拐1最大應力點應力與應變
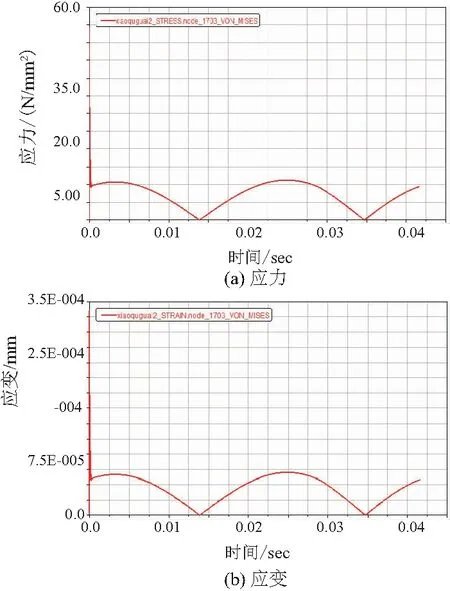
圖14 小曲拐2最大應力點應力與應變


圖15 小曲拐3最大應力點應力與應變
5 結語
1) 利用Ansys與Adams聯合仿真,建立了渦旋壓縮機的剛柔耦合模型。
2) 通過小曲拐應力最大的10個節點可以看出:3個小曲拐應力最大的前7個節點是相同的。
3) 通過應力應變等值云圖中可以看出小曲拐最大變形位置在退刀槽附近。
4) 通過小曲拐最大節點應力應變的變化趨勢得知3個小曲拐有相似的運動規律與受力狀況。符合小曲拐平面四桿機構的運動規律,為小曲拐進一步的優化提供重要的參考。

