四足機器人斜面運動規劃及控制研究
杜威,楊忠,許昌亮,張輝斌
(南京航空航天大學 自動化學院,江蘇 南京 210016)
0 引言
四足機器人(quadrupedrobot,QR)屬于足式機器人,相對于履帶式和輪式機器人,具有機動性好、環境破壞程度小、主動隔振等優點,應用前景良好。該型機器人涉及力學、機械學、生物學、計算機、人工智能等多學科,相關技術一直是國內外機器人領域研究的熱點之一。以美國卡耐基梅隆大學的波士頓動力實驗室為代表,2005年發布了BigDog大狗機器人,又先后推出了如AlphaDog、LittleDog、Cheetah等產品,引起行業內的廣泛關注。
能否在不同地形條件下實現平穩運動,是一個機器人是否具有實際使用價值的評判標準。斜面是自然界中常見的地形,一些崎嶇的地形也可以等效為斜面。因此,研究四足機器人在斜面上的運動控制具有重要意義。經典控制和現代控制在設計過程中一般是基于被控對象的精確數學模型。對于四足機器人來說,因其具有非線性、高耦合、模型復雜等特點,采用傳統的控制理論和方法往往存在局限性,難以取得滿意的控制效果[1]。模糊控制是建立在模糊集合論基礎上的一種基于語言規則與模糊推理的控制理論,在控制非線性、高耦合及參數和結構不確定的復雜過程中具有較好的控制效果。
在對四足機器人運動學建模的基礎上,從機身姿態、足端軌跡以及步態周期3個方面分析并設計了四足機器人斜面運動方式,并建立了一種應用于四足機器人斜面運動的模糊控制系統,最后通過仿真實驗證明所設計的控制系統具有較好的控制效果。
1 運動學建模及斜面運動規劃
1.1 運動學建模
四足機器人簡化模型由機身、大腿和小腿等構件組成,構件間由旋轉關節連接,連接部分分別為負責橫向擺動的臀關節、負責上下抬腿的髖關節以及膝關節。臀關節負責內外擺,實現機身左右擺動;髖關節和膝關節分別負責大腿和小腿的抬起和落下,實現機器人前后運動。四足機器人采用內膝肘式設計,以前進方向為基準,將左前腿、左后腿、右前腿以及右后腿分別命名為LF、LH、RF、RH。關節連桿結構見圖1。

圖1 四足機器人的關節連桿結構及坐標系定義
采用D-H參數法[2]確定機器人各構件間的位姿關系。四足機器人的坐標系定義示意如圖1所示。以RH為例,定義世界坐標系{W},機身坐標系{B},以及足端坐標系{E}。同時定義臀關節坐標系{1},髖關節坐標系{2},膝關節坐標系{3},以上3個坐標系坐標原點分別位于3個關節位置,坐標系方向由D-H法規范確定。
基于上述四足機器人的關節連桿結構以及坐標系定義,可從足端坐標系沿各關節連桿依次向機身坐標系進行齊次變換,得到足端坐標系到機身坐標系的轉換矩陣:
Tbe=Ab1A12A23A3e
(1)
式中:Ab1,A12,A23,A3c為坐標系{B}、{1}、{2}、{3}、{E}之間的齊次變換矩陣。由D-H參數可確定上述各矩陣,進一步可以得到:
(2)
式中:si=sinθi,ci=cosθi,sij=sin(θi+θj),cij=cos(θi+θj);l1、l2、l3與θi為圖1中所示的各連桿及對應角度;(a,b,c)為坐標系{1}的坐標原點相對于機身坐標系{B}的位置。下標i、j分別取1、2、3。
由式(2)可以得出:
(3)
(4)
矩陣Rbe反映了足端坐標系到機身坐標系的旋轉關系,三維矢量Pbe反映了足端在機身坐標系中與質心的位置關系,兩者共同體現了機器人足端的位姿。
1.2 斜面運動規劃
斜面運動規劃的關鍵是保證四足機器人在行走過程中的穩定性。四足機器人本身具有較好的結構穩定性,但在斜面運動過程中,由于受到重力的作用,機體姿態以及運動步態的變化都會對其運動的穩定性造成影響[3]。本節從機體姿態、足端軌跡以及步態周期3個方面對四足機器人的斜面運動規劃進行研究。
四足機器人在斜面運動時的機體姿態一般有水平姿態以及平行于斜面姿態兩種[4],如圖2所示。相對于水平姿態而言,平行于斜面姿態具有前后腿的運動范圍相當、足端軌跡規劃簡單、穩定裕度高等優勢[4],故四足機器人在斜面運動過程中采用平行于斜面姿態。

圖2 四足機器人兩種機體運動姿態
常用的足端軌跡曲線包括拋物線、心形線、擺線等。本文選取一種零沖擊足端軌跡的規劃方法,其具有沖擊小,曲線圓滑,落地角度垂直不易打滑等優點[5],在坐標系{W}下,水平與豎直方向的足端軌跡數學表達式分別如式(5)與式(6)。式中,S為步幅,H為抬腿高度,Tm為擺動相周期。
(5)
(6)
步態選擇方面,選取穩定性高的三角步態作為四足機器人在斜面上的運動步態,并采用LF-RH-RF-LH的腿部運動順序以獲得最優的穩定裕度[6]。本文的運動步態時序圖如圖3所示。其中,黑色矩形表示腿部處于支撐相,白色矩形表示腿部處于擺動相。

圖3 三角步態運動時序
2 斜面運動控制設計
2.1 模糊控制器設計
用模糊控制方法解決控制問題時,重點在于對控制中所可能出現的各種情形加以分析,依據控制者的經驗和先驗知識,尋求解決的一般方法,并用模糊控制規則的形式加以體現,模糊控制的精度將依賴于模糊控制規則制定得是否合理和詳盡[7-8]。
圖4是開環斜面運動過程中的機身滾轉角變化仿真圖。1.3s與2.1s分別是第一個運動周期內RH與LH處于擺動相的時刻,可以看到這兩個時刻的機身滾轉角絕對值較大。觀察機器人的爬坡過程,可以發現RH與LH處于擺動項時,機器人機身會發生明顯傾斜,即RH處于擺動相,機身明顯向右傾;LH處于擺動相,機身明顯向左傾。現做如下處理:若機身右傾,令LH的臀關節角度減少、髖關節角度增加;若機身左傾,令RH的臀關節角度減少、髖關節角度增加。以上操作均可減少機身的滾轉角度絕對值,使機身趨近水平位置。

圖4 開環運動過程的機身滾轉角變化
基于以上分析,設計應用于四足機器人斜面運動的模糊控制系統。確定模糊控制系統為雙輸入四輸出,四足機器人機身的滾轉角(az)以及滾轉角的變化率(wz)作為輸入變量:
az∈X1=[-0.15,0.15] (rad)
wz∈X2=[-1,1] (rad)
LH的臀關節轉動角度和髖關節轉動角度(anglelh1、anglelh2)以及RH的臀關節轉動角度和髖關節轉動角度(anglerh1、anglerh2)作為輸出變量:
模糊控制系統的結構圖如圖5所示。

圖5 模糊控制系統結構
2.2 論域和隸屬度函數選擇
選定滾轉角az的模糊論域AZ={-2,-1,0,1,2};模糊集為{NB,NS,Z,PS,PB},分別對應“負大”、“負小”、“零”、“正小”、“正大”;隸屬度函數種類選擇為“trimf”,如示意圖6所示。wz、anglelh1、anglerh1、anglelh2以及anglerh2的隸屬度函數圖像均與圖6類似,后文僅給出隸屬度函數對應的參數。

圖6 az的隸屬度函數
選定滾轉角wz的模糊論域WZ={-2,-1,0,1,2};模糊集為{NB,NS,Z,PS,PB},分別對應“負大”、“負小”、“零”、“正小”、“正大”;隸屬度函數種類選擇為“trimf”,隸屬度函數參數分別為:[-3, -2, -1] ,[-2, -1, 0] ,[-1, 0 ,1] ,[0, 1, 2] ,[1, 2, 3] 。
anglelh1、anglerh1、anglelh2以及anglerh2四者的論域與隸屬度函數設置相同。對應論域分別為ANGLELH1、ANGLERH1、ANGLELH2、ANGLERH2;論域內容均設置為{0,1,2,3};模糊集為{Z,S,M,B},分別對應“零”、“小”、“中”、“大”;隸屬度函數種類選擇為“trimf”,隸屬度函數參數為[-1, 0, 1] ,[0, 1, 2] ,[1, 2, 3] ,[2, 3, 4] 。
2.3 模糊規則設計
根據2.1節的分析,對于所述雙輸入四輸出的模糊控制器采用以下的條件語句來描述控制規則:
If(Aisa)and(Bisb)then(Cisc)and(Disd)and(Eise)and(Fisf)
對于本文中應用于四足機器人斜面運動的模糊控制器,設計規則如下:
規則1:若四足機器人的滾轉角(az)為正大(PB)且滾轉角的變化率(wz)為正大(PB),則LH的臀關節轉角(anglelh1)為零(Z)且LH的髖關節轉角(anglelh2)為零(Z)且RH的臀關節轉角(anglerh1)為大(B)且RH的髖關節轉角(anglerh2)為大(B)。
依照同樣的方法寫出其他規則,可以得到模糊控制規則表,如表1所示。表中LH1、LH2、RH1、RH2分別表示anglelh1、anglerh1、anglelh2、anglerh2。

表1 模糊控制規則
3 仿真實驗驗證
仿真實驗采用Matlab與Adams的聯合仿真方式[9]。在Adams中建立四足機器人的三維模型,在Matlab中建立四足機器人的控制系統,通過使用Adams/control模塊建立兩者間的數據通信通道。
需要說明的是,為減少Matlab與Adams之間交換的數據量,在聯合仿真過程中僅針對LH與RH的臀關節與髖關節進行數據交互。在開始仿真前,根據第一章規劃的斜面運動方式,預先設計開環狀態下所有關節的運動情況,并通過SPLINE函數導入到Adams模型中的對應關節。仿真開始后,控制器生成的控制信號將會疊加在4個被控關節角之上,形成新的關節角度以驅動模型運動,完成聯合仿真[10]。
四足機器人機身及其他關節連桿的材料均選擇為鋁,密度為2.74e-6kg/mm3。為簡化模型,機身設計為長方體,長為300mm,寬為75mm,高為20mm;大小腿均設計為圓柱體,高為120mm,底面半徑為12.5mm;斜面設計坡度為5°,靜摩擦系數為0.3,動摩擦系數為0.5。運動規劃方面,采用穩定性較高的三角步態,設置步幅為40mm,抬腿高度為50mm,運動周期為1.6s。
圖7為四足機器人在一個運動周期內的行走過程示意圖。圖8為四足機器人分別在開環與模糊控制下運動過程的機身滾轉角變化對比圖。其中,虛線為開環運動狀態下機身滾轉角的變化情況,實線為經模糊控制后機身滾轉角的變化情況。圖9為坐標系下機身質心在斜面運動過程中的運動軌跡,模型運動方向為X軸負方向。

圖7 四足機器人的運動過程
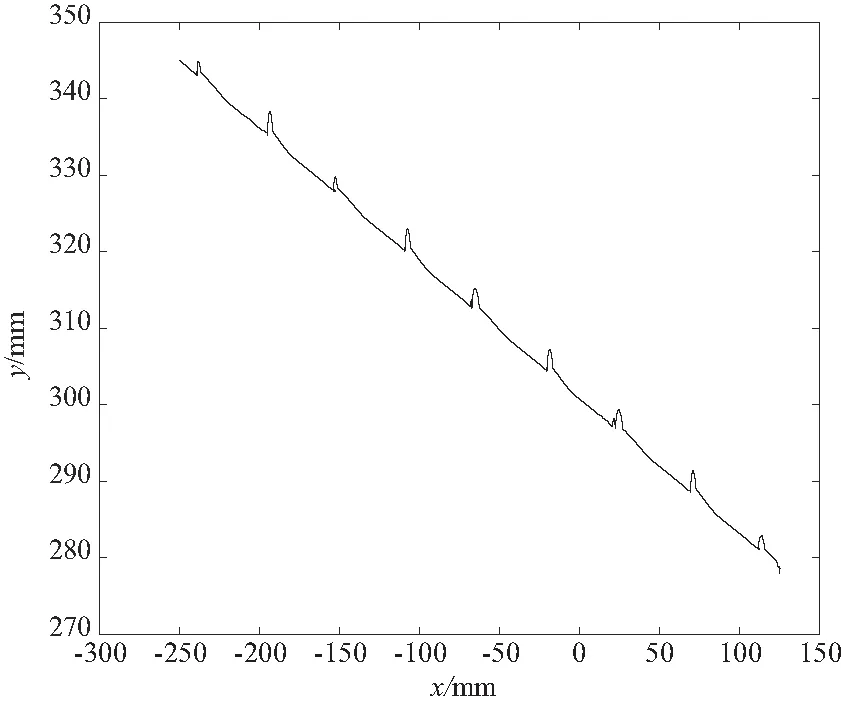
圖9 坐標系下機身質心運動軌跡
4 結語
對四足機器人的斜面運動方式進行規劃,提出了一種應用于四足機器人斜面運動的模糊控制方案。使用Matlab與Adams的聯合仿真進行仿真實驗,證明了所設計的斜面運動規劃滿足四足機器人的正常運動,所設計的模糊控制系統可以有效增加機器人的運動穩定性,達到較好的控制效果。

