計及DG隨機性的配網無功優化與降損策略

王冠翔 ，郭文萍 ，廖敬丹 ，陳國發 ，張永年

（1.國網甘肅省電力公司武威供電公司，武威733000；2.蘭州理工大學 電氣工程與信息工程學院，蘭州730050）

在全球能源危機背景下，世界各國都在開展節能減排和發展可再生能源技術，減小網損是緩解能源危機和實現節能減排的重要手段[1]。由于我國配網尤其是農網存在網架結構薄弱、無功補償設備老化等問題，導致損耗嚴重，因此研究降低配網損耗的措施尤為重要。配網損耗包括兩個方面，即設備損耗和系統運行損耗。采用先進的優化方法，對配電網進行無功優化，是降低電網損耗十分重要和有效的手段。通過合理配置接入配電網中的DG，不僅可以減小系統網損，提高電能質量，還可以提高配電網經濟效益。但DG在電網中的滲透率不斷提高，改變了電網原先潮流分布、配電網形態和結構，使得配電網變得更復雜，協調運行更困難，尤其是DG出力的隨機性和柔性負荷的實時變化都會對配電網的優化結果產生較大影響。傳統的無功優化把DG的出力等價為一個恒定功率輸出的PQ型電源，忽略了分布式電源本身所具有的隨機性，不能很好模擬DG間歇性對配電網的影響，因此傳統無功優化策略不再適用[2]。

目前，針對含DG配電網無功優化問題中，DG和負荷的不確定性及波動性問題，國內外學者展開了大量的工作。文獻[3]將轉換側電流作為限制條件，利用概率論方法分析了風電機組的輸出特性，建立不同場景下含風電機組的配電網無功優化模型，并采用融合了微分進化的細菌群體趨藥性算法，對模型進行求解。文獻[4]針對風機出力的隨機性，提出基于拉丁超立方采樣的Monte Carlo概率潮流計算方法CLMCS（correlation Latin hypercube sampling Monte Carlosimulation），形成風速場景，采用場景縮減技術，得到風機出力的典型場景，將不確定性問題轉化為確定性潮流問題。但以上參考文獻僅考慮了配電網無功優化中風電機組的隨機性問題，但在實際的電網運行中，光伏發電出力與負荷的隨機性同樣會對含DG配電網的無功優化帶來影響。

此外，傳統配電網無功優化大多以網損最小為目標函數建立數學模型，忽略了電網的電能質量。為此，本文在現有文獻的基礎上，考慮電網的電能質量與經濟效益，建立了以有功網損、電壓偏差最小為多目標函數的數學模型。提出一種基于高斯變異和混沌擾動的人工蜂群算法，求取目標函數最優解。該算法在傳統ABC算法的基礎上，引入高斯變異，加強了局部搜索能力，搜索精度更高。加入混沌擾動克服了個體易陷入局部最優的不足，同時提高了算法的魯棒性。最后，在改進的IEEE-33節點配電網系統中，驗證了所提方法的有效性。

1 基于最優場景法多目標優化模型

1.1 Wasserstein距離指標

為了準確實現含DG配電網的無功優化，就不能忽略配電網中DG和負荷的隨機性，所以考慮通過場景法得到DG真實出力的近似值。

Wasserstein概率距離[5]定義為兩個概率分布之間的距離，記作 dw，r：

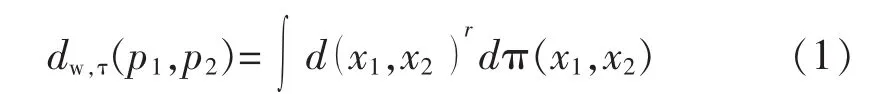
式中：p1和 p2為概率密度函數；π（x1，x2）為聯合概率密度函數；r為階數。因此，保證dw，τ最小，以將離散概率分布，近似轉化為連續分布的近似問題。

根據場景模擬的思想，為獲得最優場景，即使得 Wasserstein 距離 dr（p，）最小，則需要求解概率測度函數的最優分位點zs及對應的概率，其中=上的點質量。

Wasserstein距離指標下的最優分位點zs由下式表示為

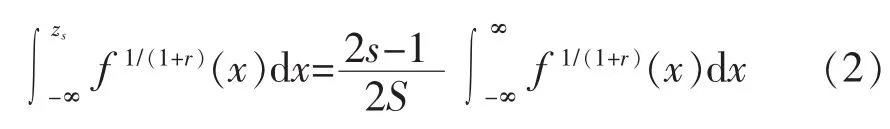
式中：x為一維連續變量，f（x）為x的概率密度函數，S為離散分位點的個數。

分位點zs的概率ps表示為

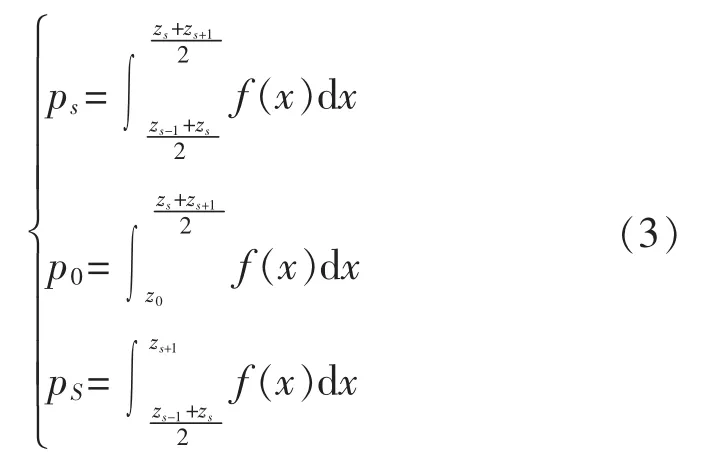
式中：z0=-∞；zs=+∞；s=2，…，S-1

1.2 基于Wasserstein距離的多場景模型

1.2.1 風電機組輸出的最優分位點

風機出力概率密度函數為

其中：

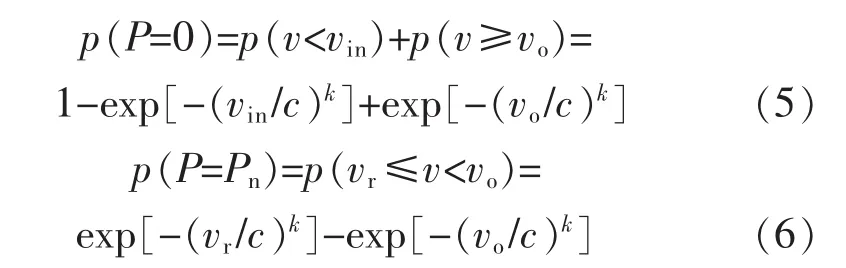
式中：P為風力機組的輸出功率；vin為切入風速；vr為額定風速；vo為切出風速；h=（vr/vin）-1；Pn為風電機組的額定功率；c＞0為概率分布的尺度參數；k＞0為形狀系數。

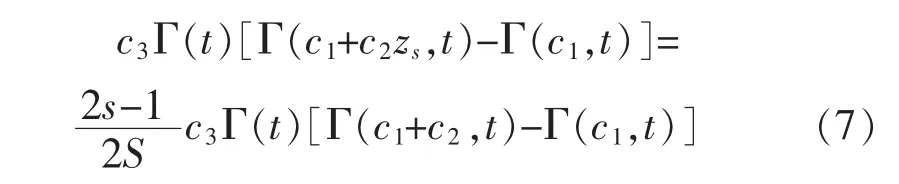
式中：t=（k+r）/［（1+r）k］ 且一般取 r=2，c1=vin/c，c2=（vin/c）/（h/pn），c3=（kc2）-r/（1+r）（1+r）t。

1.2.2 光伏輸出的最優分位點

光伏出力概率密度函數：

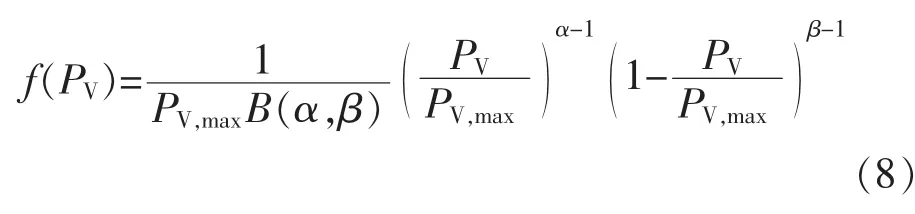
式中：PV，max為最大光伏功率；B（α，β）為 Beta 函數；α、β為Beta分布的形狀參數。

將式（8）代入式（2），得光伏出力離散分位點：

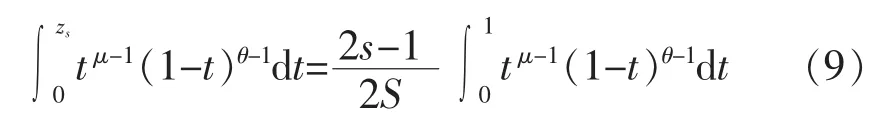
1.2.3 負荷模型

同一地區的負荷因為晝夜與季節等因素，導致隨機性和波動性較強，因此把負荷作為一個隨機變量來考慮，依據以前負荷狀態，對負荷進行預測，采用離散分布近似連續分布。根據負荷預測曲線，將負荷劃分為nd個不同的運行狀態，對應概率為pndd。

1.2.4 多場景模擬

風電、光伏出力和負荷的場景集合δSC，由式（10）表示為[8]

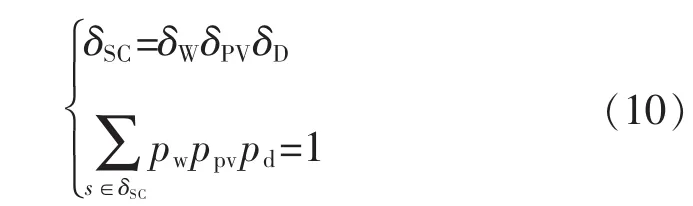
式中：δW、δPV和 δD分別為風電、光伏出力和負荷的離散概率分布集合；pw、ppv和pd分別為風電、光伏出力和負荷在不確定情況下的概率。系統在場景s下的概率：

1.3 目標函數

傳統電力系統配電網無功優化，數學模型多以有功網損最小為目標函數，忽略了電網電能質量，因此本文在網損的基礎上考慮了電壓偏差。

1.3.1 多目標優化模型

（1）有功網損最小

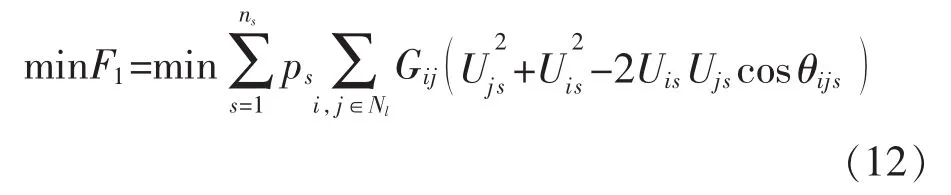
式中：F1為系統有功網損；s表示第s個場景；Gijs為節點i、j之間的電導；θijs為節點i、j之間的電壓相角差；Uis、Ujs分別為節點 i、j的電壓幅值；Nl為網絡輸電線路集合；ns為場景數。

（2）電壓偏差最小

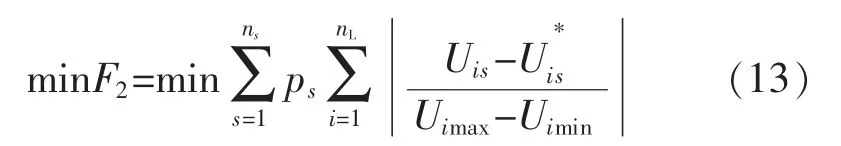
式中：F2為節點電壓偏差；Ui*s為節點i的額定電壓；Uimax、Uimin為節點i的最大、最小允許電壓；NL為系統負荷總節點數。

1.3.2 約束條件

（1）等式約束條件

式（14）為配電網運行的潮流方程：

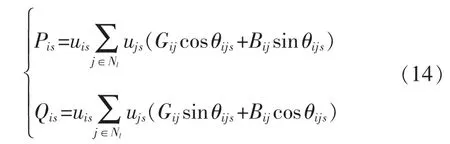
式中：Pis、Qis為節點i注入的有功功率與無功功率；Ni為所有與節點i相連的節點集；Bij為節點i、j之間的電納。

（2）不等式約束條件

節點電壓約束：

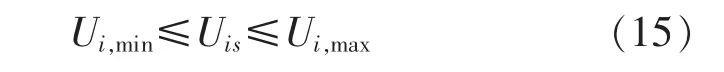
DG輸出有功功率約束：

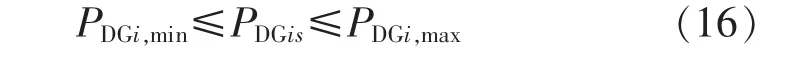
無功補償容量約束：

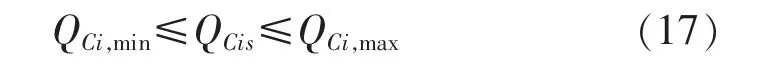
電容器組數約束：

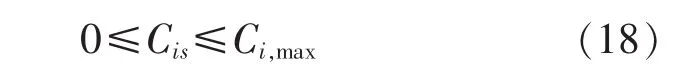
變壓器分接頭檔位約束：

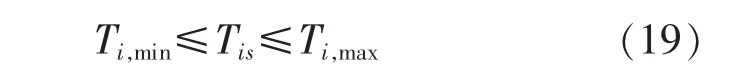
支路傳輸功率約束：

2 基于改進人工蜂群算法的模型求解

2.1 傳統人工蜂群算法

Karaboga在2005年，提出了ABC算法及相關改進算法。將ABC算法應用于實際的工程優化問題。通過與其它智能群優化算法，例如粒子群算法PSO（particle swarm optimization）、遺傳算法 GA（genetic algorithm），進行性能比較，指出ABC算法更適合處理工程中的高維優化問題。

ABC算法描述如下，問題中的各種可能解由算法中的蜜源表示，在尋優的過程中，解的優劣性用適應度函數值的大小表示。引入三種蜂：采蜜蜂，觀察蜂，偵查蜂。采蜜蜂與所求問題的具體解聯系在一起，在求取最優解的過程中通過與其他蜜蜂交換信息來接近最優解，觀察蜂則通過分享采蜜蜂的信息對所求解做出選擇，偵查蜂隨機搜索新位置[7]。

在尋優的過程中，解的質量和選擇概率采用式（21）計算，由觀察蜂做選擇：

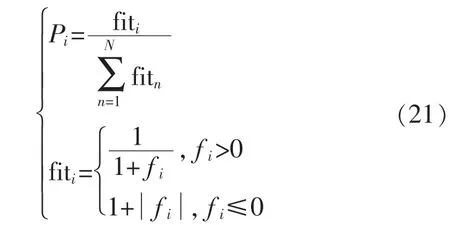
式中：fiti為第i個解所對應的適應度函數值；N為解的數量，等于采蜜蜂的數目。

ABC模型通過式（22）從已求得解對應的個體位置中隨機產生一個新解，即：

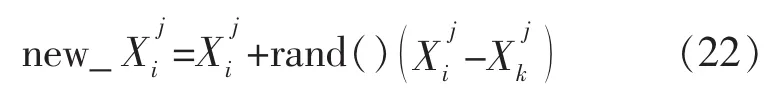
式中：i，k∈｛1，2，…，N｝與 j∈｛1，2，…，D｝是隨機選取的，但k不等于i；D是優化問題參量個數；rand（）取值范圍為［-1，1］，控制蜜源位置 Xij周圍的產量。每個新解new_Xij產生后，該解與Xij進行比較。如果產生的新解所對應的適應度函數值，比舊解所對應的適應度函數值大，則用產生的新解替代原來解；否則，保持原來解不變。

傳統ABC算法作為一種新的工程優化算法，相比于其他優化算法，雖然在很大程度上增加了找到問題最優解的概率，但是在尋優過程中，算法依然存在各種缺點，例如容易過早收斂、個體易陷入局部最優等。為了避免出現上述問題，本文采用改進的高斯變異和混沌擾動的人工蜂群算法，在加強局部搜索能力，避免過早收斂的同時，對導致算法停滯的個體，采用混沌序列對其進行擾動，以跳出局部最優。

2.2 改進的ABC算法

2.2.1 高斯變異

高斯變異描述如下，用符合均值為μ，方差為σ2的正態分布的隨機數來替代原本參數值[8]。變異公式由式（23）表示：

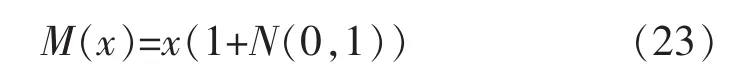
式中：x為原有解；N（0，1）為符合正態分布，期望為0，標準差為1的隨機數；M（x）為經過高斯變異之后的數。

對于工程優化過程中的局部極小值問題，采用高斯變異，可以提高算法的局部搜索能力，能夠在快速、準確找到全局極小點的同時增強算法的魯棒性。

2.2.2 混沌搜索

混沌是一種具有隨機性的運動狀態，由確定的方程通過添加擾動變量得到。傳統ABC算法在求取最優解過程中，如果某個解經過多次迭代之后，其所對應的適應度函數值仍然偏小，則表明對應個體陷入局部最優，而混沌擾動則可以利用混沌變量自身的遍歷性與隨機性，以該解為基礎隨機產生混沌序列，用此混沌序列對部分導致搜索停滯也即陷入局部最優的個體采取一定擾動，以促使算法跳出限制繼續搜索[9]。

考慮Tent映射的值較為平緩，所以選擇Tent映射來產生混沌序列。Tent映射公式為

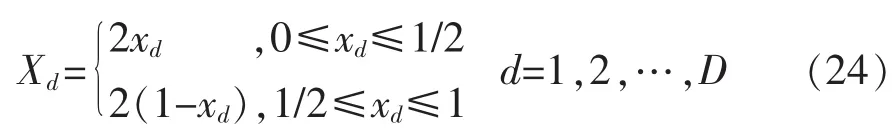
式中：Xd為混沌序列X的第d維向量；xd為一個服從均勻分布的隨機數，xd∈［0，1］。

混沌擾動的步驟描述如下[10]：

（1）應用Tent映射產生的混沌變量；

（2）按照式（25）將混沌變量映射回優化問題的解空間：

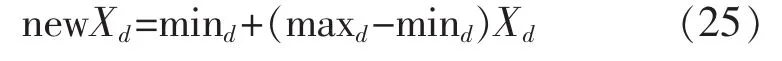
式中：maxd和mind分別為d維向量newXd的最大、最小值；

（3）按照式（18）對個體進行混沌擾動：

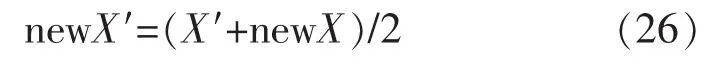
式中：X′為陷入局部最優的個體；newX為隨機產生的混沌擾動量；newX′為擾動后的個體。

2.3 算法應用

（1）初始化，設置配電網參數、蜂群大小等；

（2）隨機產生初始解，計算個體適應度值，記錄當前最優解；

（3）按式（22）尋找新解，對比選擇最優解，其對應的個體位置；

（4）如果尋找新蜜源的次數達到最大值Limit時，還沒有找到更優的解，則隨機產生一個解替代之前解；

（5）計算蜂群中個體的適應度值與平均適應度值，個體適應度大于平均適應度，按式（23）計算，否則按式（26）進行計算，如果變異/擾動后性能更優，則代替之前個體，否則保持原個體不變；

（6）迭代達到最大次數后輸出最后結果，否則返回步驟（3）繼續執行。

無功優化算法求解流程如圖1所示。

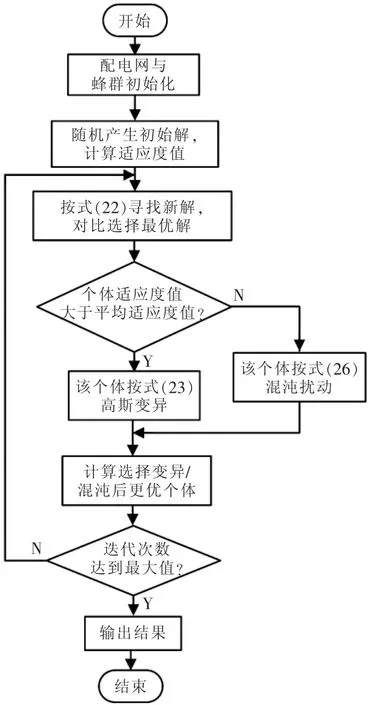
圖1 無功優化算法求解流程Fig.1 Reactive power optimization algorithm solution flow chart

3 算例分析

本文采用如圖2所示的IEEE-33節點系統進行分析，該系統的電壓等級為12.6 kV，總負荷為3715 kW和2300 kvar，原始網絡數據參數參見文獻[11]。為驗證本文所提方法，對該系統做如下修改。在節點6、節點13、節點30各安裝20組電容器，每組容量50 kvar；在節點10、節點20接風電機組，所有機組參數設置相同；在節點16、節點24接光伏發電系統，所有DG額定容量均為800 kW，功率因數為0.95；有載調壓變壓器額定容量為50 MVA，檔位調節范圍為0.9～1.1，分為9檔；節點電壓上下限允許范圍為0.9～1.1。風電機組和光伏發電機組參數如表1和2所示。

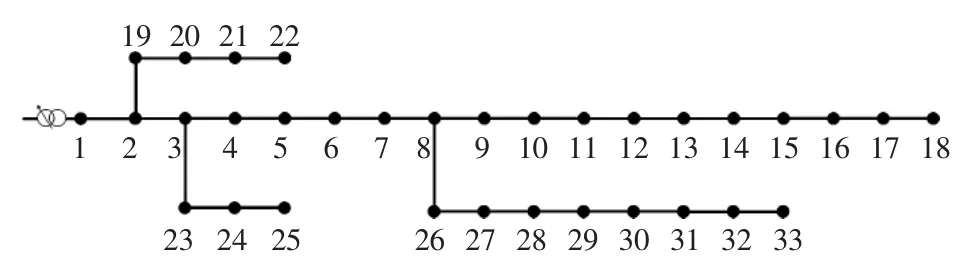
圖2 IEEE 33節點系統結構Fig.2 IEEE 33-node system structure

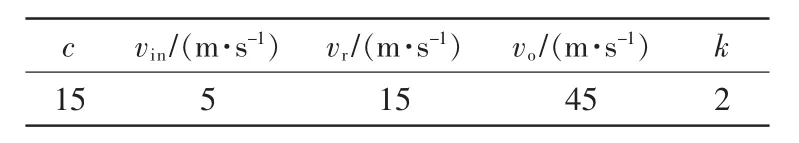
表1 風電機組參數Tab.1 Wind turbine parameters

表2 光伏發電參數Tab.2 Photovoltaic power generation parameters

為了實現DG接入配電網后的安全穩定運行，需要準確掌握DG出力的變化情況，精確預測發生的各場景。圖3為風電機組和光伏發電，典型日出力曲線，與采用Wasserstein距離法得到的隨機場景曲線對比圖。從圖中可以看出，本文所提的最優場景法能夠全面反映風機和光伏出力的隨機性。圖中P為風電、光伏機組的實際功率，Pn為風電、光伏機組的額定功率。

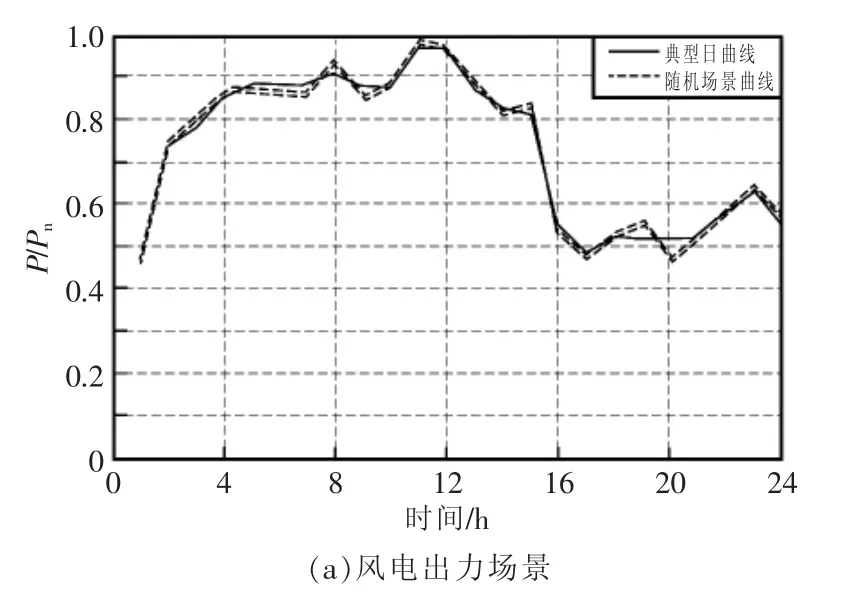
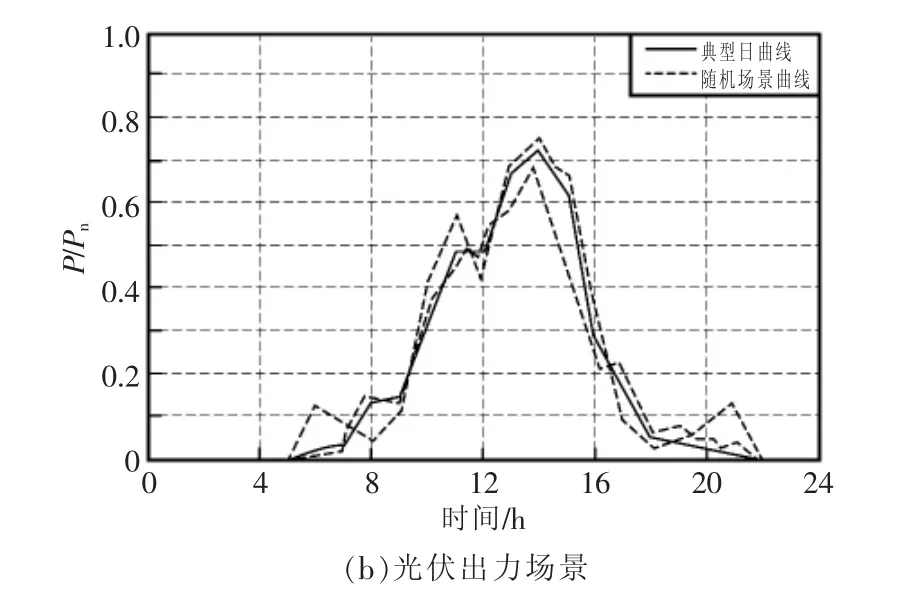
圖3 風電和光伏出力場景Fig.3 Scenario wind power and PV power output

圖4為GA、傳統ABC和改進ABC算法尋優的對比收斂曲線。從圖中可以看出，改進ABC算法，相比其他兩種算法收斂速度更快，精度更高，優化效果更好。因此，應用改進ABC算法求取全局最優解，能夠有效減小含DG配電網的有功網損與電壓偏差。

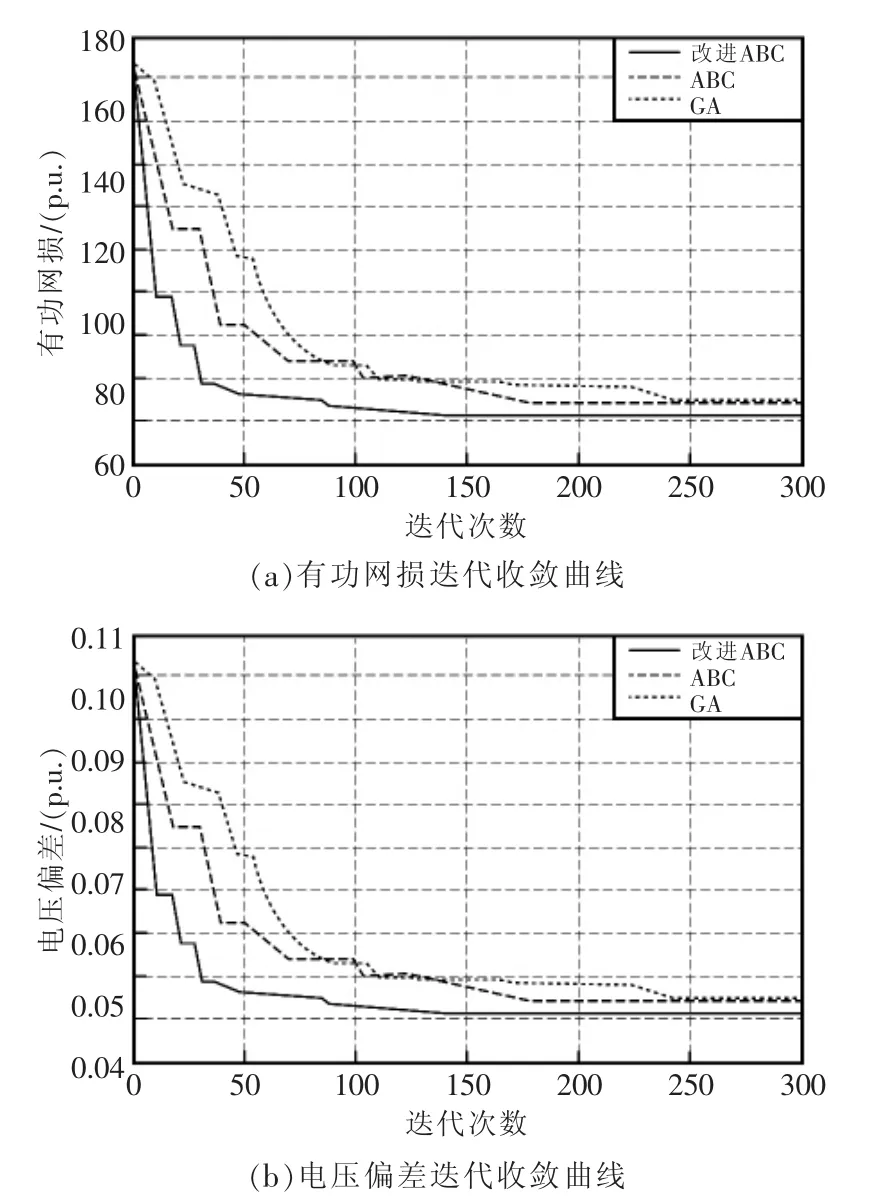
圖4 優化算法收斂特性曲線Fig.4 Optimization algorithm convergence characteristic curve

圖5為IEEE-33節點測試系統在改進ABC算法優化前后，各節點電壓分布情況對比圖。從圖中可以看出，優化前，配電網線路末端節點的電壓有效值較低，電能質量較差，優化后，各節點電壓得到有效補償，尤其是配電網末端電壓，提高了電能質量。

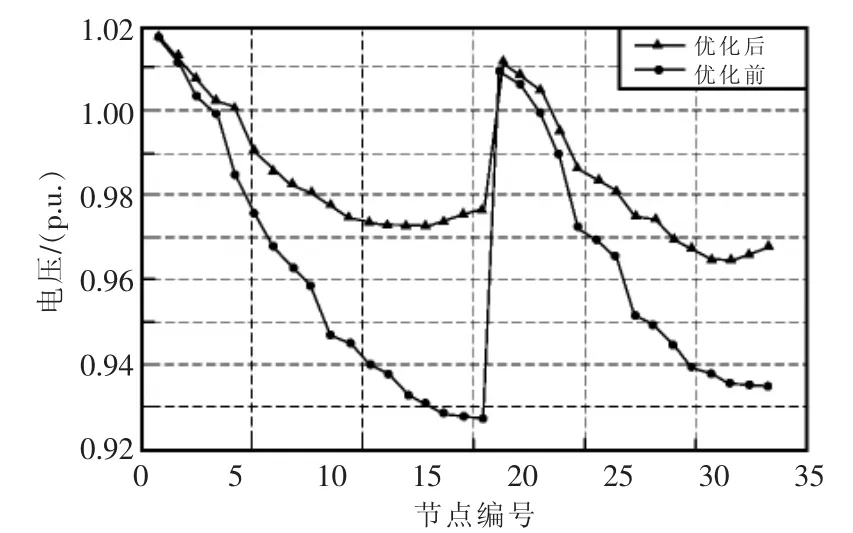
圖5 優化前后節點電壓對比Fig.5 Comparison of node voltage before and after optimization

4 結語

本文針對含DG的配電網無功優化問題，首先基于系統中DG與負荷的隨機性問題，采用最優場景法模擬風機、光伏出力與負荷的波動性。然后建立了以網損、電壓偏差最小為目標函數的數學模型，提出基于高斯變異和混沌擾動的人工蜂群算法，對模型進行優化求解。最后，在改進的IEEE-33節點配電網系統中進行分析。結果表明，該方法能夠有效改善電能質量，提高電壓水平，而且相比于GA、ABC算法，改進ABC算法收斂速度更快，搜索精度更高，性能更優。