基于時間序列的股票價格走勢分析
摘要:隨著當代經濟的不斷發展,金融市場已經成為經濟發展的重要部分,而股票市場作為金融市場的重要組成部分,便與國民經濟密切相關。對于投資者而言,如何及時了解價格波動從而準確分析股票市場行情,是決策過程中的一個關鍵問題;對于股票市場的管理者來說,如何把握股市動態,從而營造穩定健康的交易環境,也是一項非常艱巨的任務。因此,更好地了解股市的波動特征,以及從中探索某些規律,對我們學習金融理論和進行金融實踐都具有重要的意義。本文以2009-2018年的滬深300指數為例,對ARIMA模型、ARCH模型和AR-GARCH模型進行擬合,比較其在股票價格走勢上的優劣,再用通過檢驗的擬合模型對股價進行一個短期的預測。最后發現AR-GARCH模型對原序列有較好的擬合效果,并且獲得了較為精確的預測結果。
關鍵詞:時間序;ARIMA模型;ARCH模型;AR-GARCH模型
1.數據預處理
1.1? 平穩性檢驗
本文選取了2009年1月至2018年12月的滬深300指數每個工作日的收盤價作為研究對象,繪制其時序圖并作出初步分析。
由原序列時序圖可以看出,該序列有不太明顯的周期性,直接觀察無法確定其是否平穩,此時我們可以借助自相關圖進一步判斷序列是否平穩。
根據原序列的ACF圖可以看出,隨著延遲期數k的增加,ACF一直在零軸上方為正,而且衰減到零的速度非常慢,因此可以判斷原序列為非平穩序列。
1.2? 純隨機性檢驗
此時,再檢驗序列的純隨機性。結果顯示,在各階延遲下LB檢驗統計量的P值都遠遠小于0.05,因此可以確定原序列屬于非白噪聲序列,有繼續研究下去及對未來預測的意義。
2.股票價格建模
2.1? ARIMA模型
差分運算有著非常強大的確定性信息提取功能。通常來說,具有隨機性趨勢的非平穩時間序列會在適當的差分之后顯示出平穩序列的性質,此時我們稱這個非平穩序列為差分平穩序列。對于這種差分平穩序列我們就需要利用ARIMA模型來進行擬合。
一階差分后的時序圖顯示,序列一直圍繞零軸波動,沒有明顯的規律,此時用單位根檢驗得p值<0.05,所以拒絕原假設,可以認為序列平穩。然后,再對一階差分后的序列進行白噪聲檢驗,得到在各階延遲下LB檢驗統計量的P值都<0.05,因此得出一階差分后的序列是平穩非白噪聲序列,可以使用ARIMA模型對其進行擬合。
可以認為自相關系數和偏自相關系數均顯現出了拖尾性,無法準確定階。此時利用R軟件提供的auto.arima函數自動識別模型階數,最終確定對原序列擬合ARIMA(3,1,2)模型。
這時對模型進行顯著性檢驗來檢驗模型的有效性。由于各階延遲下LB統計量的P值都大于0.05,因此可以認為這個擬合模型的殘差序列屬于白噪聲序列,即該擬合模型是顯著有效的。
根據輸出的擬合結果,得到擬合模型為:
2.2? ARCH模型
當使用ARIMA模型擬合非平穩序列時,通常直接默認[εt]為零均值白噪聲序列。但在此之前,直接忽視了對方差齊性的任何檢驗,就直接默認了殘差序列肯定滿足這樣一個條件。在處理金融時間數據時,忽視異方差的存在會嚴重低估殘差的方差,使得參數的顯著性檢驗失去意義,進而使模型的擬合精度受到影響。
在實際處理金融數據時,廣泛采用的還是自回歸條件異方差模型,簡稱ARCH模型。
具有
結構的模型稱為q階自回歸條件異方差模型,簡記為ARCH(q)。
考察原時間序列的方差齊性,經過平方處理后的殘差序列明顯地呈現出異方差的特征,這時需要對它做進一步的處理。由于異方差函數的具體形式未知,因此擬合條件異方差模型。
接下來對殘差序列進行ARCH檢驗。通常使用Portmanteau Q檢驗和LM檢驗這兩種檢驗統計方法。檢驗后發現,在各階延遲下,Portmanteau Q檢驗統計量和LM檢驗統計量的P值均<0.05,所以拒絕原假設,認為該序列方差非齊且具有自相關關系,可以使用ARCH模型來提取殘差平方序列中蘊含的相關信息。
得到擬合模型是ARCH(3)模型:
ARCH模型擬合的95%置信區間的范圍,因為考慮了一階差分后序列的波動特征,所以ARCH模型更好地擬合了一階差分后序列的集群效應波動特征。
2.3 AR-GARCH模型
由于殘差序列[et]在先前的檢驗中已被發現具有自相關性,所以需要先對它進行自回歸模型的擬合。
在條件異方差檢驗下,各階延遲下Portmanteau Q檢驗統計量均小于0.05顯著性水平,說明ARIMA(3,1,2)存在異方差,于是對它擬合GARCH(1,1)模型,并根據該模型的擬合結果繪制波動的95%置信區間圖。
綜合水平模型和波動模型,最終得到完整的AR-GARCH擬合模型為:
圖2-2給出了AR-GARCH模型擬合的殘差序列波動置信區間,
進行比較后,發現AR-GARCH模型擬合結果繪制的95%置信區間比ARCH模型擬合的95%置信區間更加貼合原序列的真實波動情況,說明AR-GARCH模型的擬合效果更好,對序列波動的預測也將更加準確。
2.4? 模型比較
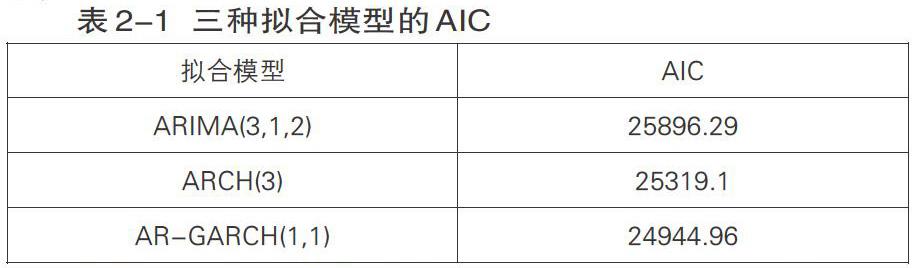
本章對滬深300股票價格進行了ARIMA(3,1,2)、ARCH(3)和AR-GARCH(1,1)三種模型的擬合,三種模型都通過了顯著性檢驗,且都獲得了不錯的擬合效果。為了得到一個相對最優的擬合模型,需要運用最小信息量準則(AIC)來對這三個模型進行比較。我們運用如下公式來計算擬合模型的AIC的值:
AIC=-2ln(模型的極大似然函數值)+2(模型中未知參數個數)
根據AIC最小原則,比較得出AR-GARCH(1,1)是相對最優模型,ARCH(3)次之,ARIMA(3,1,2)再次之。
3.模型預測
3.1? AR-GARCH模型預測
選取相對最優模型,利用“rugarch”程序包用擬合好的AR-GARCH模型做預測,并將殘差序列的預測值轉化為原序列的預測值
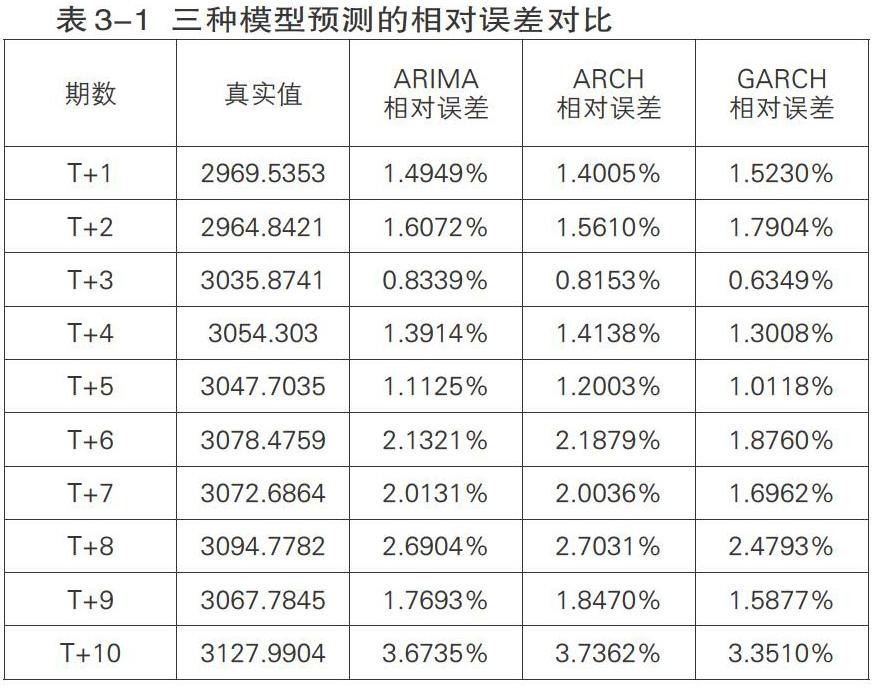
由于此時已經得到了滬深300指數未來10天收盤價的真實值,于是可以通過比較真實值與預測值的誤差來判斷模型預測的優劣。接下來將三種模型獲得的預測值與真實值進行比較:
其中,ARIMA(3,1,2)模型與ARCH(3)模型預測值的相對誤差非常接近,可以認為這兩種模型的預測效果差不多。而GARCH(1,1)模型的相對誤差明顯小于前兩個模型,可以認為GARCH(1,1)模型的預測精度是最高的,即預測結果會更接近真實值。這個結果也與上一章比較模型優劣的結果一致。
3.2 橫向預測
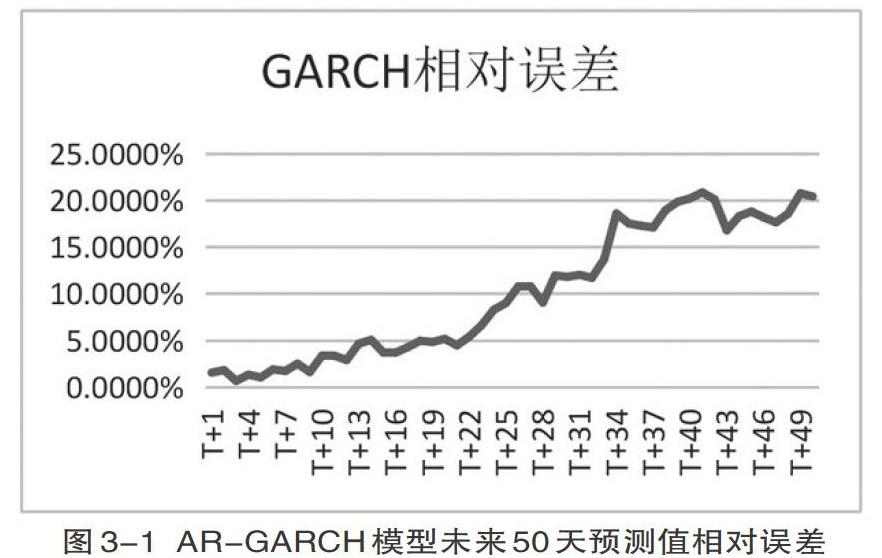
為了檢驗模型的長期預測效果,這里選用上述模型中預測效果最好的AR-GARCH(1,1)模型來對未來50天(約為2019年1-2月份)的收盤價進行預測。
由圖3-1可以很明顯地看出,隨著期數的增加,AR-GARCH(1,1)模型的預測值與實際值的相對誤差逐漸增大,到第50期時,相對誤差已經超過了20%,也就是說該模型的預測精度越來越低,已經失去了準確預測收盤價的能力。
4.結論
本文主要討論了求和自回歸移動平均模型和條件異方差模型在股票價格時間序列分析中的應用。通過對滬深300股價進行三種模型的擬合,都成功建立了顯著性模型,再一次證明了股票價格的可預測性:
(1)在本文研究的案例中,殘差序列的異方差函數是具有長期自相關性的,因此在使用ARCH模型進行擬合時會產生高階移動平均,而用GARCH模型擬合時就可以克服這一問題,提高擬合精度。所以對于股票價格時間序列這類異方差函數長期自相關的序列,選擇使用GARCH模型擬合可以獲得相對最優的擬合效果,從而得到更準確的預測。
(2)短期預測的結果與實際值相差并不大,預測的相對誤差基本可以控制在2%以內,說明擬合的效果非常好,可以利用該模型對近期股市進行短期預測,幫助投資者做出更好的投資決斷。但是在使用該模型進行長期預測時,結果不盡如人意,預測精度明顯下降,失去準確預測的能力。
(3)時間序列作為金融市場分析的有效工具,有著巨大的實用價值和發展前景。通過時間序列來探尋股票價格波動的規律,對投資者進行投資決策、規避風險、獲得最大收益有重要的參考意義。然而對股票市場規律的研究是十分復雜的,本文僅通過歷史數據對滬深300的走勢進行了一些分析和預測,并未考慮股票的投資收益率、風險溢價等指標,如何處理原始數據并選擇最優模型還需要進一步的研究來完善。
作者簡介:
黃旻浩(1996-? ),男,漢族,江蘇省無錫市人,香港中文大學理學碩士研究生在讀,統計機器學習。

