異形鋼結構建筑鑄鋼節點空間加載試驗與有限元分析

□文/高樹才 吳伸杰 馬 旭 榮 彬

鑄鋼節點具有受力明確、傳力直接、承載力大的特點，通常節點體型大、受力復雜，多用于結構體系的關鍵節點，其可靠性直接影響結構的安全，而目前的理論分析和設計方法尚不成熟，僅依靠數值模擬的結果進行設計顯得不夠安全，因此國內外的重點工程都對不同形式的鑄鋼節點的受力性能開展研究。丁陽等[1]為考察天津奧林匹克中心體育場大跨度鋼管桁架結構鑄鋼節點的受力性能，評價其安全性，對鑄鋼節點進行了足尺試驗驗和有限元分析，結合試驗結果和有限元計算結果，分析了節點的應力分布規律，表明天津奧林匹克中心體育場鑄鋼節點具有較高的承載性能和足夠的安全性。徐世杰等[2]通過試驗研究了重慶江北機場T3A航站典型鑄鋼節點的荷載-位移曲線，應力和節點破壞時的變形特征，使用有限元軟件進行驗證，對此類異形鑄鋼節點的使用和施工過程提出了優化建議。杜新喜等[3]對新疆國際會展中心屋面張弦桁架支座鑄鋼節點進行了1/2縮尺加載試驗，試驗結果表明在最不利設計工況組合下，節點滿足設計的承載力要求；對節點試件進行了彈塑性有限元分析，有限元分析和試驗結果吻合良好，在有限元數值模型可靠的基礎上，對鑄鋼節點的承載性能指標和安全儲備進行了綜合評估。上述工程實例表明了鑄鋼節點具有良好的適用性，由于國內還沒有一套成熟的鑄鋼節點設計方法，目前工程中的鑄鋼節點多采用有限元理論分析與試驗測試結果相結合的方式來保證節點的承載安全性。

1 工程概況

中部國際設計中心建筑方案是著名國際建筑設計大師扎哈·哈迪德的遺作，裙房底盤平面形狀呈不規則五角星形，形似花瓣。上部三角布置3棟塔樓，整體協調，渾然一體，見圖1。

圖1 中部國際設計中心

塔樓的形態以“花”為設計意向，外輪廓底部呈現弧線形的花萼形態，塔身賦以白色線條表示花的經絡，輕盈曼妙。塔樓平面呈紡錘形的六邊形。裙房外墻為直線曲線結合的橫向玻璃帶窗和鋁板幕墻組合，形成流暢的建筑外立面。塔樓的塔基從下到上逐漸擴大到裙房屋面之上后慢慢內收，塔樓以玻璃幕墻和豎向裝飾線條形成花瓣的肌理。

結構的難點在于塔樓3層以下外排鋼管柱向核心筒逐步回收至內排柱，在一層交匯，部分節點由三斜管交匯，交匯位置受力復雜。若采用相貫焊接將導致焊接應力過大，很難判斷節點是否達到承載要求，故采用了鑄鋼節點。

2 節點概況

工程使用的鑄鋼節點的節點形式見圖2。

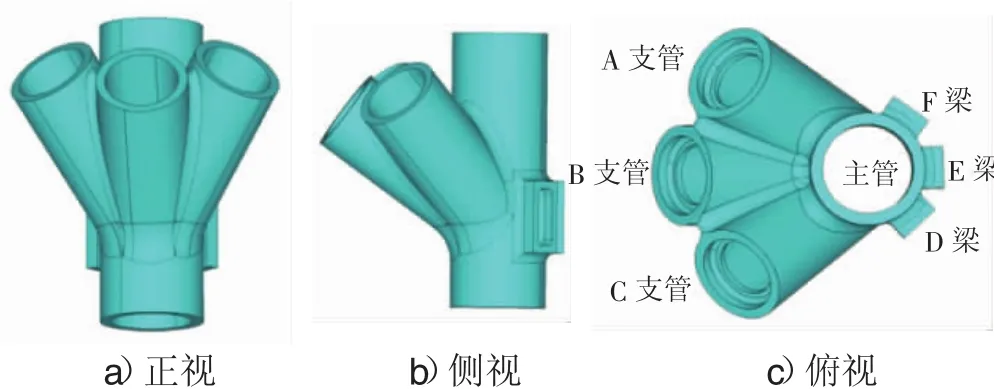
圖2 節點模型

主管豎直連接下層柱子，主管的前部與三根斜管相貫，后部支撐3根水平梁。節點為1/2縮尺模型，主管外徑為450 mm、壁厚45 mm，各支管外徑400 mm、壁厚40mm，主管后三個水平梁截面尺寸340 mm×165 mm×35 mm，各管交匯區域上部倒角尺寸為30 mm，下部的倒角尺寸為200mm。

3 鑄鋼節點試驗

3.1 加載工況

鑄鋼節點試驗在天津大學結構試驗室進行，加載采用設計組合工況，對于各管而言，設計荷載的軸力起控制作用，因此選擇主管，支管B、C的最大軸力工況進行空間加載試驗。見表1。

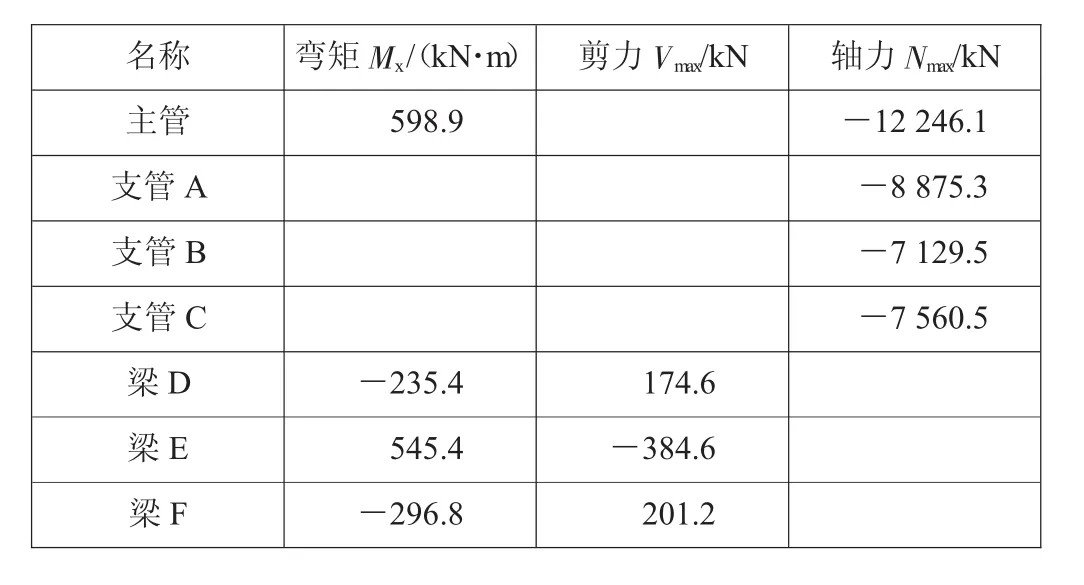
表1 試驗荷載

表1中彎矩以梁的下部受拉為正，反之為負；剪力以使研究桿段轉向為順時針時為正，反之為負；軸力以受拉為正，受壓為負。試驗中加載的荷載為縮尺模型按照應力等效原則對應的換算值。

3.2 材性試驗

鑄鋼材料選用G20Mn5QT，采用和節點同爐澆筑的方法進行試棒加工，見圖3。

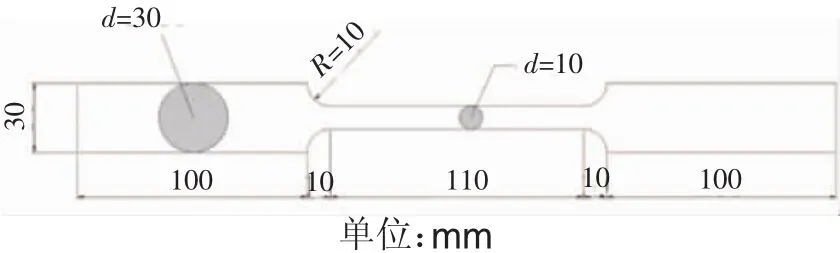
圖3 材性試驗試棒尺寸

3.3 試驗裝置

空間試驗載裝置見圖4。

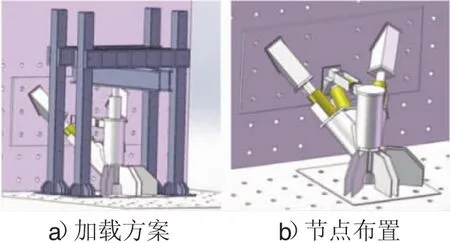
圖4 試驗裝置

主管的豎向軸力由320 t單向千斤頂施加，加載分級通過油壓表控制；水平剪力通過50 t單向千斤頂來施加，加載分級通過力傳感器控制；各支管的軸力由3個200 t單向的千斤頂施加，通過設計的支座傳力至反力墻，加載分級通過油壓表控制。

主管豎向力通過上端橫梁傳遞給兩側的加載反力架。加載支管的斜向千斤頂連接加載支座并支承于反力墻上。主管底部焊接底板并在底板上設置支座，以焊接連接水平梁，整個節點采用錨栓固結在地面。

3.4 加載制度

試驗加載分為預加載和正式加載，預加載階段施加設計荷載的30%，分三級加載，然后卸載，為正式加載做準備。預加載結束后，進行正式加載。為保證各管加載的同步性，荷載分10級加載，加載到每級荷載后持荷，采集應變數據后進行下一級加載。

3.5 測點布置

鑄鋼節點應變測點布置見圖5。在有限元分析的基礎上，將測點布置在節點應力集中的節點倒角部位。1號節點試件共布置應變花22個，應變片22個；2號節點試件增加柱底水平梁一側5個應變花。

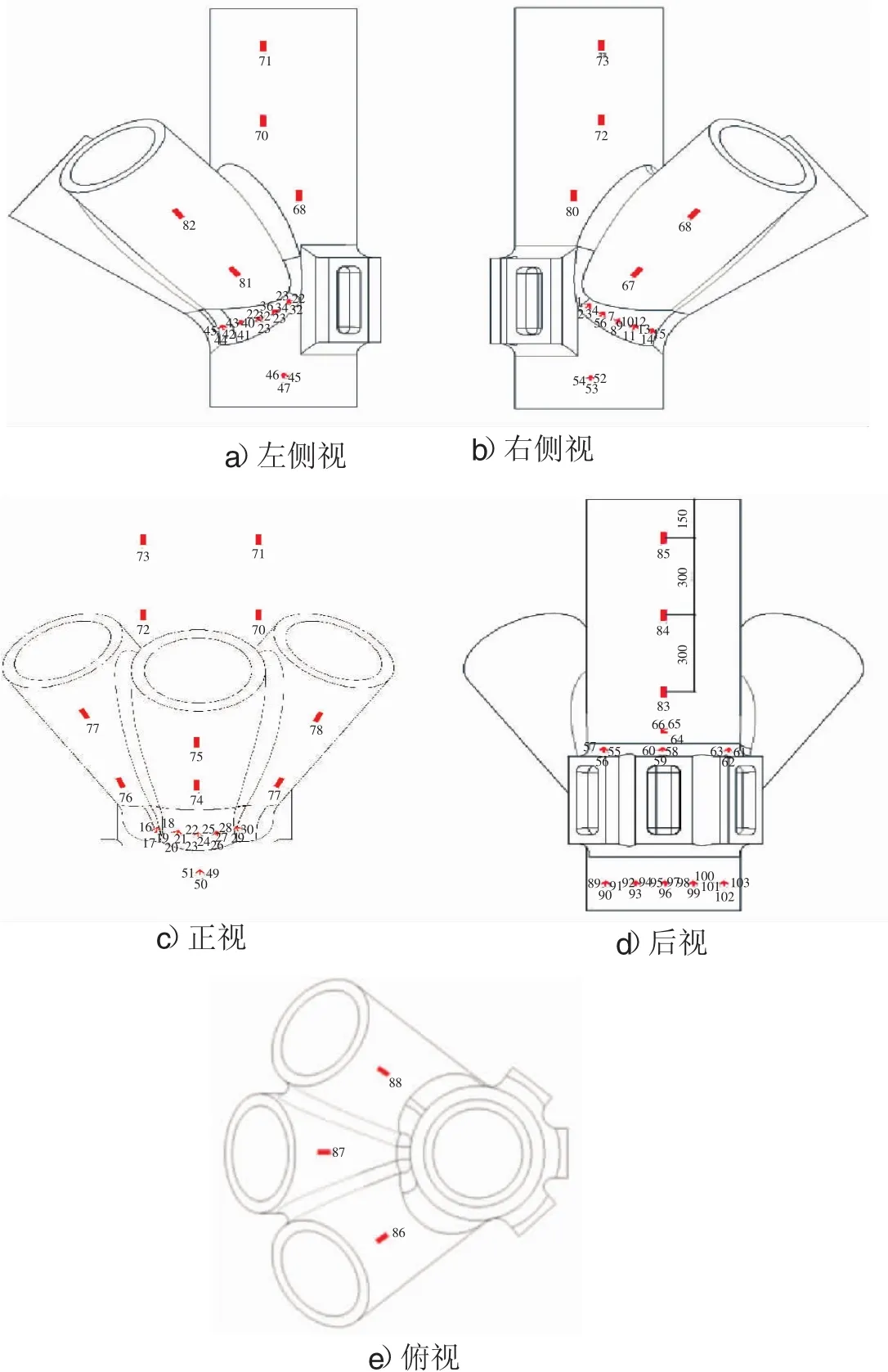
圖5 試驗測點布置

3.6 試驗結果分析

為方便表述，使用應變花中編號最小的應變片，來指代這個應變花（例如應變片花1號為應變片1,2,3組成的應變花）。試驗結果統計中，將應變花和應變片的測量結果換算為測量位置的等效應力。見圖6和圖7。

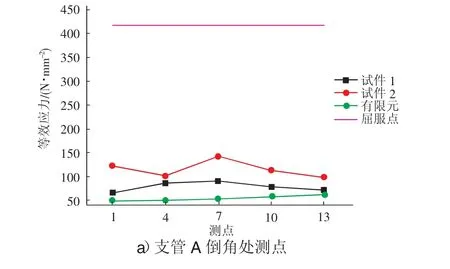
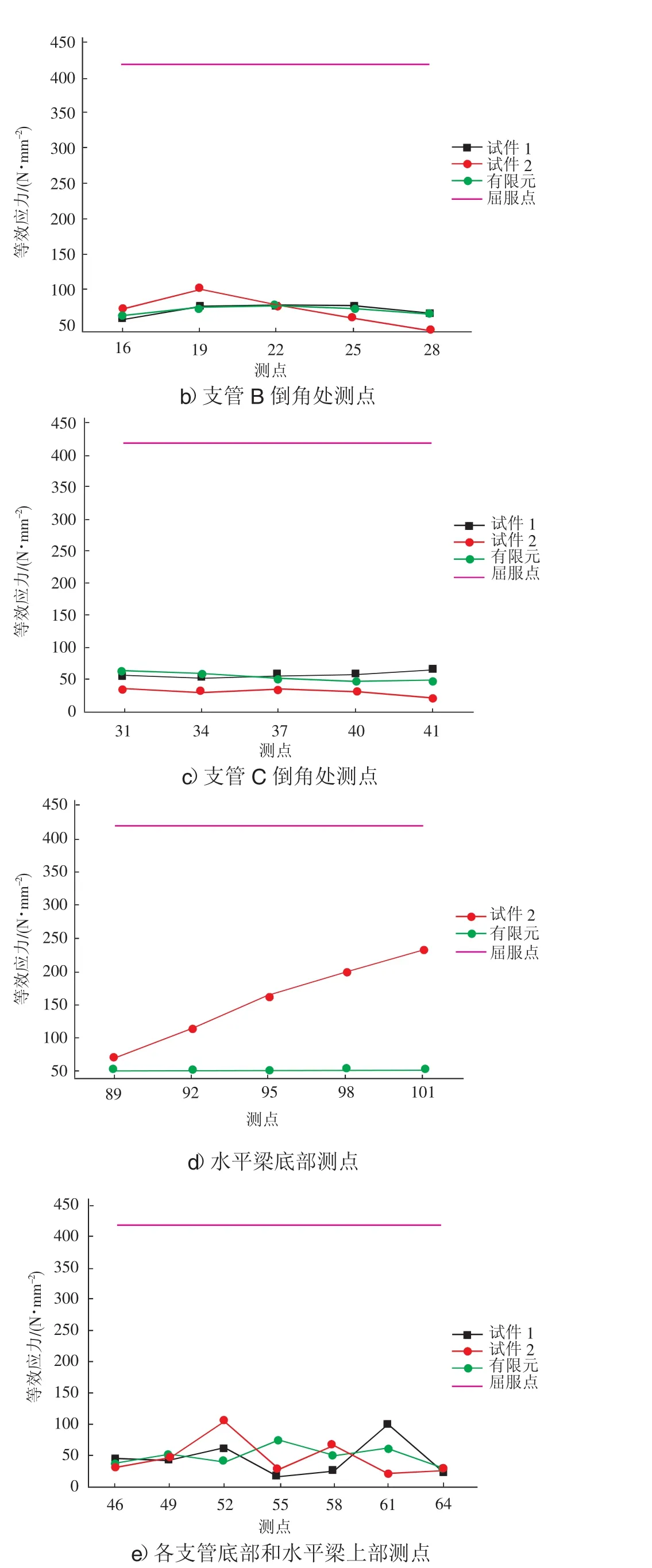
圖6 應變花等效應力

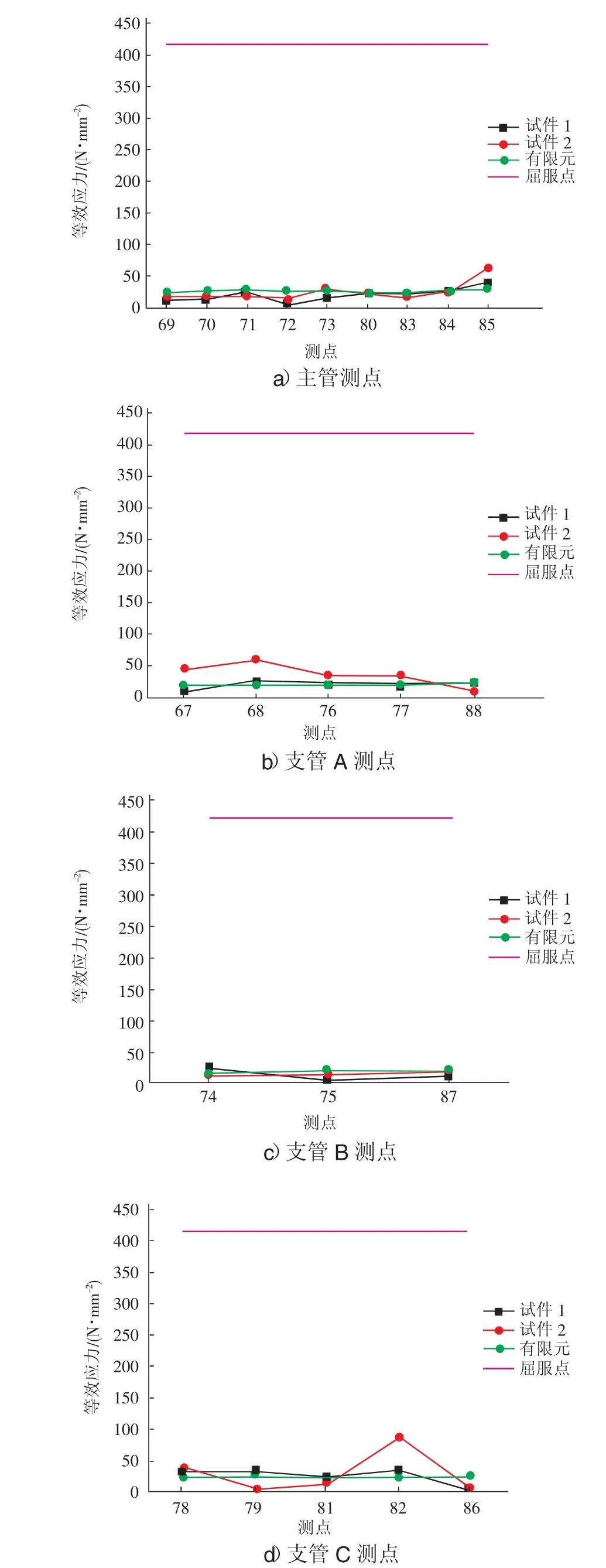
圖7 應變片等效應力

1號節點的最大等效應力為98.74 N/mm2，出現在61號應變花，位于水平梁F上側。A支管倒角處的應變花為1～13號，最大等效應力為89.93 N/mm2。B支管倒角處的應變花為16～28號，最大等效應力為73.44 N/mm2，C支管倒角處的應變花為31～43號，最大等效應力為62.01 N/mm2。應變花46、49、52號為測量主管柱底部的應力水平，較支管倒角部分，此處的等效應力相對較小。應變花55、58、61號測量的是水平梁上側等效應力大小，最大等效應力為98.74 N/mm2。水平梁上部的應變花64號的應力較小。

2號節點的最大等效應力為233.47 N/mm2，出現在101號應變花，位于水平梁F的下部靠近柱底。A支管倒角處的應變花為1～13號，最大等效應力為142.60 N/mm2。B支管倒角處的應變花為16～28號，最大等效應力為98.18 N/mm2，C支管倒角處的應變花為31～43號，最大的應力為 32.06 N/mm2。應變花 46、49、52號為測量主管柱底部的應力水平，較支管倒角部分，此處的等效應力相對較小。應變花55、58、61號測量的是水平梁上側的等效應力，最大值為65.06 N/mm2。水平梁上部的應變花64號的應力較小。應變花89、92、95、98、101號測量的是柱底水平梁一側的等效應力，最大值為233.47 N/mm2。

應變片主要測量的為主管，支管管壁的應力大小，除2號試件支管A管壁82、85號測點等效應力較大，其他測點應力較小。在試驗荷載下，節點在各支管底部倒角處和節點底部的應力水平相對較高，起到控制作用，管壁的應力相對較小。

4 有限元分析

4.1 有限元模型

有限元分析中，節點模型采用solid187單元模擬，solid187單元是10節點四面體單元，具有塑性、大變形和大應變特點，適用于模型的復雜網格劃分。鑄鋼的材料屈服強度417.63 N/mm2，抗拉強度554.29 N/mm2，彈性模量為2.13×105 N/mm2，泊松比0.3。有限元分析中鑄鋼材料采用理想三折線隨動強化應力應變模型，見圖8。

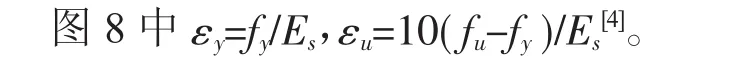
有限元分析中，采用Von Mises屈服準則，顯示對比結果的Von Mises應力。為保證分析結果的準確性，網格尺寸選擇為節點管壁厚的1/2[5]，節點的網格劃分見圖9。為準確模擬試驗中節點的受力狀態，約束了節點底部和水平梁端的全部位移和轉動。

圖8 有限元分析中鑄鋼材料的本構模型

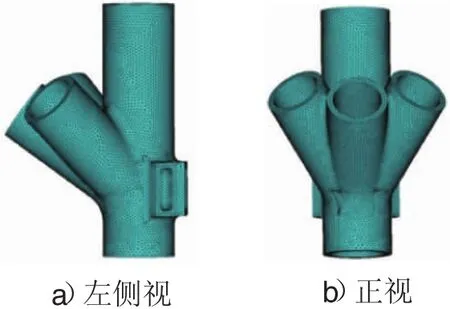
圖9 鑄鋼節點的網格劃分

4.2 有限元結果和試驗結果對比

有限元分析的結果見圖10，試驗荷載下有限元分析結果和試驗結果對應測點的應力大小對比見圖6和圖7，有限元分析結果與試驗結果整體較接近，證明有限元分析的可行性。

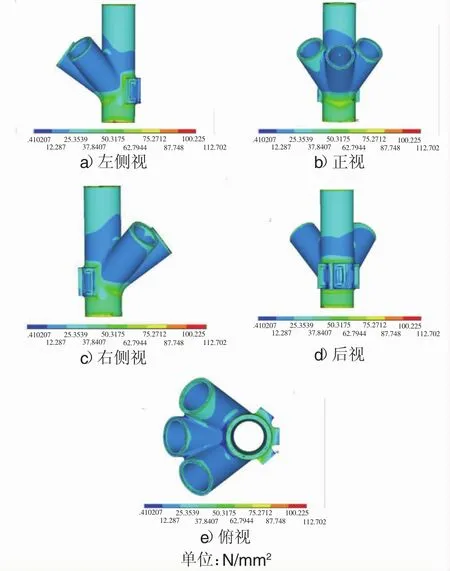
圖10 有限元分析結果

對于有限元的結果，最大的等效應力出現在節點底部約束處，其次應力較大的部位仍是各支管下部的倒角部分，其中B支管下部倒角部位的等效應力更大。

5 結論

鑄鋼節點試驗中，全部試驗節點的最大應力均不超過屈服強度。對于1號節點試件，應力量測結果與有限元結果吻合較好，驗證了有限元分析的可行性。對于2號節點試件，A支管和C支管應力出現明顯的不對稱性，節點受力不均勻，與節點實際受力情況不符，表明節點制作和安裝誤差對節點受力有較大影響，施工中應注意節點制作和安裝精度。

試驗結果表明，在最大設計荷載工況下，節點最大的等效應力為233.47 N/mm2，有限元結果表明，最大的等效應力為51.24 N/mm2，均小于材料屈服強度417.63 N/mm2。試驗和有限元分析表明,節點的主管、支管底部和水平梁下部倒角處應力水平較高，施工時應注意這些位置處的應力監測。