一種限定混沌狀態變量運動區域的方法*

趙柏山，劉曉曉，張學松

(沈陽工業大學 信息科學與工程學院，沈陽 110870)

自20世紀60年代Lorenz發現了第一個混沌系統以來，混沌理論的研究和應用在物理學、生物學、信息科學等許多領域得到了廣泛關注.Lorenz系統在混沌學的形成和發展中起到了不可替代的作用，因而成為后人研究混沌系統的基點.以Lorenz系統為基礎，研究者們提出了各種新型混沌系統，如基于電流反饋運算放大器的憶阻混沌電路系統[1]、基于混沌系統部分序列參數辨識的混沌保密通信系統[2]、基于分數階的自適應滑模混沌通信系統[3]、磁控二氧化鈦憶阻混沌系統[4]以及含三個憶阻器的六階混沌電路[5]等.基于混沌信號的寬頻譜、類隨機的混沌特性，混沌信號在多種新型混沌通信系統中得到了廣泛應用，如基于比例積分反饋控制器的Lü混沌系統的同步實現[6]、低信噪比下混沌擴頻數據的快速捕獲[7]、獨立同分布密鑰流混沌通信系統的構建[8]以及基于混沌特性的微電網孤島的檢測[9]等.

然而，由于混沌信號的功率譜分布并不理想，現有的研究成果無法利用混沌信號作為通信載波實現信號的無線傳輸，這已經成為目前制約混沌信號在無線通信領域應用的一個重要因素.相關研究[10]發現，系統狀態變量的相空間運動軌跡與混沌信號功率譜分布具有相關性，因此，可以從狀態變量的相空間運動軌跡約束角度來獲取具有不同頻譜特性的混沌信號.

1 模型的構建和動力學分析

1.1 新混沌系統模型的構建

早在2001年，人們根據Lorenz系統和Chen系統，提出了Lü混沌系統，其非線性微分方程式可以表示為

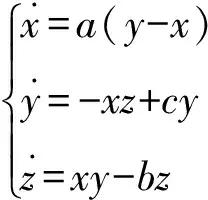
(1)

式中：x、y和z為系統的狀態變量；a、b和c為實常數.

當a=36、b=3且c=20時，Lü混沌系統的狀態變量相空間軌跡如圖1所示.此時狀態變量的功率譜如圖2所示，其中P為功率譜密度，f為頻率.由圖1、2可見，Lü混沌系統的吸引子類似于“蝴蝶雙翼”，其信號功率譜中0 dB對應的頻率約為300 Hz.

在Lü混沌系統的基礎上，通過增加一個非線性約束項并調整相應參數來構建新的混沌系統，其非線性微分方程式可以表示為

(2)

當a=2.65、b=100且c=400時，本文對該新系統進行了理論分析.

1.2 基本動力特性分析

1.2.1 對稱性和不變性

由于新混沌系統在(x，y，z)→(-x，-y，z)變換下具有不變性，因此，得出新系統的相軌跡是關于z軸對稱的，且這種對稱不受系統參數a、b和c的影響.

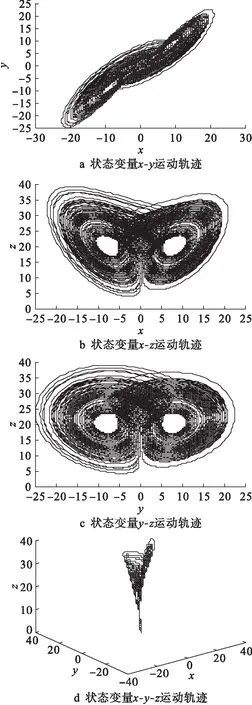
圖1 Lü混沌系統的相空間運動軌跡Fig.1 Phase space motion trajectories of Lü chaotic system

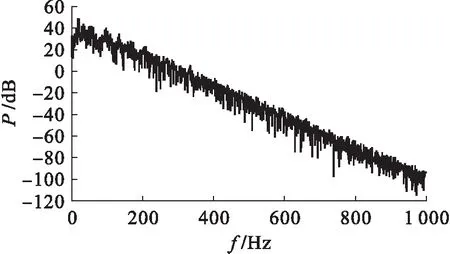
圖2 Lü混沌系統狀態變量的功率譜Fig.2 Power spectrum of state variable of Lü chaotic system

1.2.2 時域圖、Poincaré截面圖與Lyapunov指數

混沌信號具有非周期性、寬頻譜、類噪聲等特點.圖3為新混沌系統的時域波形圖.由圖3可見，新系統中的混沌信號同樣具有非周期性特點.

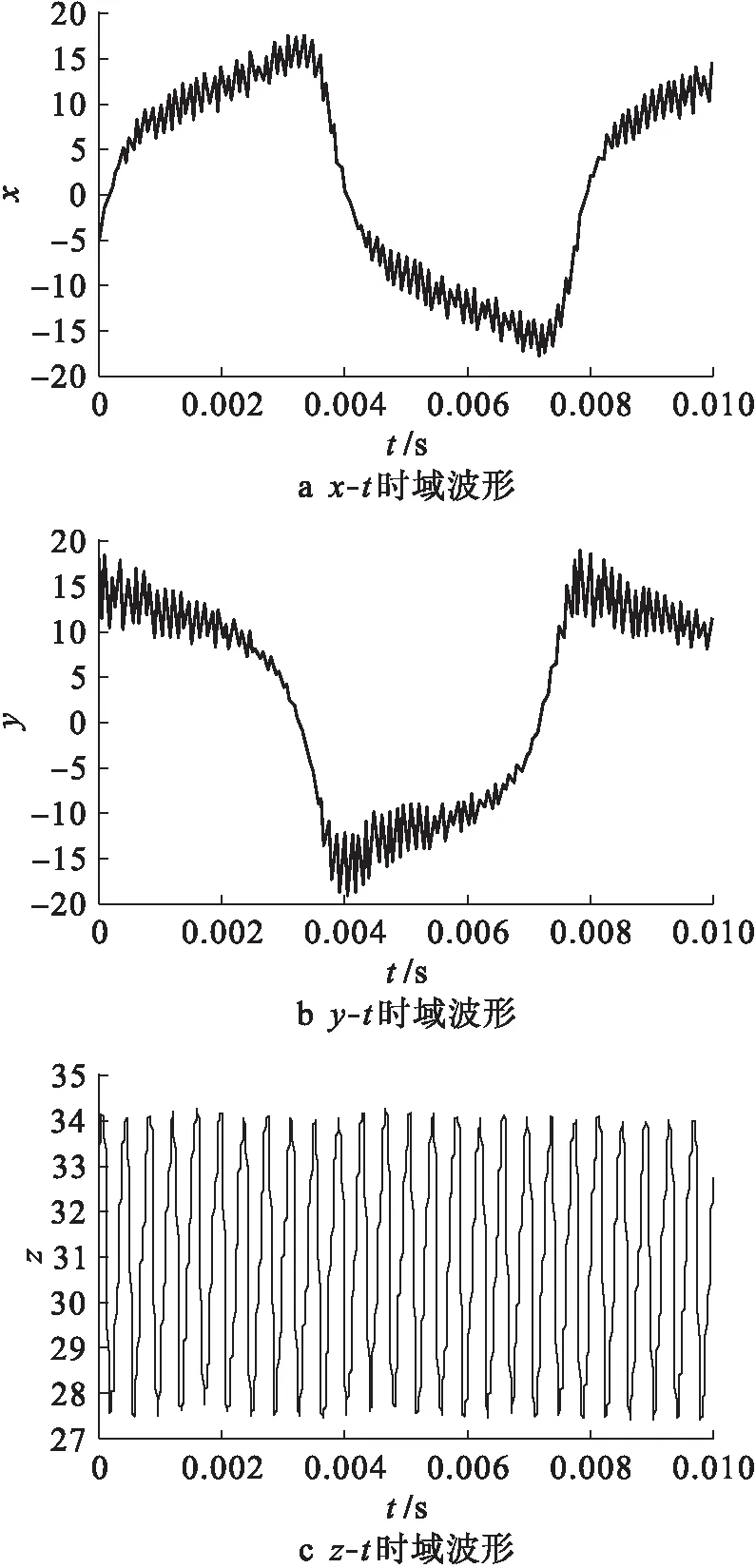
圖3 新系統的時域波形圖Fig.3 Time-domain waveforms of new system

Poincaré截面圖可以描述出混沌運動的往復非周期性，如果Poincaré截面既不是有限點集也不是封閉曲線，則對應的系統運動處于混沌運動狀態.新系統的Poincaré截面圖如圖4所示.

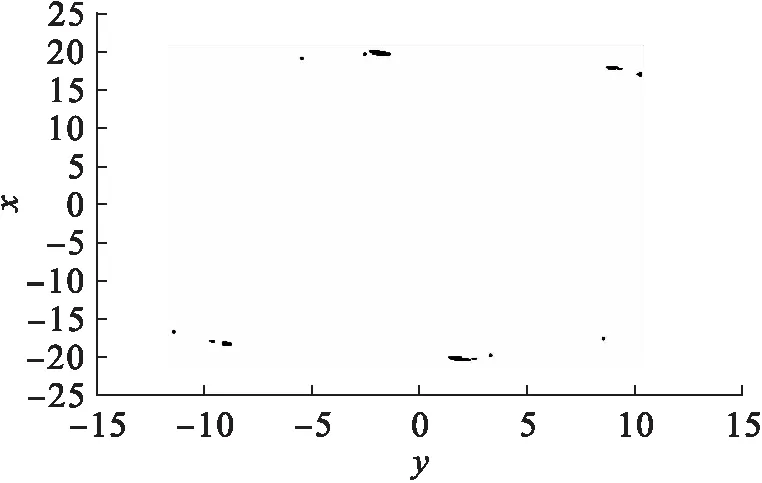
圖4 新系統的Poincaré截面圖Fig.4 Poincaré section diagram of new system

由圖4可見，在Poincaré截面處發現一些成片分布且具有分形結構的密集點，因而可以判斷該新系統為混沌系統.

Lyapunov指數是定量描述軌線隨時間推移相互排斥和相互吸引的特征值，而系統的最大Lyapunov指數是判定混沌系統的重要特征.當系統至少有一個Lyapunov指數大于零時，可以判定該系統為混沌系統.

本文根據Jacobian矩陣并采用四階Runge-Kutta算法求得新系統的Lyapunov指數，且λL1=75.026，λL2=-7.563，λL3=-123.345.因為新系統中有一個指數為正值，兩個為負值，所以該新系統為混沌系統.

維數是非線性系統的一個重要幾何特征量，而混沌吸引子具有非整數維數.新系統的Lyapunov維數可以表示為

1+λL1/(-λL2+1)=

1+75.026/(7.563+1)=

9.761 6

(3)

可見，新系統的Lyapunov維數為分數維，從而驗證了該系統為混沌系統.

2 運動區域與功率譜分布

混沌信號與周期信號及穩定收斂信號的功率譜分布不同的原因是由于在生成模型中非線性項決定了系統Jacobian矩陣具有不同特征.通過改變非線性項，非線性系統的運動狀態可以在不同類型之間進行切換，在頻域內表現為混沌信號具有連續功率譜或線狀功率譜.為了實現使功率譜密度集中分布在一定頻域范圍內的目的，利用極限環系統運動軌跡單一且與目標信號相似這一特點，可以在混沌運動狀態和極限環運動狀態之間找到一個平衡點，使得狀態變量限定在一個環狀區域內運動，從而在極限環固有頻率附近產生新的頻譜分量，并最終實現特定頻譜范圍覆蓋.

新系統在Lü混沌系統上增加了非線性約束項ax(x2+y2-b)(x2+y2-c)/(x2+y2).通過實驗仿真可以得出參數a影響系統的運動狀態，而參數b、c影響系統的運動軌跡在x-y平面投影的內外半徑.

當參數b=100、c=400保持不變并改變參數a時，通過仿真可知，當a=0時，系統為Lü系統，且其相空間運動軌跡及狀態變量功率譜分別如圖1、2所示.

當參數b=100、c=400保持不變且a∈(0，0.3)時，新系統是發散的，其相空間運動軌跡不能收斂于特定區域.

當參數b=100、c=400保持不變且a∈[0.3，2.26]時，新系統的相空間運動軌跡逐漸接近極限環，且隨著a值的增大，其最大Lyapunov指數從負值逐漸增大，并逐漸接近于零.當a=2.26時，系統的Lyapunov指數λL1=0.186 4，λL2=-7.235 6且λL3=-290.788 8.當a=2.26時，新系統的相空間運動軌跡與功率譜分別如圖5、6所示.

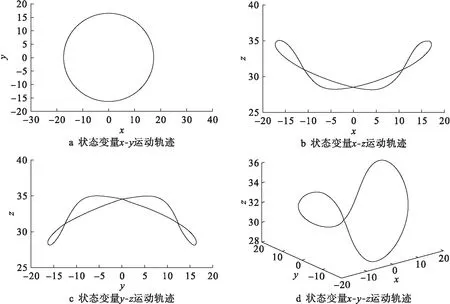
圖5 參數a=2.26時新系統的相空間運動軌跡Fig.5 Phase space motion trajectories of new system with a=2.26

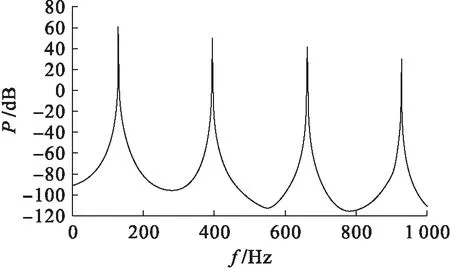
圖6 參數a=2.26時新系統的功率譜Fig.6 Power spectrum of new system with a=2.26

由圖5可見，新系統的相空間運動軌跡在x-y平面的投影接近于正圓.由圖6可見，新系統的功率譜分布于固定頻率附近，但是由于極限環的形狀不理想，因而依然存在諧波分量.

當參數b=100、c=400保持不變且a∈[2.27，2.67]時，新系統逐漸進入混沌狀態，此時可以找到極限環運動與混沌運動之間的過渡點.當a=2.45時，新系統的相空間運動軌跡與功率譜分別如圖7、8所示.觀察圖8可以發現，在新系統的固有頻率附近逐漸產生新的頻譜分量，并呈現出實現目標信號特定頻譜覆蓋范圍的趨勢.當a=2.65時，新系統的相空間運動軌跡與功率譜分別如圖9、10所示.由圖10可見，新系統的功率譜集中分布在一定的頻域范圍內，但依然存在諧波分量.后期可以通過優化極限環的形狀，使得環形軌跡在坐標平面的投影趨近于正圓，從而降低高次諧波所帶來的影響.

3 結 論

本文在Lü系統基礎上，通過增加非線性約束項并進行參數調節，構建新的三維自治混沌系統，并將該新系統的相空間運動軌跡限定在一定的吸引區域內，從而實現特定頻譜范圍覆蓋.通過以上實驗分析可以得出如下結論：

1) 增加非線性項得到的新混沌系統的混沌吸引子的形狀與Lü系統的混沌吸引子完全不同.

2) 混沌信號的功率譜與其相空間運動軌跡密切相關，當需要得到特定頻譜范圍內的混沌信號時，可以通過增加非線性約束項并改變相空間運動軌跡得以實現.

圖7 參數a=2.45時新系統的相空間運動軌跡Fig.7 Phase space motion trajectories of new system with a=2.45

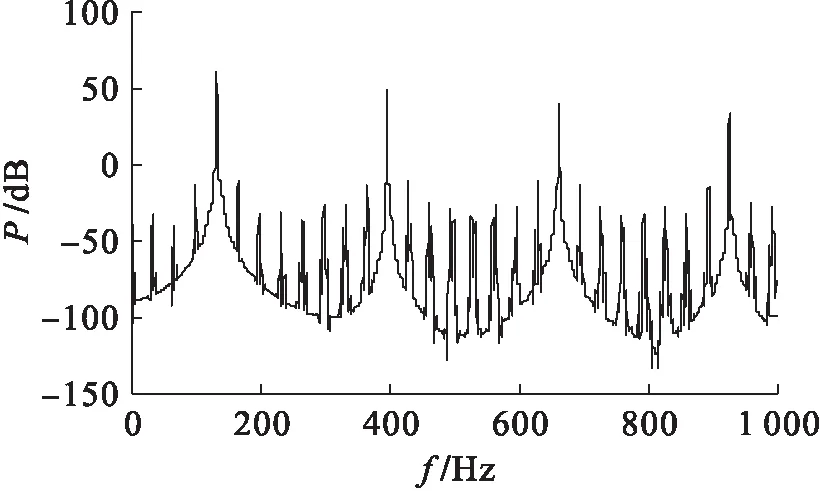
圖8 參數a=2.45時新系統的功率譜Fig.8 Power spectrum of new system with a=2.45

圖9 參數a=2.65時新系統的相空間運動軌跡Fig.9 Phase space motion trajectories of new system with a=2.65

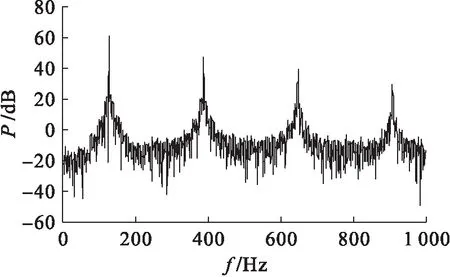
圖10 參數a=2.65時新系統的功率譜Fig.10 Power spectrum of new system with a=2.65