基于ABAQUS的空心方塊裂縫分析

李瑞振，李瑞宇

(1.浙江樹人大學，浙江 杭州 310000；2.亳州市重點工程建設局，安徽 亳州 236000)

1 工程背景

某重力式空心方塊碼頭中的空心方塊，為大體積混凝土結構，其結構尺寸為長6m、寬6m、高8.0m，壁厚0.8m；采用C30普通硅酸鹽水泥，一次性連續澆筑，空心方塊內外表面均采用鋼制模板，底端固定。數值分析中對邊界條件做如下處理：空氣溫度統一取40℃，空氣對流系數取1290.6。混凝土的計算參數見表1。

表1 混凝土性質計算表

試驗采用大型有限元軟件ABAQUS對大體積混凝土空心方塊澆筑后120h內的溫度場進行數值分析計算，本文通過ABAQUS提供的Body heat flux對混凝土水化熱進行賦值，ABAQUS中的Body heat flux功能模塊提供了兩種賦值選項，一種是根據用戶自定義子程序DFLUX進行編程，另一種為常量賦值，本文采用前者編程進行模擬。

2 邊界處理

2.1 澆筑溫度的確定

澆筑溫度Tp可按下式計算：

(1)

式中，T1—入倉溫度；Ta—氣溫；R—太陽輻射熱；β—表面放熱系數；φ1—平倉以前的溫度系數；φ2—平倉以后的溫度系數；τ—從混凝土從入倉到平倉所經歷的時間，min；k—經驗系數。

2.2 水化熱公式確定

混凝土在凝固過程中，水泥會放出大量的熱，俗稱水化熱，水化熱是影響大體積混凝土空心方塊溫度應力的主要因素，目前水化熱公式主要有三種表達方式:

復合指數式：Q(τ)=Q0(1-e-aτb)

(2)

雙曲線式：Q(τ)=Q0τ/(n+τ)

(3)

指數式：Q(τ)=Q0(1-e-mτ)

(4)

式中，Q(τ)—齡期τ時內混凝土累積的水化熱,J/g；Q0—最終水化熱；τ—齡期；a、b、m、n—常數。

由于缺少試驗資料，本文選擇式(2)即復合指數水化熱表達方式。

3 模型試驗

試驗1：環境溫度為40℃，混凝土的入模溫度為20℃。模擬空心方塊內最高溫度和最低溫度隨時間的變化量，空心方塊內累計的水化熱變化量。

上周（11月12日-11月 16日），市場供應偏緊，鉀肥價格穩中有升。11月19日中國氯化鉀批發價格指數（CKPI）為2317.00點，環比上漲11.74點，漲幅為0.51%；同比上漲412.75點，漲幅為21.68%；比基期下跌973.59點，跌幅為29.59%。

試驗2：探究澆筑溫度的變化對空心方塊內最高溫度差的影響，試驗為三組，第一組模型環境溫度為35℃，澆筑溫度分別為30℃、25℃、20℃、15℃、10℃、5℃、-5℃、-10℃；第二組模型環境溫度為25℃，澆筑溫度分別為30℃、25℃、20℃、15℃、10℃、5℃、-5℃、-10℃；第三組模型環境溫度為5℃，澆筑溫度分別為30℃、25℃、20℃、15℃、10℃、5℃、-5℃、-10℃，考慮一次性澆筑，探究澆筑溫度對大體積空心方塊產生的最大溫差的影響，并尋找合理的澆筑溫度。

試驗3：模型試驗澆筑溫度不變，環境溫度改變，試驗分為三組，第一組模型澆筑溫度為35℃，環境溫度分別為30℃、25℃、20℃、15℃、10℃、5℃、0℃；第二組模型澆筑溫度為25℃，環境溫度分別為30℃、25℃、20℃、15℃、10℃、5℃、0℃；第三組模型澆筑溫度為15℃，環境溫度分別為30℃、25℃、20℃、15℃、10℃、5℃、0℃，考慮一次性澆筑，探究環境溫度對大體積空心方塊澆筑過程產生的最大溫差的影響，在某一澆筑溫度下，合理的環境溫度。

4 試驗結果分析

4.1 空心方塊水花熱

為了形象直觀的反應大體積混凝土空心方塊內水泥水化過程隨時間的變化量，將計算結果整理分析得到如圖1—2所示。

圖1 空心方塊內溫度隨時間的變化圖

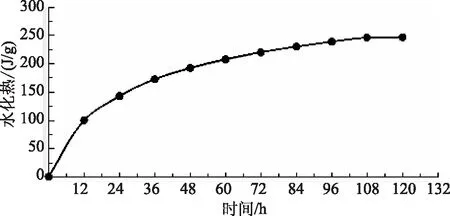
圖2 空心方塊單位體積水化熱隨時間的累積變化圖

由圖1可以看出，大體積混凝土空心方塊水化過程主要集中在0～24h內，0～24h空心方塊內的所能達到最大溫度隨時間增增大而增大，當澆筑后48h，空心方塊內溫度達到最大為55.8℃，隨后隨著時間的增大而減小；0～120h內，空心方塊內的最低溫度隨水泥的水化過程不斷增大；當澆筑后36h時，空心方塊的內外溫差達到最大，為30.9℃此時應做好防護措施，防止空心方塊溫度應力過大，導致空心方塊脹裂。

由圖2可以看出，0～120h內，大體積混凝土空心方塊的水化過程基本結束。單位體積的混凝土產生的水化熱速率隨著大體積混凝土水化過程不斷減小，當混凝土澆筑120h時后，混凝土幾乎不放熱。

將環境溫度降低10℃和澆筑溫度降低10℃，各種工況條件下空心方塊最高溫度仿真結果整理見表3—4。

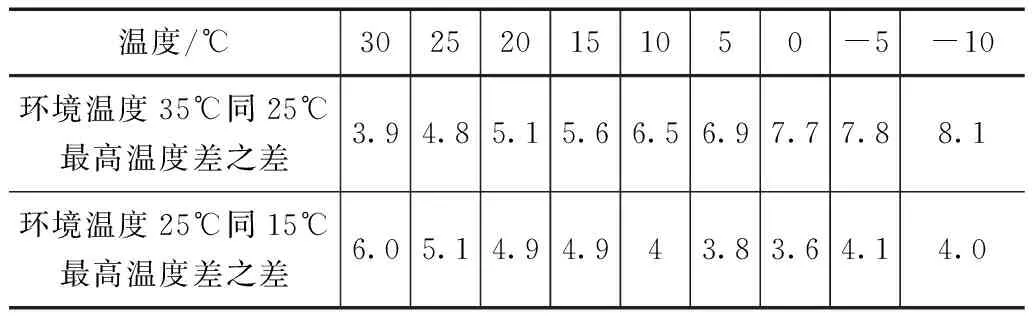
表3 環境溫度相差10℃，空心方塊內最高溫度差

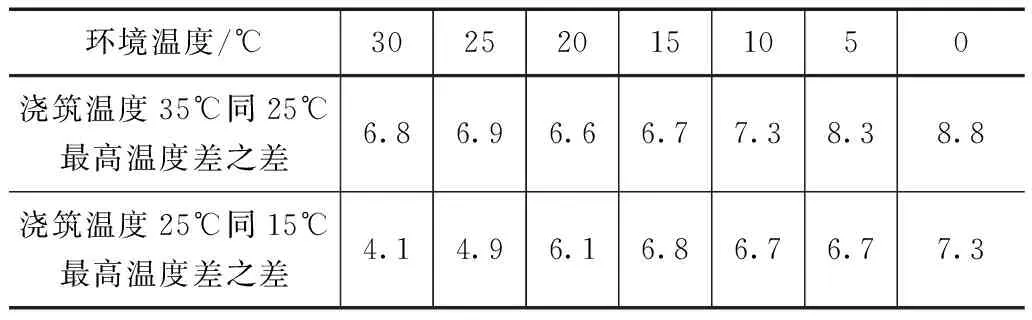
表4 澆筑溫度相差10℃，空心方塊內最高溫度差

由對比可知，同等條件下降低空心方塊的澆筑溫度的效果要好于降低環境溫度溫度，使用同一標號水泥的大體積混凝土空心方塊因水化產生的最高溫度同環境溫度和澆筑溫度有關，且同環境溫度和澆筑溫度成非線性關系，澆筑溫度比環境溫度。

大體積混凝土空心方塊澆筑后水泥的水化是一個極其復雜的過程，混凝土水化放熱在混凝土中形成瞬態溫度場，通過建立有限元模擬水化熱和空氣對流相互作用下的溫度場。仿真結果表明，混凝土從澆筑溫度上升到最高溫度，經歷一個較大幅度的溫升過程，溫度增長主要發生在前期，當澆筑后48h，混凝土內部溫度達到峰值為55.8℃，達到最大后，大體積混凝土空心方塊內最大溫度緩慢下降，到196h基本降至常溫。

4.2 空心方塊的溫度應力

探究此時大體積空心方塊溫度應力大小及應力場分布的影響，其溫度應力變形如圖3—4所示。

圖3 素混凝土外側應力云圖

圖4 素混凝土內側的應力云圖

由圖3可知，空心方塊外側的溫度應力可達到5.386MPa，空心方塊外側的溫度應力主要集中于中間，兩側較小，靠近空心方塊兩端，從上下看，空心方塊兩端最大，中間較大，其他地方應力較小，以XZ為研究平面，由上到下，空心方塊的溫度應力經過由大變小，再變大，再變小，最后再變大的過程；空心方塊內側兩端溫度應力較小，中間溫度應力較大，溫度應力主要集中于空心方塊的內邊角處。

以XZ為研究平面，將空心方塊外側的溫度應力結果整理得到如圖5所示。

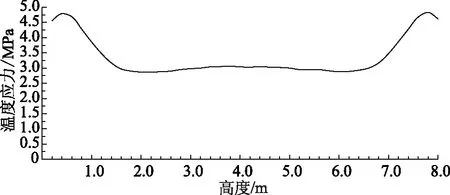
圖5 空心方塊溫度應力隨高度的變化趨勢

由圖5可以看出，空心方塊在溫度荷載下產生的溫度應力主要集中在空心方塊兩端，其他地方變化范圍不大，為3.0MPa左右，最高甚至可達到5.386MPa。

4.3 空心方塊的最大主應力

混凝土是抗壓材料，即可以承受較大的壓應力而不允許產生較大的拉應力，對于混凝土的開裂，若最大主應力(拉應力)大于混凝土的抗拉強度，則認為混凝土開裂。

C30混凝土抗壓應力應變曲線和抗拉應力應變曲線[7]如圖6—7所示。

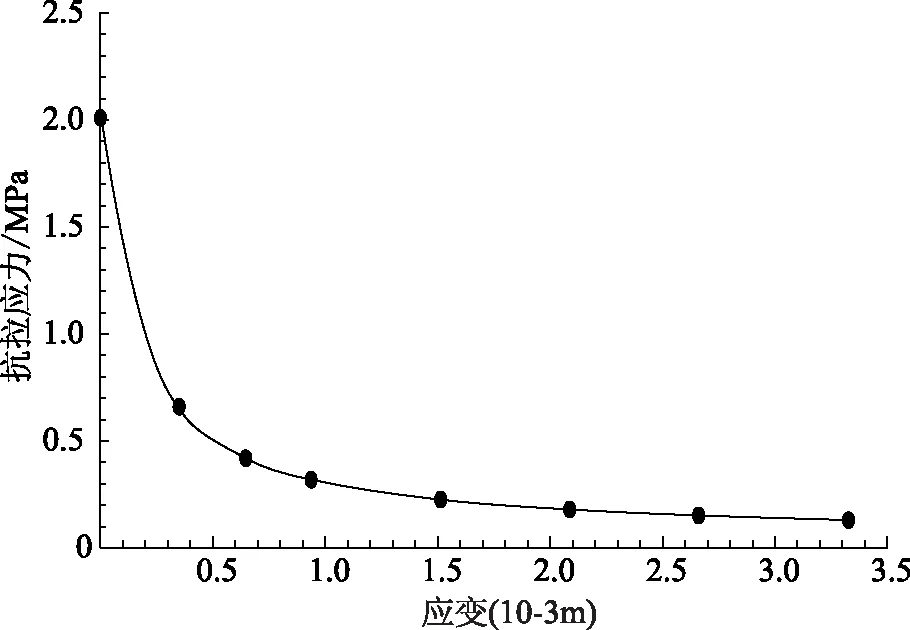
圖7 C30混凝土抗拉應力應變曲線

空心方塊抗壓強度遠大于抗拉強度，對于C30混凝土，當混凝土的壓應力達到15.45MPa時，會產生應變；當混凝土的拉應力達到2.01MPa時，就會產生拉應變。大體積空心方塊澆筑過程中，很容易因水泥的水化過程，導致混凝土產生較大的拉應力，使混凝土發生破壞。

空心方塊內外溫差55.2℃時產生的最大主應力由圖8可知，在溫度荷載下，空心方塊最大主應力可達到5.727MPa，大于C30混凝土產生應變的限制2.01MPa，因此大體積混凝土空心方塊在預制會產生細長裂縫，如果預制過程保護措施不當，這些裂縫會擴展為大裂縫，當裂縫達到某一值后，會導致空心方塊破壞，甚至導致空心方塊碼頭的失穩。

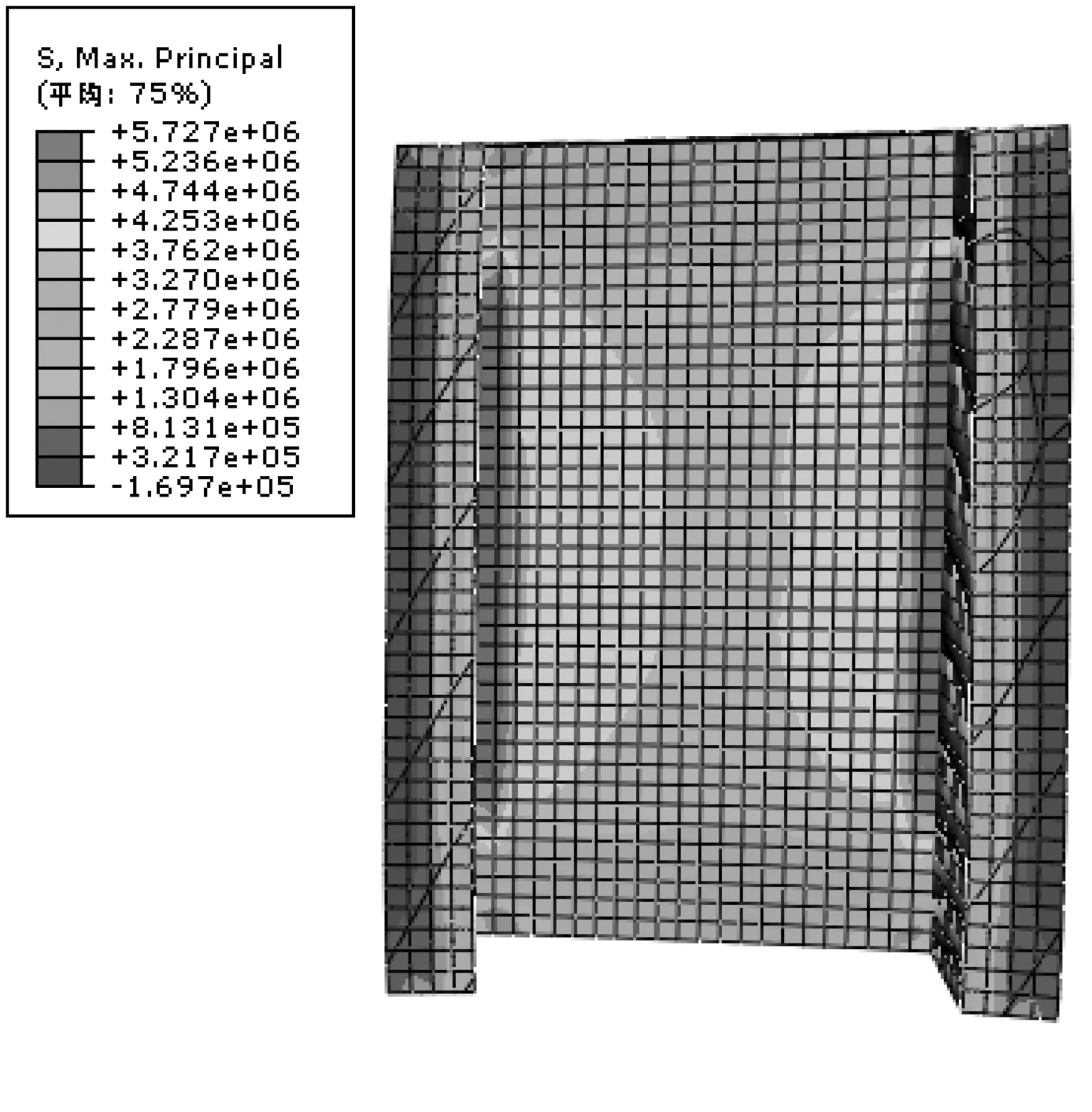
圖8 拉應力分布

5 試驗結論

本文通過不同澆筑溫度和環境溫度條件下的大體積混凝土空心方塊的水化過程仿真模擬，改變澆筑溫度和環境溫度大體積混凝土空心方塊產生的最

大溫差進行對比分析得出：大體積混凝土的水化過程主要發生在前期，預制過程中的環境溫度和澆筑溫度對大體積混凝土的最高溫差均有影響，澆筑溫度的影響要大于環境溫度；預制大體積混凝土的過程中，應盡量選擇低溫環境和低澆筑溫度，環境溫度低，加快了大體積混凝土空心方塊的散熱，素混凝土空心方塊在溫度荷載下會產生很大的主應力，導致空心方塊預制過程中出現細長裂縫，影響空心方塊的質量，應盡量避免。