數學問題解答

2018年11月號問題解答

(解答由問題提供人給出)

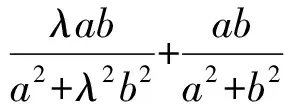
(浙江臺州市洪家高級中學 鄔天泉 318015)

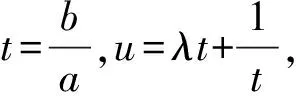
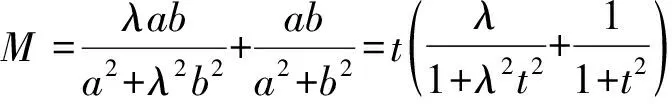
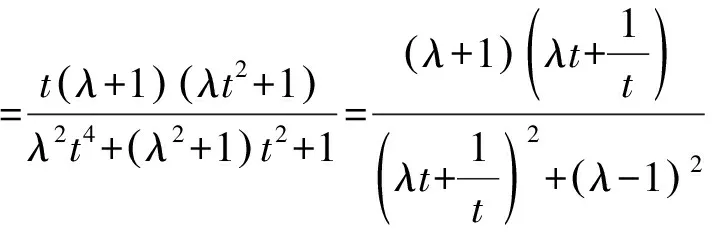
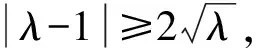
①

當且僅當u=λ-1時①式取等號；

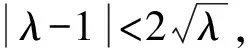
②

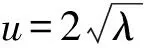
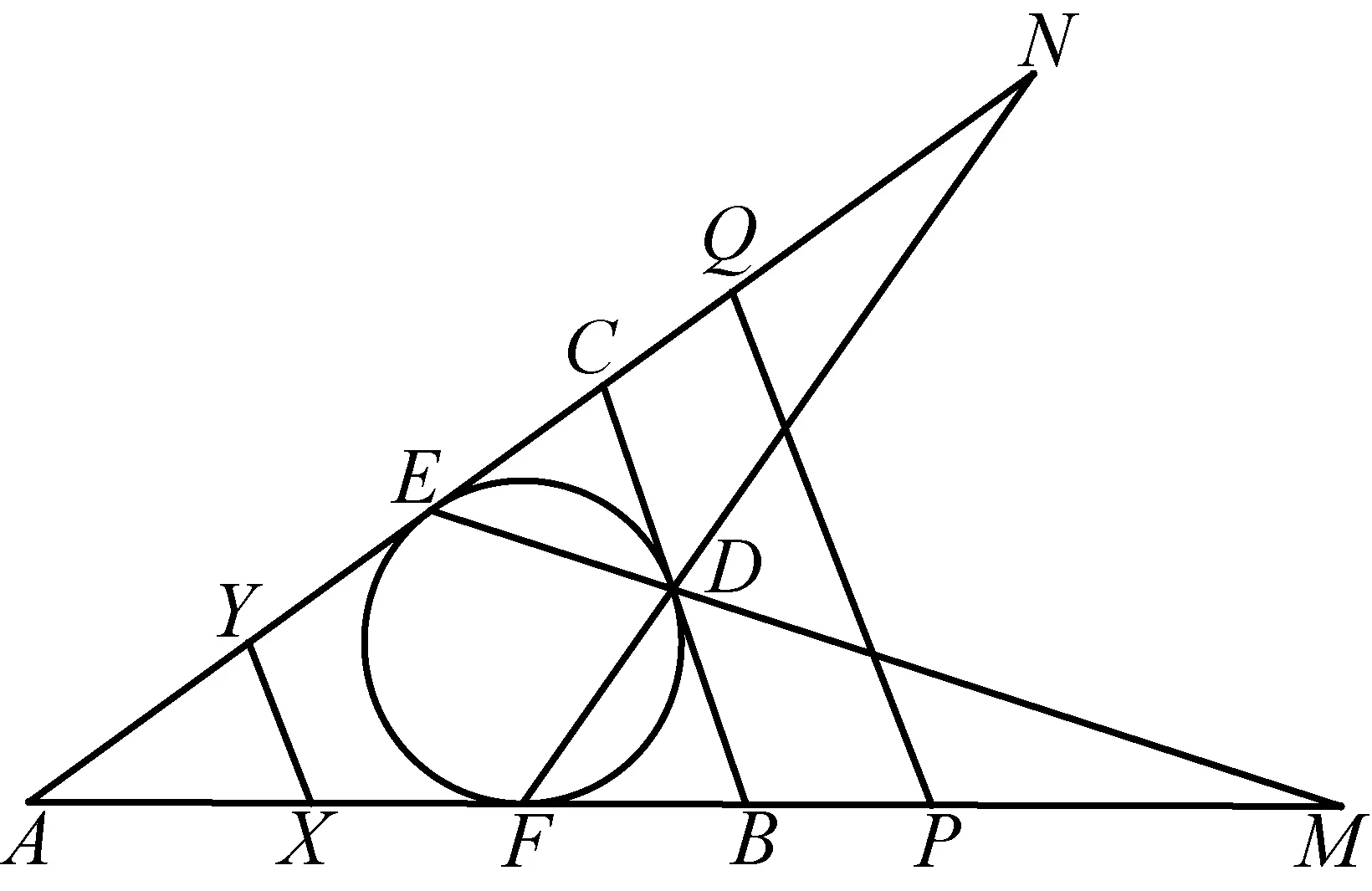
2452如圖，△ABC的內切圓與邊BC，CA，AB分別切于點D，E，F，線段ED和AB延長后交于點M，線段FD和AC延長后交于點N，點P，Q分別為線段FM，EN的中點，點X，Y分別在邊AB，AC上且滿足XB=YC=BC，證明：XY∥PQ.

(河南省輝縣市一中 賀基軍 453600)

證明引理：如果平面上四點G，H，V，W滿足GV2-HV2=GW2-HW2，那么GH⊥VW.

用解析法給出引理證明：以點G為原點建立直角坐標系，使點H不在坐標軸上.設各點的坐標為H(x1，y1)，V(x2，y2)，W(x3，y3)，其中x1≠0，y1≠0.

因GV2-HV2=GW2-HW2，

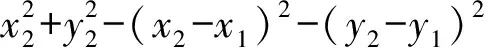
即y1(y3-y2)=-x1(x3-x2).

如果x3-x2= 0，則y3-y2= 0，

此時V，W重合為一點，這與已知條件不符，

因此x3-x2≠0.

在原題中(如圖)，根據正弦定理得

因∠BDM=∠CDE=∠CED=180°-∠AEM，

故sin∠BDM=sin∠AEM，

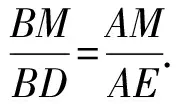
將BF=BD，AF=AE代入上式得

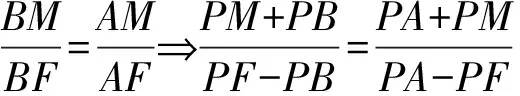
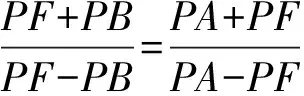
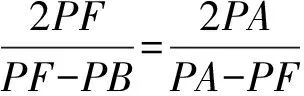
?PB·PA=PF2.

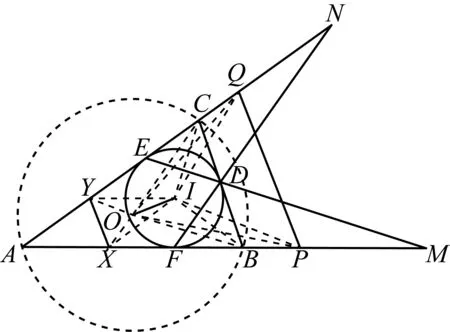
設△ABC的外接圓為圓O，內切圓為圓I，它們的半徑分別為R，r.連接OI及PO，PI，QO，QI.

根據切割線定理得

PO2-R2=(PO-R)(PO+R)=PB·PA，

由PB·PA=PF2得PO2=PF2+R2，

同理QO2=QE2+R2.

因此PO2-QO2=PF2-QE2

=(PF2+r2)-(QE2+r2)

=PI2-QI2，

根據引理得PQ⊥OI.

連接XO，XI，YO，YI及OB，OC，IB，IC.

根據余弦定理得

XO2=XB2+OB2-2XB·OBcos∠XBO，

YO2=YC2+OC2-2YC·OCcos∠YCO.

因XB=YC=BC，OB=OC，

故

XO2-YO2=2BC(OCcos∠YCO-OBcos∠XBO)

在△XIB中，再由余弦定理得

XI2-BI2=BX2-2BI·BXcos∠IBX，

由∠YCI=∠BCI，YC=BC得YI=BI.

因此XI2-YI2=XI2-BI2

=BX2-2BI·BXcos∠IBX

=BC(BC-2BIcos∠IBX)

=BC(BC-2BF)

=BC[BC-(AB+BC-AC)]

=BC(AC-AB)=XO2-YO2，

根據引理得XY⊥OI，

由PQ⊥OI得XY∥PQ.證畢.

2453已知a、b、c為正實數，試證：

(*)

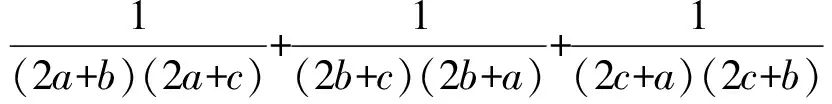
(浙江湖州市雙林中學 李建潮 313012)

證明記

∑(2a+b)(2a+c)(b+c)2=(2a+b)(2a+c)(b+c)2+(2b+c)(2b+a)·(c+a)2+(2c+a)·(2c+b)(a+b)2．

則由柯西不等式

≥(x1y1+x2y2+x3y3)2，

有

≥∑(b+c)2=4∑a2，

①

而

(2a+b)(2a+c)(b+c)2

=(2a+b)(b+c)·(2a+c)(b+c)

=2∑bc+b(b-c)2∑bc-c(b-c)

=4(∑bc)2+2(b-c)2∑bc-bc(b-c)2

≤2∑bc2∑bc+(b-c)2，

從而

∑(2a+b)(2a+c)(b+c)2

≤2∑bc6∑bc+∑(b-c)2

=2∑bc(2∑a2+4∑bc)

=4∑a2∑bc，

②

聯立①與②二式，有

即

(*)

即為所證.

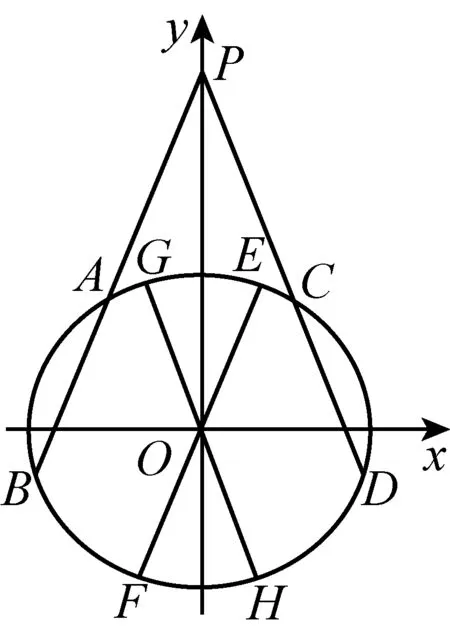
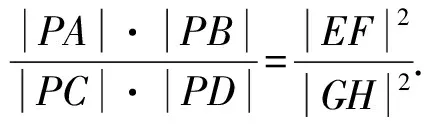
(安康學院數學與統計學院 趙臨龍 725000)

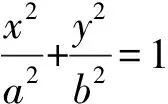
對于直線PAB，由直線方程

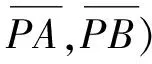
(1)

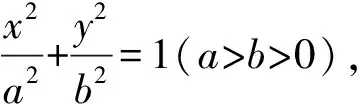
(2)

得到

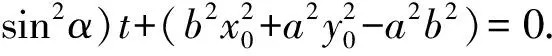
(3)

當點P在橢圓Γ外部時，t1t2>0，則

(4)

當點P在橢圓Γ內部時，t1t2<0，則

(5)

于是，對于不在橢圓Γ上的點P，有

(6)

同理，對于不在橢圓Γ上的點P，直線PCD有結論

(7)

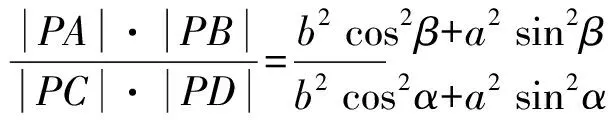
(8)

此時，在方程(3)中，令x0=0,y0=0，

即傾斜角為α的直徑EOF，滿足關系

(9)

即直徑EOF長度為

(10)

同理，求得直徑GOH長度為

(11)

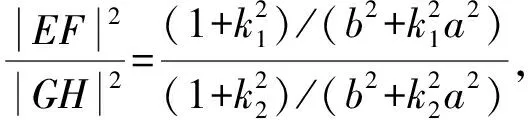
(12)

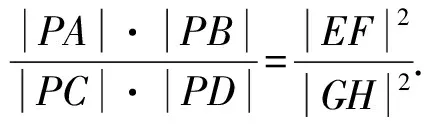
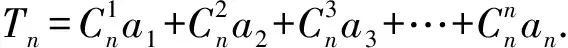
(江蘇省啟東市匯龍中學 倪紅林 226200)

解因為a1=1，a2=1，

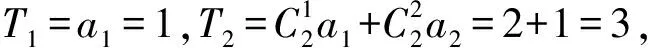
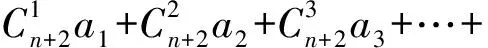
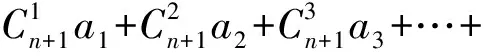
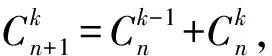
所以

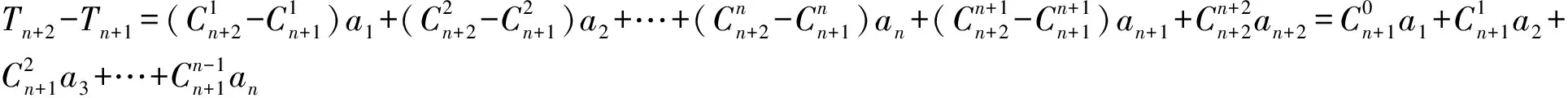
所以

由a1=a2=1，an+2=an+1+an,n∈N*，

所以

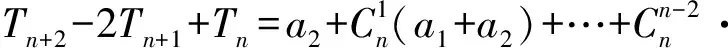
所以Tn+2-2Tn+1+Tn=Tn+1，

即Tn+2=3Tn+1-Tn，(n∈N*)

因此Tn+2除以8的余數,完全由Tn+1，Tn除以8的余數確定，

又T1=1，T2=3，

所以T3=3T2-T1=9-1=8，

T4=3T3-T2=24-3=21，

T5=3T4-T3=63-8=55，

T6=3T5-T4=165-21=144，

T7=3T6-T5=432-55=377，

T8=3T7-T6=1131-144=987，

T9=3T8-T7=2961-377=2584，

由以上計算及Tn+2=3Tn+1-Tn,n∈N*可知,數列Tn各項除以8的余數依次是1,3,0,5,7,0,1,3,0,5,7,0,…，它是一個以6為周期的數列，從而Tn除以8的余數為0的正整數n，等價于n除以3的余數為0的正整數n，

所以n=3k,k∈N*，

即所求集合為: {n|n=3k,k∈N*}

2018年12號月問題

(來稿請注明出處——編者)

2456已知a1,a2,…,an>0(n≥2)，求證：

(浙江省海鹽縣元濟高級中學 張艷宗 314300；北京航空航天大學圖書館 宋慶 100191)

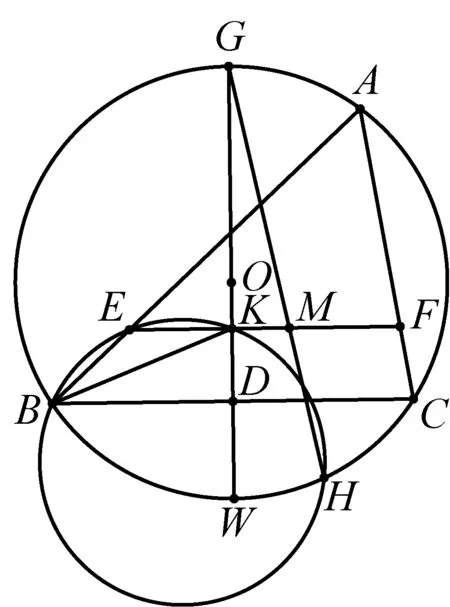
2457如圖，E、F分別在△ABC的AB、AC上，且EF∥BC，過BC中點D作DG⊥BC交△ABC的外接圓O于G和W，交EF于K，△BEK的外接圓交⊙O于H，GH交EF于M，求證：A、M、W三點共線．

(江西師范高等專科學校 王建榮 335000)

2458在△ABC中,求證

(天津水運高級技工學校 黃兆麟 300456)

2459設點I,Ia,Ib,Ic分別為△ABC的內心和旁心，R為其外接圓的半徑，證明：6R≥IIa+IIb+IIc.

(安徽省樅陽縣宏實中學 江保兵 246700)

2460在三角形ABC中，記BC=a,CA=b,AB=c，n∈N+且n≥2，0<λ≤1,

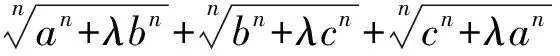
(安徽省岳西中學 儲百六 246600)