時變時滯系統的L-K泛函

孫 欣, 高 躍

(沈陽師范大學 數學與系統科學學院, 沈陽 110034)

0 引 言

時滯系統的分析和綜合一直以來是控制理論和控制工程領域研究的熱點問題。自20世紀70年代 Lyapunov泛函引入時滯系統的分析設計以來,Lyapunov方法已經成為處理時滯系統的有利工具。基于Lyapunov穩定性理論,構造一個適合的Lyapunov-Krasovskii泛函(簡稱L-K泛函)得到時滯系統穩定性條件是分析和綜合時滯系統常采用的方法。

一般地,由構造的L-K泛函得到的是時滯系統穩定的充分條件。目前,L-K泛函仍沒有統一的構造方法。在構造L-K泛函時,通常含有積分項,從一重積分、二重積分逐漸發展為三重積分和四重積分。2010年,SUN等[1]提出將三重積分加入到L-K泛函中,有效降低了保守性。

同時, 因對積分項的放大而利用的不等式隨之增多,形式不一。Xia 等[2]、孫等[3]文獻中,積分項的放大均采用了Jensen積分不等式。文獻[4]提出了Wirtinger積分不等式在時滯系統中的應用,相比Jensen積分不等式,Wirtinger積分不等式具有更小的保守性。

本文在對現有時滯系統研究成果的基礎上,對L-K泛函的構造形式、L-K泛函求導后積分項處理這2方面做以分類、對比與總結。

1 構造L-K泛函

在穩定性判據推導過程中,需要構造一個合適的L-K泛函來獲得系統穩定性條件。對于同一個時滯系統, L-K泛函的選取也不相同,因此得到的穩定性判據形式不同,結果的保守性也有差異。本文將針對時變時滯系統常用的3類泛函進行研究。

1.1 問題描述

考慮時變時滯系統

(1)

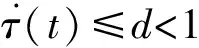
1.2 3類常用的L-K泛函

對于時滯系統而言,常用的L-K泛函包括雙重積分型、三重積分型、四重積分型和增廣型。

1.2.1 雙重積分型L-K泛函

文獻[5]針對區間時變時滯系統,選取了如下形式的L-K泛函:

其中:Qi>0,Wi>0,R>0,P,Qi,Wi,(i=1,2),R為正定矩陣;x(t)是為狀態向量。 由式(2)可以看出,V3(t)為雙重積分型, 對V3(t)關于t求導,得

(3)

1.2.2 多重積分型L-K泛函

針對雙重積分型 L-K泛函時滯信息有限的問題,現已擴展到多重積分型,其中包括三重積分型和四重積分型。

1) 三重積分型L-K泛函

文獻[1]提出將三重積分加入到L-K泛函中,文獻[6-8]在 L-K 泛函中也加入了三重積分項,形式如下:

(4)

其中Ui>0(i=1,2)為正定矩陣。

2) 四重積分型L-K泛函

文獻[9] 在L-K泛函中加入四重積分, 具體形式如下:

(5)

其中Zi>0(i=1,2)為正定矩陣。

1.2.3 增廣型L-K泛函

文獻[3]在構造L-K泛函時,對狀態向量進行擴維,得到增廣型。形式如下:

V(t)=V1(t)+V2(t)+V3(t)+V4(t)

其中

(6)

其中:R,T,Q>0為正定矩陣;P為非奇異矩陣;Y為適維矩陣。

這里V4(t)狀態向量是增廣型。分別對V3,V4關于t求導,得

1.3 L-K泛函中時滯信息的處理

在推導時變時滯系統穩定性條件,構造L-K泛函時,通常要考慮時變時滯上下界τM,τm信息,不僅如此,還將時變時滯τ(t)的變化區間[τm,τM]分割成N(N≥2)部分,這種處理方法稱為時滯分割法。根據情況,時滯可以進行均等分割,若考慮一般化情況,時滯還可以進行不均等分割。

1.3.1 時滯均等分割

其中

其中:Qi>0(i=1,…,4),Tj>0(j=1,2)為正定矩陣。

可以看到V函數中不僅含有時滯下限τm和時滯上限τM,還有中值τ0。取中值的目的在于構造L-K泛函時另外增加了時滯中值的信息, 降低結論保守性。

1.3.2 時滯不均等分割

時滯不均等分割較均等分割更具一般性,可以利用更多時滯信息,降低結論保守性。以文獻[9]為例,考慮時變時滯系統(1),運用時滯不均等分割方法構造L-K泛函。引入一個自由參數γ滿足0<γ<1。變時滯h(t)滿足hm≤h(t)≤hM,設hΔ=γhm+(1-γ)hM,則有hm

2 L-K泛函求導后積分項的處理方法

為了得到時滯系統穩定性條件,首先構造L-K泛函,然后對泛函求導。在求導過程中,為保證穩定性條件可以表示成線性矩陣不等式的形式, 方便利用MATLAB中LMI工具箱求解,需要處理L-K泛函求導后的某些積分項。或者進行恒等變形,例如引入自由權矩陣;或者進行放大,放大過程中,會選用不同形式的不等式,如Jensen積分不等式、Wirtinger積分不等式等。運用這些不等式時,相應會產生一定的保守性。

2.1 自由權矩陣方法

對泛函L-K求導后,可以通過增加矩陣變量構造恒為零的等式,以減少結論保守性,這種方法稱為自由權矩陣方法。文獻[5]中,添加了恒為零的等式:

自由權矩陣方法的優點在于,它沒有改變原式大小,通過引入自由矩陣變量,降低結論保守性。

2.2 Jensen積分不等式

Gu等[10]提出了以下形式的Jensen積分不等式:對于向量函數x以及正定矩陣R>0,有積分不等式成立:

(7)

通過Jensen積分不等式,可以把不等式左邊積分項含有的二次型轉化成不等式右邊2個向量相乘的形式,從而可以寫成線性矩陣不等式的形式。還可以推廣到二重積分或三重積分的情形。

(二重Jensen積分不等式)[11]:對于向量函數x以及正定矩陣R,以下積分不等式成立:

(8)

還有許多改進的Jensen積分不等式的運用,如文獻[3,10-13]。

2.3 Wirtinger積分不等式

Wirtinger積分不等式是傅里葉分析中很著名的不等式,根據限定條件的不同,分為多種形式。與Jensen積分不等式相比,它具有更小的保守性。Wirtinger積分不等式的運用,可見文獻[11,14-17];其離散形式的運用,可見文獻[18-20]。

Wirtinger積分不等式[4]:對任意給定的常矩陣R>0,向量函數x:[a,b]→Rn,有如下不等式成立:

(9)

其中

(10)

注釋2 比較式(7)、式(9),可以看到Wirtinger積分不等式比Jensen積分不等式保守性小。

Wirtinger積分不等式還有一些其它形式[11]:對任意的正定矩陣R>0,向量函數x:[a,b]→Rn,有如下不等式成立:

其中

Wirtinger積分不等式適用于連續時滯系統。與連續時滯系統對應的是離散時滯系統,那么離散型的Wirtinger不等式[18-19]可以應用到離散時滯系統中, 關于離散型的Wirtinger不等式有如下形式:

1) 對于給定的正定矩陣R>0,非負整數a,b,k滿足a≤b≤k,x(s)為列向量函數,有如下不等式成立:

其中

其中

3 結 語

本文研究了時變時滯系統L-K泛函的構造和泛函求導后積分項的處理方法。L-K泛函包括雙重積分型、多重積分型、增廣型,以及利用時滯分割法構造L-K泛函。L-K泛函求導后積分項的處理方法,有自由權矩陣法、Jensen積分不等式和Wirtinger積分不等式方法。較Jensen積分不等式、Wirtinger積分不等式有更小的保守性。