正弦變換混沌系統及性能分析

田小平, 高曉蕓, 吳成茂

(西安郵電大學 電子工程學院, 陜西 西安 710121)

混沌系統是非線性系統里的一類特殊動力系統，對給定的初始輸入會產生復雜的、偽隨機的、長期不可預測的輸出。混沌系統在生物、醫學、物理、工程和技術等多個交叉學科領域有重要的應用價值[1]。在一些情況下，混沌的無序性、混亂性、偽隨機性和初始值高度敏感性是有用的，比如在流體混合、生物系統、保密通信等方面。另一方面，混沌系統具有的遍歷性、偽隨機性、有界性、對初始值高度敏感性，使得混沌系統生成的偽隨機序列很適合于信息加密，具有良好的擴散和混亂效果[2]。生成適當的混沌系統尤為重要。

目前，大量的研究致力于抵消混沌退化和提高現有混沌系統的性能。這些工作主要分為兩個方面，一方面是用不同方法干擾現有混沌系統信號，如文獻[3]提出了一種利用已有的混沌映射獲取新混沌映射的輪切換系統，但生成的新混沌映射的混沌性能有限，不具有魯棒性[4]。文獻[5]引入了一個參數控制混沌系統來生成新的混沌映射，生成的混沌映射一些具有好的魯棒性，而有的則混沌性能比較差，不具有穩定性[6]。另一方面，是設計具有更好混沌性能的新混沌系統。與混沌系統的信號干擾技術相比，新混沌系統的產生可以更好地促進基于混沌的實際應用，但也具有一定的局限性。如文獻[7]提出了一個新的一維混沌系統，可以生成具有魯棒性的新混沌映射，其中包含的模塊化操作，使得解析該混沌映射的性能較困難[8]。

為了改善經典Logistic、Sine和Tent等映射僅在小范圍內具有混沌行為且復雜性低等不足，本文擬提出一種基于正弦變換的混沌系統(sine-transform-based chaotic system，STBCS)作為一維混沌映射的一般框架。該方法首先對現有混沌映射的輸出進行線性加權組合，再對組合結果進行正弦函數變換并產生新的映射。最后利用Logistic、Sine和Tent三個經典混沌映射構造3個新的混沌例子，通過分叉圖和Lyapunov指數法檢驗該類映射具有的混沌性和魯棒性，并對該類映射產生序列所對應的樣本熵和Kolmogorov熵進行測試，以分析其復雜性和不可預測性。

1 經典的Logistic、Sine和Tent混沌映射

Logistic映射、Sine映射和Tent映射是常見的三種經典的混沌系統，它們將被用作種子映射來生成新的混沌映射。

Logistic映射可以在一定范圍內存儲和折疊變量，在[0,1]范圍內輸出一個變量[9]。理論上，Logistic映射可以定義為

xi+1=L(xi)=4rxi(1-xi)。

(1)

其中，動態系統的輸入為xi，輸出為xi+1(i=0,1,2,…)；L(xi)表示Logistic映射；r是控制參數。

Sine映射是由正弦函數派生的正弦映射，它將[0,1/π]范圍內的輸入角度轉換到一定范圍內輸出[10]。正弦映射的數學模型為

xi+1=S(xi)=rsin (πxi)。

(2)

其中S(xi)表示Sine映射。

Tent映射根據其范圍拉伸或折疊輸入變量，如果輸入小于0.5，則延長輸入；否則折疊輸入[11]。Tent映射可以定義為

(3)

其中T(xi)表示Tent映射。

通過系統分叉圖和系統的Lyapunov指數2個指標可以確定1個系統是否處于混沌狀態。分叉圖用于描述動態系統的輸出范圍及其隨參數的變化，正的Lyapunov指數表示存在混沌行為[11]。Logistic映射出現混沌行為的區間為[3.57,4]，占整個區間的比例為10.75%；Sine映射出現混沌行為的區間為[3.40,4]，占整個區間的比例為15%；Tent映射出現混沌行為的區間為[0.40,1]，占整個區間的比例為60%。

2 正弦變換混沌映射

2.1 基于正弦變換混沌系統構造方法

基于正弦變換混沌系統構造原理，如圖1所示。

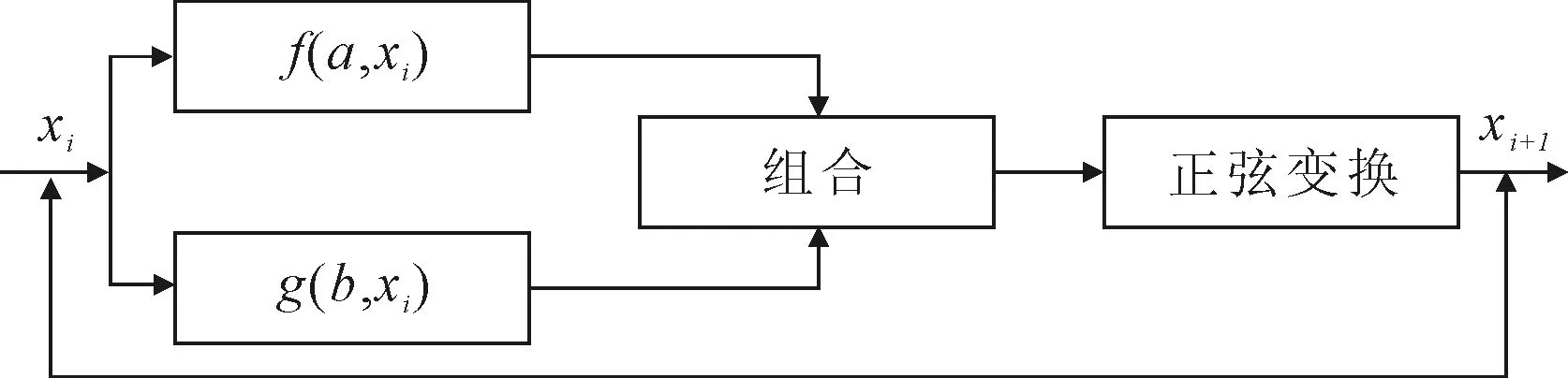
圖1 基于正弦變換混沌系統構造的原理

圖1中，f(a,xi)和g(b,xi)分別是具有控制參數a和b的2個種子映射，該組合能線性地組合2個種子映射的輸出，正弦變換對組合的結果執行非線性變換。在每次迭代中，輸入xi被同時反饋到f(a,xi)和g(b,xi)中，然后對f(a,xi)和g(b,xi)的組合輸出進行正弦變換。

設N(xi)表示所提出的STBCS，其定義為

xi+1=N(xi)=sin (π(f(a,xi)+g(b,xi)))。

(4)

任何現有的一維混沌映射都可以用作STBCS的種子映射。用戶可將種子映射f(a,xi)和g(b,xi)設置為相同或不同的混沌映射。

(1) 當f(a,xi)和g(b,xi)是相同的一維混沌映射時，STBCS可表示為

xi+1=sin (π(f(a,xi)+f(b,xi)))。

(5)

或者

xi+1=sin (π(g(a,xi)+g(b,xi)))。

(6)

在該STBCS系統中，2個不同控制參數混沌映射輸出線性組合，而并非線性變換以獲得更復雜的混沌行為，STBCS的混沌性降低。

(2) 當所選f(a,xi)和g(b,xi)是2個不同的一維混沌映射時，STBCS定義在式(4)具有交換性。交換其2個種子映射f(a,xi)和g(b,xi)的位置，STBCS會生成相同的混沌映射。STBCS系統提供了很大的靈活性，使用不同的f(a,xi)和g(b,xi)可以生成大量新的混沌映射。這些新的混沌映射和它們所對應的種子映射完全不同，具有更復雜的混沌行為。

此外，圖1所表示的STBCS結構可以進一步擴展為3個或更多個種子映射。對于N個種子映射的STBCS系統擴展原理如圖2所示。

圖2 具有N個種子映射的STBCS原理

圖2中，每一次迭代會將輸入xi同時反饋到N個種子映射中，即f1(a1,xi),f2(a2,xi),…,fN(aN,xi),并且對所有種子映射的輸出進行正弦變換，這為選擇種子映射提供了靈活性，生成的混沌映射具有更復雜的混沌行為和參數設置，因此它們具有更好的混沌性能，并產生更多的隨機、不可預測的輸出序列。然而利用更多的種子映射可能會帶來許多一些負面影響，比如時間延遲，實施困難和分析復雜的問題。

2.2 Lyapunov指數法分析混沌行為

在所有確定混沌行為的方法中，Lyapunov指數是重要的、被廣泛接受的指標之一[12]。對于初始狀態稍有不同的相同混沌系統的2條軌跡，Lyapunov指數測量它們的平均指數散度。對于1個可微分的一階差分方程xi+1=f(xi)，Lyapunov指數可以定義為

(7)

負的Lyapunov指數意味著它們軌跡的距離減小，并且隨著時間的推移，它們將最終重疊，從而能識別周期性行為。正的Lyapunov指數表示初始狀態略有不同的動力系統的2個軌跡在每個單位時間內呈指數分布，隨著系統演化它們將完全不同，從而可以識別混沌行為。如果λf(x)>0，則認為動態系統xi+1=f(xi)具有混沌行為。

為了分析式(4)所對應的STBCS混沌行為，需要首先使用1個中間方程來表示2個種子映射的組合。定義STBCS種子映射的組合為

H(xi)=f(a,xi)+g(b,xi)，

則STBCS的定義式可以重寫為

xi+1=N(xi)=sin (πH(xi))。

(8)

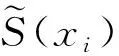
(9)

根據式(7)中Lyapunov指數的定義，可以得到STBCS的Lyapunov指數為

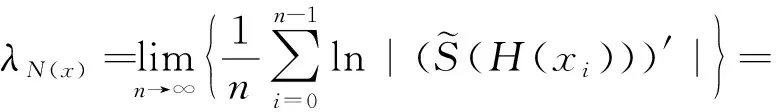
(10)

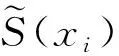
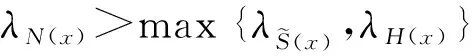
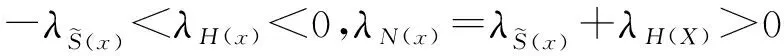
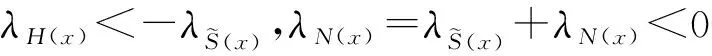
如果一階方程H(x)是混沌的，那么STBCS總是混沌的，它比H(x)和參數r=1對應的正弦映射都具有更好的混沌性能；如果H(x)不是混沌的，則STBCS也有混沌行為。STBCS是一個通用的框架，STBCS混沌行為的穩健性不能直接分析，穩健混沌行為的分析通常適用于有特定表達式的混沌映射。

2.3 新型混沌系統產生的3個例子

使用提出的STBCS，可以設置不同的一維混沌映射f(a,xi)和g(b,xi)作為種子映射以生成大量新的混沌映射。為了顯示STBCS的有效性，將分析以3個現有的一維混沌映射生成的3個新型混沌映射。為了簡單起見，取控制參數a、b分別為r和1-r，并按3種不同的方式加以設置。

(1) Logistic-Sine(LS)映射

當選擇種子映射f(a,xi)為Logistic映射，g(b,xi)為Sine映射時，可以生成1個新型混沌映射，即Logistic-Sine(LS)映射。將其控制參數a、b分別設置為r和1-r時，獲得的LS映射可定義為

xi+1=sin(π(L(r,xi)+S(1-r,xi)))= sin(π(4rxi(1-xi)+(1-r)sin(πxi)))。

(11)

(2) Logistic-Tent(LT)映射

當選擇種子f(a,xi)為Logistic映射，g(b,xi)為Tent映射時，可以生1個新型混沌映射，即Logistic-Tent(LT)映射。將其控制參數a、b分別設置為r和1-r時，對應的LS映射可定義為

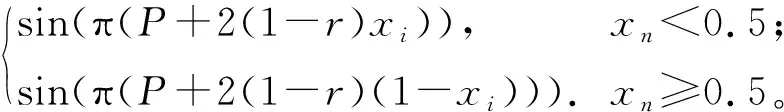
(12)

其中，P=4rxi(1-xi)。

(3) Tent-Sine(TS)映射

當選擇種子映射f(a,xi)為Tent映射，g(b,xi)為Sine映射時，可以生1個新型混沌映射，即Tent-Sine(TS)映射。將其控制參數a、b分別設置為r和1-r時，對應的LS映射可定義為

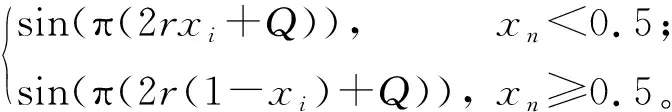
(13)

其中，Q=(1-r)sin(πxi)。

3 實驗結果及分析

為了驗證本文所提出的STBCS系統可以生成具有更好混沌性能的新混沌映射。擬評估由STBCS生成的3個新的混沌映射，并將這些新的混沌映射與其相應的種子映射進行比較。具體從分叉圖、Lyapunov指數、樣本熵(sample entropy, SE)[13]和Kolmogorov熵[14]4個方面進行分析。

3.1 混沌性和魯棒性分析

分叉圖用于描述動態系統的輸出范圍及其隨參數的變化，不僅能揭示系統不同狀態之間的聯系和轉化，也是研究失穩和混沌產生的機理和條件的重要途徑，分叉與系統的結構穩定有著十分密切的聯系。LS映射、LT映射、TS映射隨著其控制參數r變化的分叉圖，如圖3所示。

(a) LS映射的分叉圖

(b) LT映射的分叉圖

(c) TS映射的分叉圖

從圖3可以看出，LS、LT、TS映射的分叉圖均隨機均勻分布在所有參數范圍內，占整個區間的100%，表明新產生的3個混沌映射在整個參數范圍內具有魯棒性的混沌行為。

運用Lyapunov指數進行比較說明，更能突出問題。Lyapunov指數是定量描述這一現象的量，即衡量系統動力學特性的一個重要定量指標，表征了系統在相空間中相鄰軌道間收斂或發散的平均指數率。對于系統是否存在動力學混沌，可以從最大Lyapunov指數是否大于零直觀地判斷出來，只要存在一個正的Lyapunov指數，就說明系統處于混沌狀態，且Lyapunov指數正值越大表示性能越好。LS、LT、TS映射以及它們種子映射的Lyapunov指數，如圖4所示。

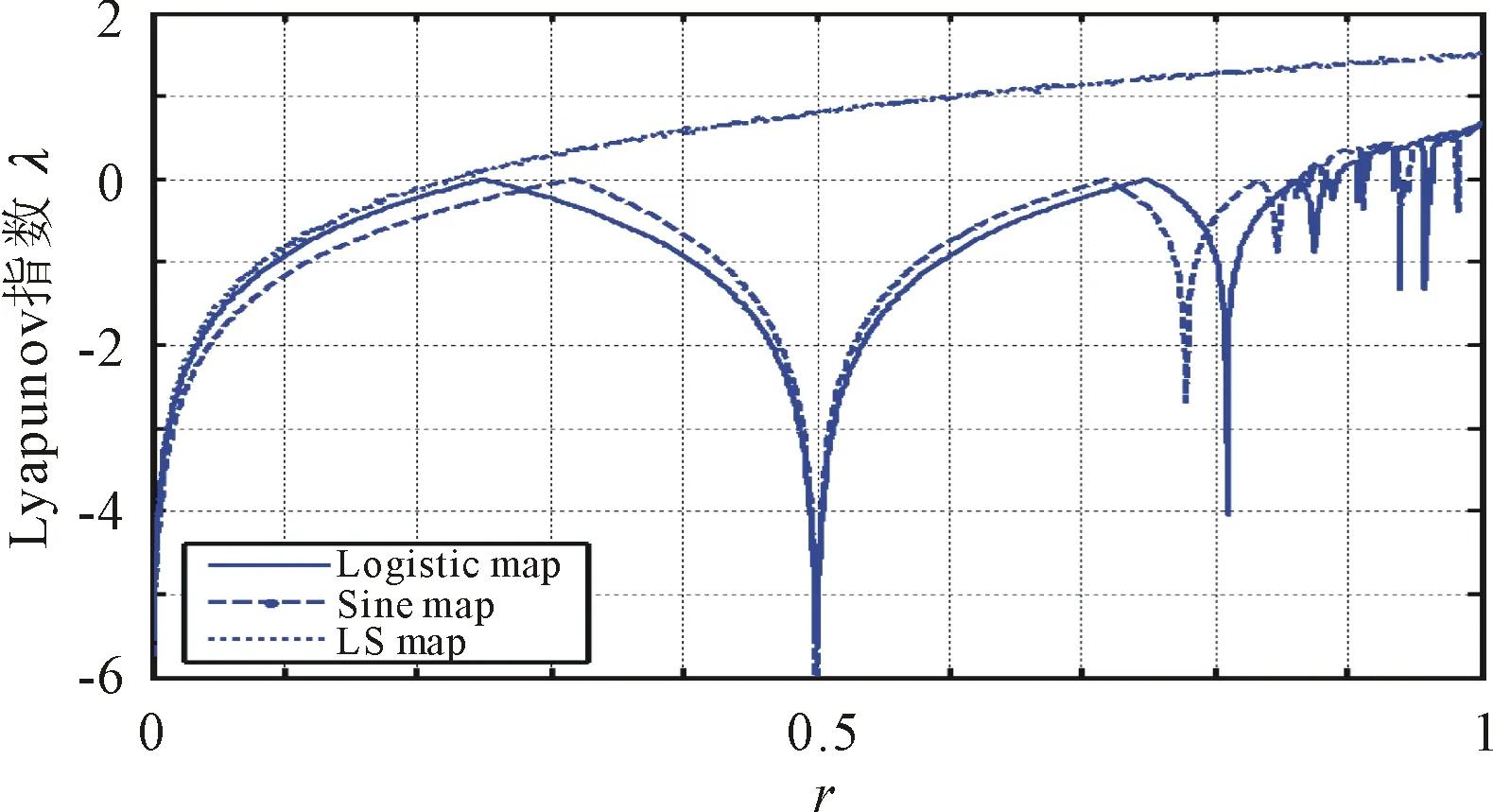
(a) LS映射及其種子映射的Lyapunov指數

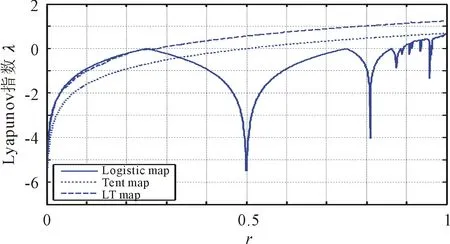
(b) LT映射及其種子映射的Lyapunov指數

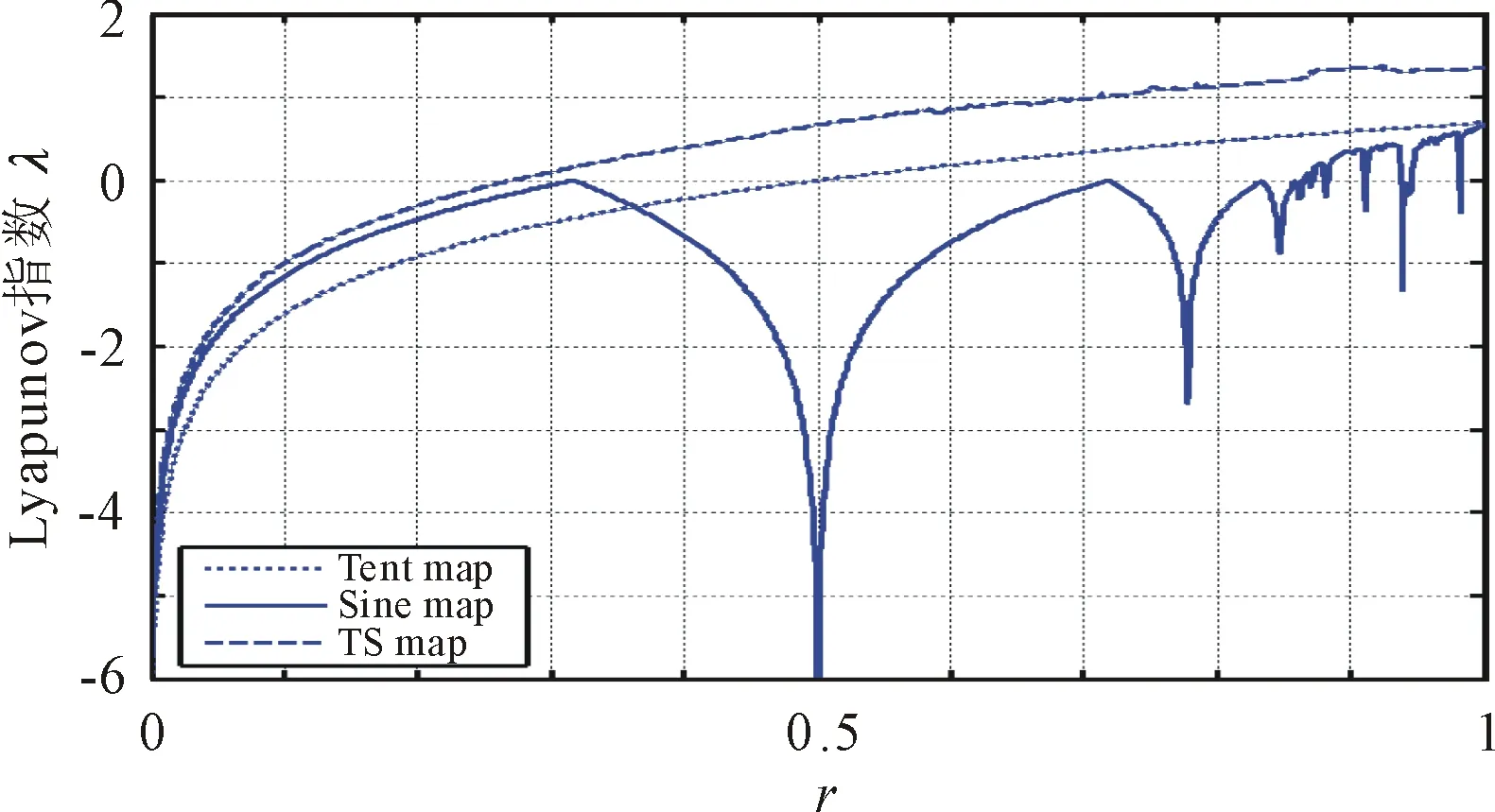
(c) TS映射及其種子映射的Lyapunov指數

從圖4中可以看出，種子映射僅在少數的參數范圍內具有正Lyapunov指數，由所提出的STBCS方法生成的新混沌映射的Lyapunov指數在參數r∈[0.25,1]范圍內均為正，這意味著新的混沌映射在參數r∈[0.25,1]范圍內都具有混沌行為，且由STBCS生成的3個混沌映射比由它們對應的種子映射生成的混沌映射具有更大的Lyapunov指數，這表明它們有良好的混沌性和魯棒性。

3.2 復雜性分析

樣本熵來源于近似熵，是對時間序列復雜度的度量，它可以用來描述由動態系統產生序列的相似性[15]。樣本熵越大，其規律程度越低，即動態系統越復雜。由STBCS生成的新混沌LS映射和它的種子映射即Logistic、Sine映射的SE曲線圖如圖7(a)所示，新混沌LT映射和它的種子映射即Logistic、Tent映射的SE曲線圖如圖7(b)所示，新混沌TS映射和它的種子映射即Tent、Sine映射的SE曲線圖如圖7(c)所示。

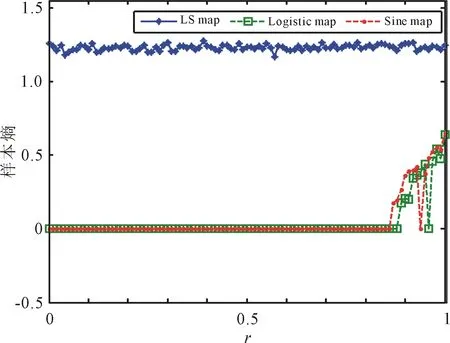
(a) LS映射以及它們種子映射的樣本熵

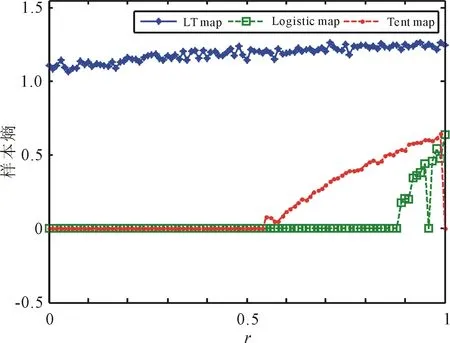
(b) TS映射以及它們種子映射的樣本熵

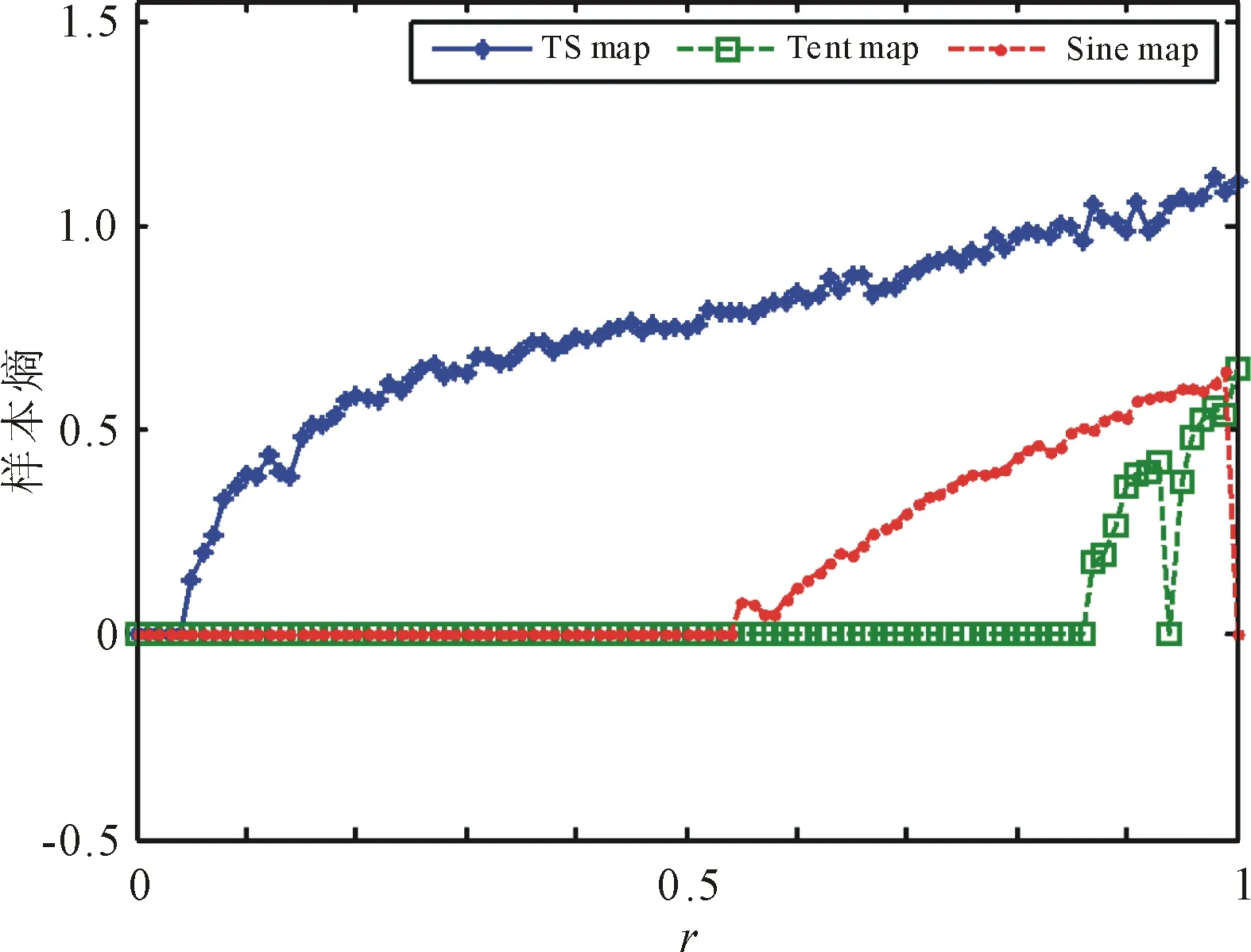
(c) TS映射以及它們種子映射的樣本熵

可以觀察到由所提出的STBCS生成的所有新混沌映射在整個參數范圍內的SE值均大于其種子映射即Logistic映射、Sine映射和Tent映射的SE值。表明STBCS生成的新混沌映射規律程度低，即動態系統更具復雜性。

3.3 不可預測性分析

Kolmogorov熵是一種度量熵，為有限對象的隨機性提供了數學解釋[16]。Kolmogorov熵表示使用其先前t次輸出軌跡需要多少額外信息去預測第(t+1)次輸出。Kolmogorov熵意味著需要額外的信息來預測軌跡，Kolmogorov熵越大表示所需的信息越多。具有正Kolmogorov熵的動力系統被認為是不可預測的，更大的Kolmogorov熵意味著更好的不可預測性。LS、LT、TS映射及其種子映射的Kolmogorov熵，如圖6所示。

(a) LS映射及其種子映射的Kolmogorov熵

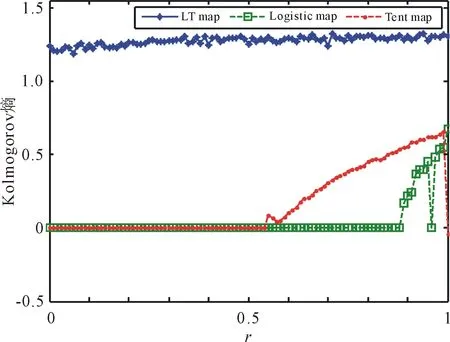
(b) LT映射及其種子映射的Kolmogorov熵

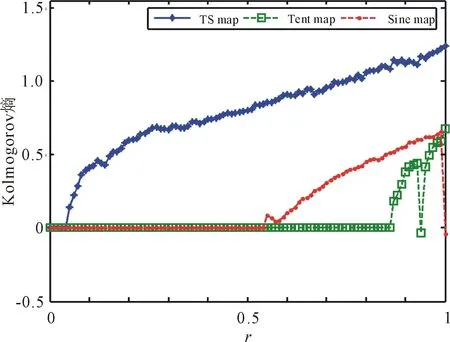
(c) TS映射及其種子映射的Kolmogorov熵

從圖6中可以看出，STBCS生成的新混沌映射，即LS映射、LT映射和TS映射可以在整個參數范圍內獲得正Kolmogorov熵，并且它們的Kolmogorov熵值遠大于它們對應的種子映射的Kolmogorov熵值，這意味著所提出的STBCS可以生成更好的、不可預測的混沌映射，其混沌性能更優。

4 結語

本文提出了一種基于正弦變換的STBCS混沌系統，可作為生成一維混沌映射的一般框架。STBCS混沌系統首先線性加權地組合2個現有混沌映射的輸出，然后對組合結果執行正弦變換得到新的混沌系統。為了證明STBCS生成的新混沌映射的有效性，列舉出了3個用該方法構造的新混沌映射，通過matlab仿真軟件分析了它們的動力學特性。利用分叉圖、Lyapunov指數、樣本熵和Kolmogorov熵進行性能分析和評估。實驗結果表明，基于正弦變換的混沌系統所產生的新的混沌映射在整個區間上出現混沌行為的比例為100%，相較于原有經典的Logistic、Sine、Tent映射出現混沌行為的比例分別提高了89.25%、85%、40%，最大的Lyapunov指數提高了0.5個單位，樣本熵和Kolmogorov熵也均有所提高。STBCS生成的新混沌映射比其相應的種子映射產生的混沌映射具有更大的混沌范圍、魯棒性，更好的復雜性和不可預測性。