刺繡機針桿機構運動精度的靈敏度分析

郭惠昕， 張干清

(長沙學院 機電工程學院， 湖南 長沙 410003)

電腦自動刺繡機的刺布機構(即針桿機構)是一個較為復雜的平面連桿機構。文獻[1]介紹了GY4-1型繡花機的傳動系統及針桿機構的組成和工作原理，并對針桿的運動規律進行了分析，其中特別指出：由于該機構運動環節多、累計誤差上升，導致裝配調試中出現針桿軸向竄動量偏大的問題(實質上就是針桿運動誤差偏大的問題)。針桿機構是形成刺繡線跡的重要機構之一，直接影響繡品的刺繡質量，因此，針桿的運動精度分析是刺繡精度分析研究的重要基礎內容[2]。目前，相關研究思路主要體現在以下幾個方面：1)在不考慮機構制造誤差的情況下，對針桿機構的運動規律進行分析與計算[3-4]；2)計入機構各桿長的制造誤差，對刺繡機的針桿運動精度進行分析和對比[5]；3)在計入機構的各桿長制造誤差及運動副間隙影響的前提下，探討機構各桿長基本尺寸及其制造公差的優化設計問題[6]。綜合現有文獻來看，現有的研究成果基本聚焦在針桿運動誤差的分析與設計計算上，尚未能很好地解決文獻[1]中指出的針桿運動誤差偏大的問題。

要提高針桿機構的刺繡精度，必須提高針桿機構各構件的加工制造精度等級，同時要提高針桿機構的組裝質量[2]。雖然，普遍提高各構件的制造精度肯定能提高針桿的刺繡精度，但是這種方法無疑也會導致機器制造成本的大幅增加。實際上，針桿的運動誤差是機構各桿長的基本尺寸及其制造誤差、各運動副的制造誤差(即運動副的間隙)等眾多影響因素的非線性函數，且各個因素影響針桿運動精度的重要度并不相同。若能找到影響針桿運動精度的重要因素或關鍵因素，就可以在維持非重要因素的制造精度不變的情況下，僅僅針對性地提高這些重要因素的制造精度，從而達到既可有效提高針桿運動精度，有效控制制造成本的目的。

基于上述分析，本文考慮針桿機構各構件的桿長制造誤差以及運動副間隙等因素的影響，運用Sobol′全局靈敏度分析方法[7]對針桿運動精度進行靈敏度分析；根據靈敏度分析結果，對各影響因素的重要度進行排序，找到導致針桿實際運動出現較大誤差的關鍵因素；然后，針對關鍵因素采取針對性的有效措施進行機構設計的優化。本文方法可有效地提高針桿的刺繡精度，對提高刺繡機的設計質量具有實際意義。

1 Sobol′全局靈敏度分析方法簡介

Sobol′方法[7-8]是一種基于模型分解和方差分析的全局靈敏度分析方法，可解決具有隨機變量的系統靈敏度分析問題。設所研究的系統模型為

f=f(x)，x=(x1,x2,…,xn)

(1)

式中：x∈In，I為單位區間[0,1]，In為n維單位超立方體。Sobol′方法的基本思想是把f(x)分解為2n項之和[7]，即：

(2)

式中：1≤i1≤…≤is≤n。則，f(x)的總方差為

(3)

式中：所有積分的積分域均為In。f(x)的偏方差為

(4)

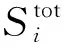
Si=Di/D

(5)

(6)

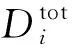
式(3)～(6)中的f0及Di等統計量可采用蒙特卡洛方法進行隨機模擬計算[8-9]。

2 針桿機構運動精度的數學模型

自動刺繡機的針桿機構[1-2]如圖1所示。曲柄①為主動件，由調速電動機驅動繞A點作逆時針轉動；曲柄轉角φ=φ1-φ0，φ0為當曲柄①與連桿②共線時曲柄①與鉛垂線之間的夾角。

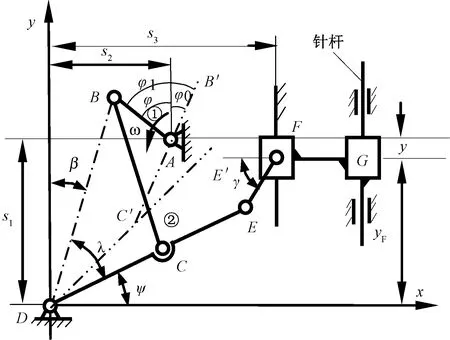
①—曲柄；②—連桿圖1 針桿機構示意圖Fig.1 Schematic diagram of needle bar mechanism

該機構是一個比較復雜的平面連桿機構，其幾何參數有如下幾何關系[1-2]：

(7)

式中lAB為曲柄①的桿長，其他構件長度的表示與此類似。

針桿的位移y可由下式計算：

(8)

其中：

(9)

式(8)中沒有考慮運動副的間隙。現引入有效桿長的概念，計入回轉副間隙的影響，用有效桿長[6,10]替代上述公式中的桿長，則針桿位移可表達為

y=y(φ,x,z)

(10)

式中：x=(x1,x2,…,x14)，z=(z1,z2,…,z6)。隨機變量x為考慮各桿長的制造誤差以及各回轉副間隙引起的偏心距rk后的機構幾何尺寸集合，噪聲因素z為各回轉副偏心距rk的隨機分布方位角δk的集合；k=(a,b,…,f)，各k值分別與圖1中各回轉副的大寫字母編號對應。x和z的所有元素均為隨機變量。

GY4-1型電腦自動刺繡機的原型機為日本田島的TMEF912刺繡機，文獻[3]給出了該原型機37個特定曲柄轉角φi值對應的針桿位移實測值y0i，(i=1,2,…,37)。為了檢驗GY4-1是否達到原型機的性能，取

(11)

式中：yi為GY4-1型電腦自動刺透機在37個特定曲柄轉角φi值對應的針桿位移；yi用式(10)進行計算。

顯見，F的值越小，則針桿的運動精度越高，因此，式(11)可作為表征針桿機構運動精度的數學模型。

3 針桿機構運動精度的靈敏度分析

3.1 針桿機構運動精度的影響因素

針桿運動精度的靈敏度分析需要找到導致針桿實際運動出現較大誤差的關鍵因素。現以針桿機構的一種已知設計方案[6]為例進行靈敏度分析探討。

以式(11)作為靈敏度分析數學模型，其中，運動精度影響因素x和z的各元素及其分布規律列于表1。表中有關變量的均值[6]分別為：μ1=47.5，μ2=15.3，μ3=54.0，μ4=10.1，μ5=52.5，μ6=27.6，μ7=55.3，μ8=18.4。

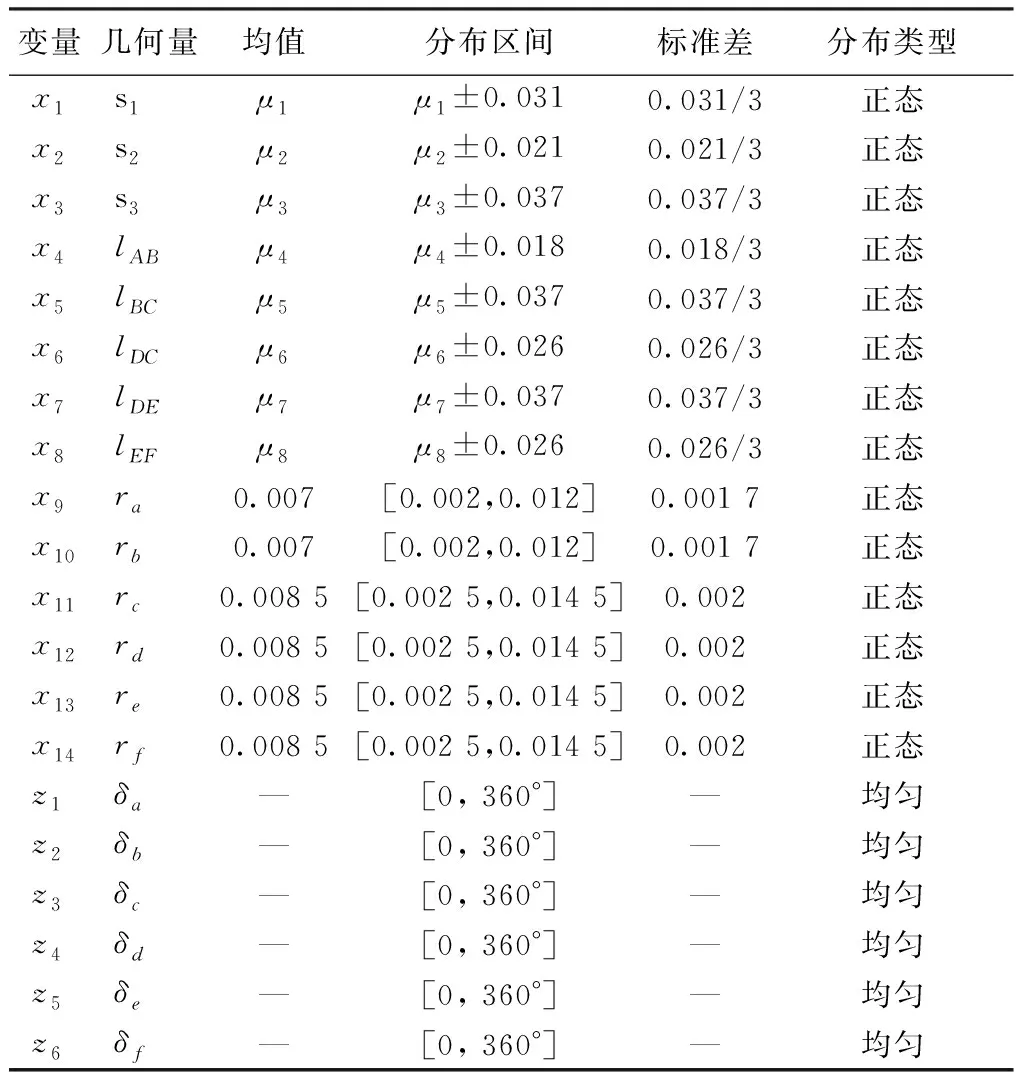
表1 針桿運動精度的影響因素及其分布規律Tab.1 Influence factors and distribution rules of needle bar motion precision

值得說明的是，z對針桿位移的精度有影響，但z為設計制造過程中的不可控因素，因此，僅需分析x的14個元素對針桿位移精度的靈敏度。

3.2 靈敏度分析及結論

在MatLab平臺上編寫基于Sobol′方法的靈敏度分析蒙特卡洛模擬程序。為保證隨機模擬過程中的抽樣均勻，抽樣方法可采用抽樣均勻性較好的拉丁超立方抽樣方法[11]或Sobol′隨機序列法[12]，本文編程采用后者。

根據靈敏度分析結果，按x各元素的總靈敏度指標值大小進行排序，結果如圖2所示。

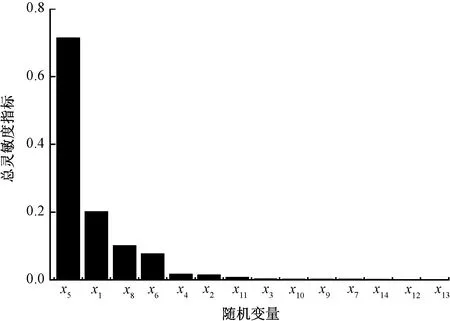
圖2 優化前總靈敏度的條形圖Fig.2 Bar chart of total sensitivities before optimization

由圖2可得如下結論：總靈敏度指標值較大的有4個因素，其總靈敏度值Stot依次是Stot(x5)=0.713 915，Stot(x1)=0.201 118，Stot(x8)=0.101 174，Stot(x6)=0.077 467。靈敏度值越大，說明該影響因素對針桿運動精度的影響越明顯，因此，這4個因素就是影響針桿機構刺繡精度的重要因素。其中，總靈敏度值最大的x5是關鍵因素。總靈敏度值很小甚至接近于零的那些因素，屬于非重要因素，它們對針桿機構運動精度的影響也就很小。

4 基于靈敏度分析的針桿機構優化

靈敏度分析的目的是要找到影響針桿機構運動精度的重要因素，并指導設計者針對性地采取措施，以便進一步優化機構的設計質量。為此，在上節所述針桿機構的設計方案[6](稱為優化前方案)基礎上，進行機構的進一步優化設計。

4.1 優化思路與優化方案

由圖2可知，x5為影響針桿運動精度的關鍵因素，代表圖1中的連桿②的長度及其制造誤差。表1中所示lBC的偏差是±0.037，精度等級是IT9。現維持x5的均值不變，即仍取μ5=52.5，但將其制造精度等級提高1級，其尺寸偏差變為±0.023。其他所有尺寸及其精度等級仍保持表1中的參數不變，即和優化前方案一樣。

4.2 優化效果分析對比

對上述優化方案再進行一次靈敏度分析，分析結果及其靈敏度排序見圖3。

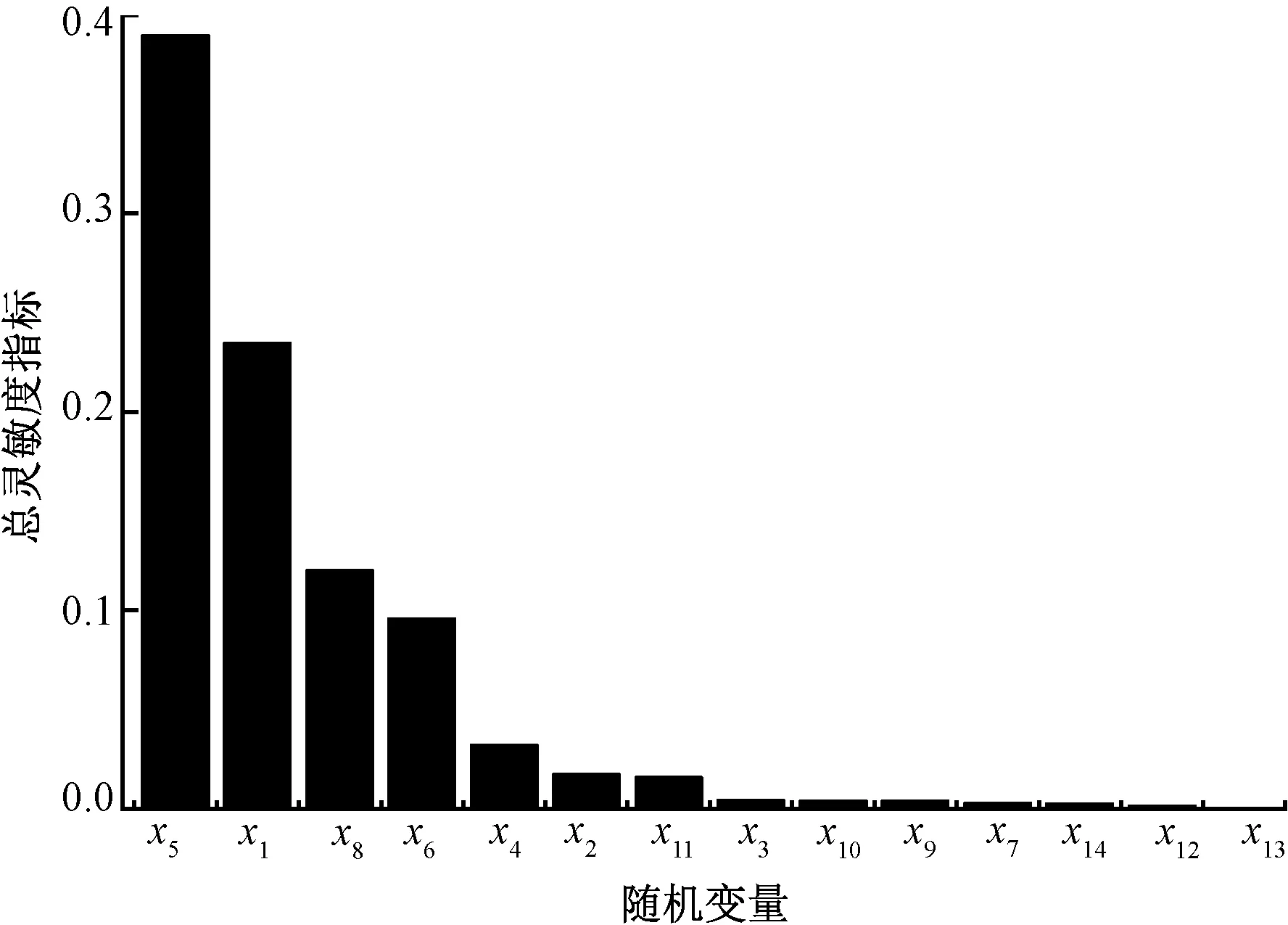
圖3 優化后總靈敏度的條形圖Fig.3 Bar chart of total sensitivities after optimization

此時，4個重要因素的總靈敏度值發生了變化，它們依次是：Stot(x5)=0.389 891，Stot(x1)=0.234 580，Stot(x8)=0.120 147，Stot(x6)=0.095 805。x5仍為影響針桿運動精度的關鍵因素，但其總靈敏度值已經大幅減小。

經過上述的進一步優化后，針桿機構的運動精度應該有所提高。為檢驗優化效果，針對第2節中提到的37個特定曲柄轉角φi值，對針桿位移精度進行隨機模擬計算，優化前后2種方案的模擬結果如圖4、5所示。

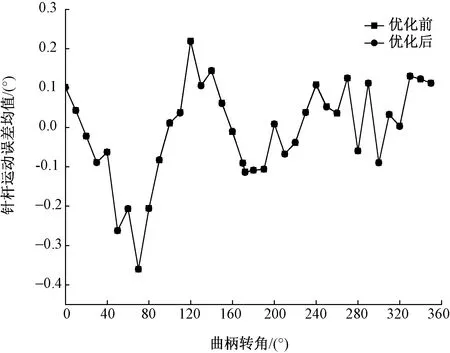
圖4 優化前后針桿運動誤差的均值Fig.4 Mean values of needle bar motion error before and after optimization

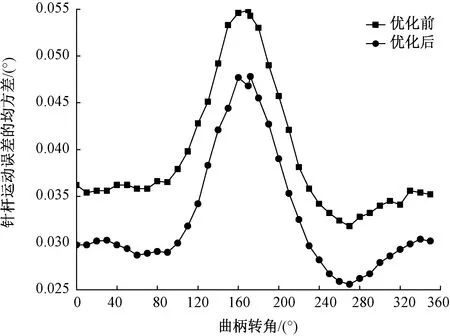
圖5 優化前后針桿運動誤差的均方差Fig.5 Mean square deviation of needle bar motion error before and after optimization

由于沒有改變x(5)(即lBC)的均值，故進一步優化后針桿位移誤差的均值和優化前基本相同，圖4中2條曲線基本重合，但是，優化后針桿位移誤差的均方差明顯減小(見圖5)。文獻[1]指出了GY4-1型繡花機在裝配調試中出現的針桿軸向竄動量偏大的問題，而影響竄動量大小的主要因素是針桿位移誤差的離散性。針桿運動誤差的均方差越小，其位移誤差的離散性越小，因此，經過進一步優化后，針桿軸向竄動量將減小，針桿位移精度的穩健性得到進一步提高。

5 結 論

1) 靈敏度分析是研究與分析一個模型 (或系統)的輸出(或響應)的變化對系統參數的敏感程度的方法。通過靈敏度分析可以確定出哪些參數對模型輸出有較大的影響，并可確定出影響模型輸出變異的重要因素。研究針桿機構運動精度的靈敏度問題，可找到影響其運動精度的關鍵因素，以便對現有設計方案進行評價，并為進一步優化提供依據，具有重要的工程意義。

2) 采用Sobol′方法對文獻[6]中針桿機構優化設計方案進行了全局靈敏度分析，求解出影響針桿運動精度的所有14個變量的總靈敏度，找出14個變量中的4個重要因素及1個關鍵因素。其中，連桿長度是關鍵因素。

3) 在靈敏度分析的基礎上，采取針對性的有效措施，通過減少關鍵因素連桿長度的制造誤差，對原設計方案進行了進一步優化。通過隨機模擬得到了37個特定曲柄轉角處的針桿位移誤差的均值和均方差。對比可見，進一步優化后，針桿位移誤差的均方差明顯減小，有效地提高了機構運動精度及其穩健性，優化了針桿機構的設計質量。

FZXB