基于全相位譜分析的多頻內插迭代頻率估計器

黃翔東， 黎鳴詩， 羅 蓬， 馬 欣

(1. 天津大學 電氣自動化與信息工程學院，天津 300072； 2. 國網河北省電力公司電力科學研究院， 石家莊 050021)

頻率估計的應用非常廣泛(如多普勒效應檢測[1]，振動學中的轉速測量[2]都可轉化為頻率估計問題)。相比于基于子空間分解(如多重信號分類法[3]、旋轉不變參數估計法[4]等)的頻率估計算法，FFT(Fast Fourier Transform)因其具有運算效率高的優勢，因而基于FFT的頻率估計器一直是學術研究的熱點問題。?

Stoica等[5]指出：給定有限長樣本，最大似然意義上的頻率估計值位于該序列的DTFT(Discrete Time Fourier Transform)的峰值位置，但是DTFT的理想譜峰需要對頻率做高分辨率掃描才可搜索得到, 顯然頻率掃描會增加估計器的計算復雜度。為降低復雜度, 通常的做法是對序列做FFT(而不是DTFT)，進一步對FFT峰值譜附近的譜線采取內插、迭代等措施，對FFT譜峰附近的譜值做進一步修正和細化來提升頻率估計精度。從而不同的內插算法就可以產生不同的頻率估計器(如Quinn估計器[6]、能量重心估計器[7]、Macleod估計器[8]、Jacobsen估計器[9]、Candan估計器[10]、相位差估計器[11-14]、比值估計器[15]、AM譜估計器[16]、細化譜估計器[17]、Tsui估計器[18]等)。

需指出，對于單頻信號的FFT頻率估計器，經過不斷完善，其精度幾乎不存在提升的空間(如文獻[16]提出的AM估計器的頻率估計方差僅為克拉美-羅限的1.014 7倍，而文獻[18]提出的Tsui估計器的估計方差幾乎逼近克拉美-羅限[19](Cramer-Rao lower Bound，CRB)。但是當對多頻信號做FFT譜分析時，由于FFT固有的譜泄漏，各頻率成分之間會嚴重的譜間干擾，導致Quinn等的估計器精度都會大幅度降低。

因而，提升多頻信號的頻率估計精度的關鍵在于：選擇比FFT更優良的抑制譜泄漏性能的譜分析方法，基于此設計出具體的內插措施。王兆華等[20-21]指出，全相位FFT(all-phase FFT，apFFT)相比于傳統FFT，具有更優良的抑制譜泄漏性能，黃翔東等[22]還把離散的全相位FFT譜分析延伸到連續的全相位DTFT譜分析(all-phase DTFT, apDTFT)領域，從而拓寬了其理論內涵。故本文用全相位FFT替代傳統FFT譜分析，通過分析信號頻偏值與譜峰附近apDTFT譜的內在聯系，設計出一種迭代多頻內插估計器。仿真實驗表明：給定同樣數目的觀測樣本，本文估計器比Tsui估計器具有更高的估計精度。由于工程應用中的多頻信號比單頻信號更為廣泛，故本文估計器具有較高的應用價值。

1 全相位FFT和全相位DTFT基本原理

1.1 全相位FFT譜分析

王兆華等[23]提出的apFFT譜分析簡化流程，如圖1所示。

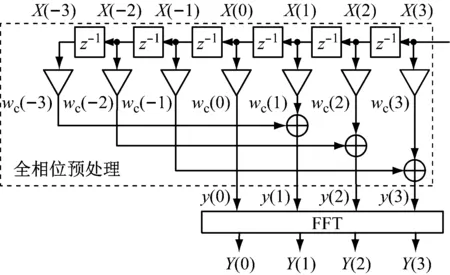
圖1 apFFT譜分析簡化流程(N=4)

圖1的apFFT譜分析分為兩個簡單步驟：

步驟1全相位數據處理，用長為2N-1的卷積窗wc(n)對輸入數據x(n)加權，然后將間隔為N的數據兩兩疊加而得到y(0),y(1),…,y(N-1)；

步驟2對y(0),y(1),…,y(N-1)做FFT即得全相位離散譜Y(k)。

圖1中的卷積窗wc(n)是由長為N的窗f(n)和翻轉的窗b(n)通過卷積得到，即

wc(n)=f(n)*b(-n),n∈[-N+1,N-1]

(1)

本文取f(n)=b(n)=RN(n)，其中RN是長為N的矩形窗。

令Δω=2π/N，ω0=(k*+δ)Δω,其中k*∈Z+,δ∈[-0.5,0.5)。黃翔東等[22]已證明，對于單頻復指數信號

x(n)=A·ej(ω0n+θ0),n∈[-N+1,N-1]

(2)

其歸一化的apFFT譜值為

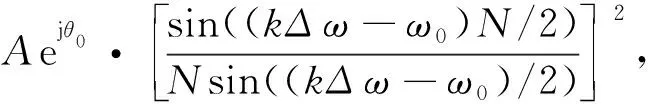
k=0…,N-1

(3)

式(3)的平方項使得旁譜線Y(k),k≠k*,相對于峰值譜Y(k*)出現大幅度衰減，使得峰值譜更突出，因而apFFT具有比傳統FFT更優良的抑制譜泄漏性能。

1.2 全相位DTFT譜分析

黃翔東等提出的apDTFT的簡化流程，如圖2所示。

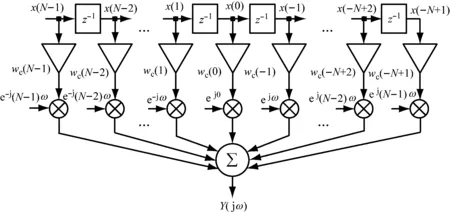
圖2 apDTFT譜分析的簡化流程

圖2的apDTFT輸出為

(4)

式中:ω為頻率掃描變量。因而不同于離散的apFFT譜，apDTFT譜Y(jω)為連續譜。

黃翔東等已證明，對于式(2)中的單頻復指數信號，其apDTFT譜的理論值Y(jω)為

(5)

聯立式(3)，式(5)，有

Y(k)=Y(jω)|ω=kΔω,k=0,…,N-1

(6)

因而apFFT譜Y(k)可看作是在ω∈[0,2π)內對apDTFT譜Y(jω)的等間隔離散采樣結果。兩者都是全相位譜分析理論的重要組成部分。

特別地，易證明在距離譜峰的兩個對稱頻點ωL=ω0-0.5Δω、ωR=ω0+0.5Δω處的apDTFT值同為

(7)

2 全相位譜分析的迭代多頻內插估計器設計

2.1 apDTFT峰值譜附近的頻偏估計機理

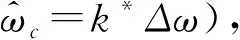
ωL=kLΔω=(kc-0.5)Δω

(8)

ωR=kRΔω=(kc+0.5)Δω

(9)

把式(8)和式(9)代入式(5)，可推導出這兩個頻點處的apDTFT譜幅值分別為

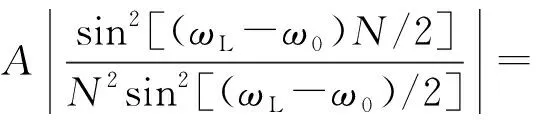
(10)

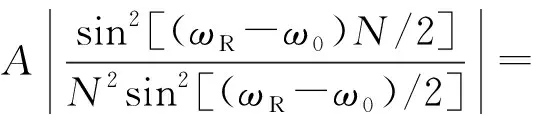
(11)

聯立式(10)和式(11)可得左譜線與右譜線幅值之比為

(12)

因為δ∈[-0.5,0.5)，則式(12)等號右邊去掉絕對值符號后可表示為

(13)

當N足夠大，根據無窮小關系：sin[(δ-0.5)π/N] ～(δ-0.5)π/N，sin[(δ+0.5)π/N]～(δ+0.5)π/N，則式(13)可近似表示為

由表5可知，安徽省區域旅游發展水平差異明顯．黃山市與池州市旅游區位熵得分較高，旅游產業發展水平在省內處于領先地位．黃山市、池州市、安慶市、宣城市、合肥市、蕪湖市、六安市旅游區位熵均大于0.74，旅游業發展狀況較好，可劃分為旅游發展的優勢區域;其他城市均小于0.74，旅游業發展狀況一般，可劃分為一般旅游區域．

(14)

利用上式可解得頻偏估計值

(15)

2.2 迭代估計過程

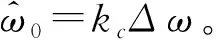
從圖3可看出，只在初始化階段做了1次apFFT譜分析，而且迭代過程中也只涉及兩個特殊頻點ωL、ωR的apDTFT值的更新，從而繞開了apDTFT連續譜的頻率掃描過程，故圖3流程復雜度低。

2.3 迭代趨勢分析

搜索出apFFT峰值譜位置后，在第1次迭代中，兩個頻點ωL、ωR上的apDTFT譜不外乎兩種情況：|Y(jωL)|≤|Y(jωR)|和|Y(jωR)|<|Y(jωL)|，其分布分別如圖4(a)、4(b)所示。

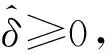
圖3 單頻迭代估計流程圖

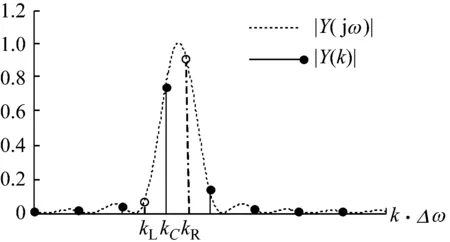
(a) |Y(jωL)|<|Y(jωR)|

(b) |Y(jωL)|>|Y(jωR)|

理想情況下，由式可推知|Y(jωL)|=|Y(jωR)|成立。故對于圖3迭代流程，可采用兩者差異的比例作為迭代終止條件。經驗表明，將閾值取為ε∈(0.004，0.3)，只需2次迭代即可獲得高精度頻率估計。

2.4 多頻成分的頻率估計

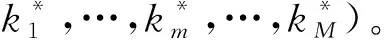
需指出，與單頻成分不同的是，多頻成分的頻率估計誤差來源除了外加噪聲和估計器本身的系統誤差(如式(14)中等價無窮小引入的誤差)外，各成分的譜間干擾也是誤差源的主要方面。由于apFFT譜分析具有比傳統FFT譜分析更優良的抑制譜泄漏性能，故譜間干擾更小，因而其多頻估計器精度高于文獻[6-18]中的估計器。以上結論將通過第3節中的實驗來證明。

2.5 多頻信號重構

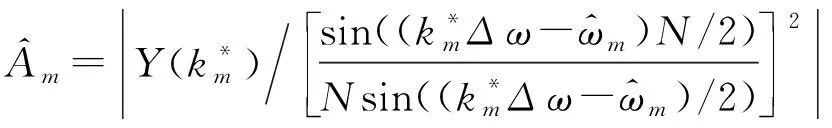
(16)

(17)

式中,ang(·)表示取相角操作。

從而，包含多個頻率成分的實信號的重構式為

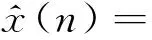
n∈[-N+1,N-1]

(18)

3 實 驗

例1令N=64,M=3,ω1=7.1Δω,ω2=9.35Δω,ω3=12.2Δω,對信號x(n)=ejω1n+3ejω2n+ejω3n,n=-N+1,…,N-1，分別進行64階apFFT、apDTFT及其127點的FFT和DTFT，其譜圖分別如圖5(a)、5(b)所示。并且分別用本文的頻率估計器和文獻[18]的Tsui估計器(選該估計器的原因是：其誤差方差逼近CRB，幾乎是精度最高的FFT估計器)分別進行頻率估計，表1給出兩個估計器的相對誤差，其算式為

(19)

從圖5明顯可看出，apFFT、apDTFT的譜泄漏遠小于FFT、DTFT的譜泄漏(即除3個主峰外，前者的帶外起伏比后者小得多)，這意味著對于3個成分間的譜干擾，前者也比后者小得多。從表1數據也可看出，本文估計器的相對誤差也遠小于Tsui估計器情況。

(a) apFFT、apDTFT譜圖

(b) FFT、DTFT譜圖

η1/%η2/%η3/%本文估計器0.120.010.06Tsui估計器0.330.030.36

例2調研含噪情況下，不同頻率間距的各成分的譜間干擾對頻率估計器的影響。不妨令N=64,M=2,輸入信號為x(n)=ejω1n+ejω2n+ξ(n)，其中ξ(n)為加性高斯復噪聲。固定ω1=5.25Δω，ω2分別取值為9.15Δω，8.15Δω，7.15Δω，6.15Δω。圖6～圖9給出不同信噪比(Signal to Noise Ratio, SNR)條件下，本文估計器、Tsui估計器的均方根誤差以及CRB的平方根曲線。

從圖6～圖9的RMSE曲線，可得出如下結論：

(1) 在低信噪比區域(SNR<10 dB)，本文估計器的SNR閾值普遍比Tsui估計器低，這意味著其抗噪魯棒性強于Tsui估計器。這是因為對于Tsui估計器，多頻信號較大的譜間干擾削弱了抵御強噪聲的能力。

(2) 在中、高信噪比區域(SNR>10 dB)，對于Tsui估計器，其RMSE呈現出平坦的形狀，與CRB曲線偏離非常遠，而本文估計器僅在兩頻率成分間距較小時(即圖8、圖9的情況)，才會與CRB曲線產生較大的偏離。這說明，在中、高信噪比情況，影響估計器精度的主導因素，既不是外加噪聲，也不是系統誤差，而是各成分間的干擾，而全相位譜分析的譜間干擾遠小于傳統譜分析情況，故其RMSE曲線更貼近于理論下限。

(3) 當頻率間距過小時(低于1Δω，即對應圖9的情況)，兩個估計器的RMSE都變得很大，這是因為無論全相位譜，還是傳統FFT譜，其各成分譜的主瓣都相互重疊了，故頻率估計失效。

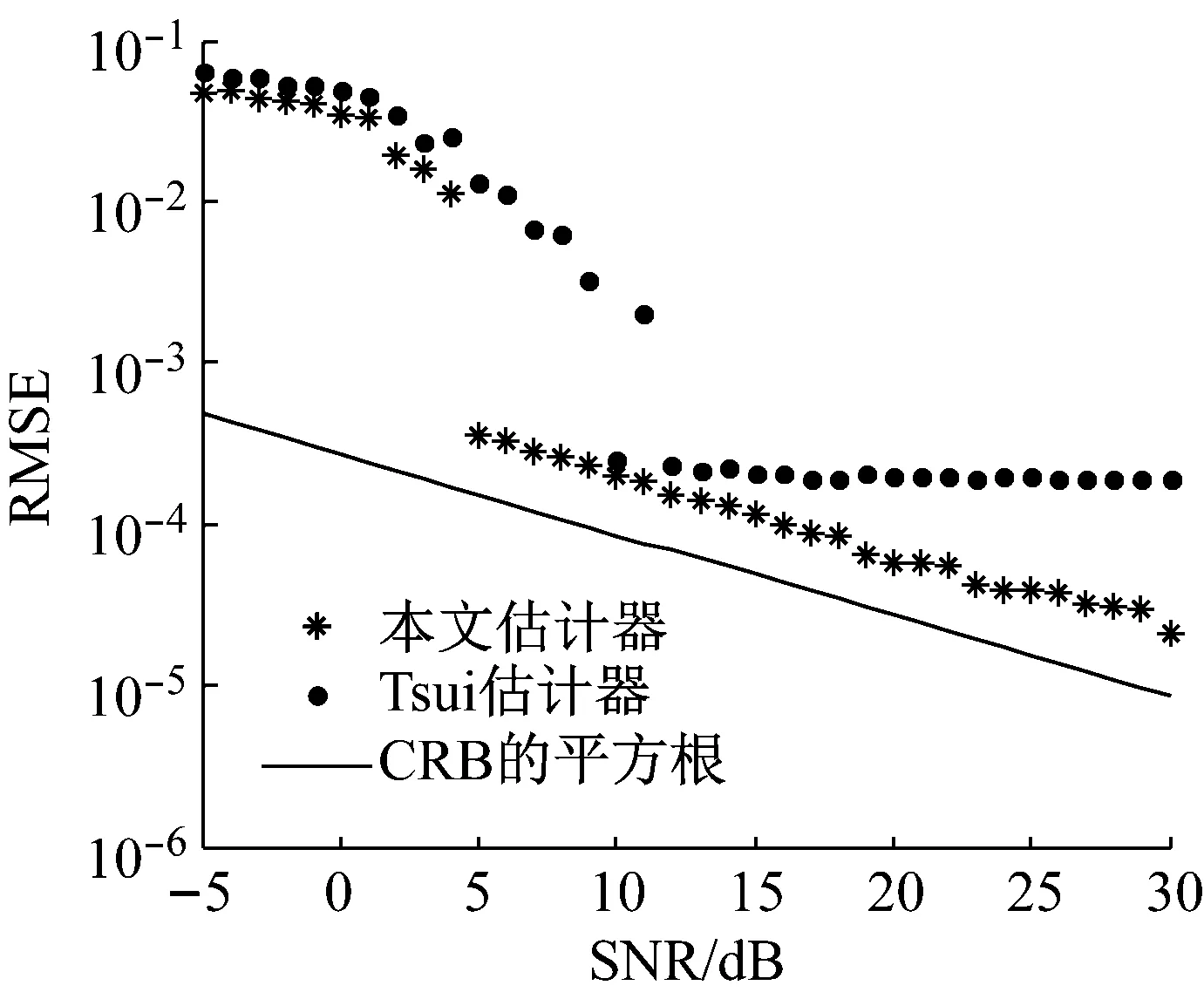
(a) ω1=5.25Δω

(b) ω2=9.15Δω

(a) ω1=5.25Δω

(b) ω2=8.15Δω

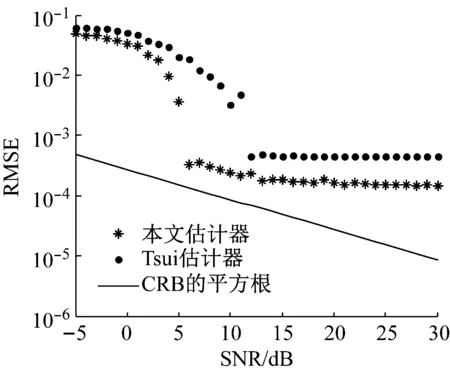
(a) ω1=5.25Δω

(b) ω2=7.15Δω

(a) ω1=5.25Δω

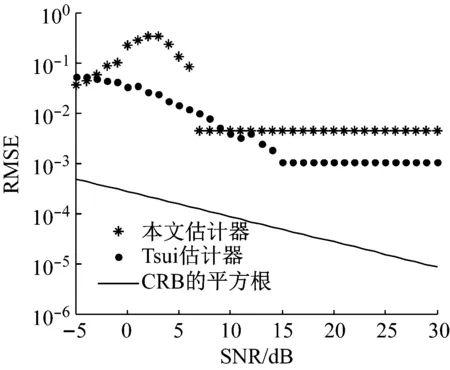
(b) ω2=6.15Δω

γ=10lg(Px/Pe)

(20)

式中，Px為原信號x(n)的平均功率，Pe為e(n)的平均功率。表2給出了兩種估計器的重構。

表2 機械故障信號的兩種估計器重構信噪比

以測量面缺陷信號為例，圖10(a)、(b)分別給出了用全相位FFT的振幅譜|Y(k)|、傳統FFT的振幅譜|X(k)|，圖10(c)給出了原始波形、全相位重構波形和Tsui重構波形。

(a) apFFT振幅譜

(b) FFT振幅譜

(c) 原始波形與兩種重構波形

可明顯看出，圖10(a)的振幅譜|Y(k)|的譜間干擾程度比圖10(b)的振幅譜|X(k)|的譜小很多，這保證了前者的各成分的頻率、幅值、相位參數估計精度高于后者，從而獲得更高的重構信噪比(如表2所示，前者比后者高出2.7 dB)。該結論對于其他兩種故障信號的重構也成立。

4 結 論

本文提出基于全相位譜分析的多頻內插迭代頻率估計器，利用全相位譜分析方法有效地抑制譜泄漏，降低多頻成分間的干擾；再結合內插迭代提高多頻信號的頻率估計精度。由于本文方法在有外界干擾的低信噪比環境仍能高精度地做頻率估計，且仿真實驗和實際信號重構實驗均驗證了本文方法具有更高的參數估計精度，故在多頻信號估計領域有望得到更廣泛的應用。