基于塊稀疏貝葉斯學習的多目標動態熒光分子重建
臧青楊,陳春曉,楊俊豪,李東升
(南京航空航天大學生物醫學工程系,南京 211106)
1 引 言
動態熒光分子成像(dynamic fluorescence molecular imaging, D-FMI)是利用熒光分子探針在體內不同器官中的分布隨時間變化的動態性差異進行成像的技術[1-2]。D-FMI在藥代動力學、腫瘤診斷和病理信息監測等領域有重要的應用前景。動態熒光分子重建是一個嚴重的欠定性問題,壓縮感知理論是有效解決重建欠定性的理論方法之一[3]。基于壓縮感知的范數優化算法是熒光分子逆向重建的常用算法,該算法通過范數正則化項表征待求解模型稀疏度。然而,采用范數優化算法解決在體熒光目標的稀疏重建時,由于采集到的動態熒光信號幀之間相互獨立、重構信號維度高及沒有充分考慮數據在時空域中的相關性與塊稀疏特性,導致重建稀疏度不足、定位精度低等問題[4]。
相較于傳統的壓縮感知算法,基于概率統計的貝葉斯學習(sparse bayesian learning, SBL)具有重建信號稀疏性好、定位精度高等優勢[5]。多目標動態熒光分子重建屬于多觀測向量(multiple measurement vectors, MMV)模型聯合稀疏重建問題。由于動態熒光信號共享相同稀疏結構,塊稀疏模型能利用信號的分塊稀疏特性有效挖掘多觀測信號時空相關性信息[6],因此,本研究采用基于MMV模型的塊稀疏貝葉斯學習(block sparse bayesian learning, BSBL)解決多目標動態熒光分子的重建問題。
2 方法
2.1 動態熒光光子傳輸模型
在熒光分子斷層成像中,通常使用擴散近似方程作為描述光子在生物體組織中傳輸過程的數學模型[7]:
(1)
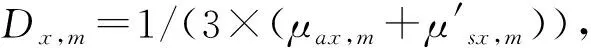
在生物組織邊界應用Robin邊界條件,并結合有限元法求解式(1),可以建立體表光通量密度Φm與光源能量密度S之間的關系:
Φm=AS+v
(2)
其中,S為n維列向量,n是有限元離散后的網格節點個數;Φm為m維列向量,m是體表節點個數;A為m×n的系數矩陣,主要取決于生物體的結構分布和光學特性;v為未知噪聲向量。
動態熒光分子成像技術是在靜態成像的基礎上加入了時間維度,通過采集相繼離散時間點下的熒光信號,根據式(2)建立動態熒光光子傳輸模型:
Φm(t)=AS(t)+v(t),t∈[L]
(3)
其中,Φm(t)為不同觀測時間下的體表光通量密度;S(t)為不同觀測時間下的光源能量密度;L為動態熒光信號的采樣次數,[L]表示1到L的整數集;v(t)為不同觀測時間下引入的未知噪聲。
2.2 BSBL算法
經典的SBL算法是假設待求解向量S的各個元素相互獨立,通過給S的各個元素的權值系數賦予先驗條件概率分布加以限制,并引入相關向量機(relevance vector machines, RVM)稀疏模型,在優化迭代過程中剔除權值系數趨于零的訓練樣本,從而獲取模型的稀疏解[8-9]。
BSBL算法最初在2013年由Zhang等提出,它是一種以分解稀疏向量中每個塊內的元素之間的幅值相關性作為結構先驗信息的新型塊稀疏重構算法[10-11]。BSBL算法首次揭示了塊內相關對塊稀疏信號重構性能的影響,文獻[12]證明了在無噪情況下BSBL求得的全局解即為真正的最稀疏解。
BSBL算法中假定待求解稀疏向量S可以劃分為g個非重疊塊結構,并且S的非零元素集中分布于少數非零塊中,即:
S=[S1,…,Sd1,…,Sdg-1+1,…,Sdg]T
(4)
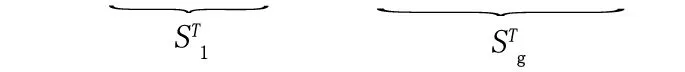
式(2)和式(4)組成了塊稀疏壓縮感知模型,在BSBL算法中,各個信號塊可以具備不同的大小。與之對應,系數矩陣A可分為g個塊矩陣:
A=[A1,…,Ag]
(5)
BSBL算法假設第i個信號塊Si服從多元高斯分布:
p(Si|γi,Bi)=N(Si;0,γiBi)
(6)
其中,γi為一個非負尺度參數,用于控制信號塊Si的稀疏度。當γi=0時,對應信號塊Si則為0。在學習過程中,受自動相關性確定機制影響,大部分γi將趨于0,通過設定合適的閾值將趨于0的γi置為0,從而促成了解的塊稀疏;Bi為一個未知的正定矩陣,表征著該塊內的元素之間的相關結構模型信息。
在假設信號塊與塊之間相互獨立的前提下,待求解向量S的先驗分布可以建模為:
p(S|{γi,Bi})=N(S;0,Γ)
(7)
其中,Γ=diag-1(γ1B1,…,γgBg)。
同時假設觀測噪聲v服從p(v;λ)=N(0,λI)分布。根據貝葉斯準則可得出S的后驗分布為:
p(S|Φm,{γi,Bi},λ)=N(S;μ,∑)
(8)
其中,∑-1=Γ-1+ATλ-1A,μ=∑ATλ-1Φm。
+ΦmT(λI+AΓAT)-1Φm
(9)
采用快速邊緣似然最大化(fast marginal likelihood maximization, FMLM)優化算法對式進行求解,得到所有參量的學習規則為:
(10)
(11)
(12)
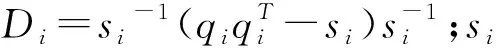
2.3 基于BSBL的多目標動態熒光分子重建
現有的BSBL算法多針對于單觀測向量(single measurement vector, SMV)模型,但在實際應用中常需從MMV模型中重構稀疏信號,本研究的多目標動態熒光分子重建即屬于MMV模型聯合稀疏重構問題。研究表明,相比于SMV模型,MMV模型更能準確估計出稀疏解向量非零行的位置,重構性能更優[13-14]。
MMV模型聯合稀疏重構問題需假定重構源信號是K稀疏的,而且不同源信號之間共享相同的稀疏結構[15]。MMV稀疏重構模型見圖1,源信號s(t)的每一個列向量都是塊稀疏的,同時不同列向量之間共享相同的稀疏結構且具備時域相關性,因此信號塊si的劃分可以利用到信號的時空相關性和塊稀疏特性。
在假設信號塊與塊之間相互獨立的前提下,信號塊Si符合矩陣正態分布,則動態熒光信號S(t)的先驗分布可以建模為:

圖1 MMV稀疏重構模型Fig 1 MMV sparse reconstruction model p(S(t)|{Γ,B})=MN(S(t);0,Γ,B)
(13)
其中,Γ=diag-1(Di),Di為正定對稱矩陣,用來描述稀疏信號塊Si的相關結構信息。
同時假設S(t)的所有列向量滿足同一相關模型B,在式(3)模型下,根據貝葉斯準則對觀測信號Φm(t)進行建模可得:
p(Φm(t)|λ,B)
=MN(Φm(t);AS(t),λIM,B)
(14)
為了估計參量Di與B,采用第二類最大似然估計方法得到代價函數L:
(15)
其中,CA=λIM+AΓAT。
采用優化算法對上式代價函數進行求解,可得待估計參量的學習規則為:
(16)
(17)
3 實驗結果
3.1 數值仿真實驗
本研究數值仿真實驗設置見圖2。圖2(a)為數值仿真幾何模型,大圓柱體作為生物組織,半徑為1.5 cm,高度為3 cm,內置三個小圓柱體作為多目標熒光光源,小圓柱半徑為0.2 cm,高度為0.4 cm,中心坐標分別為(-0.7,0,1.5)、(0.5,0.5,1.5)和(0.5,-0.5,1.5),多目標熒光光源的動態濃度設置見圖2(b)。
為獲取體表測量數據,將幾何模型進行有限元四面體網格剖分,通過COMSOL前向仿真獲取體表光通量密度Φm(t)。M-FOCUSS(multiple fOCal underdetermined system solver)算法是基于MMV模型的稀疏信號重構算法,它利用Lp范數模型對待求解列向量進行約束,相較于L0和L1范數優化模型有著更優的信號重構性能和更高的計算效率。使用M-FOCUSS算法和本研究塊稀疏貝葉斯方法進行重建,重建結果見圖3。
從圖3的對比結果可以看出,M-FOCUSS算法雖然可以重建出光源的大致位置與強度,但存在重建精確度和稀疏度不足的問題,本研究方法可以獲取更精確、更稀疏的重建結果。
通過非負矩陣分解(non-negative matrix factorization, NMF)算法對多目標動態熒光分子重建結果進行分離,獲取多目標光源的動態濃度分布歸一化曲線,見圖4。從圖3和圖4可以看出BSBL算法對動態熒光濃度的重構稀疏度更好、精度更高。
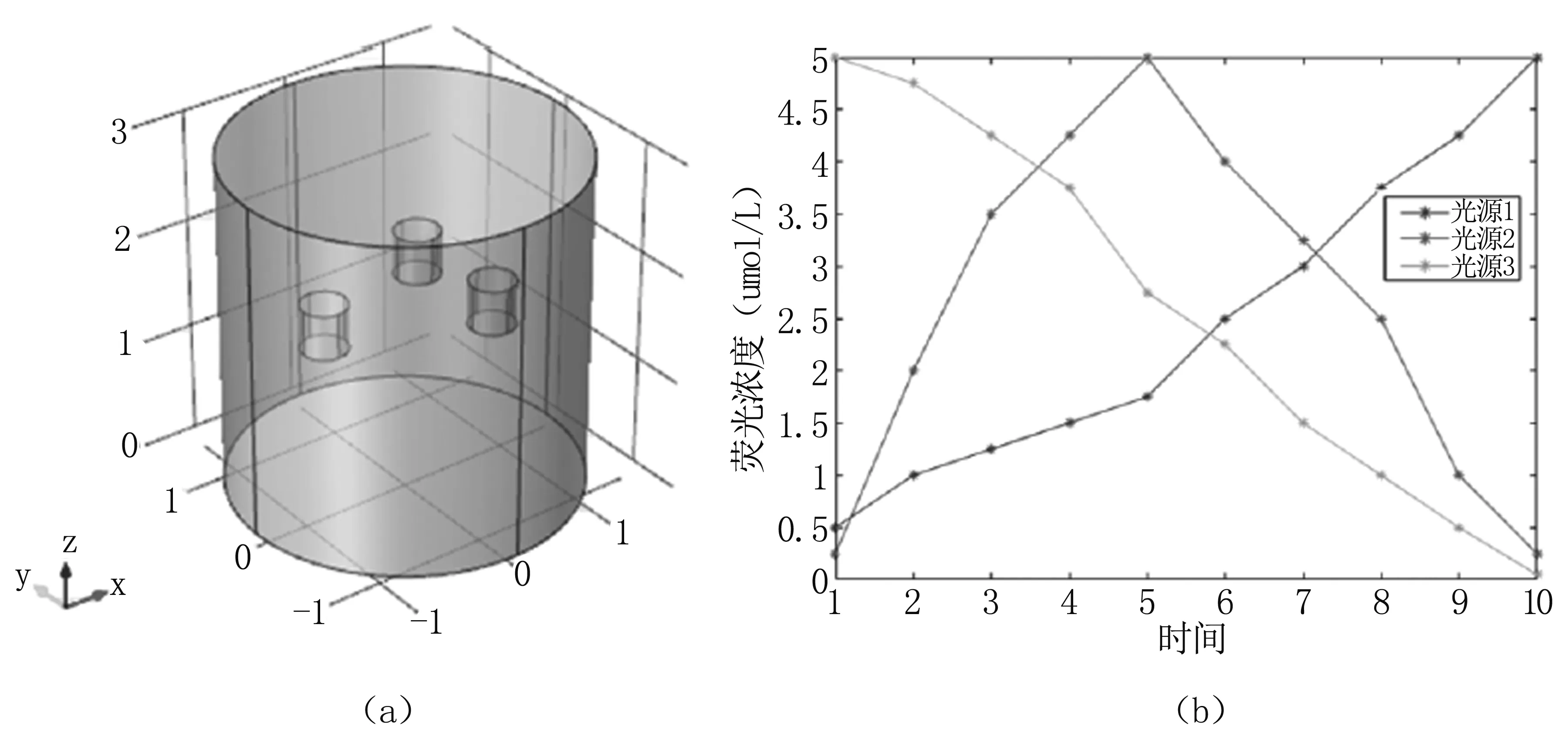
圖2數值仿真實驗設置
(a).仿真幾何模型;(b).動態熒光濃度設置
Fig2Numericalsimulationexperimentsetup
(a).geometricmodel;(b).dynamicfluorescenceconcentrationsettings

圖3 t=4時,數值仿真重建結果(a)、(b).真實光源位置和濃度;(c)、(d).M-FOCUSS算法重建結果;(e)、(f).塊稀疏貝葉斯重建結果Fig 3 Results of numerical simulation reconstruction, when t=4 (a)、(b).the position and intensity of true light source;(c)、(d).the reconstruction results of M-FOCUSS algorithm;(e)、(f).the reconstruction results of BSBL
3.2 生物組織實驗
本研究設計了在豬肉組織內部植入雙腫瘤源的實驗對重建算法進行驗證,動態腫瘤源由不同濃度的吲哚菁綠(indocyanine green, ICG)溶液密封在透明導管構成。豬肉組織實驗設置見圖5,其中豬肉組織的長為5.5 cm,寬為3 cm,高度為3 cm,內置腫瘤源半徑為0.1 cm,高度為0.2 cm,中心坐標分別為(1.7,1.5,2.1)和(3.8,1.5,2.1),雙腫瘤源動態濃度設置見圖5(b)。
體表光學圖像由課題組搭建的小動物光學成像系統AOIS獲取,采集的二維動態熒光圖像見圖6。
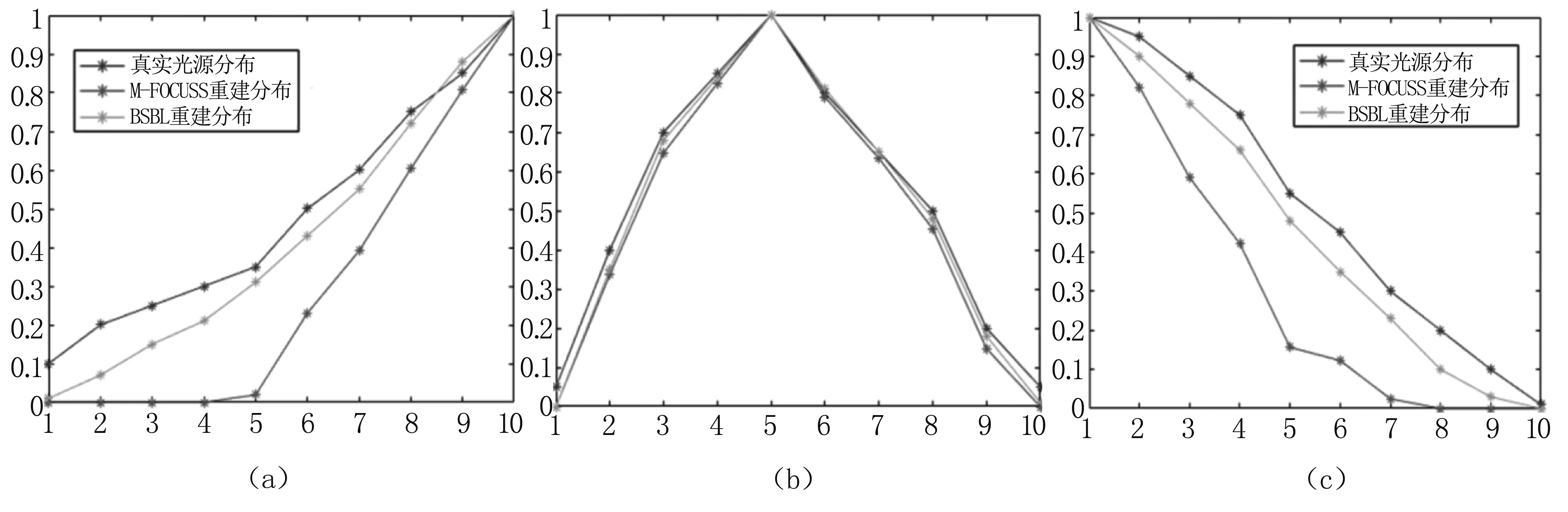
圖4動態熒光分離結果
(a)、(b)、(c)分別為tube1、tube2和tube3的動態熒光濃度歸一化曲線
Fig4Resultsofdynamicfluorescenceseparation
(a),(b),(c),arenormalizedcurvesofdynamicfluorescenceconcentrationfortube1,tube2andtube3respectively
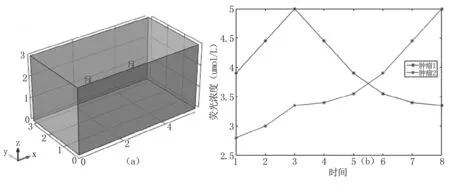
圖5 豬肉組織實驗設置(a).豬肉組織幾何模型;(b).雙腫瘤源動態熒光濃度設置Fig 5 Pork tissue experiment setup(a).pork tissue geometric model;(b).dual tumor dynamic fluorescence concentration setting
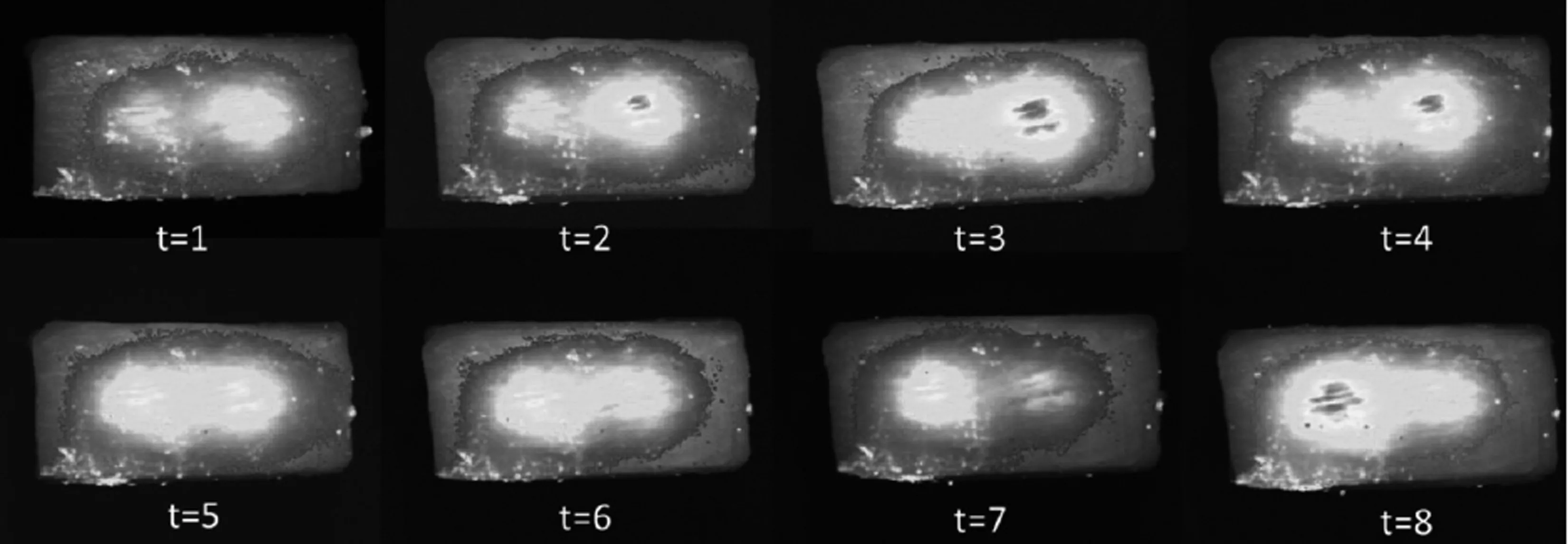
圖6 二維動態熒光圖像Fig 6 Two dimensional dynamic fluorescence image
使用M-FOCUSS算法和本研究方法對豬肉實驗數據進行重建,重建結果見圖7。
對豬肉組織實驗重建結果進行動態濃度分離,獲取動態腫瘤源的動態濃度分布曲線,如圖8所示。

圖7t=4時,豬肉組織實驗重建結果
(a)、(b).真實腫瘤位置和濃度;(c)、(d).M-FOCUSS算法重建結果;(e)、(f).塊稀疏貝葉斯重建結果
Fig7Reconstructionresultsofporktissue,whent=4
(a)and(b)arethepositionandintensityoftruetumour;
(c)and(d)arethereconstructionresultsofM-FOCUSSalgorithm;(e)and(f)arethereconstructionresultsofBSBL
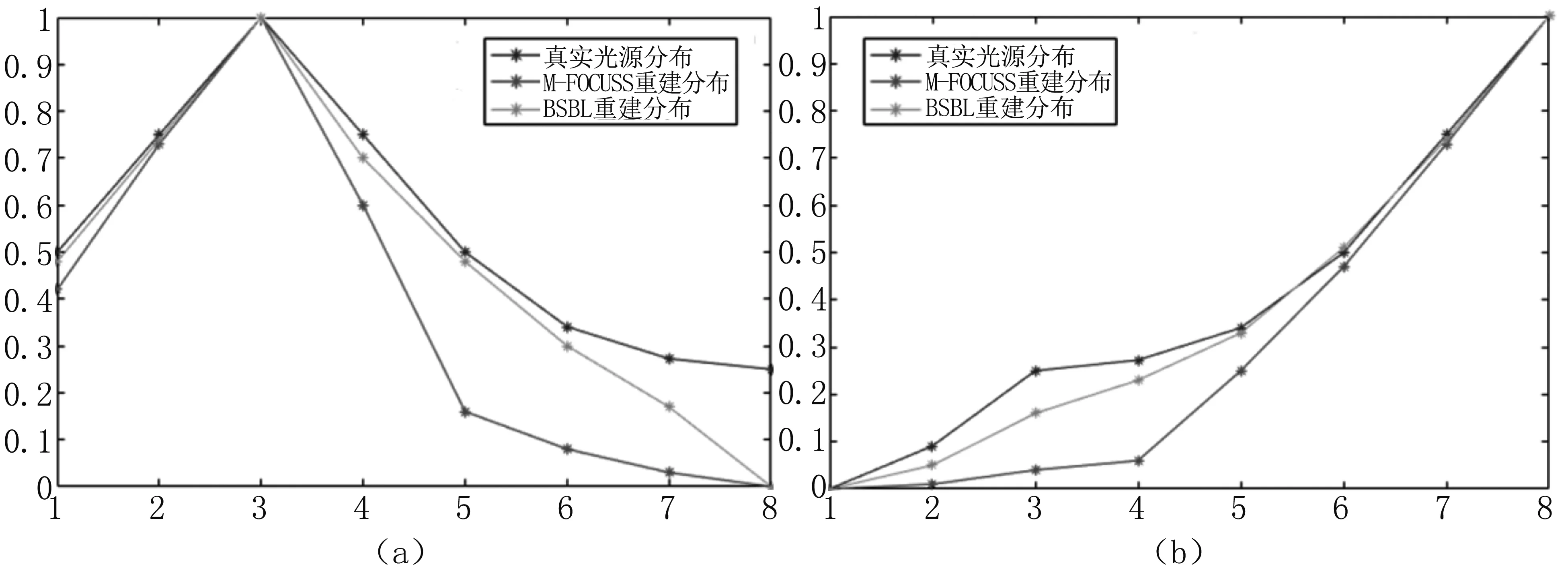
圖8 豬肉組織實驗動態熒光分離結果(a)、(b)分別為tube1、tube2的動態熒光濃度歸一化曲線Fig 8 Dynamic fluorescence separation results of pork tissue experiment(a),(b) are normalized curves of dynamic fluorescence concentration for tube1 and tube2 respectively.
本研究采用定位誤差和濃度偏差對M-FOCUSS算法和本研究算法重建結果進行評價,見表1。定位誤差為重建光源中心與真實光源中心差的歐式距離。從圖7和表1可以看出本研究算法在腫瘤定位精度和濃度偏差方面占據優勢,重建結果收斂性也比較好。

表1 重建效果對比
4 結論
本研究針對多目標動態熒光分子逆向重建存在稀疏性不足、定位精度低的問題,提出了基于塊稀疏貝葉斯學習的重建方法。該方法充分挖掘了信號的時空相關性信息和分塊稀疏特性,實現多目標動態熒光分子的稀疏重建。通過數值仿真和生物組織實驗驗證,本研究重建算法相較于傳統壓縮感知重構算法具有更高的定位精度和更好的魯棒性。

