基于科學思維水平層次,培養學生建模能力
——以“圓錐擺模型”為例

居 津

(江蘇省蘇州實驗中學，江蘇 蘇州 215011)

2018年1月,教育部正式發布了《普通高中物理課程標準(2017版)》(以下簡稱“高中課標2017版”)要求在教學中要讓學生體會建構物理模型的思維方法,理解物理模型的適用條件,能通過建構物理模型來研究實際問題,并明確指出引導學生經歷物理概念的建構過程和物理規律的形成過程,是發展科學思維的重要途徑．同時,高中課標2017版尤其關注學生物理學科核心素養的提升,將科學思維按學業質量要求進行了詳細的水平劃分,每一水平對于物理模型有不同的、明確的能力要求,具體如圖1表示.

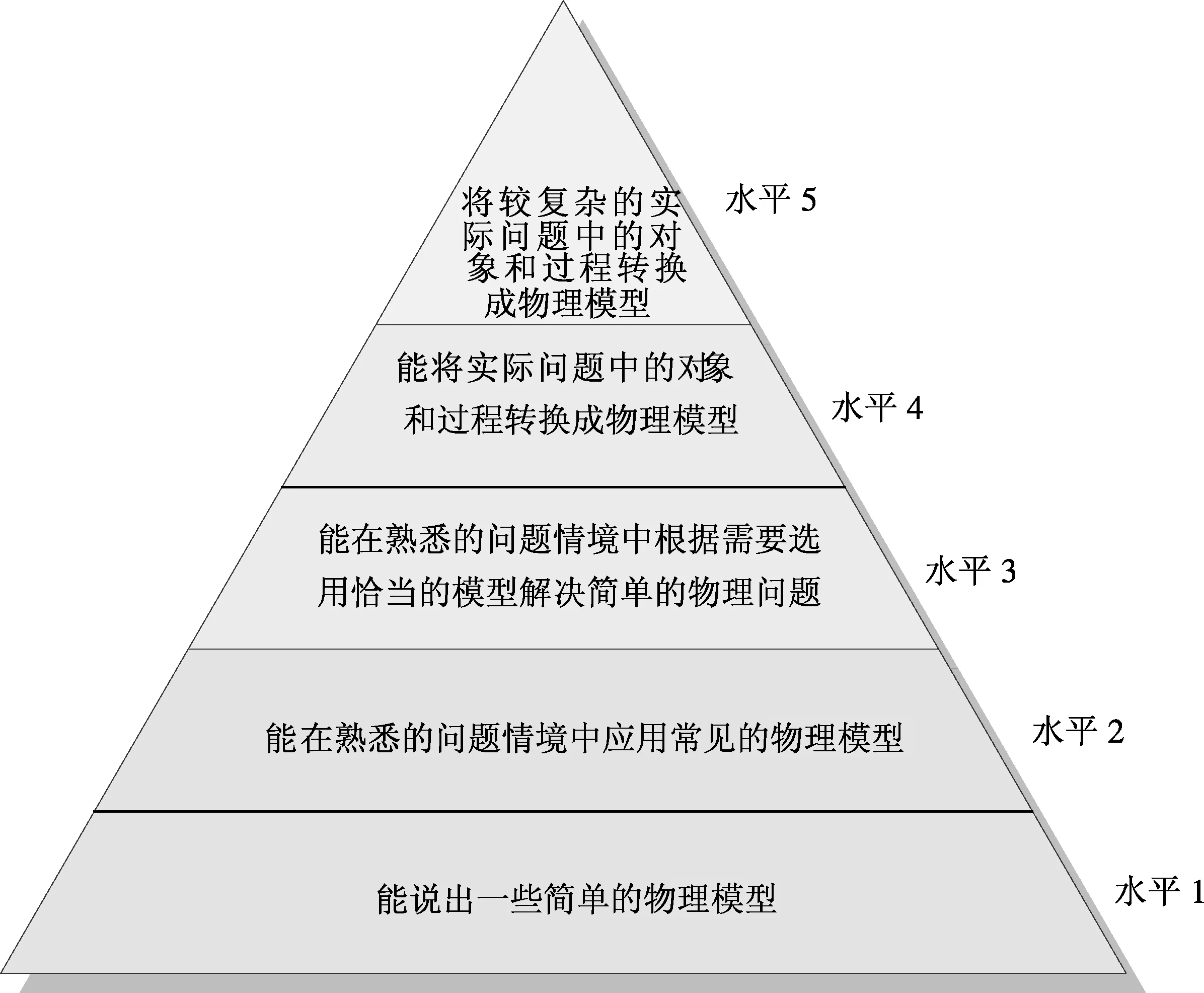
圖1

高中課標2017版的科學思維對于建構模型的要求劃分明確,但由于篇幅限制,課標中并未舉例說明如何進行教學實施.本文嘗試以“圓錐擺模型”為例,按5個水平要求序化物理教學,談談如何逐步提高學生的建模能力和問題解決能力．

1 認識物理模型——萌生建立

科學思維水平1要求學生能說出一些簡單的物理模型．著名科學家錢學森指出:模型即使通過對問題現象的分解,利用我們考慮得來的原理吸收一切主要的因素,略去一切次要的因素,所創造出來的一幅圖畫……高中物理涉及很多物理模型，如:勻變速直線運動,分子動理論等．要培養學生的科學思維能力,就建模、解決問題能力而言,最基本的就是需要了解物理模型的基本規律.我們姑且把此過程稱為萌生,即在學生腦中有物理模型的基本原理,以便于在遇到實際問題時可以提取相關信息,解決物理問題,提高學科核心素養．

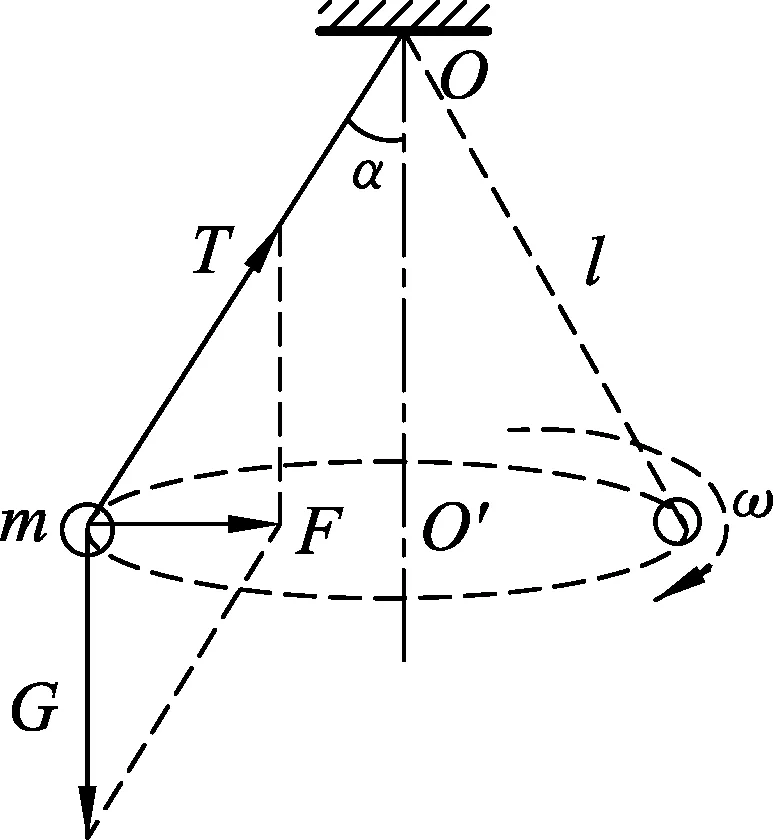
圖2

“圓錐擺模型”指細線一端系一小球,另一端固定于天花板,使小球以一定的速度在水平面內做勻速圓周運動,細線在空中所圍成的形狀類似于圓錐,這就制作成了一個“圓錐擺”． “圓錐擺模型”是勻速圓周運動中一個基本模型,如圖2．該模型中,小球受到重力G和繩中拉力T兩個力作用,這兩個力的合力F提供小球在水平面內做勻速圓周運動的向心力．設繩長為l,小球質量為m,懸線與豎直方向的夾角為α,則向心力F=mgtanα,對于勻速圓周運動的物體,其合外力提供向心力,可以得到

其中r=lsinα.可計算得到

以上是圓錐擺模型的基本規律,只有達到水平1,掌握最簡單的原理,萌生建立模型思想,才能達到更高的層次水平,進一步解決較為復雜的問題．

2 應用熟悉的物理模型——運用熟悉

掌握了最基本、最簡單的模型后,科學思維水平2要求學生能應用熟悉的物理模型．這就是第二層次即運用．對于這一層次的要求,學生應該能一眼辨識出實際問題與模型的共同點,并用基本物理模型和簡單的物理量轉化,解決相關問題．

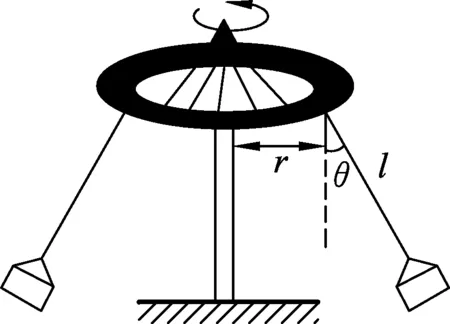
圖3

例1.兒童樂園里的游戲“空中飛椅”簡化模型如圖3所示,座椅通過鋼絲繩與頂端轉盤連接．已知正常工作時轉盤的轉速一定．設繩長為l,繩與豎直方向夾角為θ,座椅中人的質量為m．則下列說法正確的是

(A)l變長時,θ將變大.

(B)l變短時,θ將變大.

(C)m越大,θ越小.

(D)m越大,θ越大.

對于以上實際問題,與水平1的基本模型相比,有兩處相關變形:(1) 本例題中提到的勻速圓周運動相關物理量是轉速n;(2) 圓周運動的半徑為r′=lsinθ+r,因此,很快可以得到

在這一水平層次中,學生的科學思維能力略有提高,不僅要識記基本物理模型,還要在實際問題中應用物理模型,但實際問題與物理模型非常接近,不需要過多的比較或轉換．

3 選擇恰當的物理模型——分析理解

科學思維水平3要求學生能在熟悉的問題情境中,根據需要選用恰當的模型解決簡單的物理問題．這一水平要求明顯高于前一層次,重點在于選擇,這就需要將問題情境與學生頭腦中的眾多物理模型進行對比、比較,找出與實際問題最類似的模型,從而解決問題．

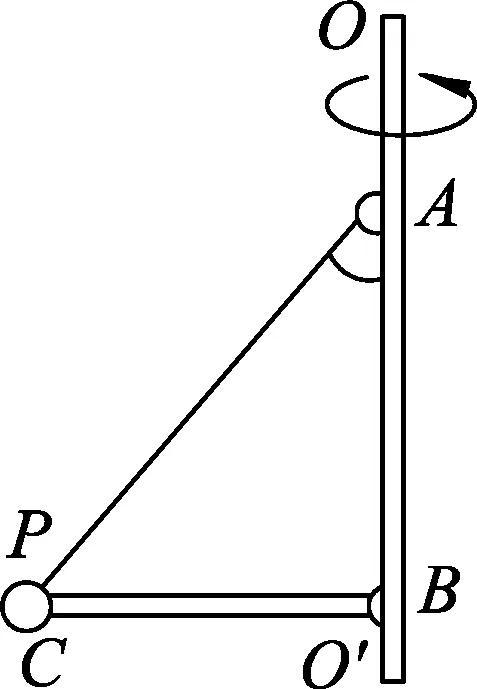
圖4

例2.如圖4所示,桿OO′是豎直放置的轉軸,水平輕桿BC的長為L,B端通過鉸鏈與軸相連(它們之間無摩擦),C端固定小球P,細線AC的一端固定在軸上的A點、另一端連在小球P上．已知小球的質量為m,細線AC與軸的夾角θ,重力加速度為g．求:(1)當系統處于靜止狀態時,桿BC對小球的彈力F1的大小;(2)當輕桿BC對小球的彈力為0時,系統轉動角速度ω的大小和細線上的彈力F2的大小;并據此判斷當ω變化時細線上的彈力大小是否變化．

在上述物理問題中,有輕桿、有細線,并不是典型的“圓錐擺模型”,第(1)問中,利用靜力學知識解決相關實際問題．第(2)問中,考察學生物理學科核心素養科學思維的模型對比能力．當桿中力為0時,小球在細線的作用下隨桿OO′發生轉動,由小球重力和細線中拉力的合力提供向心力,與“圓錐擺模型”的基本原理完全一致.這需要學生將此問題略作轉化,與頭腦中的眾多模型進行比較,并作出正確的選擇,最后將該模型運用到解決本問題中去．在這一層次中,學生需要分析所遇到的場景,對模型加以理解,才能更好地應用解決問題,達到這一層次的學生能力較上一層次有了進一步的提高．

4 將實際問題轉換成物理模型——轉換提高

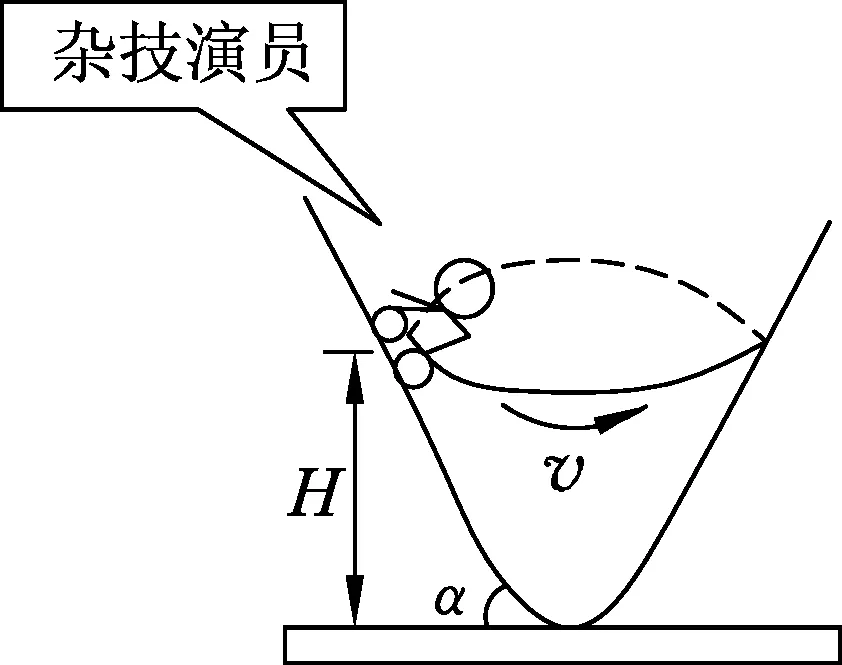
圖5

例3.蔡氏飛車走壁技藝由著名雜技藝術家蔡少武于20世紀50年代在遼寧省沈陽市創立,是一種在木桶或在環球進行飛車(一般為摩托車或自行車)走壁的高難度表演技藝,集體育與雜技融為一體．為沈陽市第一批市級非物質文化遺產,現仍有蔡氏后人傳承這一獨特技藝．此表演深受青少年的喜愛,表演者沿表演臺的側壁做勻速圓周運動,如圖5．若表演時雜技演員和摩托車的總質量不變,摩托車與側壁間沿側壁傾斜方向的摩擦力恰好為零,軌道平面離地面的高度為H,側壁傾斜角度α不變,則下列說法中正確的是

(A) 摩托車做圓周運動的H越高,向心力越大.

(B) 摩托車做圓周運動的H越高,線速度越大.

(C) 摩托車做圓周運動的H越高,向心力做功越多.

(D) 摩托車對側壁的壓力隨高度H變大而減小.

解決物理原始問題,情境教學是培養學生物理學科核心素養的重要渠道．而提高學生科學思維水平的重要表現就是能解決實際問題．物理是最貼近生活的一門學科,建立物理模型的最終目的也就是為了通過解決實際問題,提高學生的問題解決能力,培養關鍵能力．科學思維水平4要求學生能將實際問題轉化成相關物理模型．轉換過程一般可以分為以下幾個步驟.

4.1 排除干擾因素

上述實際問題中,“蔡氏飛車走壁技藝由著名雜技藝術家蔡少武于20世紀50年代在遼寧省沈陽市創立,是一種在木桶或在環球進行飛車(一般為摩托車或自行車)走壁的高難度表演技藝,集體育與雜技融為一體．為沈陽市第一批市級非物質文化遺產,現仍有蔡氏后人傳承這一獨特技藝”都屬于轉換干擾因素,在利用物理模型解決問題時,可以暫且不予理會．

4.2 提取重要信息

本題中的重要信息有4條:(1) 表演者做的是勻速圓周運動;(2) 軌道平面離地面高度不變,即圓周運動的半徑不變;(3) 傾角不變,表演者的受力不變．(4) 不受摩擦力作用．

4.3 加工類比

提取重要信息之后,就要對信息進行加工類比,演員受到重力G與斜面支持力F兩個力的作用.這兩個力的合力提供他做勻速圓周運動所需要的向心力,雖然表面上該問題與圓錐擺不同,但受力的本質是相同的,分析方法也相同．因此,解決這個實際問題,可以應用圓錐擺模型．

4.4 轉換應用

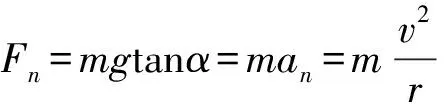
通過上述步驟,相信學生對于處理一般的實際問題有了大概的了解,科學思維水平也得到了再次的提高,建模能力和問題解決能力都得到了大大的鍛煉．

5 較復雜的實際問題轉換成物理模型——抽象領悟

科學思維的最高水平是能將較復雜的實際問題中的對象和過程轉換成物理模型．這一層次較上一層次而言,更接近于實際生活,學生遇到的情境更為復雜,學生所具備的能力不僅是轉化分析能力,還需要一定的抽象和領悟能力．

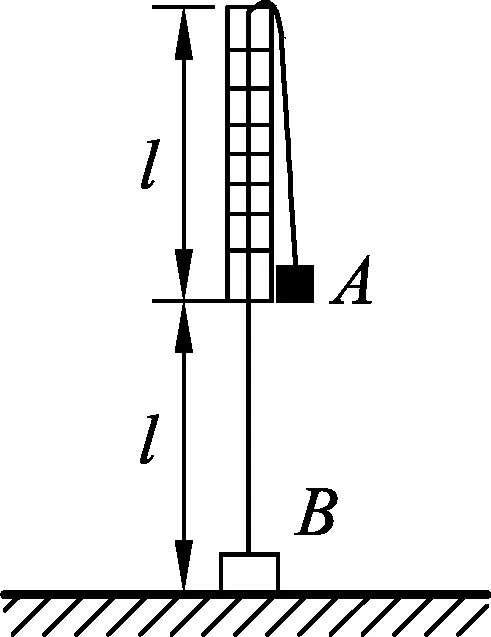
圖6

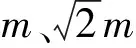
相對于水平4而言,水平5的問題情境更為復雜,但將實際問題轉化成物理模型的一般步驟仍然適用．排除無關干擾因素,提取重要信息后,不難發現,小球A最后在水平面內做勻速圓周運動,而向心力是由重力和繩中拉力提供的,由于物塊B處于靜止狀態,所以物塊物塊B的重力大小與繩中拉力大小相同．只要搞清楚此關鍵點,那么本問題也就迎刃而解了．此處不再贅述．

對于水平5的能力層次,要求學生具有一定的抽象概括能力,并加以領悟,這顯然是所有層次中要求最高的,要達到這個層次要求,必須有意識的在教學中從水平1開始逐步引導,讓學生熟悉各種物理模型的不同特點,并不斷加深鞏固,在簡單的實際問題中慢慢加深,從而達到解決復雜實際問題的能力,最終實現科學思維能力的培養,學科核心素養的提高!

以上是筆者基于科學思維水平劃分的物理建模能力要求所提出的的一點看法,希望起到拋磚引玉的作用,與廣大同仁一起探討如何提高學生學科核心素養,培養學生建模能力和問題解決能力.