在習題教學中培養學生的高階思維能力

吳 剛

(巴中市恩陽區恩陽中學,四川 巴中 636064))

高階思維是基于“復雜情境”問題分析而得到的“機制”和“結晶”[1].思維由低到高分為記憶、理解、應用、分析、評價和創造六個層級，其中前三個層級為低階思維；后三個層級為高階思維[2].低階思維是發展高階思維的基礎，高階思維是低階思維進入深度學習區后表現出來具有更高水平的思維過程和成果.在習題評講教學環節有意識地通過“一題多解”、“一題多變”、“數理結合”和“反思質疑”，把問題情境適當延寬一些，把思維觸覺適度拓深一些，促進學生對問題情境有更深入的理解、對物理過程有更透徹的分析，達到培養學生高階思維的能力和發展學生核心素養的目標.

1 一題多解

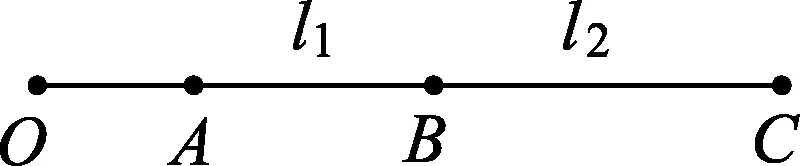
圖1

例1.已知O、A、B、C為同一直線上的四點，A、B間的距離為l1,B、C間的距離為l2，如圖1所示.一物體自O點由靜止出發，沿此直線做勻加速直線運動，依次經過A、B、C三點.已知物體通過AB段與BC段所用的時間相等，求O與A的距離.

設物體的加速度為a，經OA段的時間為t0，物體經AB段和BC段的時間均為t，O與A的距離為l，對物體經過OA段、OB段、OC段分別有

(1)

(2)

(3)

(4)

(5)

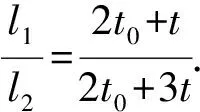
(6)

(7)

設物體在A點的速度為vA，則有

(1)

l1+l2=2vAt+2at2.

(2)

由(1)、(2)式得

l2-l1=at2.

(3)

3l1-l2=2vAt.

(4)

設O、A間的距離為l，則有

(5)

由(3)～(5)式聯立解得

解法3：利用v2=2as和v2=v02求解.

設A、B、C三點的速度分別為vA、vB、vC，則有

vA2=2al.

(1)

vB2-vA2=2al1.

(2)

vC2-vB2=2al2.

(3)

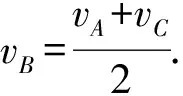
(4)

解法4：利用Δs=aT2求解.

由題意有l2-l1=at2.

(1)

(2)

vB2=2a(l+l1).

(3)

由(1)～(3)式聯立解得

解法5：利用v-t圖像求解.

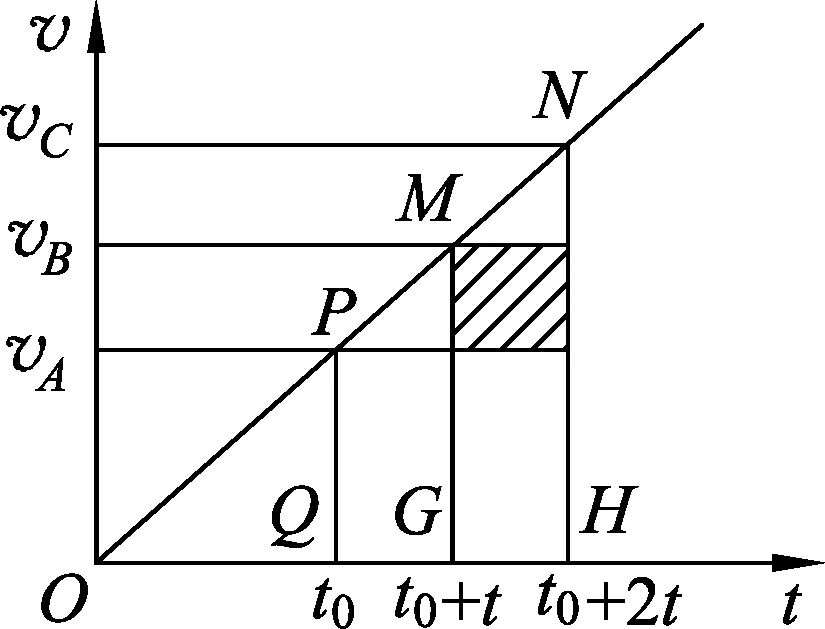
圖2

作出物體從O到C的v-t圖像，如圖2所示.設t0、t0+t、t0+2t時刻物體分別通過A、B、C3點，速度分別為vA、vB、vC.

由圖中“面積”的物理意義及三角形相似比(△OPQ∽△OMG)得

(1)

BC段比AB段多通過的位移可表示為(陰影面積)

l2-l1=(vB-vC)t.

(2)

梯形PNHQ的面積是AC段的位移，則有

l1+l2=vB·2t.

(3)

本題看似一道極常規的試題，卻隱含著重重思維障礙，對學生解方程組的數學能力要求極高.在解法1中，有效方程數少于未知量數，學生因缺乏計算技巧而不知如何聯立求解出最后結果.在解法2中，由(1)、(2)式得出(3)、(4)式，然后計算出A點速度，計算方法巧妙，學生很難想到.解法4則回避了這一難點，更顯靈活.通過“一題多解”，有助于培養學生對同一問題從多維角度分析、思考，開闊學生思路,達到發展學生的發散思維.

2 一題多變

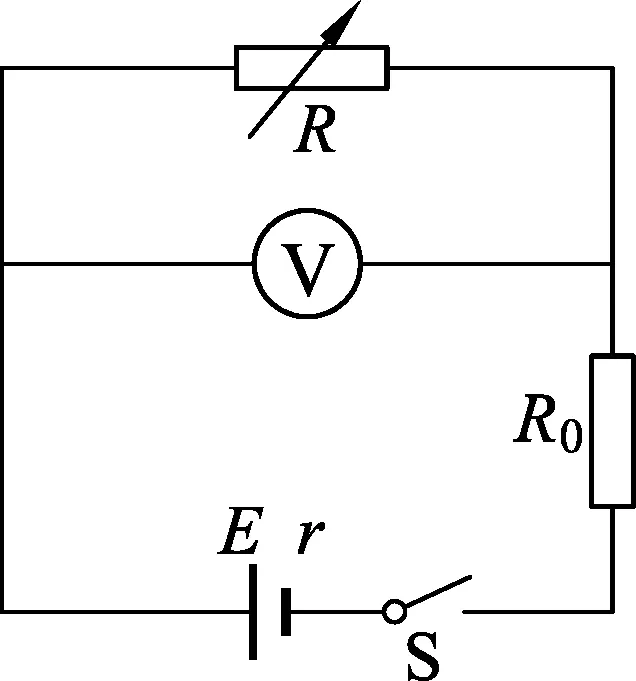
圖3

例2.如圖3所示，已知電源電動勢為6 V，內阻為1 Ω，保護電阻R0=0.5 Ω.求：當電阻箱R讀數為多少時，保護電阻R0消耗的電功率最大，并求這個最大值.

解析：保護電阻R0消耗的功率為

因R0和r是常量，而R是變量，所以R最小時，P0最大，即R=0時，

變式1.在其他條件不變的條件下，當電阻箱R讀數為多少時，電阻箱R消耗的電功率PR最大，并求這個最大值.

解析：電阻箱R消耗的電功率為

變式2.在例題中，若電阻箱R的最大值為3 Ω，R0=5 Ω，求：當電阻箱R讀數為多少時，電阻箱R的電功率最大，并求這個最大值.

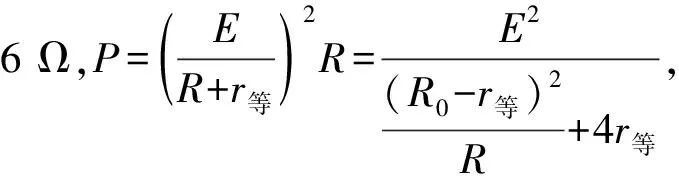
變式3.例題中條件不變，求電源的最大輸出功率.

解析:由

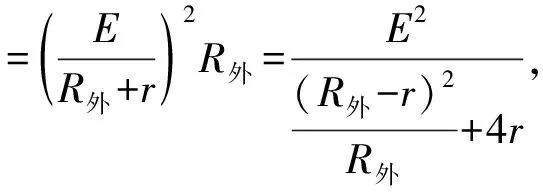
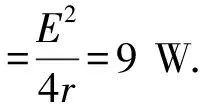
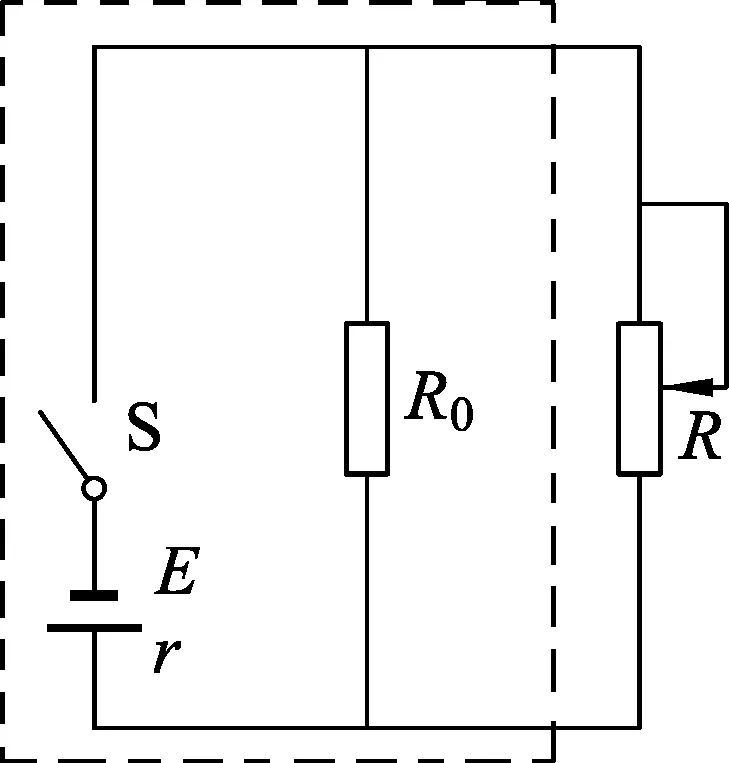
圖4

變式4.如圖4所示，電源電動勢E=2 V，內阻r=1 Ω，電阻R0=2 Ω，可變電阻的阻值范圍為0～10 Ω.求：可變電阻為多大時，R消耗的功率最大，最大值為多少？

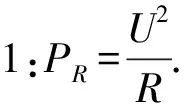
根據閉合電路歐姆定律，路端電壓為

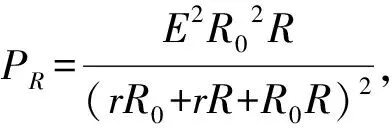
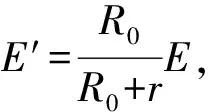
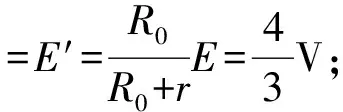
通過改變題目的條件或要求，對各種情況下功率的分析計算，使學生對知識的理解和應用能做到舉一反三、觸類旁通，起到“做好一題、帶活一片”的效果，對培養學生發散、創新思維能力大有裨益.

3 數理結合

例3.用輕繩懸掛一小球將小球拉至水平位置.然后放手使小球由靜止開始向下擺動，在小球擺至最低點的過程中重力對小球做功的功率

(A) 保持不變. (B) 不斷變大.

(C) 不斷變小. (D) 先變大后變小.

解析:這是一道高一物理必修2學習到瞬時功率計算時常考的題，一般用極限方法求解.小球在初位置速度為0，在最低點重力與速度垂直.由P=Fvcosα可知，小球在初、末位置重力的瞬時功率均為0，而在中間過程功率不是0.所以排除(A)、(B)、(C).下面對這個情景做一些深入定量分析，用于研究性學習，發展學生的高階思維能力.

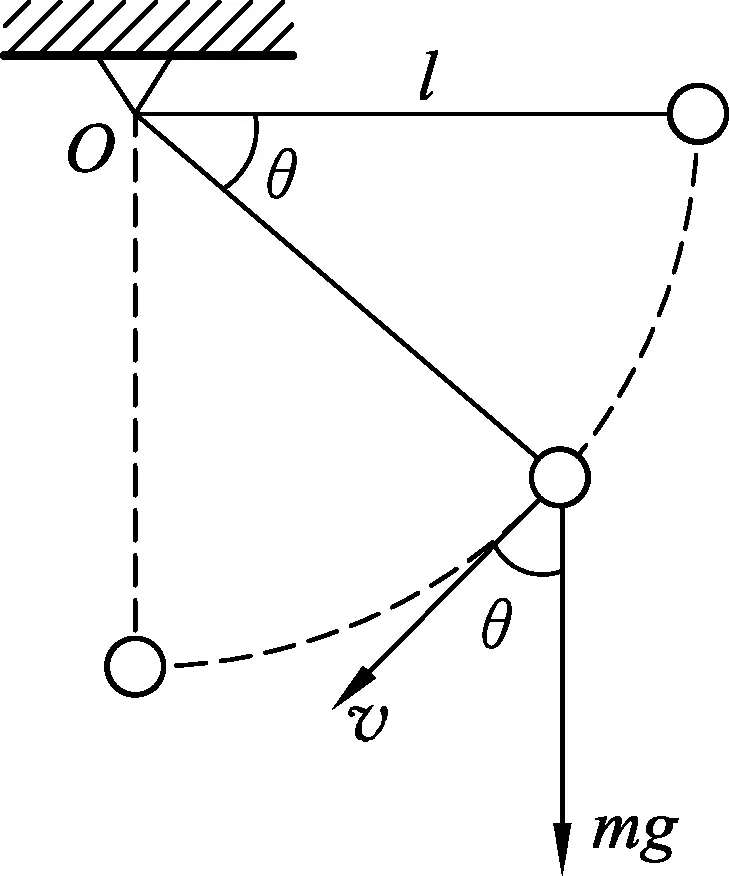
圖5

一般我們習慣從時間或空間維度觀察物理量的變化，即找到物理量隨時間變化的函數或隨位置坐標變化的函數.本情景中重力功率隨時間的關系很難找，但隨空間的關系比較容易找.如圖5所示，設擺長l、擺球質量m為定值，空間位置可用θ確定，找到重力的功率和θ的關系即可.

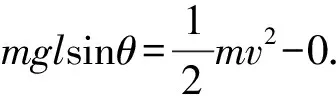
(1)

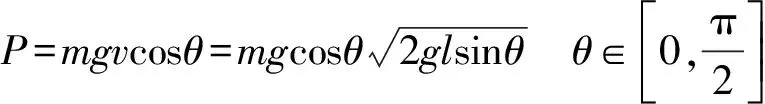
(2)

為看出P(θ)函數單調性，將上式整理得

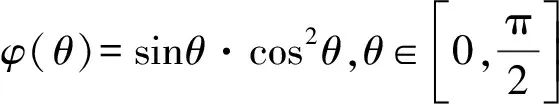
方法1：通過求導討論單調性.

φ′(θ)=cosθ·cos2θ-2sin2θcosθ=3cos3θ-2cosθ.

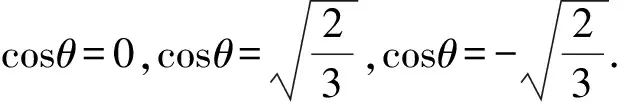
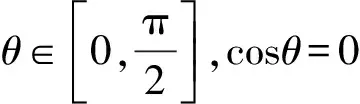
利用作圖軟件作出φ′(θ)=3cos3θ-2cosθ的圖像，如圖6所示.

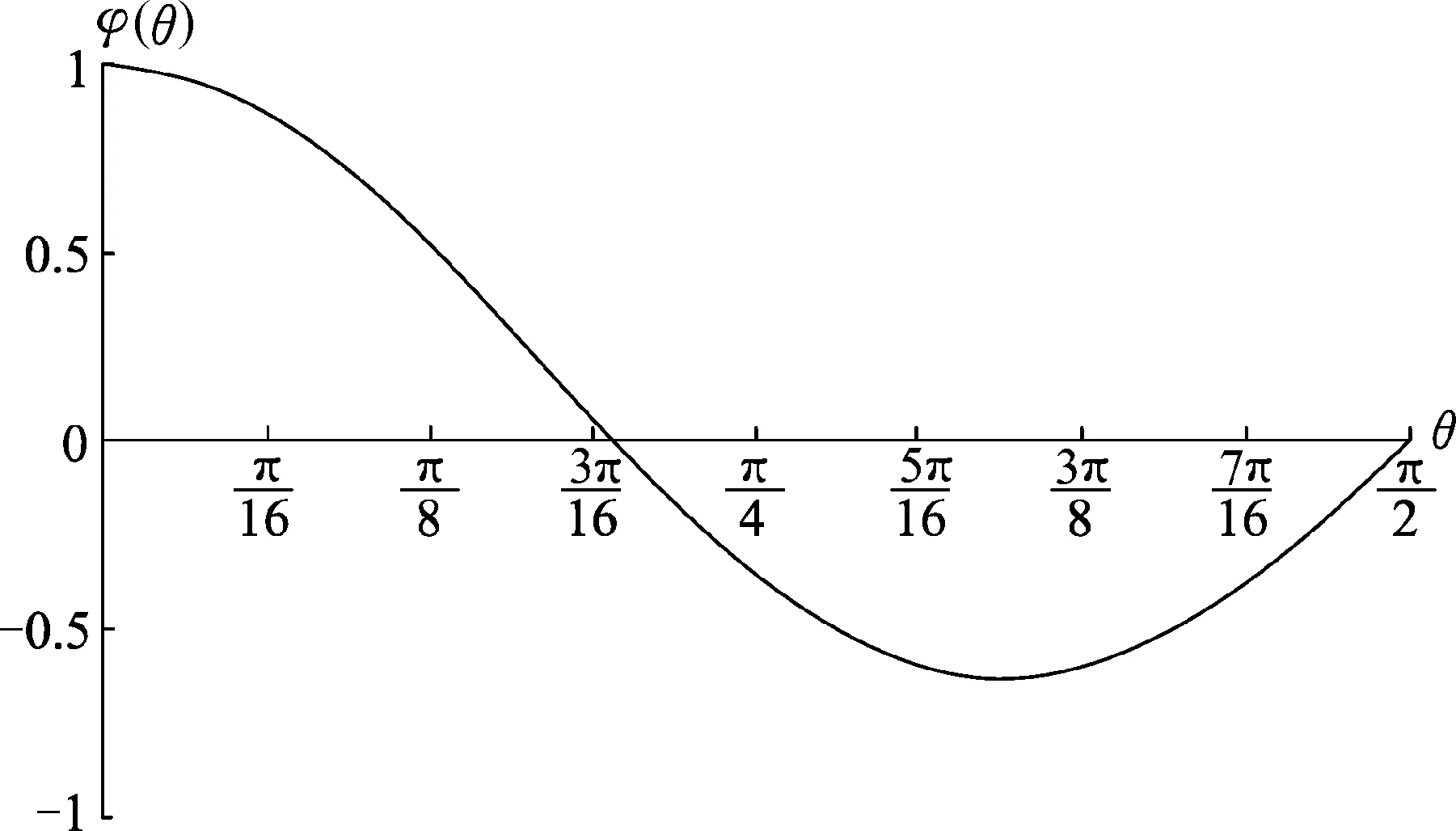
圖6

故φ(θ)=sinθ·cos2θ在θ≈35°有極大值，即重力的功率先變大后變小.

方法2：通過換元將三角函數轉化為多項式來討論單調性.

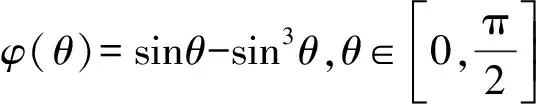
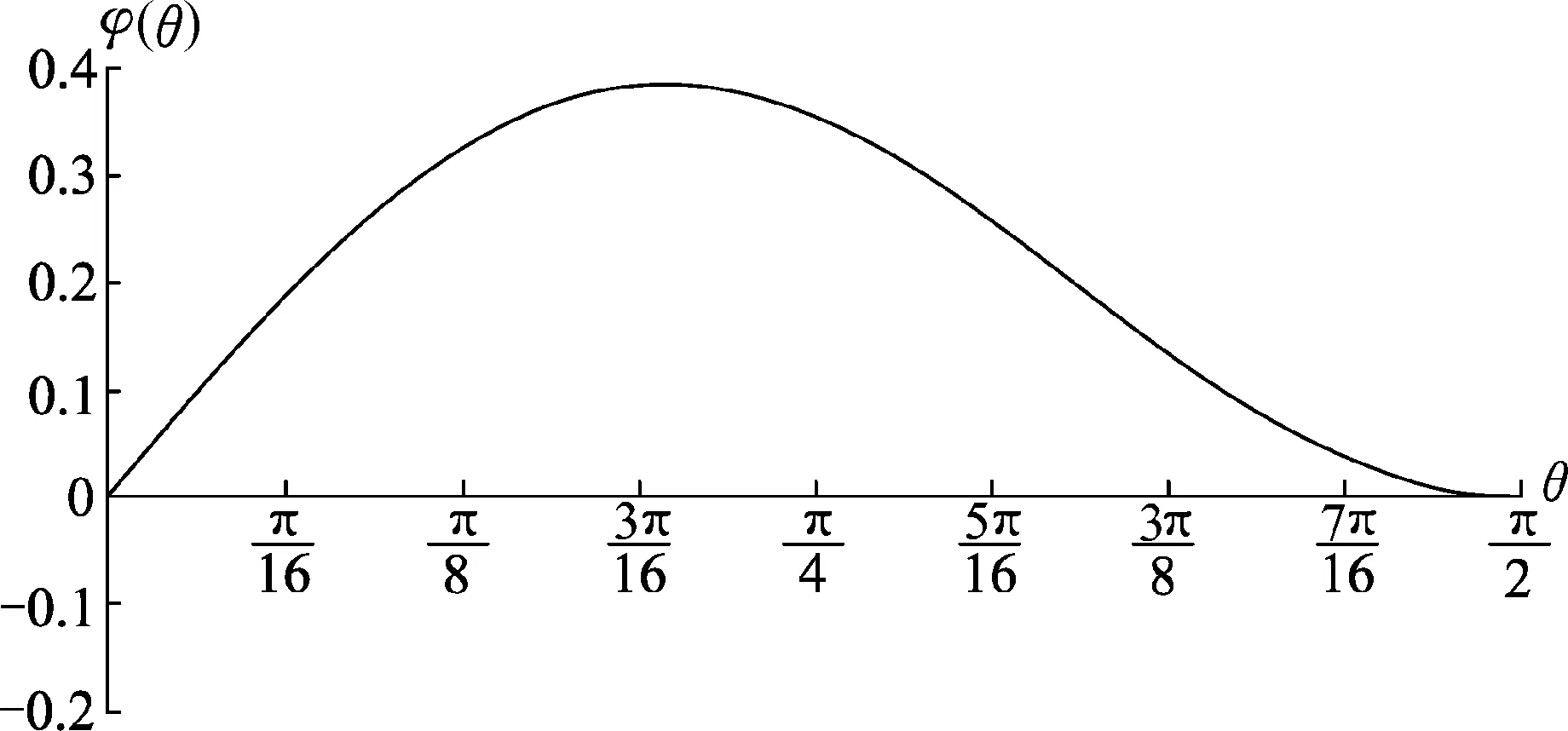
圖7

由圖像可看出θ≈35°時，φ(θ)=sinθ·cos2θ有極大值，同理得到重力的功率先變大后變小.

4 反思質疑

圖8

例4.木板向右水平運動時，上面輕放一木塊，如圖8所示.木塊與木板、木板與地面均不光滑.最大靜摩擦力近似等于滑動摩擦力，木塊和木板質量相等.木塊始終在木板上，則放上木塊后木板的v-t圖像正確的是

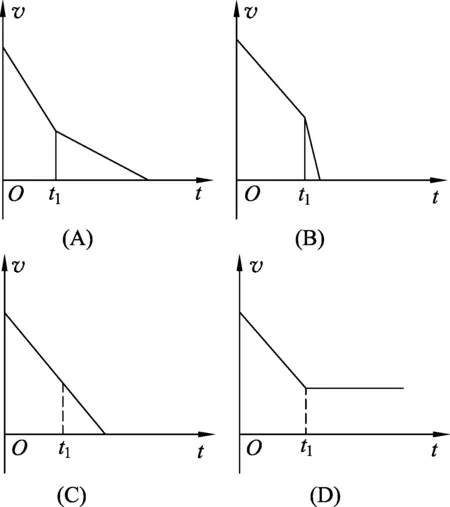
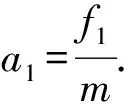
圖9

該學生選出的答案固然是正確的，但是解答過程并不完整.這道題涉及的物理過程還是比較復雜的，需要分情況討論，才能做出正確的解答.

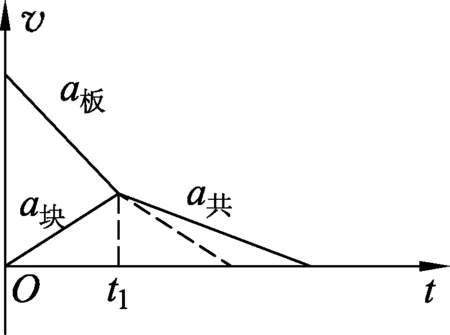
圖10

解析：兩者一起勻減速直線運動是有條件的，有可能木塊不能和木板一起做勻減速直線運動.下面進行分析討論：設木板上下表面的動摩擦因數分別為μ1、μ2.兩者有相對運動時，對木塊：a塊=μ1g，對木板：a板=μ1g+2μ2g，a塊

圖11

圖12

若μ1≤μ2，共速后兩者不可能相對靜止.通過分析可知，只能出現木塊相對木板向前運動的情況，即木塊受到與木板速度相反的滑動摩擦力作用，繼續減速，木塊和木板受力分析如圖11所示.對木塊有，a塊′=μ1g，對木板有，a板′=2μ2g-μ1g，由于a塊′=a塊

好多學生在做選擇題時，只求選出符合題意要求的選項，但有時其思維過程是不完整的，甚至是錯誤的.把學生在解答過程中存在的思維障礙暴露出來并加以剖析，讓學生對問題給予充分的質疑、辯論，以便能更好地培養學生嚴謹的學科思維和發展核心素養.