CFD數(shù)值模擬船舶在波浪中的回轉(zhuǎn)操縱運(yùn)動(dòng)

王建華 ，萬(wàn)德成

1上海交通大學(xué)海洋工程國(guó)家重點(diǎn)實(shí)驗(yàn)室，上海200240

2高新船舶與深海開發(fā)裝備協(xié)同創(chuàng)新中心，上海200240

3上海交通大學(xué)船舶海洋與建筑工程學(xué)院，上海200240

0 引 言

船舶操縱運(yùn)動(dòng)可以反映出船舶在航行過程中的機(jī)動(dòng)性、回轉(zhuǎn)特性和航向的糾偏能力。操縱性能的優(yōu)劣與船舶的航行安全和能耗息息相關(guān)，其重要性不言而喻。目前，船舶的操縱性能評(píng)估主要通過典型的操縱運(yùn)動(dòng)試驗(yàn)進(jìn)行，其中對(duì)船舶自由回轉(zhuǎn)操縱運(yùn)動(dòng)的數(shù)值模擬是評(píng)估船舶回轉(zhuǎn)性能的重要手段。船舶自由回轉(zhuǎn)操縱運(yùn)動(dòng)一般通過執(zhí)行目標(biāo)舵角，使船舶在舵提供的回轉(zhuǎn)力和力矩作用下實(shí)現(xiàn)回轉(zhuǎn)運(yùn)動(dòng)，典型的自由回轉(zhuǎn)操縱運(yùn)動(dòng)軌跡及特征參數(shù)如圖1所示。一般在船舶設(shè)計(jì)的初期階段，就需要評(píng)估所設(shè)計(jì)船舶的操縱運(yùn)動(dòng)特性，尤其是回轉(zhuǎn)特性，以指導(dǎo)船舶航行中的操作，保障船舶全壽期的安全性能。

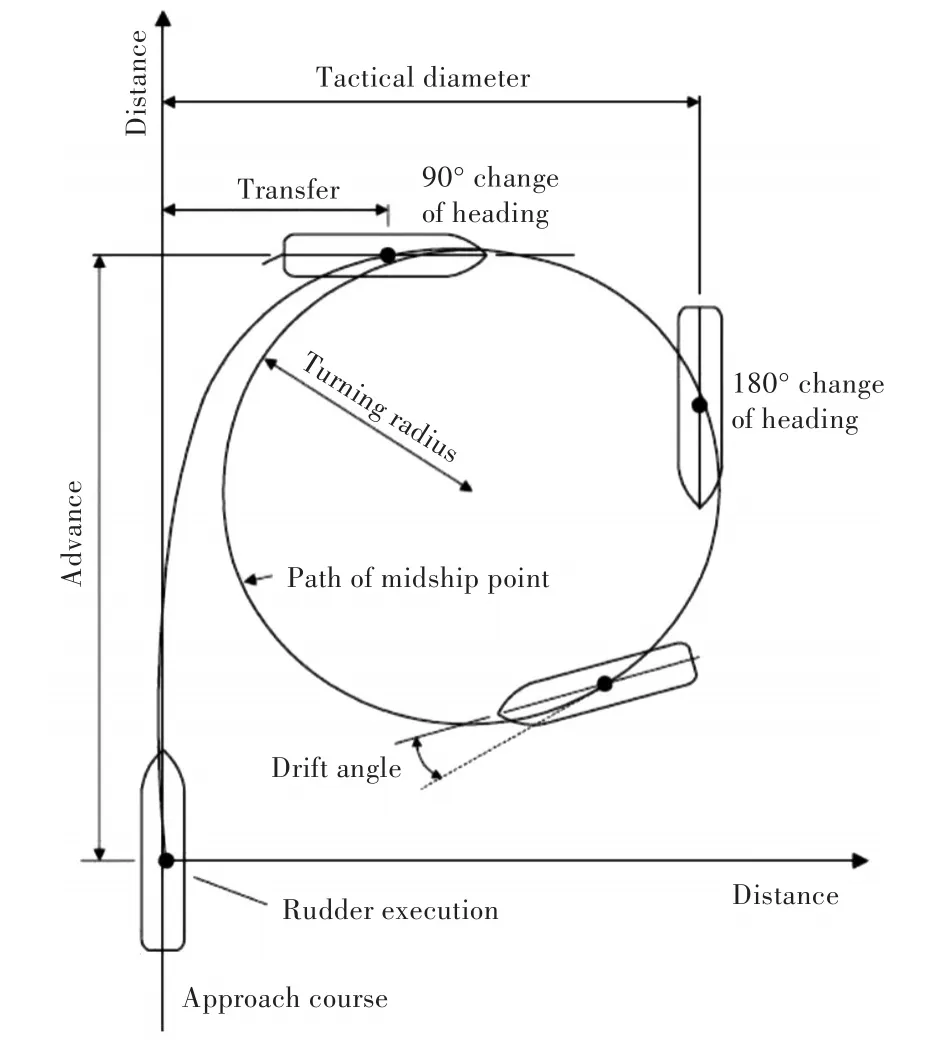
圖1 船舶自由回轉(zhuǎn)操縱運(yùn)動(dòng)軌跡及特征參數(shù)［1］Fig.1 Free turning maneuvering motion trajectory and main parameters of ship［1］

一般船舶操縱都是通過后舵操作，實(shí)現(xiàn)特定的操縱運(yùn)動(dòng)。因此，為了精確地評(píng)估船舶操縱運(yùn)動(dòng)特性，需要考慮到船—槳—舵的相互耦合作用。目前，應(yīng)用較為廣泛的船舶操縱性預(yù)報(bào)方法主要有船模試驗(yàn)方法和基于CFD的數(shù)值模擬方法。船模試驗(yàn)方法是目前應(yīng)用最廣泛也是最可靠的方法，尤其是近年來得益于試驗(yàn)裝置和方法的改進(jìn)，使得自航船模的操縱試驗(yàn)成為了可能。該方法可以通過在海洋工程波浪水池中或者天然湖泊中開展特定的操縱運(yùn)動(dòng)試驗(yàn)，來預(yù)報(bào)船舶操縱性能。但該方法需要較大的試驗(yàn)水池、精確的螺旋槳和舵控制系統(tǒng)以及用于測(cè)量船體六自由度運(yùn)動(dòng)的設(shè)備。此外，為真實(shí)還原船舶操縱運(yùn)動(dòng)中的實(shí)際流場(chǎng)，需要有與實(shí)際環(huán)境相似的試驗(yàn)水池，故船模試驗(yàn)方法的設(shè)備和試驗(yàn)成本高。而且，鑒于當(dāng)前的流場(chǎng)測(cè)量設(shè)備（如粒子圖像測(cè)速（PIV）等）普及性及適用性有限，試驗(yàn)中尚給不出操縱運(yùn)動(dòng)過程中船體、螺旋槳和舵周圍精細(xì)的流場(chǎng)結(jié)構(gòu)，并無法詳細(xì)分析在此過程中船舶的水動(dòng)力性能變化。

基于CFD的操縱運(yùn)動(dòng)數(shù)值模擬研究可分為約束船模操縱運(yùn)動(dòng)和自航船模操縱運(yùn)動(dòng)。前者通過結(jié)合操縱運(yùn)動(dòng)數(shù)學(xué)模型，依據(jù)數(shù)值模擬約束船模操縱運(yùn)動(dòng)得到各個(gè)水動(dòng)力導(dǎo)數(shù)，進(jìn)而對(duì)典型的船舶操縱性能進(jìn)行仿真，其被廣泛應(yīng)用于船舶操縱運(yùn)動(dòng)的數(shù)值模擬。Simonsen等［2］利用自主開發(fā)的求解器CFDShip-Iowa，數(shù)值模擬了靜態(tài)和動(dòng)態(tài)平面運(yùn)動(dòng)機(jī)構(gòu)（PMM）試驗(yàn)，并且分別采用CFD計(jì)算和試驗(yàn)測(cè)量得到的水動(dòng)力導(dǎo)數(shù)，根據(jù)分離型操縱性數(shù)學(xué)模型，對(duì)標(biāo)準(zhǔn)集裝箱（KCS）船模在靜水中的回轉(zhuǎn)操縱和Z形操縱試驗(yàn)進(jìn)行模擬。Guo和Zou［3］采用商業(yè)軟件 STAR CCM+數(shù)值模擬了標(biāo)準(zhǔn)船模ONRT的旋轉(zhuǎn)試驗(yàn)、靜態(tài)斜拖試驗(yàn)和純橫搖試驗(yàn)的操縱運(yùn)動(dòng)，數(shù)值回歸得到了操縱性水動(dòng)力導(dǎo)數(shù)值，運(yùn)用四自由度的操縱運(yùn)動(dòng)數(shù)學(xué)模型（MMG）仿真了船舶25°自由回轉(zhuǎn)和20/20 Z形操縱運(yùn)動(dòng)，預(yù)報(bào)的運(yùn)動(dòng)軌跡與試驗(yàn)值吻合較好，驗(yàn)證了采用CFD方法數(shù)值模擬約束船模操縱運(yùn)動(dòng)試驗(yàn)得到的操縱性導(dǎo)數(shù)值的可靠性。通過數(shù)值構(gòu)建船—槳—舵整體耦合運(yùn)動(dòng)求解模型，進(jìn)行自航船舶操縱運(yùn)動(dòng)的直接數(shù)值模擬，可以更精確地描述船舶操縱運(yùn)動(dòng)過程。

目前，隨著高性能計(jì)算機(jī)的快速發(fā)展以及重疊網(wǎng)格技術(shù)的逐步完善，直接數(shù)值模擬自航船模的操縱運(yùn)動(dòng)已成為現(xiàn)實(shí)。Carrica等［4］采用自主開發(fā)的水動(dòng)力學(xué)軟件CFDShip-Iowa V4，模擬了不同航速下（Fr=0.25，0.41）船舶自由回轉(zhuǎn)（35°舵角）和Z形操縱（20/20）特性，在數(shù)值計(jì)算中，利用動(dòng)態(tài)重疊網(wǎng)格技術(shù)處理大幅度的船舶操縱運(yùn)動(dòng)，并對(duì)波浪工況下的特性進(jìn)行計(jì)算，其數(shù)值預(yù)報(bào)的操縱性參數(shù)與試驗(yàn)值的誤差在10%以內(nèi)，指出簡(jiǎn)化的螺旋槳體積力模型是預(yù)報(bào)誤差產(chǎn)生的主要原因，該模型忽略了真實(shí)情況下螺旋槳旋轉(zhuǎn)導(dǎo)致的對(duì)船體運(yùn)動(dòng)的阻力及其受到的側(cè)向力影響等因素。Mofidi和 Carrica［5］采用同樣的求解器，但是考慮了真實(shí)情況下旋轉(zhuǎn)的螺旋槳，進(jìn)行了典型10/10 Z形操縱試驗(yàn)和修正型的15/1 Z形操縱試驗(yàn)的數(shù)值模擬，數(shù)值預(yù)報(bào)的船體運(yùn)動(dòng)及操縱性參數(shù)與試驗(yàn)結(jié)果吻合良好，并且對(duì)自航操縱運(yùn)動(dòng)過程中的詳細(xì)流場(chǎng)進(jìn)行了分析。Broglia等［6］和 Dubbioso等［7］分別進(jìn)行了單舵及雙舵情況下雙槳推進(jìn)船舶的自由回轉(zhuǎn)試驗(yàn)數(shù)值模擬，其中舵和船體運(yùn)動(dòng)采用動(dòng)態(tài)重疊網(wǎng)格進(jìn)行處理，將得到的船體運(yùn)動(dòng)軌跡與試驗(yàn)結(jié)果進(jìn)行對(duì)比，并比較了單舵和雙舵情況下自由回轉(zhuǎn)運(yùn)動(dòng)軌跡和回轉(zhuǎn)降速、漂角及橫搖等時(shí)歷曲線，分析了回轉(zhuǎn)運(yùn)動(dòng)全過程中的舵力和船體、附體的側(cè)向力變化，指出在雙槳情況下舵會(huì)強(qiáng)烈干擾螺旋槳受到的載荷。Shen等［8］基于開源CFD計(jì)算平臺(tái)OpenFOAM，開發(fā)了船舶水動(dòng)力學(xué)求解器 naoe-FOAM-SJTU［9-11］，引入了重疊網(wǎng)格模塊，并擴(kuò)展到船—槳—舵相互作用下的船舶自航［12］和操縱運(yùn)動(dòng)［13-15］模擬計(jì)算中，驗(yàn)證了采用非結(jié)構(gòu)化網(wǎng)格直接進(jìn)行帶螺旋槳、帶舵船舶的操縱運(yùn)動(dòng)數(shù)值模擬的可行性。

綜上所述，雖然結(jié)合重疊網(wǎng)格技術(shù)的CFD方法已經(jīng)廣泛應(yīng)用于船舶操縱運(yùn)動(dòng)的直接數(shù)值模擬，但是大部分研究都是針對(duì)靜水工況下的操縱運(yùn)動(dòng)，而海上航行的船舶經(jīng)常處于波浪環(huán)境中，因此很有必要開展波浪工況下操縱運(yùn)動(dòng)的精確預(yù)報(bào)，為船舶設(shè)計(jì)提供更為精確的數(shù)據(jù)支撐。本文將采用結(jié)合重疊網(wǎng)格技術(shù)的CFD求解器naoe-FOAM-SJTU，直接數(shù)值模擬帶螺旋槳、帶舵船舶在波浪中的自由回轉(zhuǎn)操縱運(yùn)動(dòng)，預(yù)報(bào)船舶在波浪中的操縱運(yùn)動(dòng)特性。通過數(shù)值計(jì)算船、槳、舵周圍精細(xì)的流場(chǎng)，分析船舶在自由回轉(zhuǎn)過程中的水動(dòng)力變化和船、槳、舵干擾以及波浪對(duì)船舶回轉(zhuǎn)性能的影響。

1 數(shù)值計(jì)算方法

1.1 流體計(jì)算控制方程

本文計(jì)算域流場(chǎng)求解的控制方程為非定常兩相不可壓縮的RANS方程：

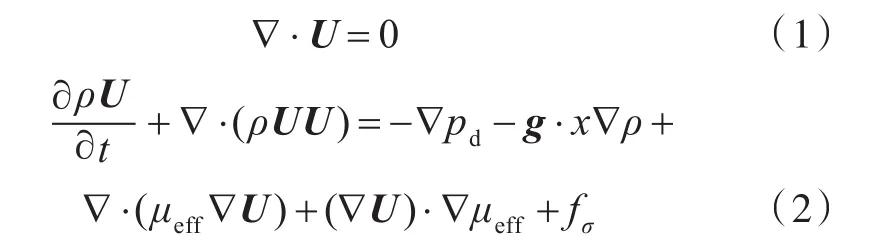
式中：▽為求散度；U為速度場(chǎng)；pd=p-ρg·x，為動(dòng)壓力，其數(shù)值等于總壓力值減去靜水壓力；ρ為液體或者氣體的密度；x為空間坐標(biāo)；t為時(shí)間；g為重力加速度向量；μeff=ρ(ν+νt)為有效動(dòng)力粘性，其中v為運(yùn)動(dòng)粘度，vt為渦粘度;fσ為表面張力項(xiàng)。

湍流模型采用SSTk-ω［16］，該模型兼具標(biāo)準(zhǔn)k-ω和k-ε模型的優(yōu)點(diǎn)，能夠保證壁面處和遠(yuǎn)流場(chǎng)求解的精確性和可靠性。自由面求解采用帶有人工可壓縮項(xiàng)的VOF（Volume of Fluid）方法［17］，兩相VOF輸運(yùn)方程定義為

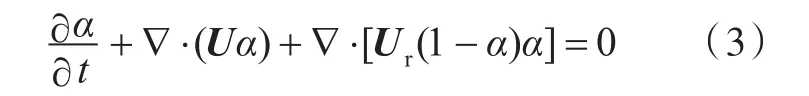
式中：Ur為用于壓縮界面的速度場(chǎng)；α為兩相流體的體積分?jǐn)?shù)，代表液體部分所占體積的百分比，取值范圍為0～1，0表示氣體，1表示水，介于0到1之間則表征為自由面位置。因此，通過體積分?jǐn)?shù)α便可以將兩相流規(guī)化為統(tǒng)一的流體域。

上述RANS方程（式（1）～式（2）），VOF輸運(yùn)方程（式（3））和湍流方程都采用有限體積法來進(jìn)行離散。采用OpenFOAM自帶的離散格式進(jìn)行方程離散，時(shí)間項(xiàng)采用隱式Euler格式，對(duì)流項(xiàng)采用二階TVD格式，耗散項(xiàng)采用中心差分格式，VOF方程中對(duì)流項(xiàng)采用Van Leer格式離散。流體控制方程求解中，速度壓力解耦采用PISO算法［18］。

1.2 自航船舶操縱運(yùn)動(dòng)控制模塊

船舶操縱一般都會(huì)有大幅度的船舶運(yùn)動(dòng)，傳統(tǒng)的變形網(wǎng)格在模擬物體大幅度運(yùn)動(dòng)時(shí)網(wǎng)格質(zhì)量會(huì)下降，影響求解精度；而重疊網(wǎng)格技術(shù)允許多個(gè)相互獨(dú)立的網(wǎng)格之間產(chǎn)生無約束的相對(duì)位移，在計(jì)算過程中能夠保證網(wǎng)格不發(fā)生變形，從而保證計(jì)算過程中網(wǎng)格的質(zhì)量，因此非常適用于帶槳、帶舵船舶操縱運(yùn)動(dòng)問題的數(shù)值求解。采用動(dòng)態(tài)重疊網(wǎng)格技術(shù)離散的船、槳、舵多級(jí)物體運(yùn)動(dòng)模型如圖2所示。螺旋槳和舵根據(jù)不同船體運(yùn)動(dòng)形式，可以按照指定的控制參數(shù)（如螺旋槳轉(zhuǎn)速、最大轉(zhuǎn)舵角度等），繞著旋轉(zhuǎn)軸進(jìn)行自身的旋轉(zhuǎn)運(yùn)動(dòng)，船體則在槳、舵自身運(yùn)動(dòng)以及船體受力情況下在自由面環(huán)境下做六自由度的運(yùn)動(dòng)。

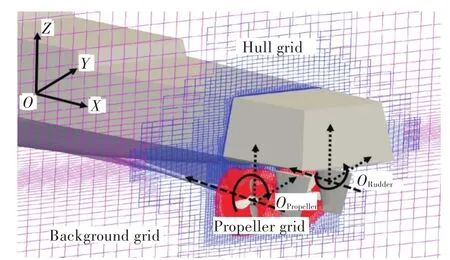
圖2 船—槳—舵多級(jí)物體運(yùn)動(dòng)示意圖Fig.2 Diagram of motions in ship-propeller-rudder system

依托重疊網(wǎng)格方法以及多級(jí)物體運(yùn)動(dòng)模塊，可以很方便地實(shí)現(xiàn)自航船舶的操縱運(yùn)動(dòng)控制，即通過對(duì)舵角的控制，實(shí)現(xiàn)特定船舶操縱運(yùn)動(dòng)的數(shù)值模擬。35°滿舵向右舷進(jìn)行自由回轉(zhuǎn)操縱運(yùn)動(dòng)的舵角控制方程為

式中：δ(t)為舵角；k為轉(zhuǎn)舵速率；tp表征進(jìn)行回舵的時(shí)刻，從而結(jié)束回轉(zhuǎn)運(yùn)動(dòng)，即何時(shí)回到初始零度舵角。在起始時(shí)刻，按照轉(zhuǎn)舵速率k進(jìn)行轉(zhuǎn)舵直到滿舵狀態(tài)，之后維持此舵角完成回轉(zhuǎn)操縱運(yùn)動(dòng)，根據(jù)模擬需求進(jìn)行回舵操作，結(jié)束回轉(zhuǎn)運(yùn)動(dòng)。

1.3 區(qū)域造波方法

區(qū)域造波方法與速度入口邊界造波方法直接的區(qū)別就是前者不僅需要邊界造波，同時(shí)還需要在特定的區(qū)域范圍內(nèi)對(duì)流場(chǎng)進(jìn)行改造。具體實(shí)現(xiàn)方式是通過采用松弛區(qū)域，保證外部邊界處沒有波浪反射，同時(shí)還能夠確保計(jì)算域內(nèi)部的波浪反射不會(huì)對(duì)造波邊界產(chǎn)生干擾，這也是邊界造波方法所不具備的特點(diǎn)。本文采用開源造波工具包waves2Foam［19］在移動(dòng)計(jì)算域中進(jìn)行波浪場(chǎng)生成。采用環(huán)形造波區(qū)，如圖3所示，進(jìn)行回轉(zhuǎn)操縱運(yùn)動(dòng)過程中的波浪生成，環(huán)形區(qū)域中通過松弛方式即可實(shí)現(xiàn)造波，同時(shí)也能完成消波。該造波區(qū)在計(jì)算中可以跟隨計(jì)算域進(jìn)行移動(dòng)，因此可以保證波浪在船舶進(jìn)行360°回轉(zhuǎn)運(yùn)動(dòng)過程中可以傳播到整個(gè)計(jì)算域中。圖中，L為船長(zhǎng)。

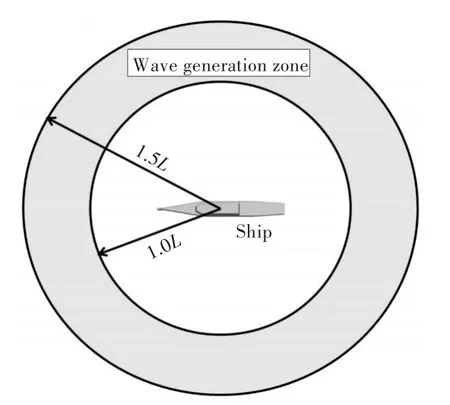
圖3 區(qū)域造波圖示Fig.3 Diagram of wave generation zone

2 計(jì)算模型和工況

本文計(jì)算船型采用全附體雙槳、雙舵的ONRT船模，該船模是被廣泛應(yīng)用于CFD驗(yàn)證的標(biāo)準(zhǔn)船型，被列為Tokyo2015 CFD研討會(huì)上的自航模問題的標(biāo)準(zhǔn)船型。對(duì)于該船型，有非常豐富的操縱試驗(yàn)數(shù)據(jù)，從而可以驗(yàn)證當(dāng)前數(shù)值預(yù)報(bào)手段的可靠性。船體的幾何模型如圖4所示。船體的主尺度如表1所示。

圖4 ONRT船幾何模型Fig.4 Geometry model of ONR Tumblehome ship

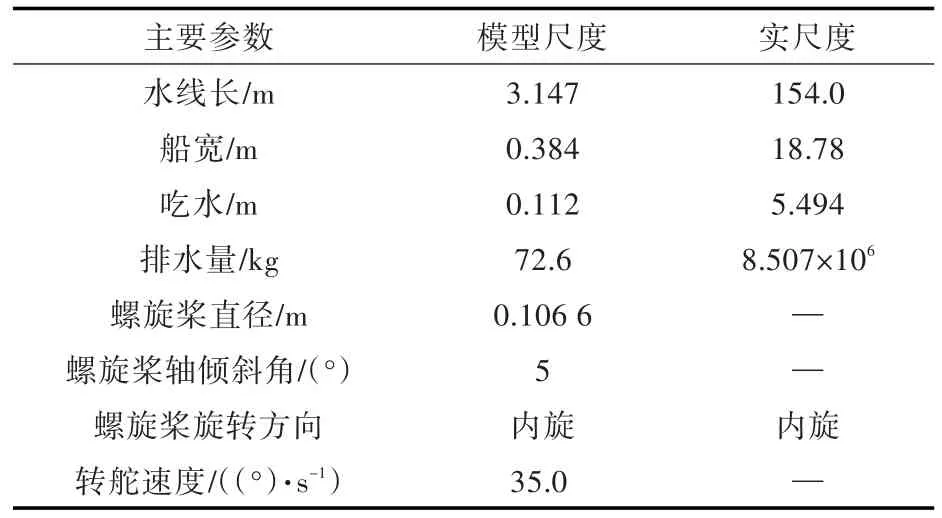
表1 ONRT船體模型主尺度Table 1 Main particulars of ONR Tumblehome ship model

數(shù)值計(jì)算中采用重疊網(wǎng)格方法進(jìn)行船、槳、舵網(wǎng)格的直接劃分，重疊網(wǎng)格的布置如圖5所示。計(jì)算域共分為6部分，即背景網(wǎng)格、船體周圍網(wǎng)格、2套螺旋槳網(wǎng)格和2套舵的網(wǎng)格，劃分完成的網(wǎng)格如圖6所示，計(jì)算網(wǎng)格總數(shù)量為711萬(wàn)。

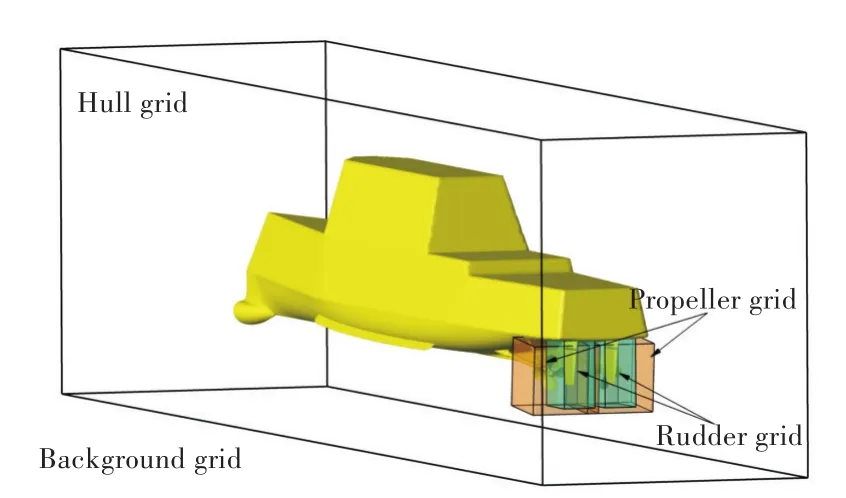
圖5 重疊網(wǎng)格布置Fig.5 Overset grid arrangement

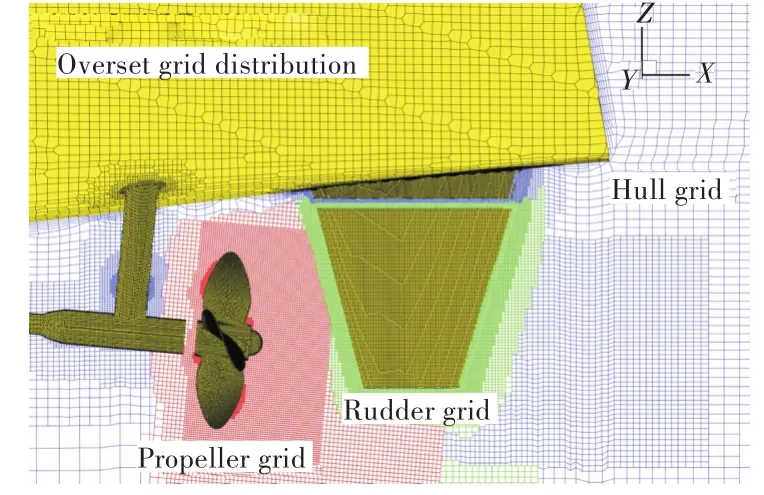
圖6 槳和舵周圍網(wǎng)格分布Fig.6 Local grid distribution around twin propellers and rudders

本文進(jìn)行了在35°舵角下，船舶在波浪中的自由回轉(zhuǎn)操縱運(yùn)動(dòng)的直接數(shù)值模擬，船舶初始航速為1.11 m/s，對(duì)應(yīng)于Fr=0.2，數(shù)值計(jì)算中螺旋槳的轉(zhuǎn)速設(shè)置為對(duì)應(yīng)于這個(gè)航速下的模型自航點(diǎn)值，為 529.14 r/min［13］。入射波浪根據(jù) IIHR 的試驗(yàn)［20］進(jìn)行設(shè)置，入射波浪的波長(zhǎng)λ等于船長(zhǎng)LWL，波陡H λ為 0.02。

3 波浪中船舶自由回轉(zhuǎn)數(shù)值模擬結(jié)果分析

波浪中的自由回轉(zhuǎn)操縱運(yùn)動(dòng)數(shù)值模擬從最終穩(wěn)定的自航數(shù)值計(jì)算開始，然后開始放開船舶的六自由度運(yùn)動(dòng)，與試驗(yàn)的一致，均在入射波浪的波峰到達(dá)船艏時(shí)進(jìn)行操舵，舵按照自由回轉(zhuǎn)操縱運(yùn)動(dòng)進(jìn)行控制。所有數(shù)值計(jì)算均在上海交通大學(xué)船海計(jì)算水動(dòng)力學(xué)研究中心高性能計(jì)算集群進(jìn)行，采用40個(gè)進(jìn)程并行計(jì)算，計(jì)算時(shí)間步長(zhǎng)為Δt=0.000 5 s，對(duì)應(yīng)于每個(gè)時(shí)間步螺旋槳轉(zhuǎn)過1.5°。完成波浪中的自由回轉(zhuǎn)操縱運(yùn)動(dòng)共耗時(shí)1 206 h，對(duì)應(yīng)于155 000個(gè)時(shí)間步。

圖7所示為數(shù)值預(yù)報(bào)的波浪中船舶自由回轉(zhuǎn)得到的運(yùn)動(dòng)軌跡以及與試驗(yàn)值［17］的對(duì)比。從圖中可以看出，當(dāng)前的數(shù)值預(yù)報(bào)結(jié)果與試驗(yàn)結(jié)果吻合較好，但是數(shù)值預(yù)報(bào)的回轉(zhuǎn)圈會(huì)比試驗(yàn)的結(jié)果更大，這主要是由于數(shù)值計(jì)算中為了保證重疊網(wǎng)格間足夠的插值單元，而對(duì)舵的幾何模型進(jìn)行了修正，減小了有效的舵面積，因此使得舵效減小。此外，從圖中還可以看出，在船舶航向角改變90°和270°時(shí)，回轉(zhuǎn)曲線會(huì)產(chǎn)生明顯的波動(dòng)現(xiàn)象。圖8所示為對(duì)應(yīng)的局部放大對(duì)比圖，在對(duì)應(yīng)的2個(gè)時(shí)間段，船舶的運(yùn)動(dòng)軌跡會(huì)產(chǎn)生明顯波動(dòng)，并且試驗(yàn)和CFD預(yù)報(bào)結(jié)果都顯示有這一現(xiàn)象。數(shù)值計(jì)算得到的波動(dòng)幅值明顯小于試驗(yàn)中的波動(dòng)值，這也說明了CFD模擬中船舶的回轉(zhuǎn)性較試驗(yàn)稍差，這也解釋了圖7中數(shù)值預(yù)報(bào)的船舶回轉(zhuǎn)圈更大的原因。

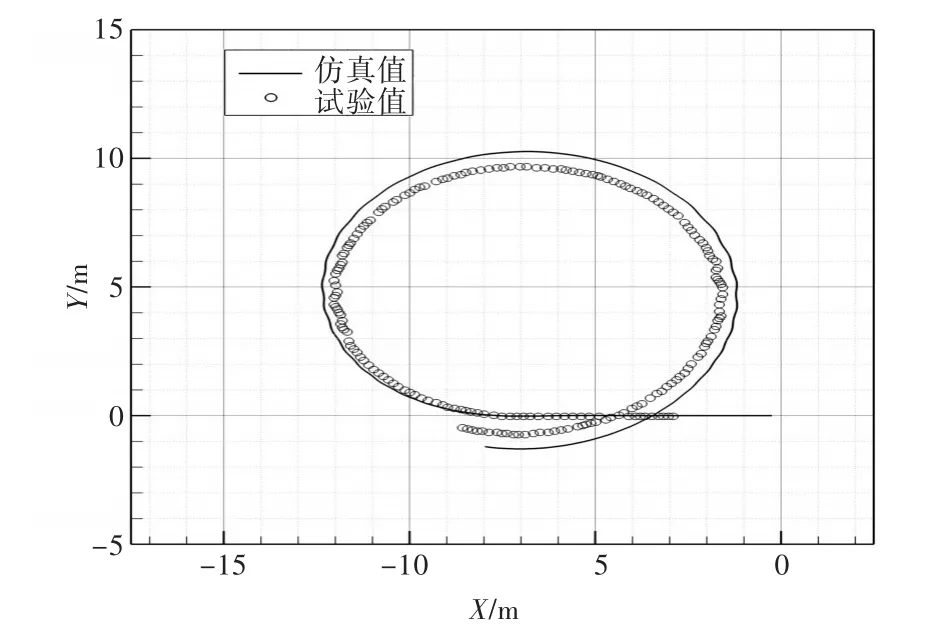
圖7 回轉(zhuǎn)圈軌跡對(duì)比Fig.7 Comparison of turning circle trajectory

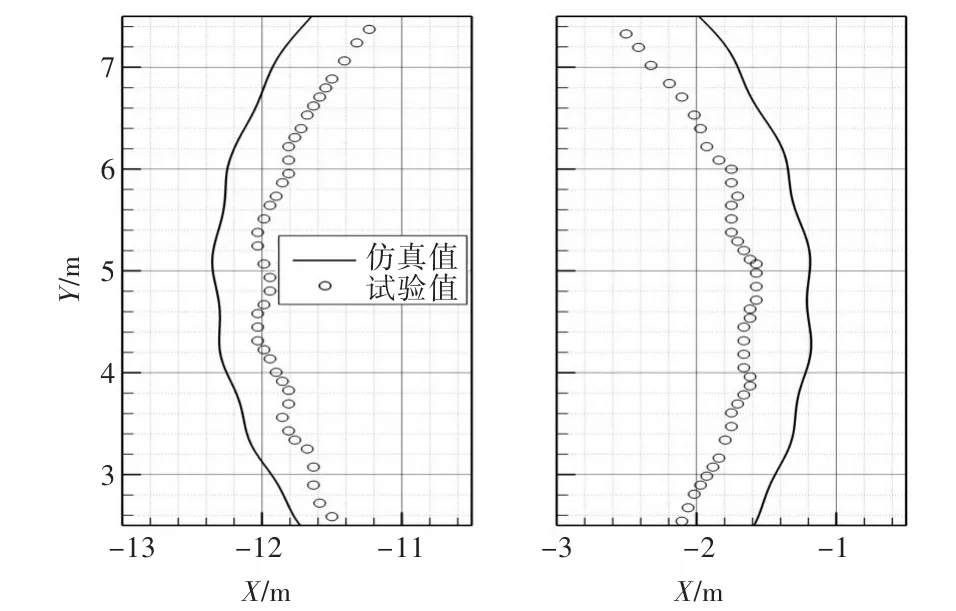
圖8 局部回轉(zhuǎn)運(yùn)動(dòng)對(duì)比Fig.8 Local comparison of trajectory

數(shù)值預(yù)報(bào)的船舶回轉(zhuǎn)圈特征參數(shù)及其與試驗(yàn)值［20］的對(duì)比如表2所示。

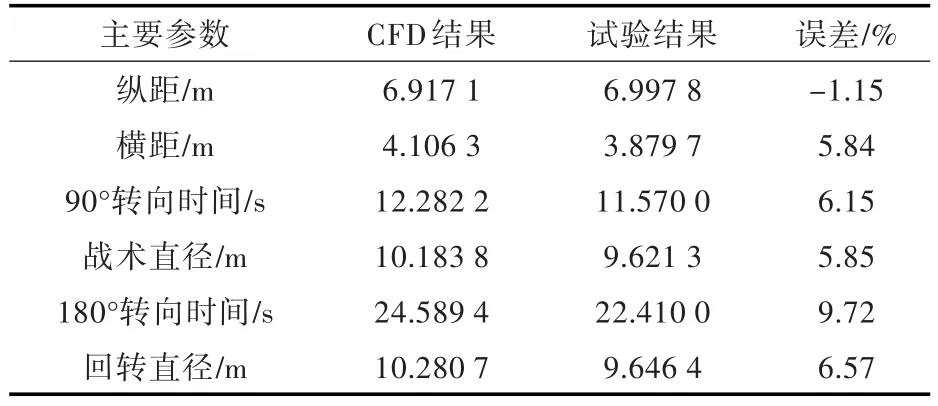
表2 回轉(zhuǎn)圈軌跡特征參數(shù)對(duì)比Table 2 Comparison of main parameters of turning circle trajectory

仿真過程中，為了保證對(duì)比的可靠性，對(duì)時(shí)間尺度進(jìn)行了調(diào)整，使得CFD模擬和物理試驗(yàn)滿足在同一個(gè)時(shí)刻執(zhí)行轉(zhuǎn)舵操作。從表中的對(duì)比結(jié)果可以看出，所有特征參數(shù)與試驗(yàn)值的誤差均在10%以內(nèi)，當(dāng)前的數(shù)值計(jì)算可以較高的精度預(yù)報(bào)出波浪中自由回轉(zhuǎn)船舶的操縱運(yùn)動(dòng)特性。

圖9所示為數(shù)值預(yù)報(bào)船舶在波浪中自由回轉(zhuǎn)過程中六自由度運(yùn)動(dòng)的時(shí)歷曲線。從圖中可以看出，船舶的垂蕩、縱搖和橫搖運(yùn)動(dòng)會(huì)產(chǎn)生較為明顯的波頻振蕩特性（圖9（a），（b）（c））。另外，由于回轉(zhuǎn)運(yùn)動(dòng)過程中船舶遭遇的浪向角也在時(shí)刻變化，因此在高頻的波頻運(yùn)動(dòng)下還存在由于回轉(zhuǎn)操縱運(yùn)動(dòng)導(dǎo)致的低頻波動(dòng)。整個(gè)回轉(zhuǎn)運(yùn)動(dòng)過程中，最大的縱搖幅值可達(dá)2.5°，橫搖運(yùn)動(dòng)的幅度為-4.4°～8°。此外，從橫搖運(yùn)動(dòng)的時(shí)歷曲線（圖9（c））可以看出，由于波浪導(dǎo)致的橫搖運(yùn)動(dòng)幅值較由于初始操舵導(dǎo)致的橫搖運(yùn)動(dòng)更大。而3個(gè)平面的運(yùn)動(dòng)，縱蕩、橫蕩和艏搖運(yùn)動(dòng)則展現(xiàn)較小的波頻運(yùn)動(dòng)特性。從艏搖運(yùn)動(dòng)的曲線（圖9（d））上可以看出較小的波動(dòng)，這也可能導(dǎo)致了圖8中展現(xiàn)的平面運(yùn)動(dòng)軌跡中的局部波動(dòng)。

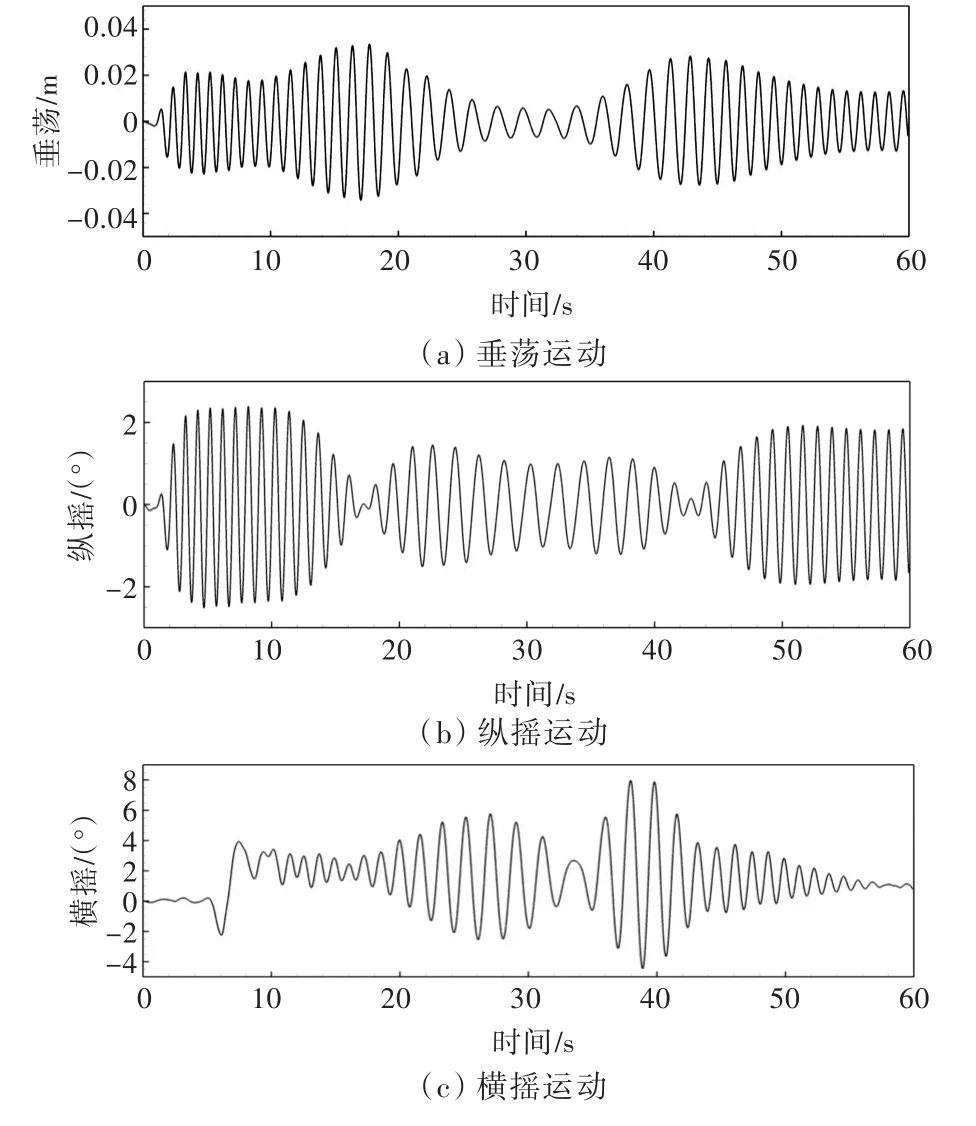
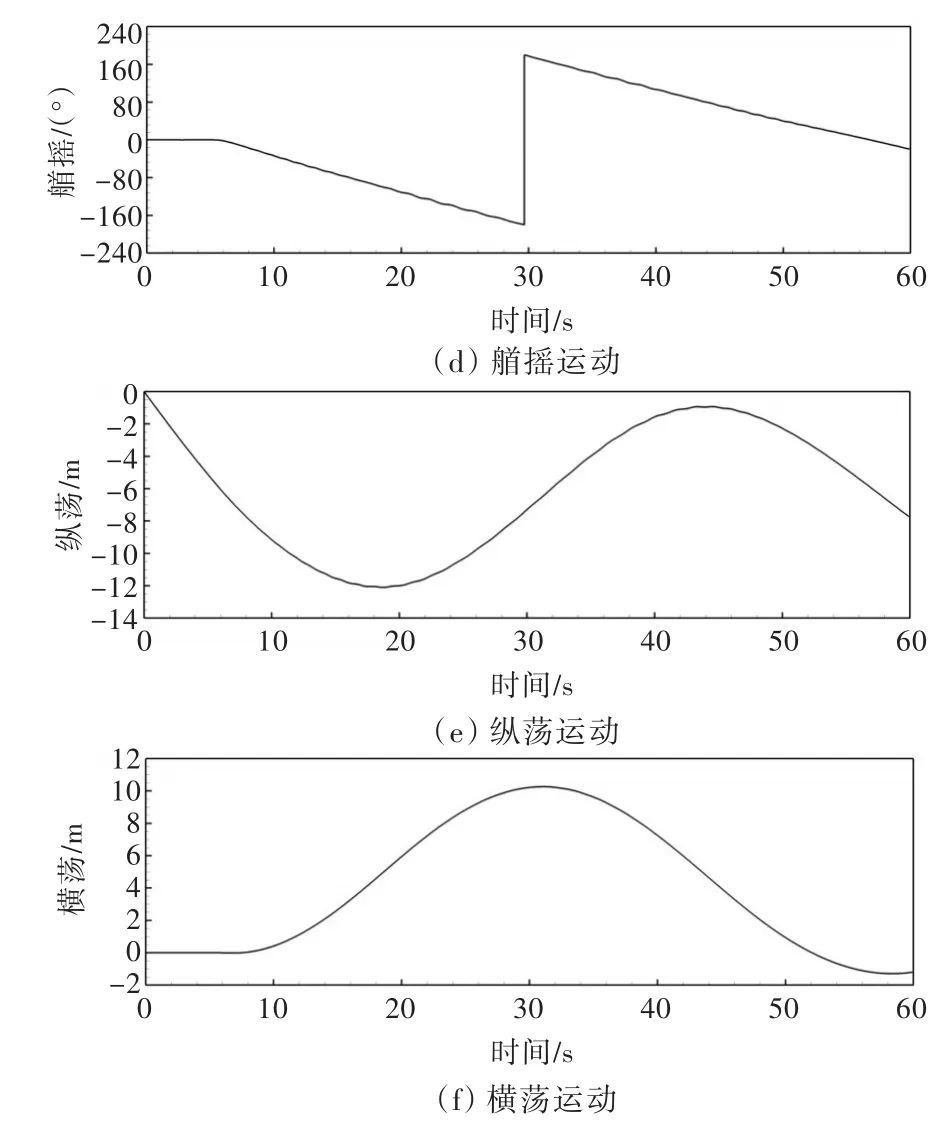
圖9 波浪中自由回轉(zhuǎn)操縱中船舶六自由度運(yùn)動(dòng)時(shí)歷曲線Fig.9 Time history curves of ship motions for turning circle maneuvering in waves

圖10所示為船舶在波浪中自由回轉(zhuǎn)運(yùn)動(dòng)過程中的航速以及艏搖速率的變化曲線。從圖中可以看出，波浪中的船舶在回轉(zhuǎn)運(yùn)動(dòng)過程中會(huì)出現(xiàn)明顯的回轉(zhuǎn)降速現(xiàn)象，并且最大降速可達(dá)40%。初始的航速降低是由于轉(zhuǎn)舵導(dǎo)致的，進(jìn)入回轉(zhuǎn)運(yùn)動(dòng)以后會(huì)維持在平均30%的降速范圍內(nèi)。而對(duì)于艏搖速率來說，初始的明顯速率變化是由于受到轉(zhuǎn)舵的影響，而后期的波動(dòng)則是由于船舶遭遇變化的浪向?qū)е拢畲蟮聂紦u速率可達(dá)12.2（°）/s。

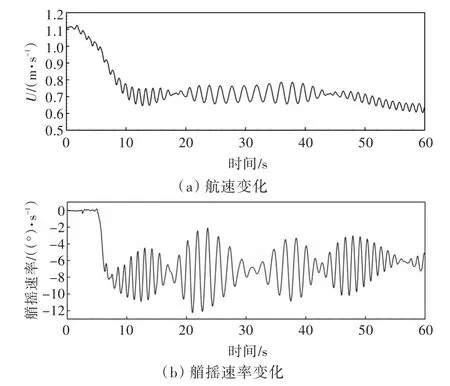
圖10 波浪中自由回轉(zhuǎn)操縱中船舶航速和首搖速率時(shí)歷曲線Fig.10 Time history curves of ship speed and yaw rate for turning circle maneuvering in waves

圖11所示為船舶在波浪中進(jìn)行自由回轉(zhuǎn)操縱運(yùn)動(dòng)過程中螺旋槳推力和扭矩的變化曲線。從圖中可以看出，螺旋槳的推力和扭矩呈現(xiàn)出明顯的波頻振動(dòng)特性，這主要是由于船舶運(yùn)動(dòng)過程中導(dǎo)致螺旋槳的進(jìn)流產(chǎn)生變化，進(jìn)而使得推進(jìn)性能產(chǎn)生波動(dòng)。從局部放大圖中可以看到更為高頻的振蕩現(xiàn)象，這是由于真實(shí)旋轉(zhuǎn)螺旋槳葉片切割流場(chǎng)導(dǎo)致。

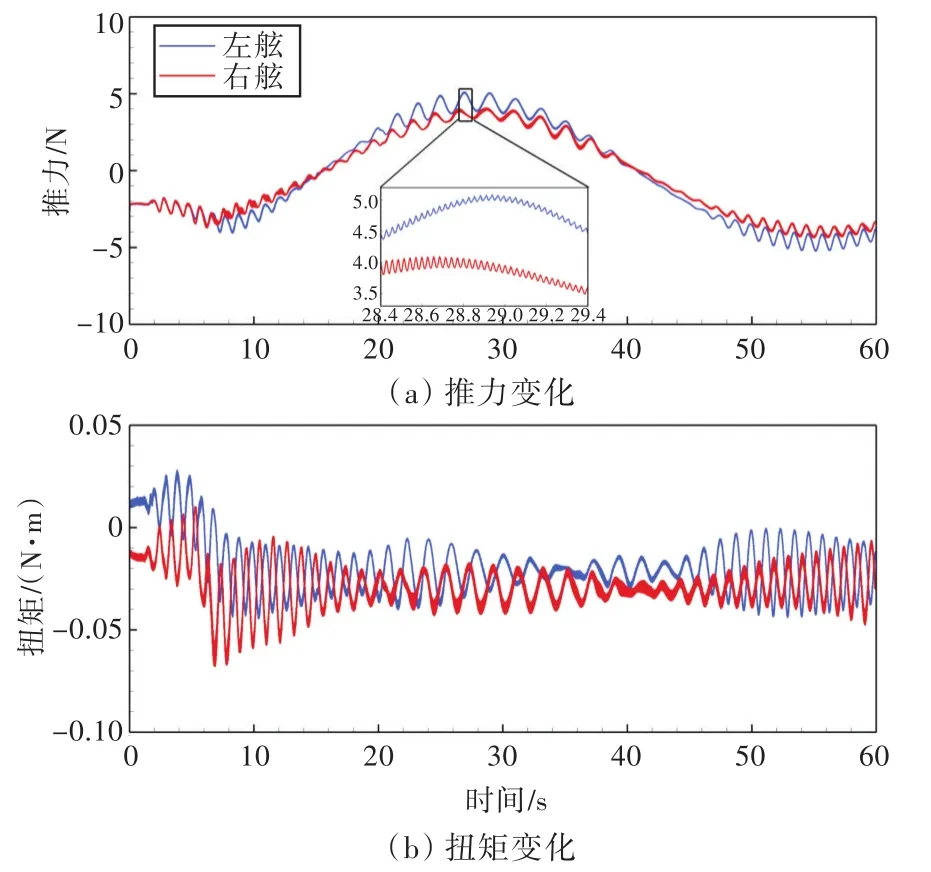
圖11 波浪中自由回轉(zhuǎn)操縱中船舶推進(jìn)性能時(shí)歷曲線Fig.11 Time history curves of propulsion coefficients for turning circle maneuvering in waves

圖12所示為轉(zhuǎn)舵時(shí)刻舵所受到的水動(dòng)力載荷的變化曲線。從圖中可以看出，執(zhí)行轉(zhuǎn)舵操作之前，作用在兩側(cè)舵上的阻力基本一致，并且側(cè)向力對(duì)稱，而執(zhí)行完操舵以后，舵阻力增加明顯，而側(cè)向力變成同向，產(chǎn)生較大的側(cè)向合力，而側(cè)向力的合力也使得船舶產(chǎn)生回轉(zhuǎn)運(yùn)動(dòng)。

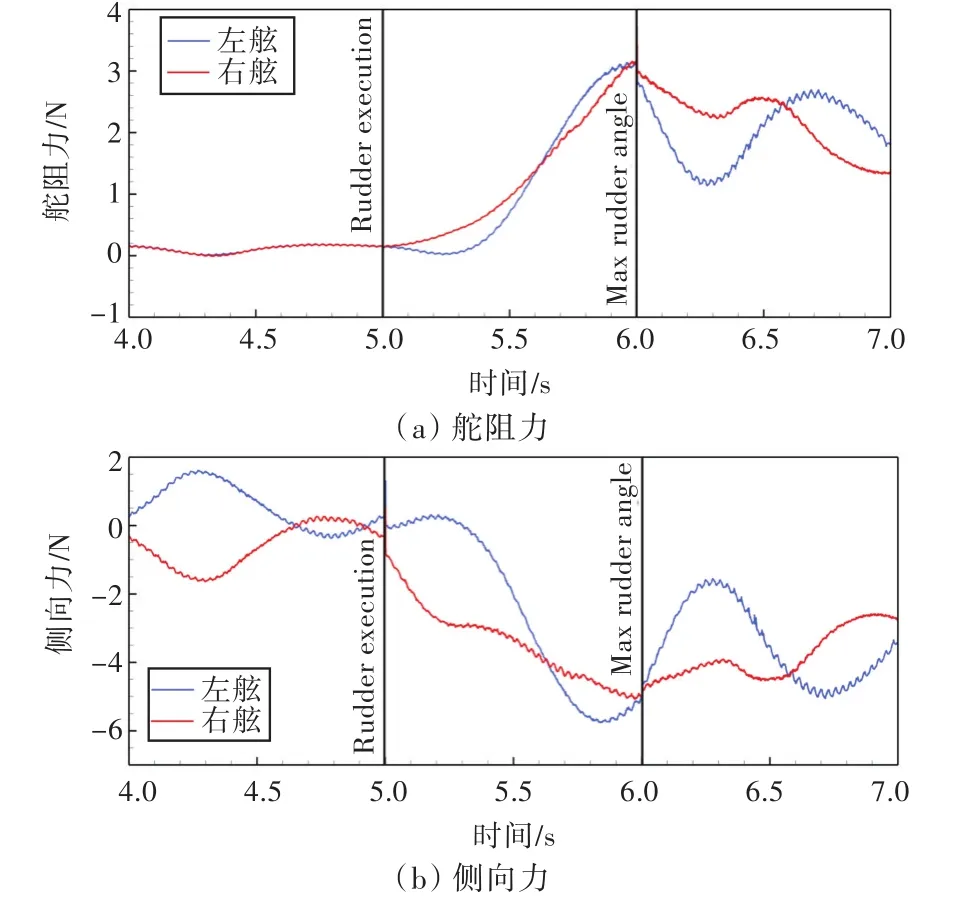
圖12 轉(zhuǎn)舵過程中舵受到的水動(dòng)力時(shí)歷曲線Fig.12 Time history curves of rudder forces during rudder execution

圖13所示為在轉(zhuǎn)舵過程中的槳舵周圍的渦量場(chǎng)變化。從圖可以看出，初始時(shí)刻，舵角為0°時(shí)，槳舵周圍的渦量分布基本為對(duì)稱形式，而隨著舵角的增加，舵對(duì)前面螺旋槳的瀉渦會(huì)產(chǎn)生明顯的干擾，由于舵向左舷轉(zhuǎn)動(dòng)，因此左舷舵會(huì)對(duì)螺旋槳的槳轂渦產(chǎn)生干擾，而右舷舵則會(huì)影響到右舷槳的葉梢渦。這種現(xiàn)象的區(qū)別也解釋了圖11和圖12中兩側(cè)螺旋槳和舵水動(dòng)力的區(qū)別。而舵周圍會(huì)發(fā)生明顯的流動(dòng)分離現(xiàn)象，但是現(xiàn)在采用的是RANS方法，無法精確地捕捉這種情況下的周圍流動(dòng)，因此會(huì)對(duì)舵力的計(jì)算產(chǎn)生誤差，這也是導(dǎo)致目前計(jì)算中的回轉(zhuǎn)圈變大的原因之一。

圖13 轉(zhuǎn)舵過程中槳舵周圍的渦量場(chǎng)Fig.13 Snapshots of vortical field around twin propellers and rudders during rudder execution

圖14所示為船舶在波浪中自由回轉(zhuǎn)過程中，4個(gè)典型時(shí)刻的自由面波形變化，分別對(duì)應(yīng)于0°、120°、240°和 360°航向角的時(shí)刻。從圖中可以看出，在沒有轉(zhuǎn)向時(shí)，船舶周圍的波浪環(huán)境基本對(duì)稱，但是在回轉(zhuǎn)角度達(dá)到360°時(shí)，船艏和船艉處均能看出由于轉(zhuǎn)動(dòng)導(dǎo)致的兩側(cè)波面的差別；而從120°和240°航向角時(shí)的自由面可以看出，兩側(cè)波面存在明顯的高度差別，這也導(dǎo)致了船體兩側(cè)的壓力分布不均；從圖14（d）同樣可以看出船艏會(huì)抬出水面，這證明了在該波浪情況下船舶會(huì)產(chǎn)生大幅度的六自由度運(yùn)動(dòng)。

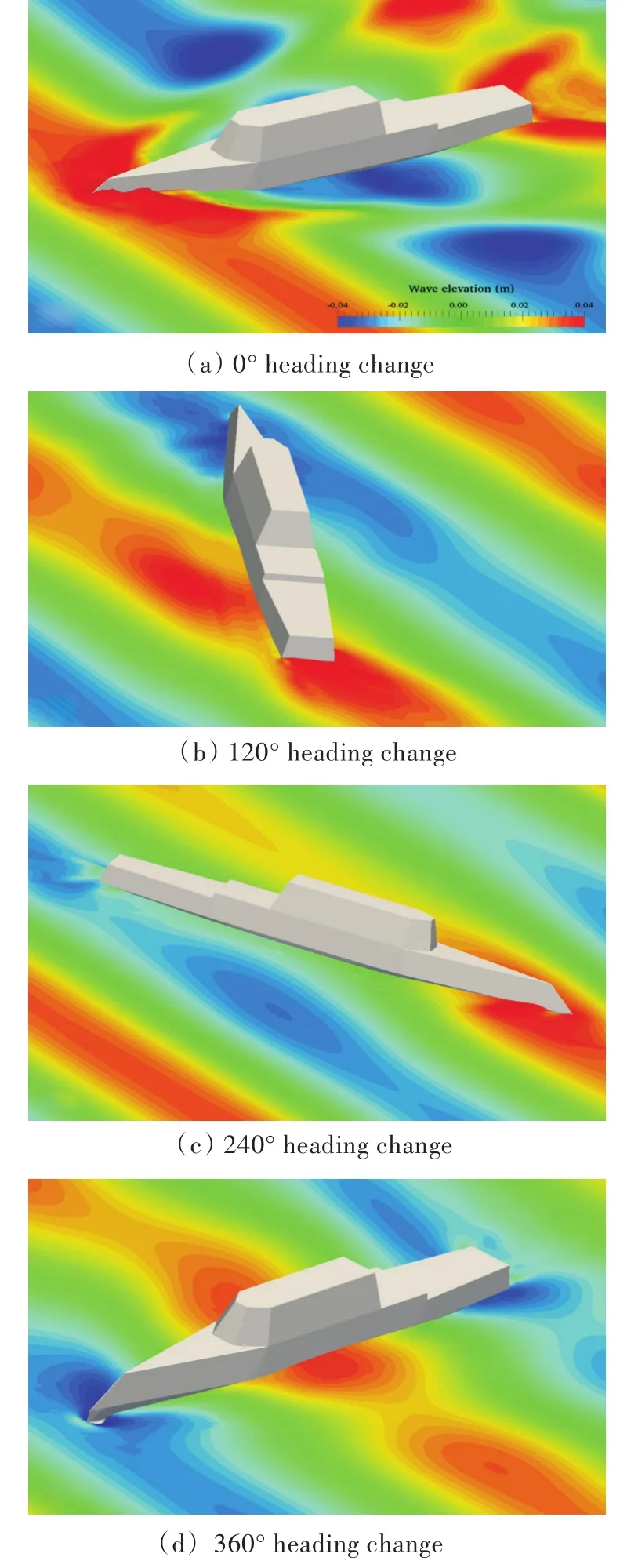
圖14 波浪中自由回轉(zhuǎn)過程中船舶周圍自由面Fig.14 Snapshots of wave elevation around ship hull for turning circle maneuvering in waves

4 結(jié) 語(yǔ)

本文采用結(jié)合重疊網(wǎng)格技術(shù)的CFD求解器naoe-FOAM-SJTU，對(duì)船—槳—舵相互作用下的波浪中船舶自由回轉(zhuǎn)操縱運(yùn)動(dòng)進(jìn)行了直接數(shù)值模擬。數(shù)值預(yù)報(bào)的波浪中船舶回轉(zhuǎn)運(yùn)動(dòng)的回轉(zhuǎn)圈特征參數(shù)（如縱距、橫距、戰(zhàn)術(shù)直徑、回轉(zhuǎn)直徑等）與已有試驗(yàn)結(jié)果吻合較好，誤差均在10%以內(nèi)，驗(yàn)證了當(dāng)前求解器對(duì)船—槳—舵相互作用下的波浪中船舶自由回轉(zhuǎn)操縱運(yùn)動(dòng)預(yù)報(bào)的適用性和可靠性。此外，根據(jù)計(jì)算結(jié)果顯示，船舶的垂蕩、縱搖和橫搖運(yùn)動(dòng)展現(xiàn)出明顯的波頻運(yùn)動(dòng)響應(yīng)，而縱蕩、橫蕩和艏搖3個(gè)平面運(yùn)動(dòng)的波頻振動(dòng)特征不明顯。在波浪中船舶進(jìn)行自由回轉(zhuǎn)時(shí)的最大船舶失速可達(dá)40%。同時(shí)，給出了整個(gè)操縱運(yùn)動(dòng)過程中的推進(jìn)性能和舵力的變化。并且通過詳細(xì)的流場(chǎng)信息，如不同時(shí)刻自由面變化和槳、舵周圍渦量場(chǎng)變化等，分析了波浪中回轉(zhuǎn)操縱運(yùn)動(dòng)下水動(dòng)力變化的原因。

由于當(dāng)前數(shù)值模擬采用時(shí)均的RANS方法進(jìn)行流場(chǎng)求解，因此對(duì)于槳、舵周圍大分離流動(dòng)現(xiàn)象捕捉的精度較差，這也導(dǎo)致了目前的數(shù)值預(yù)報(bào)存在一定的誤差，將來的工作將主要開展基于更為精確的分離渦模擬方法進(jìn)行該問題的求解，以給出更精細(xì)的流場(chǎng)模擬，獲取更高精度的數(shù)值預(yù)報(bào)結(jié)果。